基于核主成分分析和食肉植物算法优化随机森林的风电功率短期预测

陈晓华，吴杰康，龙泳丞，王志平，蔡锦健

（1.广东电网有限责任公司湛江供电局，广东 湛江 524005；2.广东工业大学自动化学院，广东 广州 510006；3.东莞理工学院电子工程与智能化学院，广东 东莞 523808）

0 引言

风力发电作为低成本、可再生的清洁能源受到了广泛的重视，越来越多风力发电设备接入电网中［1］。风力发电能在一定程度上缓解能源危机，但由于风电功率受气象因素影响较大，所以风电功率具有随机性和间歇性等特点，进而给风电功率的准确预测带来技术上的难度。风电功率短期预测一般指对未来3 天之内的风电输出功率进行预测，高精度的短期预测有助于促进风电的利用以及电网的安全稳定运行［2］。

目前对于风电功率短期预测的研究方法主要包括物理方法和基于数据驱动的预测方法。物理方法主要通过利用数值天气预报数据等信息，建立复杂的数学模型并对其求解得出预测结果，但该方法计算复杂且精度不高，不适用于风电功率短期预测［3］。基于数据驱动的预测方法主要通过利用机器学习或深度学习方法对风速、风向、温度和海拔高度等数据进行训练和回归预测，进而实现风电功率的短期预测。常见的机器学习方法有支持向量机［4］、梯度提升树［5］、邻域KNN 算法［6］和随机森林（random forest，RF）［7］等。常见的深度学习方法有卷积神经网络［8］、深度置信网络［9］、双向门控循环单元网络［10］、Elman网络［11］、长短期记忆网络（long short-term memory，LSTM）［12］、门控循环单元网络［13］、生成对抗网络［14］和极限学习机［15］等，利用深度学习方法可以获得一定的预测效果，但需要大量样本数据并且消耗的时间比较长，不适用于风电功率短期预测。李国全等人利用改进乌鸦搜索算法优化支持向量机参数获得精度更高的预测模型［4］，但改进的算法会增加运算时间。孙川永等人利用数值天气预报和梯度提升树算法相结合的方法对风电功率进行短期预测，获得满意的效果［5］，但梯度提升树需要调参，人为随机设置的参数有时会导致预测效果不理想。RF 在处理非线性的风电功率数据方面具有明显的优势，可以快速获得较好的预测效果，然而RF 和支持向量机一样，超参数设置不同的数值会影响预测效果。因此，采用寻优精度高、收敛速度快的食肉植物算法（carnivorous plant algorithm，CPA）优化RF 建立风电功率短期预测模型可以克服RF 预测模型预测精度不够高的问题。

针对以往研究的不足，提出一种基于核主成分分析和CPA 优化RF 的风电功率短期预测方法。利用核主成分分析选出8 个气象因素作为预测模型的输入，然后，通过CPA 优化RF 构建CPA-RF 预测模型克服RF 预测模型预测效果比较差的缺点。

1 基于核主成分分析的特征提取

与主成分分析方法相比，核主成分分析利用核函数把非线性的样本数据映射到高维空间中，并在高维空间对样本数据进行线性处理，该方法可以有效解决主成分分析方法只能处理线性数据等问题，并且方差贡献率更加集中，样本数据降维效果更好。由于论文篇幅有限，核主成成分分析的数学原理不再赘述，具体推导可参考文献［16-17］。

核主成分分析算法的具体步骤如下［16-17］：

1）输入样本数据，并在MATLAB 中调用zscore函数对数据进行标准化处理，消除数据不同量纲的影响；

2）设置径向基参数为2.5，并利用径向基核函数计算核矩阵G；

3）对核矩阵G进行中心化处理，可得矩阵G′；

4）求出矩阵G′的特征值和特征向量；

5）对矩阵G′的特征值进行降序排列，并找出对应顺序的特征向量；

6）计算核主成分的数值、方差贡献率和累计贡献率。

2 CPA-RF风电功率短期预测模型

2.1 CPA

CPA 通过模拟食肉植物的吸引、捕获、消化以及繁殖的过程来达到寻优的目的［18］。CPA 的数学模型如下所示：

1）初始化阶段。

按照式（1）对CPA 的种群个体进行初始化。

式中：xi,j为第i个个体在第j维度上的位置；i=1,2,…,N，N为Nplant棵食肉植物和Nprey个猎物个体的和，即N=Nplant+Nprey；j=1,2,…,d，d为待求解优化问题的维数；μj、分别为第j维变量的下限和上限；ηi,j为第i行第j列上产生的随机数，取值范围为［0，1］。

对食肉植物算法的种群个体进行初始化后可得种群的初始位置为

对于第i个个体，也就是式（2）的第i行所有变量，它代表优化问题的一个可行解。

为了确定可行解是否是最优的，需要将第i个个体代入适应度函数f(·)中求解适应度函数值来判断，将结果存储到矩阵中，可得

对于最小化问题来说，适应度函数值越小，则该可行解越接近最优解。

2）分类与分组阶段。

算法的分类过程为：将式（3）计算得到的适应度函数值从小到大进行排序，把前面Nplant个个体作为食肉植物，剩下的Nprey个个体作为猎物。

算法的分组过程为：把Nplant棵食肉植物和Nprey个猎物分别从小到大依次排序，并将第1 个猎物分配给第1 棵食肉植物，将第2 个猎物分配给第2 棵食肉植物，以此类推，将第Nplant个猎物分配给第Nplant棵食肉植物。由于算法中猎物的个数大于食肉植物的数量，所以将第Nplant+1 个猎物分配给第1 棵食肉植物，依次类推，直到第Nprey个猎物分配给第Nplant棵食肉植物为止，并且满足关系式k=Nprey/Nplant≥2。算法的分组过程如图1 所示。

图1 CPA分组过程Fig.1 Grouping process of carnivorous plant algorithm

3）生长阶段。

由于土壤的营养成分不足，食肉植物会通过吸引、捕获和消化猎物的方式来获得营养，从而促进自身的生长。食肉植物会散发香味吸引猎物，但猎物也有可能从逃脱食肉植物的魔爪。因此，在算法中引入吸引率，在图1 中，每一棵食肉植物都随机选取一个猎物，若吸引率大于随机产生的一个数字，则食肉植物会被捕到该猎物并且消化它，进而促进食肉植物的生长。此时，食肉植物的生长数学模型为：

式 中：xi′,j为在第j维度上的第i′ 棵食肉植物，i′=1,2,…,Nplant；为生长率预设的数值；为用随机数更新后的生长率；为在第j维度上对应食肉植物的那一组随机选择的第v个猎物；ηi′,j为第i′行第j列上产生的随机数，取值范围为［0，1］。

若吸引率小于随机产生的一个数字，则猎物可以逃脱食肉植物的魔爪并且继续生长。此时，对应该行为的数学模型为：

食肉植物和猎物的生长过程一直在不断地重复，直到达到预设的生长迭代次数Tgrowth为止。

4）繁殖阶段。

食肉植物通过消耗猎物进行繁殖，并且算法中只允许第1 棵食肉植物可以繁殖。食肉植物繁殖过程的数学模型为：

式中：i′ ≠v′ ≠1；x1,j为算法的最优解；为繁殖率；xv′,j为在第j维度上的第v′棵食肉植物；为计算参数。

在繁殖的过程中，无论维度如何，都会重新选择第v′棵食肉植物，并且该过程会重复Nplant次。

5）更新适应度和组合阶段。

将新生成的所有食肉植物以及猎物个体均添加到初始的种群中，并计算所有个体的适应度函数值，按从小到大的顺序重新排序，把排在前N名的个体作为进入新的初始种群并进行下一轮的迭代更新。

6）算法的终止阶段。

重复步骤2）—步骤5），直到满足最大迭代次数Tmax为止。

2.2 RF回归

RF 可以看作是由多棵彼此之间无关联、相互独立的决策树组成的一种算法，该算法首先采用Bootstrap 采样方法，从原始的样本数据中提取多个样本，根据每一个Bootstrap 样本数据建立对应的决策树模型，然后对多棵决策树的预测结果进行相加并求取平均值，最后可得出RF 的预测效果［19］。

RF 回归模型采用均方误差最小的原则对样本数据进行划分，在抽样样本数据对应的节点处划分为两个样本数据集并分别计算它们的均方误差，将两个样本数据集各自均方误差最小且两个样本数据集的均方误差之和最小的点作为分裂节点。

在RF 算法中，设置不同决策树的数量ntree和分裂节点处特征变量的数量mtry会对预测结果产生较大的影响。因此，选择利用食肉植物算法对RF 算法中的ntree和mtry这两个参数进行优化，从而获得预测性能更好的CPA-RF 预测模型。

2.3 构建CPA-RF的风电功率短期预测模型

构建CPA-RF 风电功率短期预测模型步骤如下：

1）对采集到与风电功率有关的多个影响因子进行核主成分分析，将贡献率较高的几个影响因子作为预测模型的输入。

2）对贡献率较高的几个影响因子和风电功率数据的训练集和测试集的比例设置为7∶3，将贡献率较高的几个影响因子和训练集数据归一化后一起训练CPA-RF 预测模型，其中归一化的计算表达式为［20-23］

式中：H为原始数据；Hmin为原始数据最小值；Hmax为原始数据最大值。

3）设置食肉植物算法种群数量N=40，其中食肉植物的棵数Nplant=10，猎物个体的数量Nprey=30；最大迭代次数Tmax=20；待求解优化问题的维数d=2；搜索空间变量的下限μ1=μ2=0.1 和上限；生长率；吸引率为0.8；生长迭代次数Tgrowth=2；繁殖率

4）初始化种群个体。

5）以平均绝对百分比误差作为种群个体的适应度函数，计算表达式为

式中：Treal(t) 为t时刻实际的风力发电功率；Tpred(t)为t时刻预测的风力发电功率；h为训练集样本数。

6）将食肉植物和猎物进行分类和分组。

7）判断吸引率是否大于随机数。如果条件成立，食肉植物将会成长；否则，猎物会挣脱并成长。

8）第一棵食肉植物进行繁殖。

9）更新适应度并组合新种群。

10）判断算法是否已达到最大迭代次数，如果是，那么停止迭代，输出RF 的最优参数，得到CPARF 预测模型；否则，返回步骤5），直到满足终止条件为止。

将贡献率较高的几个影响因子和测试集数据归一化后一起输入到训练好的CPA-RF 预测模型中，从而获得风电功率的预测结果。

基于核主成分分析和食肉植物算法优化RF 的风电功率预测流程如图2 所示。

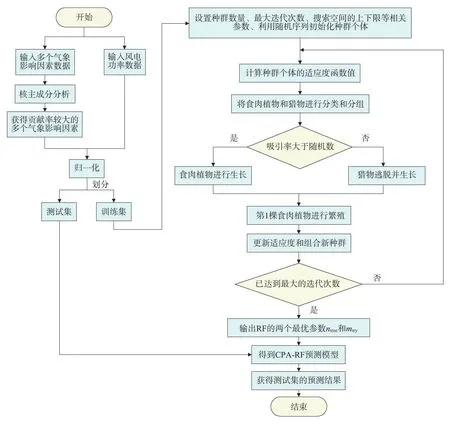
图2 基于核主成分分析和食肉植物算法优化RF的风电功率预测流程Fig.2 Wind power prediction flow chart based on random forest optimized by kernel principal component analysis and carnivorous plant algorithm

3 仿真分析

对某地风力发电功率进行短期预测，选取某地区2019 年1 月1 日—12 日的13 个气象因素以及风电功率数据进行研究。这13 个气象因素包括测风塔10 m 风速、测风塔30 m 风速、测风塔50 m 风速、测风塔70 m 风速、轮毂高度风速、测风塔10 m 风向、测风塔30 m 风向、测风塔50 m 风向、测风塔70 m风向、轮毂高度风向、温度、气压、湿度。选取1 月前10 天的气象数据和风电功率数据作为训练集，其中1 月前10 天的风力发电功率历史数据如图3 所示，所选取的风电功率数据的每次采样时间为15 min，一共采样960 个数据点。选取1 月11 日和12 日的气象数据和风电功率数据作为测试集，即选取1 月11 日和12 日作为待预测日期，其中预测时间间隔为15 min，一共输出192 个风力发电功率预测数据。

图3 1月前12天的风力发电功率Fig.3 Wind power in the first 12 days of January

3.1 选出合适的气象因素

风电功率受风向、风速、温度、气压和湿度等影响。若将所有的气象因素都输入到预测模型中，则会增加预测模型的训练难度和时间。由于这13 个气象因素和风电功率之间呈现非线性关系，因此，相比较于主成分分析算法，采用核主成分分析算法提取出与风电功率有着很强相关性的气象因素具有明显的优势。基于核主成分分析的方差贡献率和累计贡献率如图4 所示。

图4 基于核主成分分析的方差贡献率和累计贡献率Fig.4 Variance contribution rate and cumulative contribution rate based on kernel principal component analysis

由图4 可知，前8 个主成分的累计贡献率达到99.98%，说明这8 个气象因素与风力发电功率的输出有着很大的关系。因此，选择这8 个气象因素作为预测模型的输入变量。

3.2 风电功率预测仿真结果及其分析

为了突出利用核主成分分析方法提取前8 个与风力发电功率有关气象因素的合理性和有效性，分别选择前8 个气象因素和13 个气象因素作为输入变量，对1 月11 日和12 日的风电功率进行预测，基于LSTM 预测模型、双向长短期记忆神经网络（bidirectional long short-term memory，BiLSTM）预测模型、RF 预测模型和CPA-RF 预测模型的仿真结果如图5 所示。

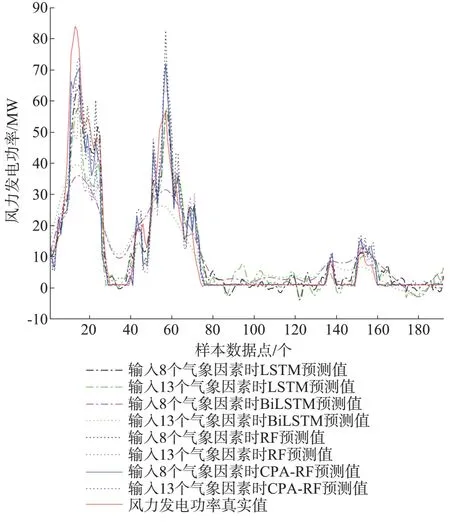
图5 4种预测模型预测效果的对比Fig.5 Comparison of prediction effect of four prediction models

从图5 中可以看出，LSTM 预测模型和BiLSTM预测模型的预测值均会出现负数的情况，这显然不符合实际情况，而RF 预测模型和CPA-RF 预测模型的预测值都没有出现负数的情况，证明此时使用RF预测模型和CPA-RF 预测模型对风电功率进行短期预测的准确性和合理性。并且从图中可以看出，当输入8 个气象因素时，基于CPA-RF 预测模型的预测值最接近于风力发电功率真实值，证明利用核主成分分析方法提取8 个气象因素作为输入要比单纯直接输入13 个气象因素的效果要好，多余的5 个气象因素会影响到预测模型的预测精度。

3.3 风电功率预测模型结果的评价指标

采用均方根误差TRMSE、平均绝对误差TMAE以及绝对误差TAE这3 种误差指标对1 月11 日和12 日的风电功率预测结果进行评价，计算表达式分别为［23-24］：

式中：m为预测样本数据的数量。

1）均方根误差和平均绝对误差的比较。

分别输入8 个气象因素和13 个气象因素时，基于LSTM 预测模型、BiLSTM 预测模型、RF 预测模型和CPA-RF 预测模型的均方根误差和平均绝对误差的结果分别如表1 和表2 所示。

表1 输8个气象因素时不同方法预测误差分析Table 1 Prediction error analysis of different methods when inputting 8 meteorological factors 单位：MW

表2 输入13个气象因素时不同方法预测误差分析Table 2 Prediction error analysis of different methods when inputting 13 meteorological factors 单位：MW

从表1 和表2 中可以看出，对于同一种预测方法，当分别输入8 个气象因素和13 个气象因素时，除了BiLSTM 预测模型的均方根误差和平均绝对误差一样之外，其余的预测方法都是输入8 个气象因素的预测效果要比输入13 个气象因素好，证明利用核主成分分析方法提取8 个气象因素作为输入的有效性，比直接输入13 个气象因素更加合理和可靠。另外，当输入8 个气象因素时，基于CPA-RF 预测模型的均方根误差和平均绝对误差是所有预测方法中最小的，证明把核主成分分析和利用食肉植物算法优化RF 这两种方法相结合可以提高预测模型的预测精度。

2）绝对误差的比较。

绝对误差可以描述单个预测值与实际风电功率数值之间差异的大小。分别输入8 个气象因素和13个气象因素时，基于LSTM 预测模型、BiLSTM 预测模型、RF 预测模型和CPA-RF 预测模型的绝对误差如图6 所示。

从图6 中可以看出，在所有预测方法中，当输入8 个气象因素时，基于CPA-RF 预测模型的绝对误差在大部分样本数据点是最小的，进一步证明结合核主成分分析方法和CPA-RF 预测模型对风力发电功率进行预测的可靠性和准确性，其预测结果更准确，有助于解决风电功率短期预测精度不够高的问题。

3）4 种预测模型耗时的比较。

分别输入8 个气象因素和13 个气象因素时，基于LSTM 预测模型、BiLSTM 预测模型、RF 预测模型和CPA-RF 预测模型的耗时结果如表3 所示。

表3 不同预测方法的耗时Table 3 Time consuming for different prediction methods 单位：s

从表3 种可以看出，对于同一种预测方法，输入13 个气象因素的耗时均比输入8 个气象因素要长，这是因为输入气象因素比较多从而导致预测模型耗时长。另外，当输入8 个气象因素时，LSTM 预测模型和BiLSTM 预测模型的耗时均达到70 s 以上，而RF 预测模型的耗时只有5.893 s，CPA-RF 预测模型的耗时为12.811 s，证明使用LSTM 预测模型和BiLSTM 预测模型的耗时远远多于RF 预测模型，而CPA-RF 预测模型的耗时仅比RF 预测模型多6.918 s。

综合预测精度和耗时这两个方面，CPA-RF 预测模型是最好的选择。

4 结论

针对风电功率短期预测精度不够高的问题，提出一种基于核主成分分析和CPA-RF 的风电功率短期预测方法，并选取某地区在2019 年1 月1 日—12日的数据进行研究，可以得出以下结论：

1）若选取13 个气象因素作为风电功率短期预测的输入，结果往往不够准确。而利用核主成分分析选出8 个重要气象因素作为预测模型的输入可以很好地解决输入全部气象因素所造成的精度不高问题，验证了核主成分分析方法选出主成分的合理性和准确性。

2）利用食肉植物算法优化RF 中决策树的数量和分裂节点处特征变量的数量可以获得比RF 预测精度更高的CPA-RF 预测模型，证明方法的可行性，为提升风电功率短期预测精度提供思路。

3）LSTM 预测模型和BiLSTM 预测模型的耗时比RF 预测模型和CPA-RF 预测模型都要多得多，并且预测数值出现了负数情况，不符合实际。而在输入8 个气象因素时，CPA-RF 预测模型仅比RF 预测模型多6.918s，但预测精度有所提升。因此，在兼顾用时和预测精度这两个方面，CPA-RF 预测模型是最优的选择。