基于超声多尺度衰减的螺栓轴向应力评价

余 鑫, 陈 平, 胡义亮, 付 统, 李长泽

(重庆大学 机械与运载工程学院,重庆 400044)

螺栓联接广泛应用于桥梁、建筑物、机械和车辆等领域。为螺栓提供适当的预载,保证螺栓连接的安全性和稳定性至关重要。预载不足将导致连接部件产生相对滑动,过载将导致螺栓强度失效或结构部件局部损坏,从而造成设备损坏、产品不合格,甚至引发严重的安全事故[1]。因此,在设备服役期间,对螺栓受力状态进行有效监测,对于保持螺栓的可靠性和降低结构或机器故障的风险至关重要,这一点受到广泛关注[2]。目前,常用的应力测量方法包括电阻应变计法[3]、扭矩扳手法[4]和超声波测量法[5-8]等。应变计法受到测量空间条件的限制,使得在螺栓表面安装应变计变得困难。扭矩扳手法由于螺纹和螺母接触表面间以及螺栓头部与工件的摩擦因数的影响,只有约10%-15%的扭矩可转化为轴向载荷。而超声波测量法具有精度高、稳定性好、适应性强等优点,是目前应用广泛且成熟的一种无损检测方法,是未来螺栓轴向应力测量的主要发展方向。

常规的超声波测量法以声弹性原理为基础,即固体结构在静应力状态下的相速度随应力大小发生变化[9-10]。在实际操作中,由于声波速度难以直接获取,一般以声波在固体中的渡越时间作为测量指标。一方面,声弹性效应非常微弱,其造成的渡越时间增量也非常小;另一方面,对于短螺栓,在相同应力下,轴向伸长量较小,使螺栓负载前后的渡越时间差异难以区分,导致获取到的渡越时间的准确度大大降低。因此,渡越时间法对短螺栓轴向应力的评估并不适用。

近年来有学者研究发现,在受载固体中的超声波衰减系数与应力之间存在一定的联系。Turner等[11]为基于超声散射衰减的多晶微结构应力值提取提供了理论基础。后来被Kube等[12-13]推广,提出了与柯西应力相关的等效弹性常数。Kube等[14]以上述研究和Weaver[15]的散射衰减系数模型为基础,提出了包含应力影响的散射衰减系数。以上研究表明,超声散射衰减系数对螺栓规格、安装条件等因素并不敏感,其主要依赖于结构内部各向异性,并对应力变化更加敏感。然而,超声回波信号是一种非稳定信号,其中包含了与轴向应力无关的信号成分,且容易受到噪声等杂波信号的干扰。因此,传统衰减法不能在局部时间范围内提供更丰富的轴向应力信息,进而影响轴向应力测量精度。本文基于超声散射衰减理论以及小波多尺度分解,提出了一种超声多尺度衰减的螺栓轴向应力测量方法,有效滤除掉与轴向应力无关的信号成分。并结合灰色关联分析和粒子群优化算法,抑制了测量模型拟合本身带来的误差。试验结果表明,相对于传统衰减法,该方法能够有效提高螺栓轴向应力的测量精度,具有一定的技术实用价值。

1 理论模型

1.1 受载杆状金属的散射衰减系数

超声波在金属杆状类零件的传播过程中会产生能量耗损,这种能量的耗损称为超声衰减。其按原理可分为吸收衰减、耗散衰减和散射衰减。金属杆内超声波沿轴向方向的传播示意图,如图1所示。由于介质不具有黏弹特性和杆边界的反射效应等因素,使得吸收衰减和耗散衰减相对于散射衰减可忽略不计。因此,超声在螺栓等杆类零件的衰减基本上由散射产生。

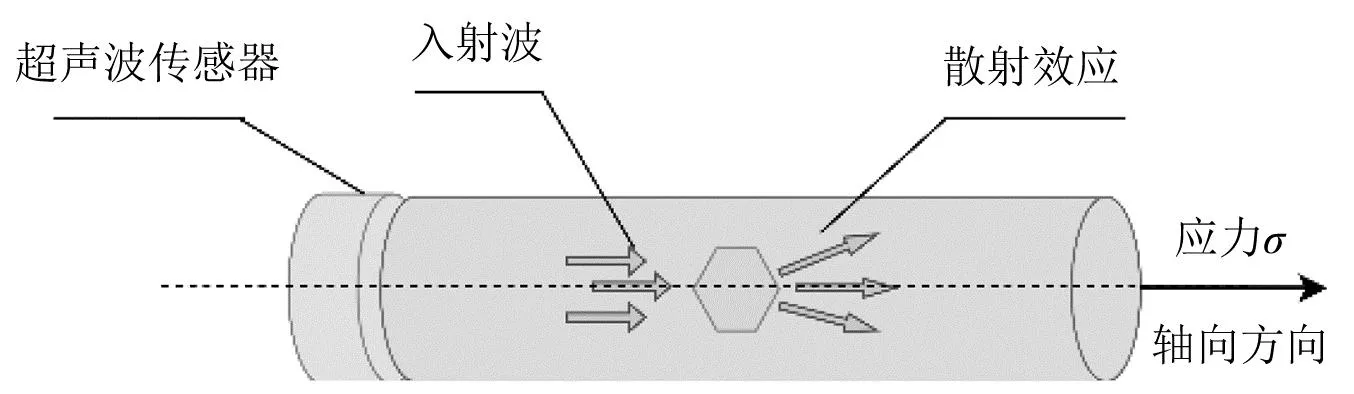
图1 超声波在杆状金属内的散射效应Fig.1 Scattering effect of ultrasonic waves in rod-shaped metal

当弹性波在无织构多晶体介质中传播时,介质的应力状态会影响弹性波的相速度和介质内部的散射衰减系数。纵波衰减系数与介质应力的关系可近似表示为

(1)

式中:ω为中心频率;l为介质晶粒平均直径;VL和VS分别为纵波和横波的相速度;v为二阶各向异性常数;ζ为民综合各向异性常数;σ为轴向应力的幅值。此时(ωl)4/V2≪1,即属于瑞利散射区。式(1)表明,衰减系数与应力呈二次递增关系。

螺栓的详细参数示意图,如图2所示。螺栓的有效受力长度包括螺栓杆的夹紧部分以及螺栓头和螺母的一部分。根据文献[16],螺栓等效受力长度内所受到的应力可看作均匀分布的。则整个螺栓的均匀化衰减系数可表示为

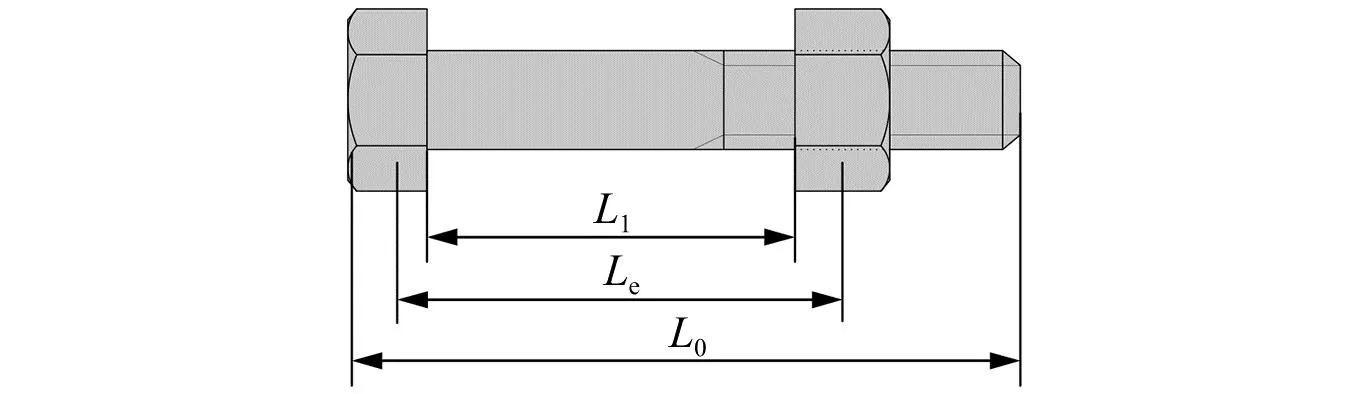
图2 螺栓的尺寸参数示意图Fig.2 Schematic diagram of the size parameters of the bolt

(2)

式中:Le为有效受力长度;L0为螺栓全长;α(σ)为受均匀化应力σ轴段的衰减系数;α(0)为零应力轴段的衰减系数,由于螺栓的有效应力长度不易精确获得,因此在工程应用中通常使用经验公式[17]

(3)

式中:L1为螺母和螺栓头之间的实际夹紧距离;Dt和Dr分别为螺栓杆螺纹部分等效直径和无螺纹螺栓杆直径。将式(2)代入式(1)得

αL(σ)=ALLeσ2+BLLeσ+CL

(4)

其中

(5)

(6)

(7)

式 (4) 表明,螺栓加载前后其纵波衰减值与轴向应力呈二次函数关系。由于AL≪BL,所以式 (4) 中的二次项系数可以忽略不计,最终得出应力与纵波衰减的关系为

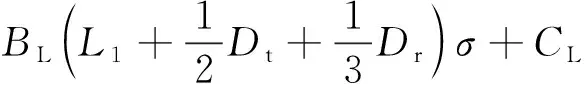
(8)

根据式(8),当夹紧长度一定时,轴向应力与纵波衰减值呈线性关系。

1.2 多尺度衰减模型

假设螺栓在超声波传播方向上晶粒取向独立且弹性性质随机分布,利用脉冲反射法采集受载螺栓的超声波信号f(t),由于无需考虑信号频率泄露造成的影响,因此利用矩形窗函数截取f(t)中的第一次底面回波信号f1(t)和第二次底面回波信号f2(t),传统衰减模型的衰减系数可定义为[18]

(9)

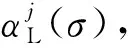
(10)

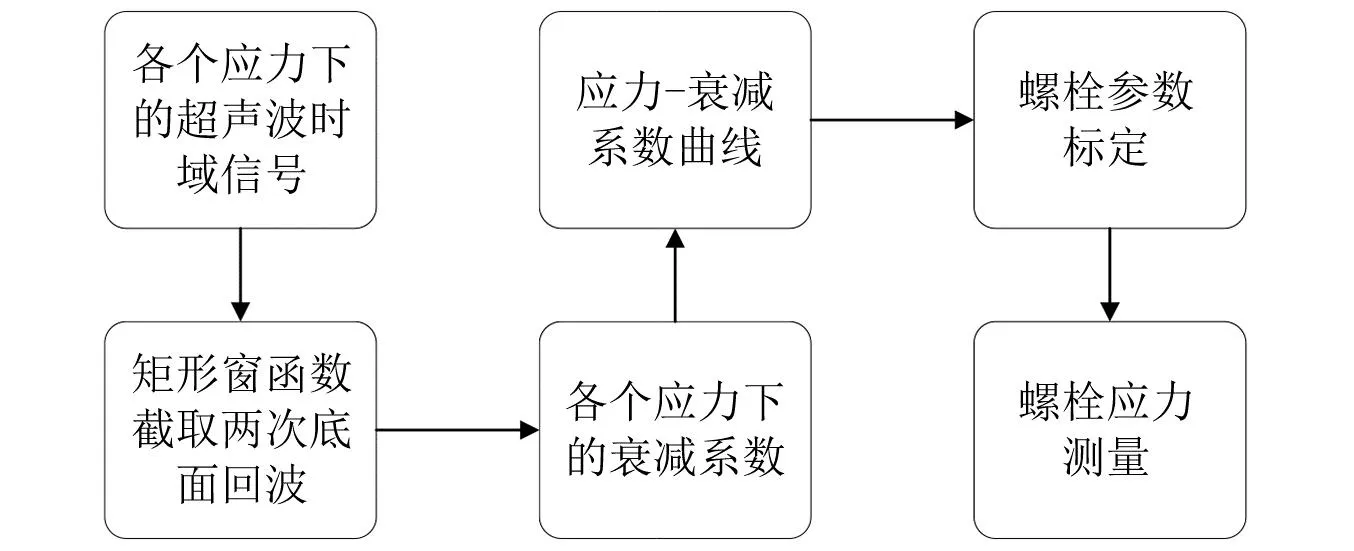
图3 传统衰减法螺栓应力测量流程图Fig.3 Flow chart of stress measurement by conventional attenuation method

选定ψ(t)为任一小波母函数,对f1(t)与f2(t)进行连续小波变换,分别求得螺栓一次底面回波和二次底面回波的小波系数矩阵F1(a,b)和F2(a,b)

(11)

(12)

式中:a为尺度变量;b为平移变量;ψa,b(t)为小波函数族,将连续的正整数a分解为M层;小波系数矩阵中第i行(i=1,2,…,M)为原始信号在尺度为ai时的小波分量。螺栓在尺度ai下的衰减系数定义为

(13)

(14)

本文通过粒子群优化算法与灰色关联分析相结合的方法,得到各个尺度衰减系数的最优权重分配,具体方法如下:

(1) 超声波信号经过小波变换共分解为M个尺度,假设所有尺度均为代表性尺度。

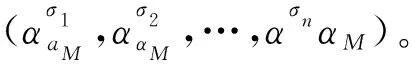
式中:X为系统行为特征序列;Y为相关因素序列的情形。定义灰色关联系数

γ[x(k),yi(k)]=

(15)

以及Yi(i=1,2,…,M)与X的灰色关联度[19]

(16)

式中,ξ为分辨率。根据各个尺度的衰减系数与螺栓轴向应力的关联度从高到低的次序选择m个尺度作为代表性尺度。

(3) 若初始化粒子总数为Q,则粒子速度和位置的更新函数分别为[20]

vq(t+1)=Ωvq(t)+c1r1(pbest-Wq)+
c2r2(gbest-Wg)

(17)

Wq(t+1)=Wg(t)+vq(t+1)

(18)

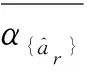
(19)

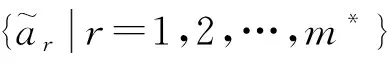
(20)

式中,d0和d1为拟合系数。需要注意,若同种规格的螺栓夹紧长度不同,则需要重新标定其最优尺度、权重系数及拟合系数。

2 试 验

2.1 试验系统

试验系统的组成如图4 所示。超声波脉冲信号源采用JSR Ultrasonic公司生产的PRC50脉冲发射板卡,超声波换能器采用日本奥林巴斯公司的接触式纵波窄带探头A112S-RM,中心频率为10 MHz。耦合剂采用与该探头匹配的B-2纵波耦合剂。数据采集应用了台湾ADLINK公司的AD-Link PCIE9852采集卡。将上述硬件与工控机集成后,使用LabVIEW完成数据采集系统的构建。CTM2200S拉伸试验装置可由工控机控制,该装置的配套压力传感器数据可由工控机读取。如图5 所示,选取两种不同长度的M8六角头螺栓试件作为试验对象,为了保证获得更加准确的超声波信号,将螺栓的两端做平整化铣削处理,并利用强力磁环与超声波换能器外环紧密贴合,保证试验过程中换能器与螺栓头部稳定耦合。试件的详细参数如表1所示。

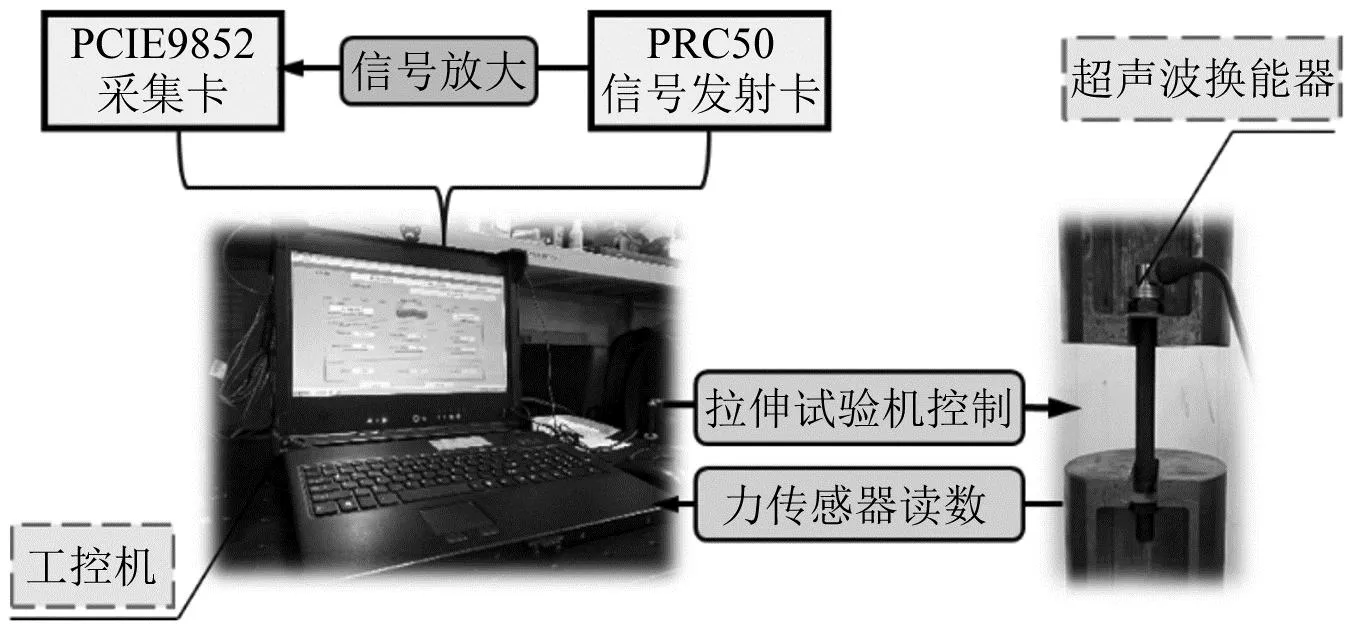
图4 试验系统的组成Fig.4 Composition of the test system

图5 螺栓试样Fig.5 Bolt specimens

表1 试件参数Tab.1 Parameters of test piece

2.2 信号处理

由于超声信号受应力影响产生的变化非常微小,而采集卡的最大采样频率为200 MHz,采样间隔内会损失部分信息。因此,采用希尔伯特变换获得超声回波的包络信号可以更加准确地提取信号峰值和渡越时间等信息。将采用希尔伯特变换[21]得到的超声回波信号的包络取模作为分析信号, 如图6所示。

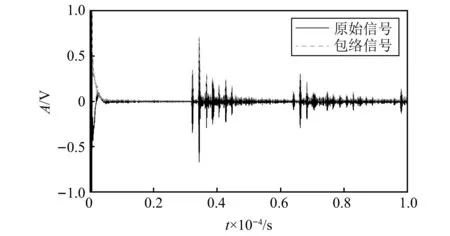
图6 希尔伯特变换获得回波包络信号示意图Fig.6 Schematic diagram of the Hilbert transform to obtain the echo envelope signal

2.3 螺栓参数标定试验

为了避免温度变化对材料衰减和声速的影响,整个试验装置位于实验室中,在参数标定试验期间以及下文的应力测量试验期间,通过中央空调保持环境温度恒定,将温度波动范围控制在1℃内。

由式(8)可知,在精确测量螺栓轴向应力之前,要对参数BL和CL进行标定。将激励电压设置为200 V,入射纵波的中心频率为10 MHz,使用拉伸试验机对两个螺栓试样进行加载,以10 MPa为步长,加载范围为0～200 MPa。

由于Daubechies小波族具有时频紧支撑、高正规性以及正交等特性,且对非平稳信号较敏感,因此Daubechies小波族更适用于超声波信号的处理。根据式(11)和式(12),采用DB小波分别对螺栓不同应力状态下的第一次底面回波f1(t)和第二次底面回波f2(t)进行小波变换,其分解层数为128,得到两次回波的系数矩阵F1(a,b)和F2(a,b)。然后根据式(13)计算两螺栓试样每组应力下每个尺度下的衰减系数。为了得到各个尺度下的衰减系数与螺栓承受轴向应力的关联度,采用灰色关联分析法,以应力序列X为系统行为特征序列,衰减系数序列(Y1,Y2,…,Y128)为相关因素序列,分辨率ξ为 0.5,根据式(15)和式(16),得到各个尺度的灰色关联度(γ1,γ2,…,γ128)。

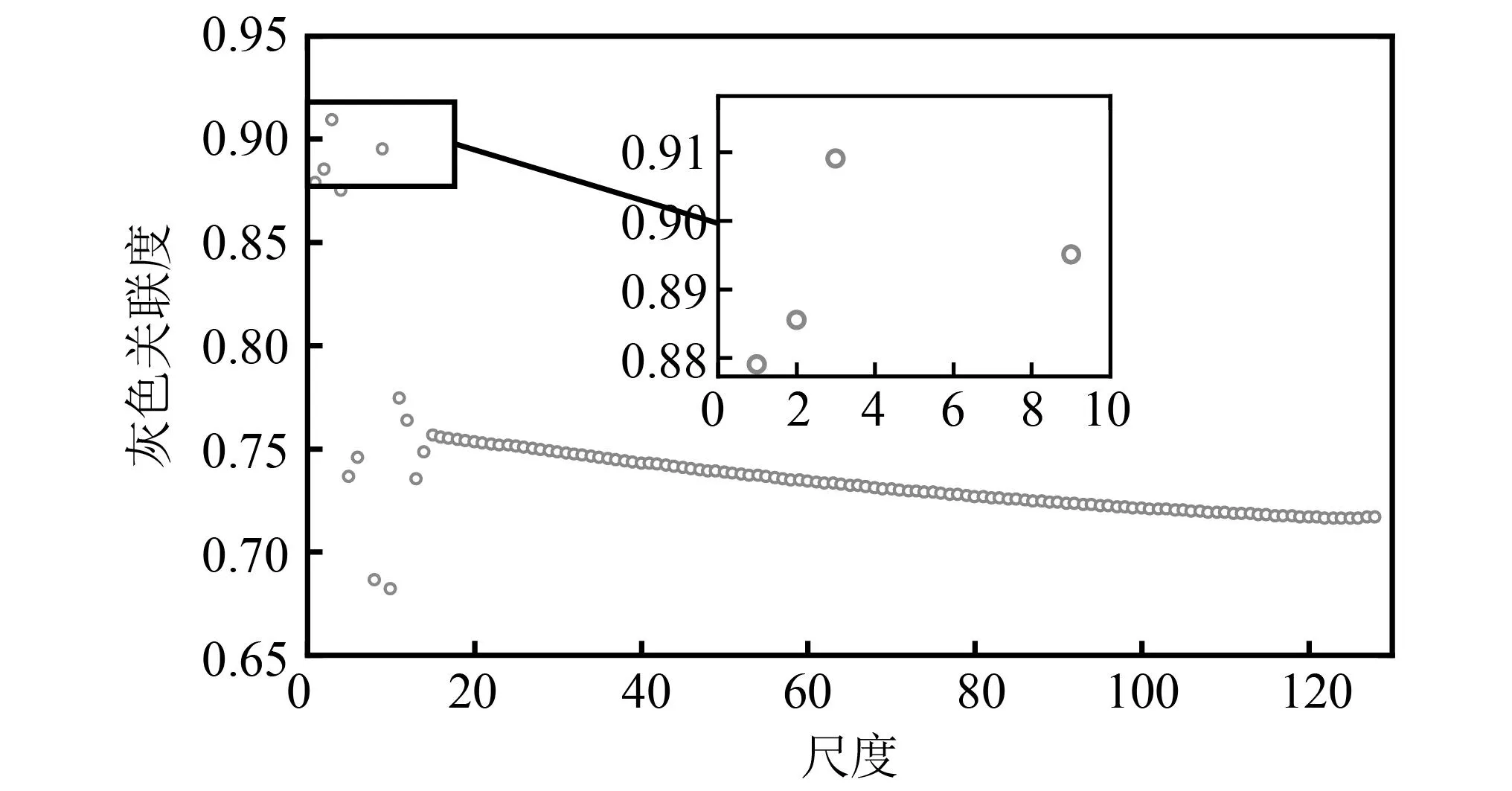
图7 尺度-灰色关联度Fig.7 Scale-Grey correlation

(21)

式中:Ωmax为初始惯性权重,取值Ωmax=0.9[23];Ωmin为至最大迭代次数时的惯性权重,取值Ωmin=0.4;T为最大迭代次数。根据文献[24],学习因子c1和c2均取1.494。

经过搜索后,归一化权重系数(w1,w2,w3,w9)分别为0,0.0002,0.8379,0.1619。代入式(14)得

(22)

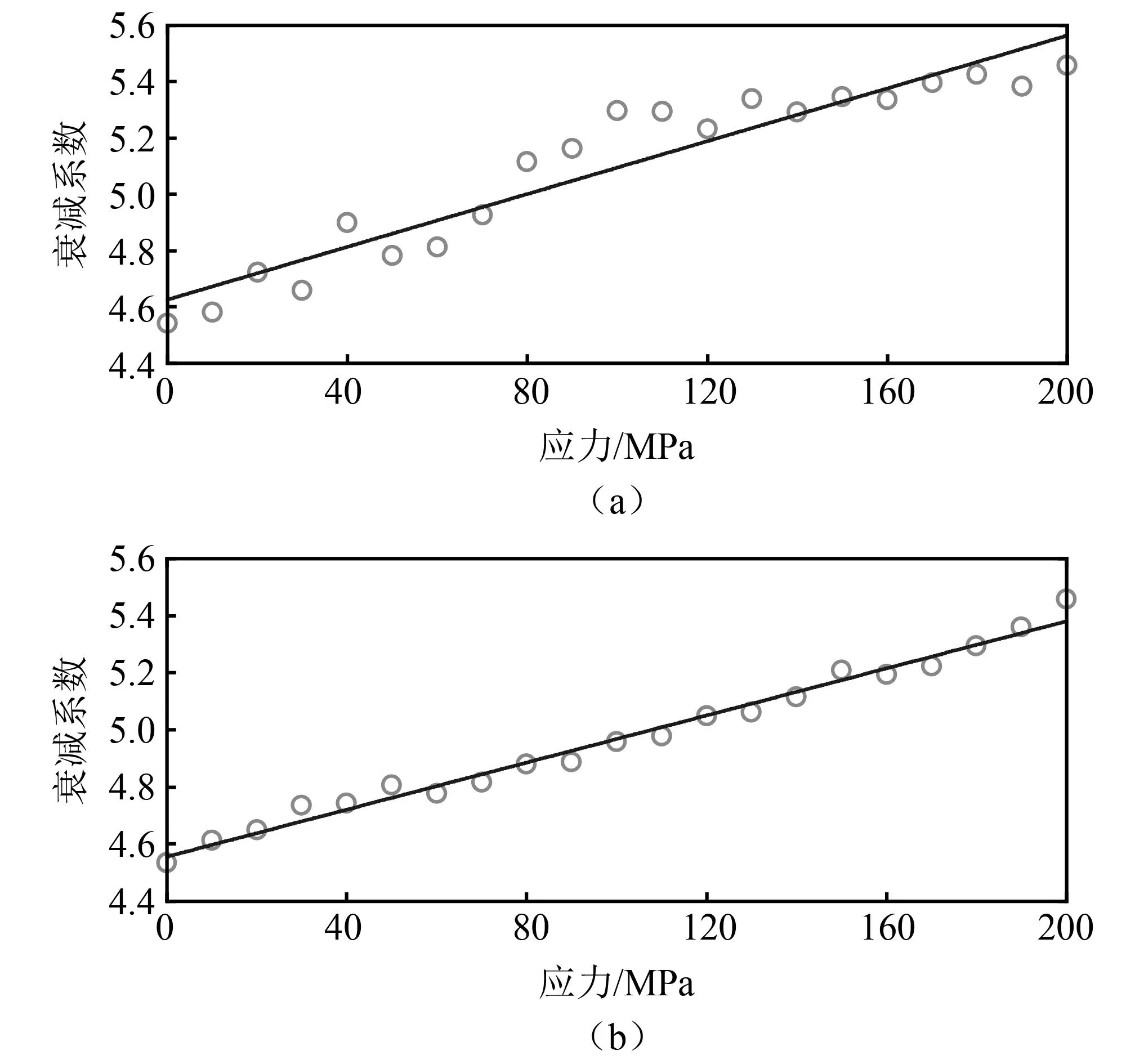
图8 应力-衰减系数拟合关系曲线Fig.8 Stress-attenuation coefficient fitting relationship curve

采用传统衰减法所得到直线模型的拟合优度R2≈0.900 7,而采用平均多尺度衰减法的直线模型得到了较大的改善,其拟合优度R2≈0.984 3。这说明采用平均多尺度衰减法对测量螺栓轴向应力的影响更具弹性。从而可以得到夹紧长度为 70.29 mm的试样 A轴向应力的平均多尺度衰减测量模型以及参数BL和CL的值。根据式(8)可知,BL和CL是影响测量结果的两个关键参数,必须准确标定其值。因此,测量了每个试样在3组不同夹紧长度下的BL和CL,并将其平均值和作为最终的参数校准值。

试件A和试件B在不同夹紧长度下轴向应力与平均多尺度衰减系数的关系,如图9所示。由图9可以看出,衰减系数随着轴向应力的增大而增大且具有较强的线性关系,且随着夹紧长度的增加,其拟合直线的斜率增大,与理论相一致。螺栓参数BL和CL的标定结果。观察表2中的数据可以看出,试件A的BL和CL与试件B相比略大,从而验证了式(6)和式(7)的正确性。因此,试件A和试件B校准模型分别为

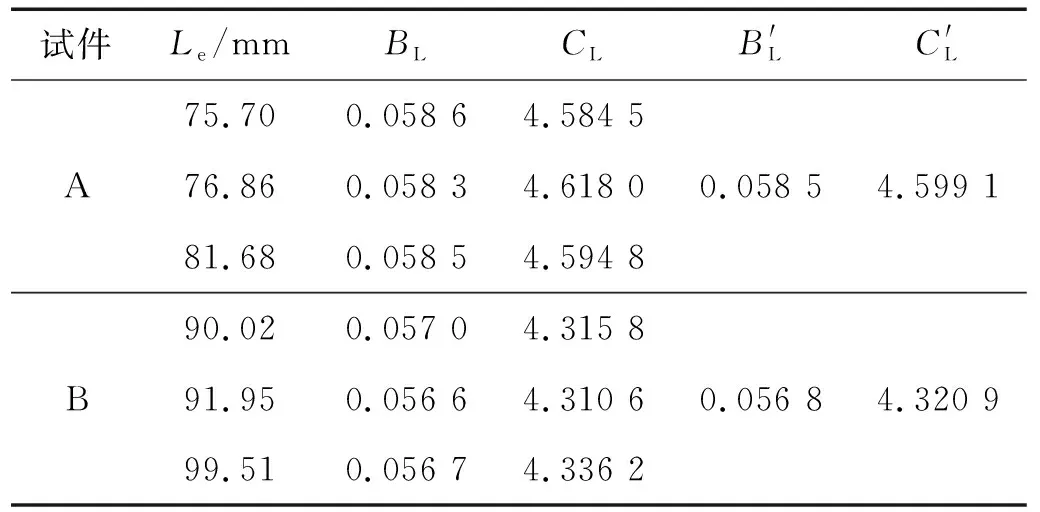
表2 螺栓参数标定结果Tab.2 Parameter calibration results of bolts

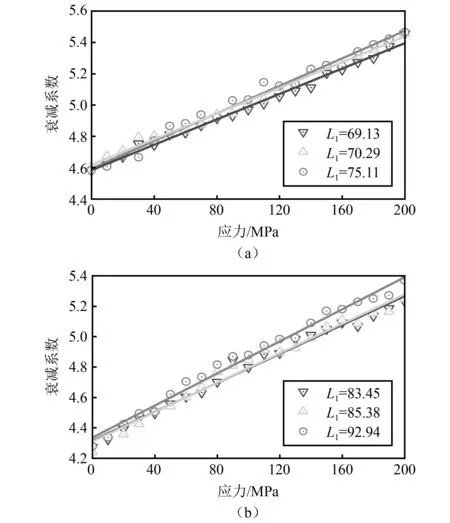
图9 试件A、试件B参数校正结果和拟合直线Fig.9 Specimen A and B parameter calibration results and fitted straight lines

(23)

(24)

2.4 螺栓轴向应力测量

重新选取一枚公称直径为8 mm,总长为94 mm的45号钢半螺纹六角头螺栓(螺栓)和一枚规格相同,总长为114.5 mm的螺栓(螺栓)作为测量对象。通过拉伸试验机给螺栓施加载荷,加载范围为0～200 MPa,跨度为20 MPa,并使用表2中的标定数据进行测量,其测量结果如表3所示。

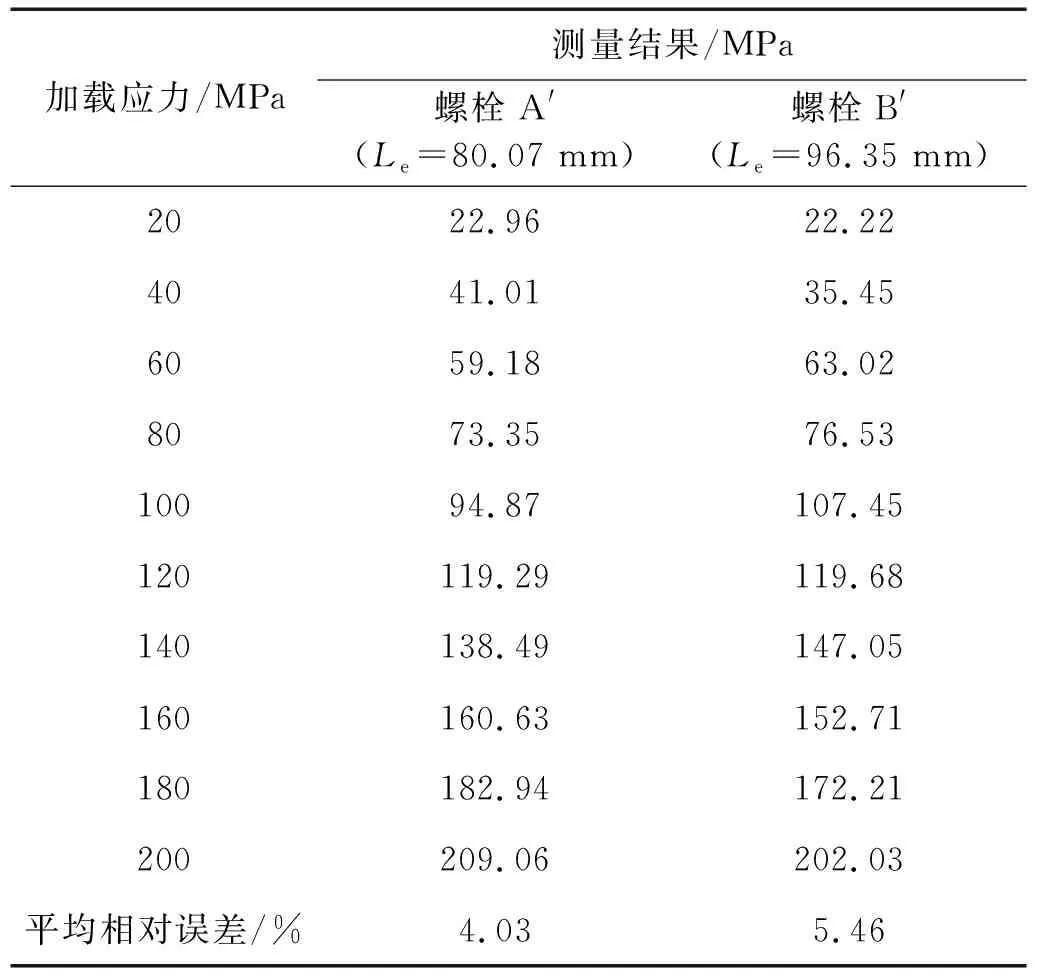
表3 螺栓轴向应力测量结果Tab.3 Bolt axial stress measurement results

表3展示了螺栓和螺栓轴向应力测量的结果。由表3可知,螺栓和螺栓的轴向应力测量平均相对误差分别为4.03%和5.46%,具有较高的测量精度。因此,通过平均多尺度衰减系数建立轴向应力的评估模型是可行的。

3 高强度短螺栓应力测量对比试验

为了说明此方法的优越性,对高强度短螺栓进行参数标定及应力测量,对比使用平均多尺度衰减算法前后以及单双波法的测量效果。通过拉伸试验机对高强度螺栓进行加载,其加载范围为0～200 MPa,步长为10 MPa,选取3组不同的夹紧长度,不同方法随应力的变化曲线如图10～13所示。由图10、图11可以看出螺栓轴向应力与声时差和声时比均存在线性关系,但曲线发生明显的阶梯状畸变。这是由于短螺栓刚度大,而且渡越时间的变化量小于采样周期,故无法得到其准确值。由图12、图13可以看出,多尺度衰减法的线性拟合优度明显高于传统衰减法。这是由于传统衰减法的回波信号中包含与轴向应力无关的信号成分,造成了一定程度的拟合误差。而多尺度衰减法有效滤除了上述无关信号成分,且对有效尺度组合进行归一化权重系数分配,有效地抑制了拟合误差。

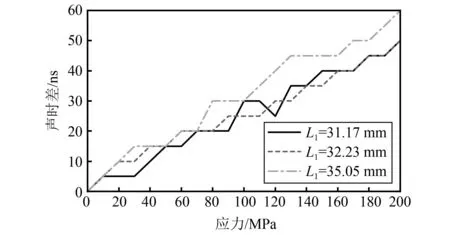
图10 高强度短螺栓声时差曲线Fig.10 Sound time difference curves for high-strength short bolts

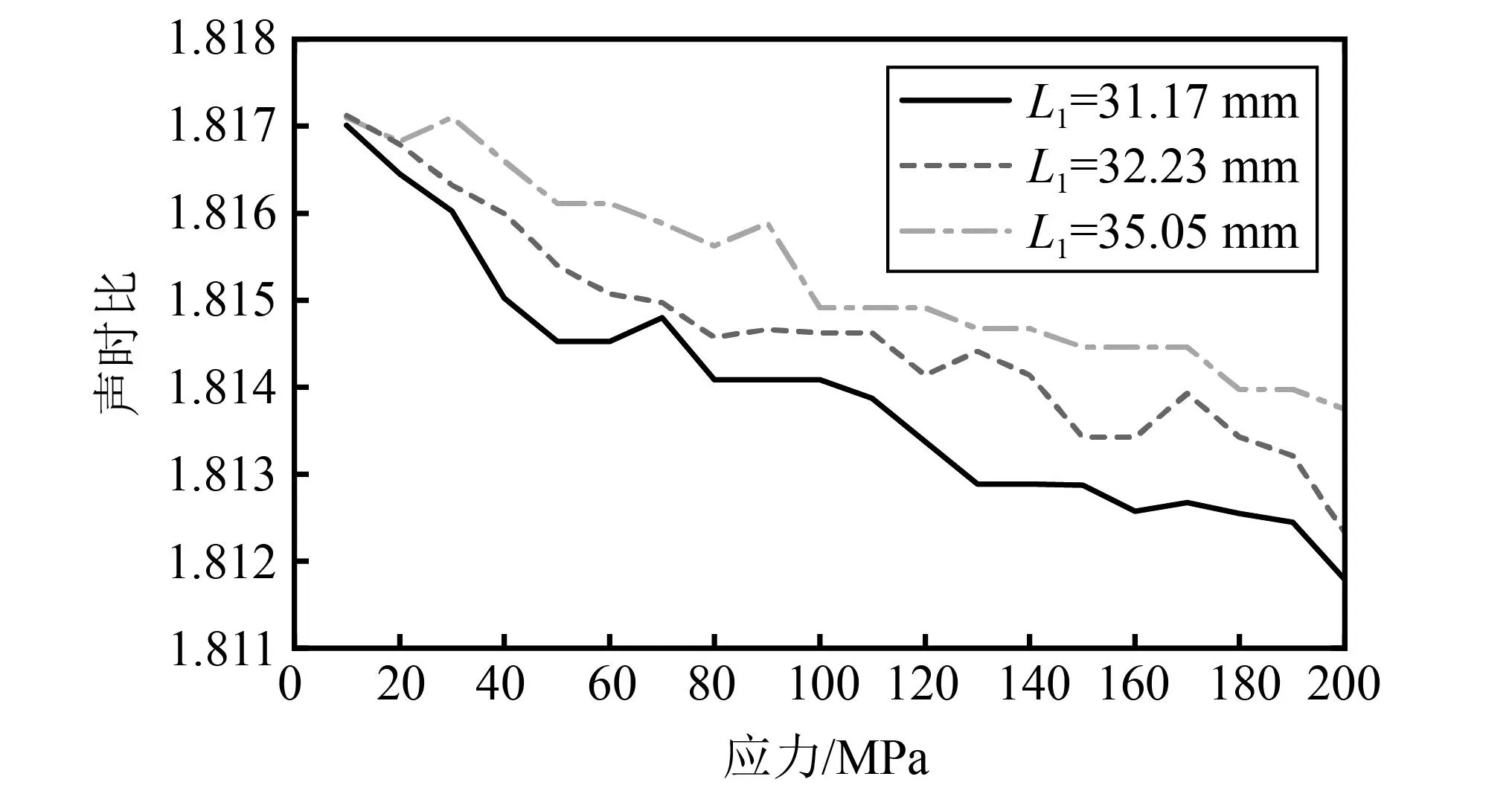
图11 高强度短螺栓声时比曲线Fig.11 Sound-time ratio curves for high-strength short bolts

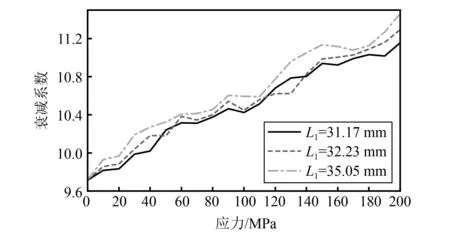
图12 高强度短螺栓传统衰减曲线Fig.12 Traditional decay curves for high-strength short bolts

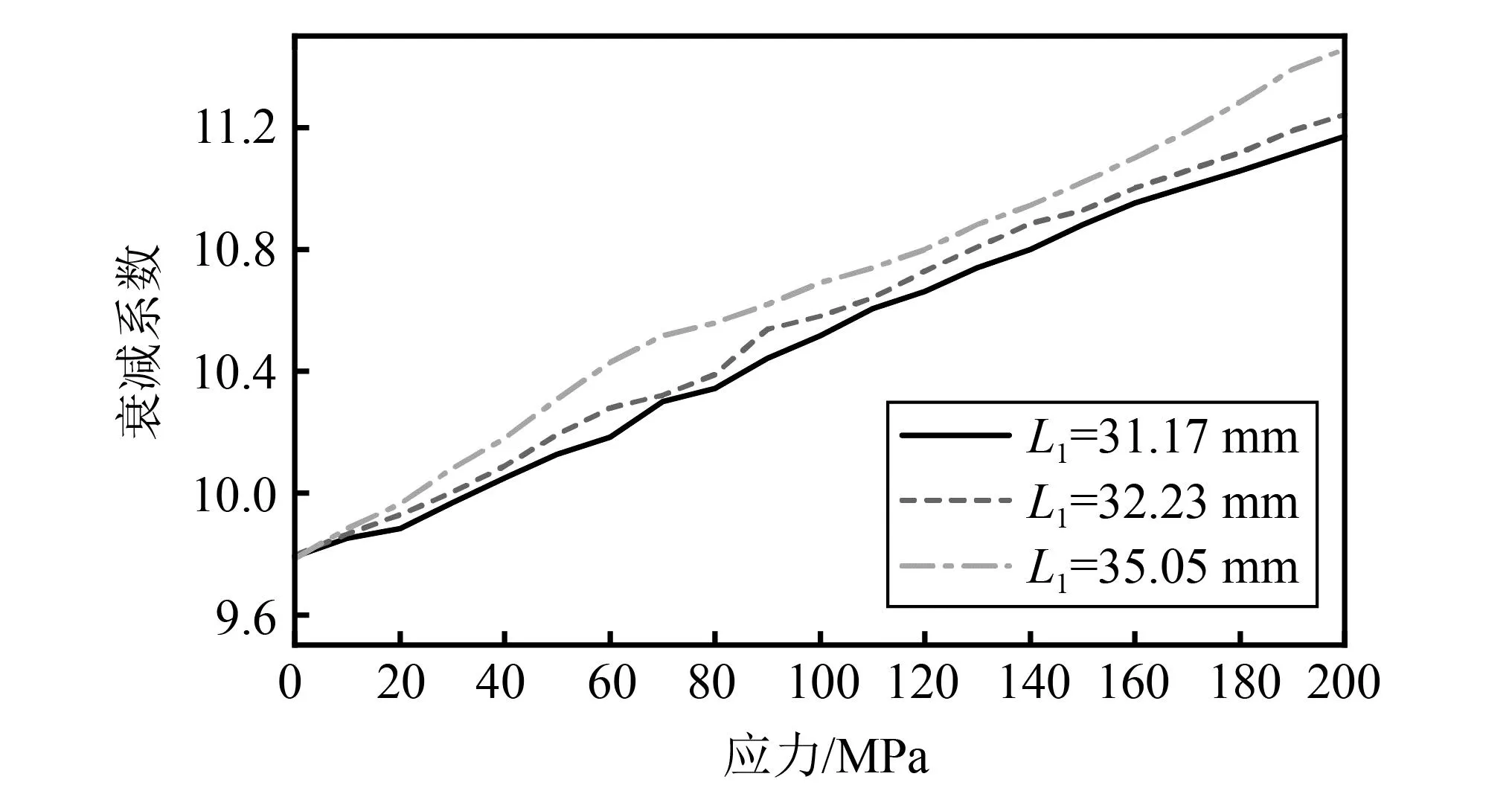
图13 高强度短螺栓多尺度衰减曲线Fig.13 Multi-scale decay curves for high-strength short bolts

根据2.3节参数标定的方法对高强度短螺栓进行参数标定,并由得到的校准模型进行应力测量。平均多尺度衰减法与单双波和传统衰减法的测量误差分析结果,如图14所示。由图14可以看出,当螺栓承受较高的载荷(大于60 MPa)时,多尺度衰减法轴向应力测量相对误差与其他方法相比明显减小,且测量精度较高。在实际工程应用中,高强度螺栓的承受载荷往往较高。因此,利用多尺度衰减法测量高强度短螺栓的轴向应力具有工程应用价值。

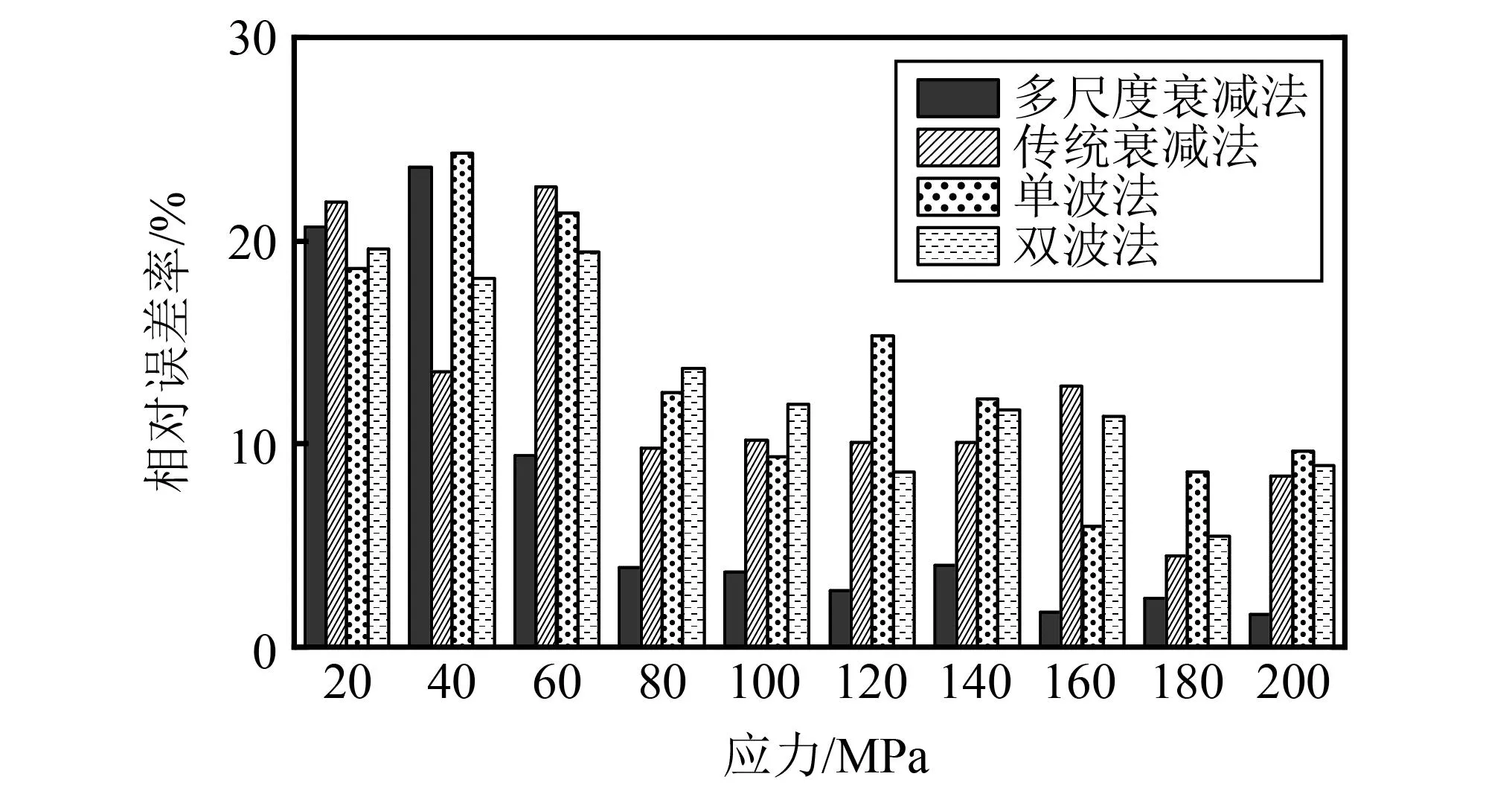
图14 测量误差分析直方图Fig.14 Measurement error analysis histogram

4 结 论

(1)分析超声波声时差法测量高强度短螺栓轴向应力的局限性,提出了平均多尺度衰减系数的新方法。综合利用与轴向应力相关度高的尺度下的超声波衰减特性对螺栓轴向应力无损测量,有效地排除了无关尺度的干扰,提高测量精度。

(2)结合灰色关联分析法以及粒子群优化算法,设计了基于最优尺度组合的归一化权重分配策略,并建立了轴向应力的超声多尺度衰减测量模型,有效抑制拟合误差对测量结果的影响。

(3)对普通的45钢螺栓试样以及高强度短螺栓进行参数标定和轴向应力测量试验,结果表明使用平均多尺度衰减算法后可以明显提高螺栓轴向应力的测量效果,具有适用范围广,误差更小的优势。本方法可应用于其他金属杆状轴向应力的测量。