基于Hessian局部线性嵌入和MLP-Mixer的液体火箭发动机涡轮泵轻量化故障诊断框架

窦 唯, 赵东方, 张宏利, 刘树林

(1.北京航天动力研究所,北京 100076; 2.上海大学 机电工程与自动化学院,上海 200044)

涡轮泵是液体火箭发动机的重要组件,是其推进剂输送系统的“心脏”[1]。随着航天技术的进步,涡轮泵的功率密度不断增加,加之恶劣的工作环境,导致其故障概率也随之增加[2]。因此,有必要探索先进有效的故障诊断技术以保障涡轮泵乃至整个运载系统正常运行[3]。

目前,在故障诊断领域,已有许多先进的分析手段被应用于各类机械设备中[4-6]。这些方法大多以振动信号为基础,大体上可分为基于信号处理的方法和数据驱动方法两大类。在信号处理方面,Hilbert-Huang变换[7]、小波分析[8]及卡尔曼滤波[9]等均被应用于涡轮泵故障诊断并取得了一定的成就。整体上,此类方法大多以特定的频率分量作为故障判据,因此对故障机理研究具有较强的依赖性。然而涡轮泵结构复杂,建模难度较高[10-13]。此外,涡轮泵机体振动信号强烈的噪声和非线性也使得以信号处理为基础的诊断技术更加难以应用。对于数据驱动类方法,早期一般依赖于SVM[14]及BP[15]等分类器,这些方法在一定程度上降低了对故障机理的依赖和信号非平稳特性的影响[16-17]。然而,上述分类器多为浅层架构,特征空间划分能力较弱,在一定程度上限制了诊断精度的提高[18-22]。

近些年,伴随着人工智能的浪潮,深度学习也被应用于机械故障诊断领域[23-26]。本质上,以深度学习为基础的诊断方法也属于数据驱动类方法,可依靠其强大的非线性映射构建能力自动建立故障数据与类别标签间的对应关系,从而获取优越的诊断性能[27-29]。然而,在应用于液体火箭发动机涡轮泵故障诊断的过程中,直接以原始时域信号作为深度学习模型的输入难以全面涵盖其在多个分析域的特性,后续信息挖掘难度较大。更重要的是,由于应用场景的特殊性,涡轮泵工作时间短且工况极端恶劣,故障演变迅速,只有快速判断装备运行状态才能够为主动控制等策略的实施创造可能。因此,相比于常规旋转机械,原始时域数据维数高且深度学习模型参数量大的问题在涡轮泵故障诊断中更加凸显,极易导致整个诊断框架难以收敛且计算量剧增,从而严重降低诊断效率。

针对上述问题,本文提出了基于Hessian局部线性嵌入(Hessian locally linear embedding, HLLE)和MLP-Mixer的液体火箭发动机涡轮泵轻量化故障诊断框架。在所提方法中,为更加全面地提取数据特征,分别计算了涡轮泵信号的时域参数、频域参数及时频域参数,并采用HLLE[30]算法进行降维,在保障信息全面性的前提下有效降低了特征维度。此外,在分类器选择方面,本文引入轻量化的MLP-Mixer[31]作为分类器。与其他深度学习模型相比,MLP-Mixer结构更加简洁,训练参数更少,且具有较为出色的分类性能。在试验部分,采用某型号真实涡轮泵的试车数据验证了所提方法的有效性。试验结果表明,与传统诊断方法相比,本文方法具有更高的精度优势,与其他深度学习类方法相比,所提方法能够在保障诊断精度的同时有效提高诊断效率。本文主要贡献如下:

(1)针对现有故障诊断方法特性参数选择片面及计算复杂度高等问题,提出了基于Hessian局部线性嵌入和MLP-Mixer的液体火箭发动机涡轮泵轻量化故障诊断框架。

(2)在所提方法中,综合考虑了液体火箭发动机涡轮泵时域、频域及时频域特征,并通过HLLE算法降低了特征矩阵维度,在保障信息全面性的前提下降低了数据冗余度。

(3)引入轻量化的深度学习模型MLP-Mixer作为整个诊断框架的分类器,在保留模型特征抽象能力的同时进一步降低了整个诊断流程的计算复杂度。

1 理论基础

1.1 Hessian局部线性嵌入

作为一种经典的数据降维算法,HLLE在ISOMAP的基础上对限制条件进行了一定程度的放宽,可得到局部距离相等的低维坐标。此外,该方法将局部的线性关系替换为局部的Hessian矩阵的二次型关系,成功解决了类似近邻数大于高维数据维度时导致权重系数不能保证满秩问题。图1给出了HLLE的示意图,其计算过程可概括为以下步骤:

图1 HLLE降维过程示意图Fig.1 Schematic diagram of the dimension reduction process of HLLE

步骤1确定邻域值

对每个样本数据xi,i=1,2,…,N确定其相应的邻域值k,并构造出样本数据集Xi=[xi1,xi2,…,xik]。

步骤2计算切空间坐标

步骤3计算Hessian矩阵

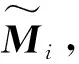
步骤4构造二次矩阵

利用步骤3计算出的xi所对应的Hessian矩阵Hi,i=1,2,…,n构造出其对称矩阵H。

(1)

步骤5计算矩阵H的零空间

对矩阵H进行特征值分解,并求出1～d+1个特征值及其相对应的特征向量u1,u2,…,ud+1,则U=[u1,u2,…,ud+1]为H的零空间。

步骤6计算对应的低维映射坐标

设矩阵Λ=(Λij)d×d,其元素为

(2)

式中,J为对应样本点的邻域集,且低维嵌入坐标可由式(3)给出

ψ=Λ-1/2UT

(3)

1.2 MLP-Mixer

MLP-Mixer是谷歌研究团队在2021年开发的一种纯MLP架构的神经网络,最初应用于CV领域的图像分类任务中。相较于当前主流的CNN架构中的卷积操作(Conv)和Transformer中的自注意力机制(Self-Attention),MLP-Mixer整体的结构更为简单。MLP-Mixer模型整体可划分为三部分,权值共享的全连接层、Mixer 层和分类模块。MLP-Mixer的框架如图2所示。

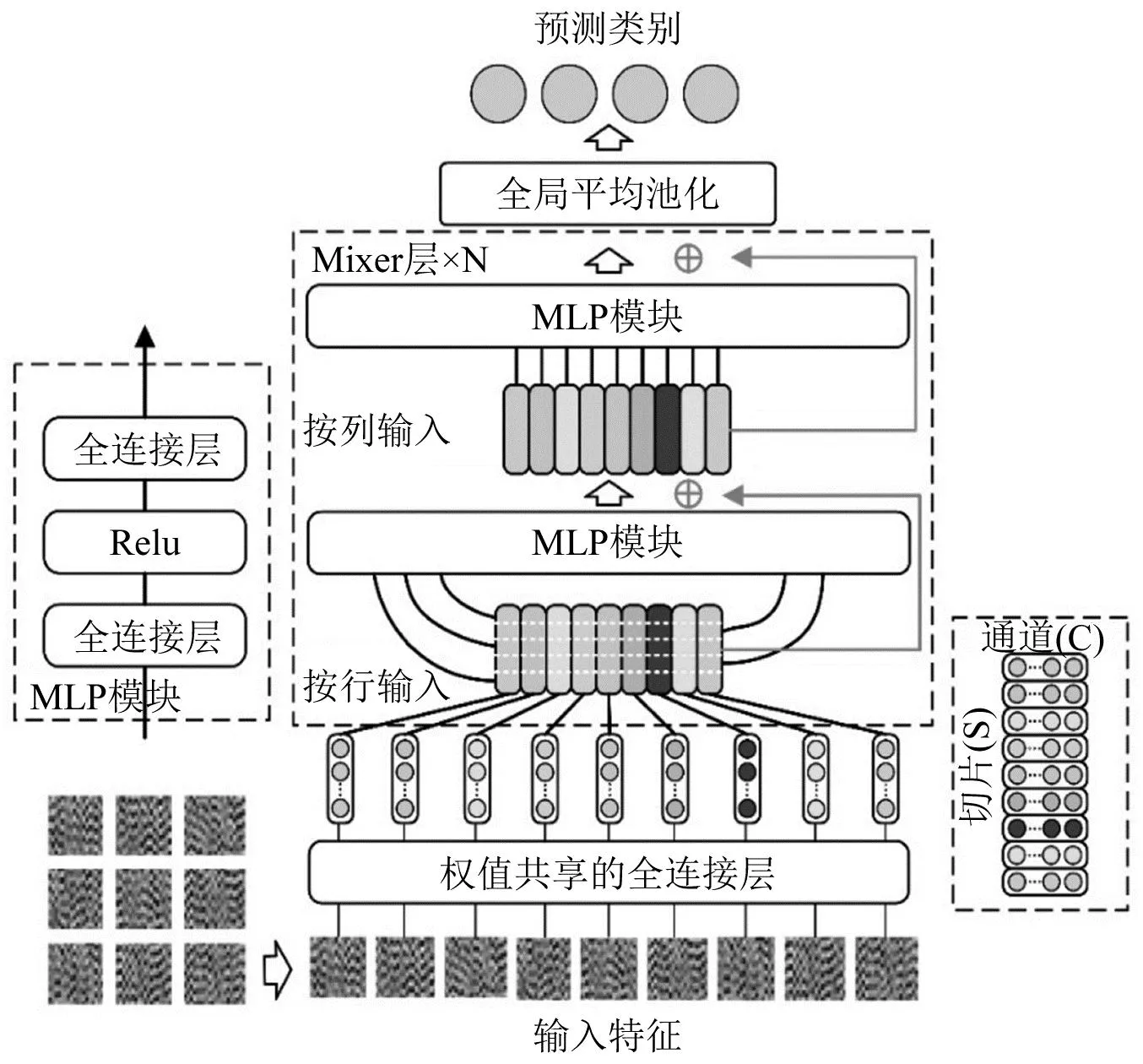
图2 MLP-Mixer模型架构示意图Fig.2 Schematic diagram of the MLP-Mixer model

权值共享的全连接层:全连接操作与卷积操作不同,只能获取对象的全局特征信息,并不能获取局部的特征信息。因此,当前的全连接层单独处理对象各区域的特征,然后在之后的处理过程中实现区域信息的融合。具体来说,如图2所示,原始的输入图片经过无重叠的分割后,将生成了S个子区域,每个子区域被称为一个patch。每个patch经全连接层(fully connected layers, FC)映射后得到一维的特征向量,向量长度为C。将每个patch 的输出结果组合后,我们得到一个S×C的矩阵。值得注意的是,处理每个patch的FC层是相同的,大大减少了模型训练的参数。权值共享的全连接层实现了输入特征从(H, W, C)到(S, C)的形状变换。

Mixer层:通过观察上一层的输出,可以发现矩阵(S, C)中的每一行表示输入对象在同一个空间位置不同通道上的信息,每一列代表不同空间位置在同一通道上的信息。因此,在(S, C)矩阵中,对每一行进行操作可以实现通道方向上的信息融合,对每一列进行操作可以实现空间方向上的信息融合。与传统卷积不同的是,Mixer Layer分开操作了空间域和通道域信息融合。首先,将(S, C)矩阵的每一列元素逐列输入到MLP1模块中,实现空间信息的混合。MLP模块由两个全连接层与一个激活函数组成。然后,将空间混合后的输出结果逐行输入到MLP2模块中,完成通道信息的混合。相较于步长为1的卷积核平移操作,Mixer层具有更高的特征提取效率。Mixer层的前向传播公过程可由式(4)及式(5)给出

U*,i=X*,i+W2×σ(W1×LN(X)*,i)

(4)

Yj,*=Uj,*+W4×σ(W3×LN(U)j,*)

(5)

式中:X为Mixer层的输入特征,形状为(S, C);LN( )为层归一化操作;σ为激活函数;W1、W2与W3、W4分别为MLP1与MLP2模块内两层全连接层的权重参数。

分类模块:MLP-Mixer模型的分类模块相对比较简单,主要采用传统的全局平均池化(global average pooling, GAP)、全连接层与Softmax激活函数组成。GAP的定义是在通道方向上,对每个通道内的所有特征值进行求和取平均,将平均值作为当前通道的输出特征值。分类模块的具体实现过程如图3所示。

图3 MLP-Mixer分类模块示意图Fig.3 Schematic diagram of the classification module

2 基于HLLE和MLP-Mixer的液体火箭发动机涡轮泵故障诊断流程

为提高涡轮泵故障诊断的精度并降低算法的时间复杂度,所提方法首先提取振动数据的时域、频域及时频域参数,并采用HLLE算法进行降维,在综合各项特征的同时控制诊断模型的输入维度。随后,降维处理后的特征被用于MLP-Mixer分类器的训练,相比于其他深度学习模型,MLP-Mixer结构更加简洁,有助于整个诊断框架的轻量化。图4给出了所提方法的整体流程,其详细步骤如下:

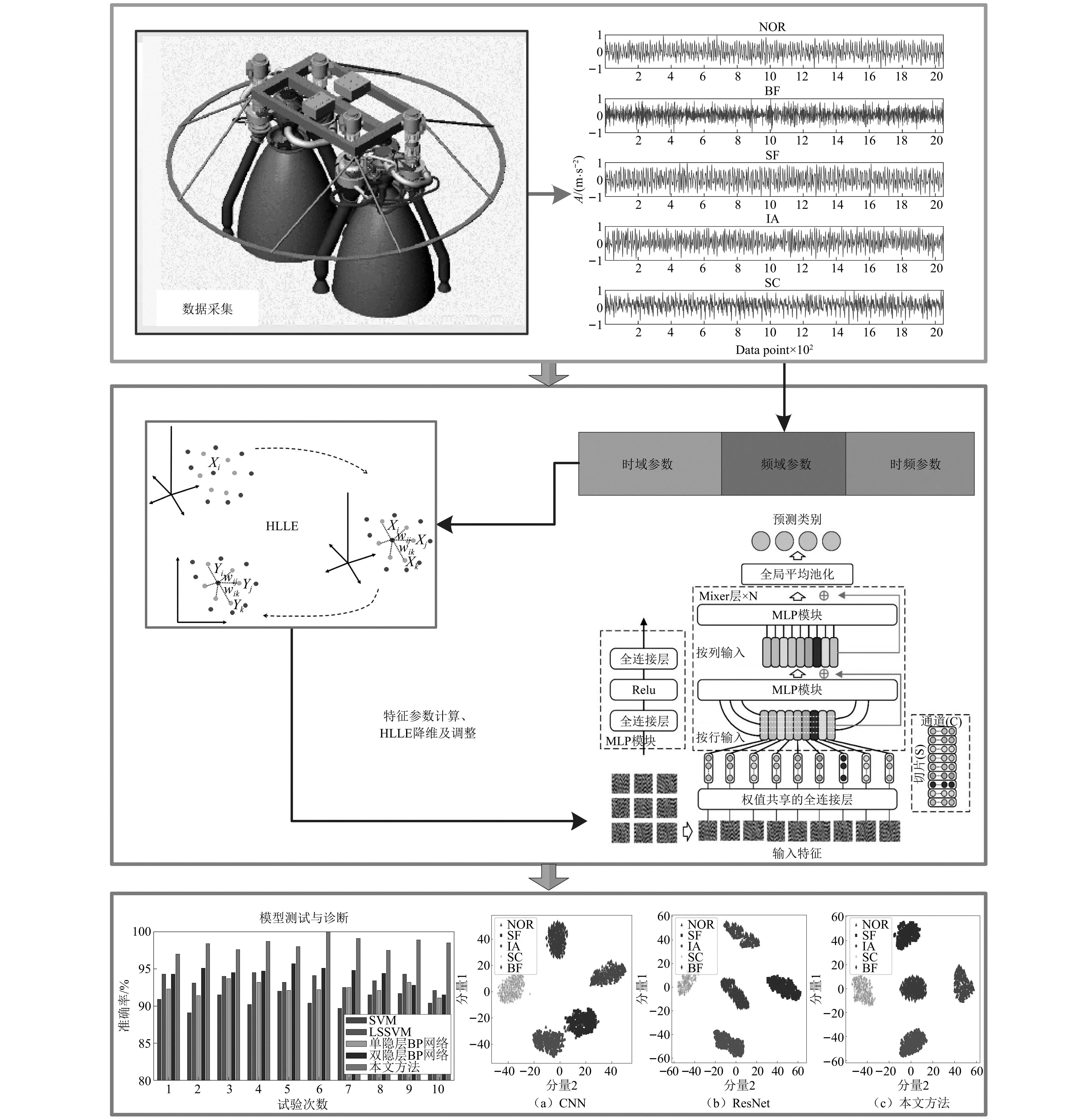
图4 所提轻量化故障诊断框架的整体流程Fig.4 Overall flow chart of the proposed lightweight fault diagnosis framework

步骤1利用加速度传感器采集涡轮泵振动数据,按照预设长度截取样本,并将其划分为训练集和测集。

步骤2分别计算训练集和测试集中样本的时域参数、频域参数及时频参数,利通过HLLE算法降维后利用训练集数据训练MLP-Mixer分类器直至收敛。

步骤3将测试集数据输入已保存的网络模型,对MLP-Mixer模型性能进行评估并输出最终诊断结果。

3 试验验证

3.1 试验设置

本节以某型号液体火箭发动机涡轮泵的试车数据为例验证了所提方法的有效性。试验过程中,振动加速度传感器安装在氧泵壳体外侧相对平坦的位置,信号采集系统的采样频率为50 kHz。试车过程中,共收集了5种状态下的涡轮泵振动信号,包括正常状态(normal,NOR)、轴承故障(bearing fault,BF)、轴断裂(shaft fracture,SF)、诱导烧蚀(inducer ablation,IA)和壳体裂纹(shell crack,SC)。在制作数据集的过程中,设置单个样本的长度为2 048且各个样本之间无交叠,每种状态下获得1 139个样本。表1和图5分别给出了试验发动机的设计参数和涡轮泵加速度测点位置。试验数据集的细节如表2所示,图6和图7分别给出了涡轮泵振动信号归一化后的时域波形和频谱。

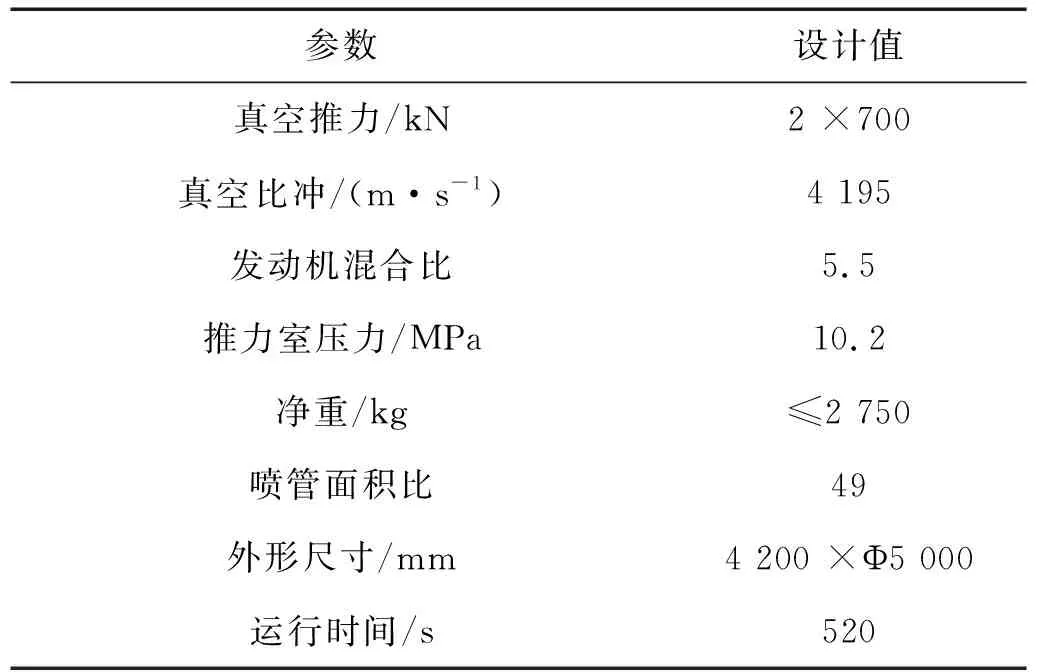
表1 试验发动机设计参数Tab.1 Design parameters of the test engine

表2 实验数据集Tab.2 Test data set

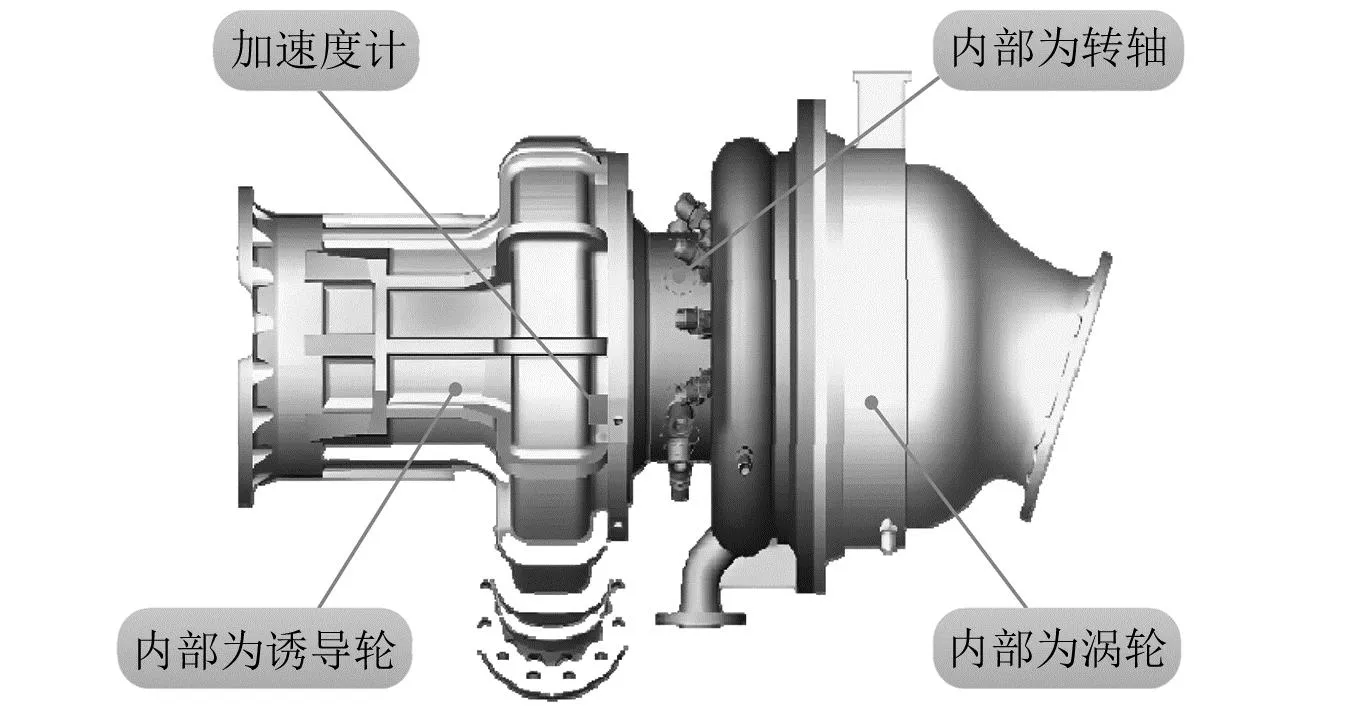
图5 加速度测点示意图Fig.5 Schematic diagram of the measuring points

图6 涡轮泵振动信号的时域波形Fig.6 Time domain waveform of turbopump vibration signal

图7 涡轮泵振动信号的频谱Fig.7 Frequency spectrum of turbopump vibration signal

3.2 特征参数选择及模型参数设置

液体火箭发动机涡轮泵结构复杂,运行工况极端恶劣,通过故障机理研究来确定有效的特征参数难度大,因此,为更加全面地考虑数据特性并保障算法稳定性,本研究中对原始信号的时域、频域及时频域参数进行提取,将提取的30个特征指标用来构建涡轮泵高维特征集,高维特征集构成如表3所示。其中,序号1～10为有量纲时域特征指标,序号11～16为无量纲时域特征指标,序号17～29为频域特征指标,序号30为时频域特征指标,且相关含义及说明可在文献 [32]中找到。

表3 特征集构成Tab.3 Composition of the feature set

在构建MLP-Mixer的过程中,本文主要采用MLP结构。此外,值得注意的是,在模型设计过程中,选用了卷积核尺寸、卷积步长与patch维度相等的卷积操作来实现权值共享的全连接层,以简化模型。MLP-Mixer模型架构的详细参数信息如表4所示。

表4 MLP-Mixer模型详细参数Tab.4 Detailed parameters of the MLP-Mixer model

在模型的训练过程中,学习率的取值十分重要,学习率设置不当,训练会出现过拟合、损失振荡剧烈等问题。然而,学习率的赋值与网络架构、数据集信息等都存在一定联系,关于学习率最优值的设定一直没有明确标准。为解决上述问题,本文设置了学习率减缓机制,实现学习率的平滑衰减。学习率减缓机制表现为:在训练初期,参数能快速定位到最优点附近。随着学习率不断衰减,参数逐渐逼近最优解。表5展示了学习率减缓机制的相关参数。

表5 学习率衰减机制相关参数Tab.5 Relevant parameters of learning rate attenuation mechanism

3.3 模型训练与性能分析

试验过程中,首先计算了不同状态信号的高维特征集,利用HLLE算法降至16维后将所得数据重新排列为4×4的格式用于MLP-Mixer模型的训练。训练过程中,随机选取数据集的70%作为训练集(训练集中的20%作为验证集),其余30%作为测试集,并采用10次试验的平均测试精度来评估算法性能。图8给出了某次训练中损失及识别精度的变化曲线。 如图8所示,在训练初期,损失下降及识别精度提高较为迅速,经过约15次迭代,基本达到较为理想的水平。在继续的迭代过程中,损失曲线及精度曲线的变化逐渐趋于平缓,在经过约30次迭代后,曲线只是在极小的范围内波动且趋势基本稳定,整个过程中验证准确率可基本稳定在100%。

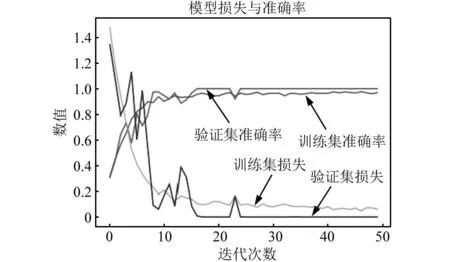
图8 训练过程中模型损失及精度变化Fig.8 Model loss and accuracy change during training

模型收敛后,将测试集数据输入模型以评估其性能。图9为该次测试的混淆矩阵,从图9中可以看出,对于5种不同的涡轮泵健康状态,绝大部分状态可以被准确识别,误诊样本仅出现在BF状态和IA状态之间,而其他状态之间没有出现误诊样本,本次测试精度为99.9%。

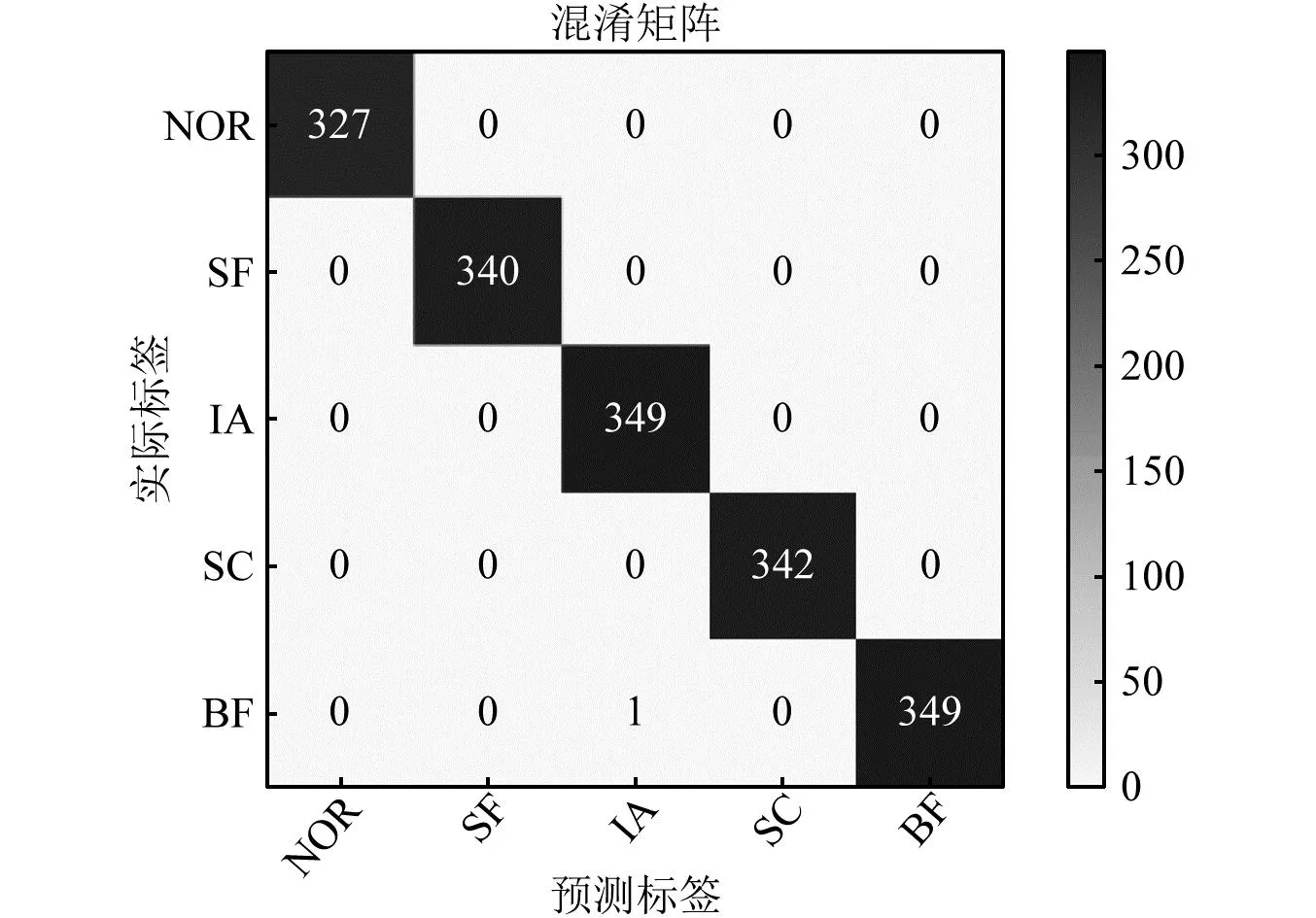
图9 测试集混淆矩阵Fig.9 Confusion matrix of test set

3.4 与经典方法的比较

为验证本文所提方法的优越性,本节将所提方法与故障诊断中较为常用的经典分类方法进行了比较。比较过程中,主要考虑了支持向量机(support vector machine,SVM) , 最小二乘支持向量机(least squares support vector machine,LSSVM)和反向传播(back propagation,BP)神经网络等方法。值得注意的是,所有方法均以未降维的高维特征集作为输入。此外,在使用BP神经网络的方法中,分别考虑了单隐层和双隐层两种结构,其中,单隐含层结构包含200个神经元,第二个隐含层包含100个神经元。值得注意的是,本文中SVM和LSSVM算法均采用了RBF核,并通过粒子群算法来确定最优的核参数及惩罚因子。对于SVM,核参数g1=4.37,惩罚因袭c1=12.72; 对于LSSVM, 核参数g2=3.44,惩罚因袭c2=15.08。对于BP算法,训练采用了传统的随机梯度下降算法,当验证集(训练集数据的10%)损失发生较为明显的上升趋势时判定模型泛化停止。试验过程中,为避免随机因素的影响,所有方法均进行10次试验,诊断结果如图10及表6所示。

表6 不同方法的平均识别精度Tab.6 Average accuracy of different methods

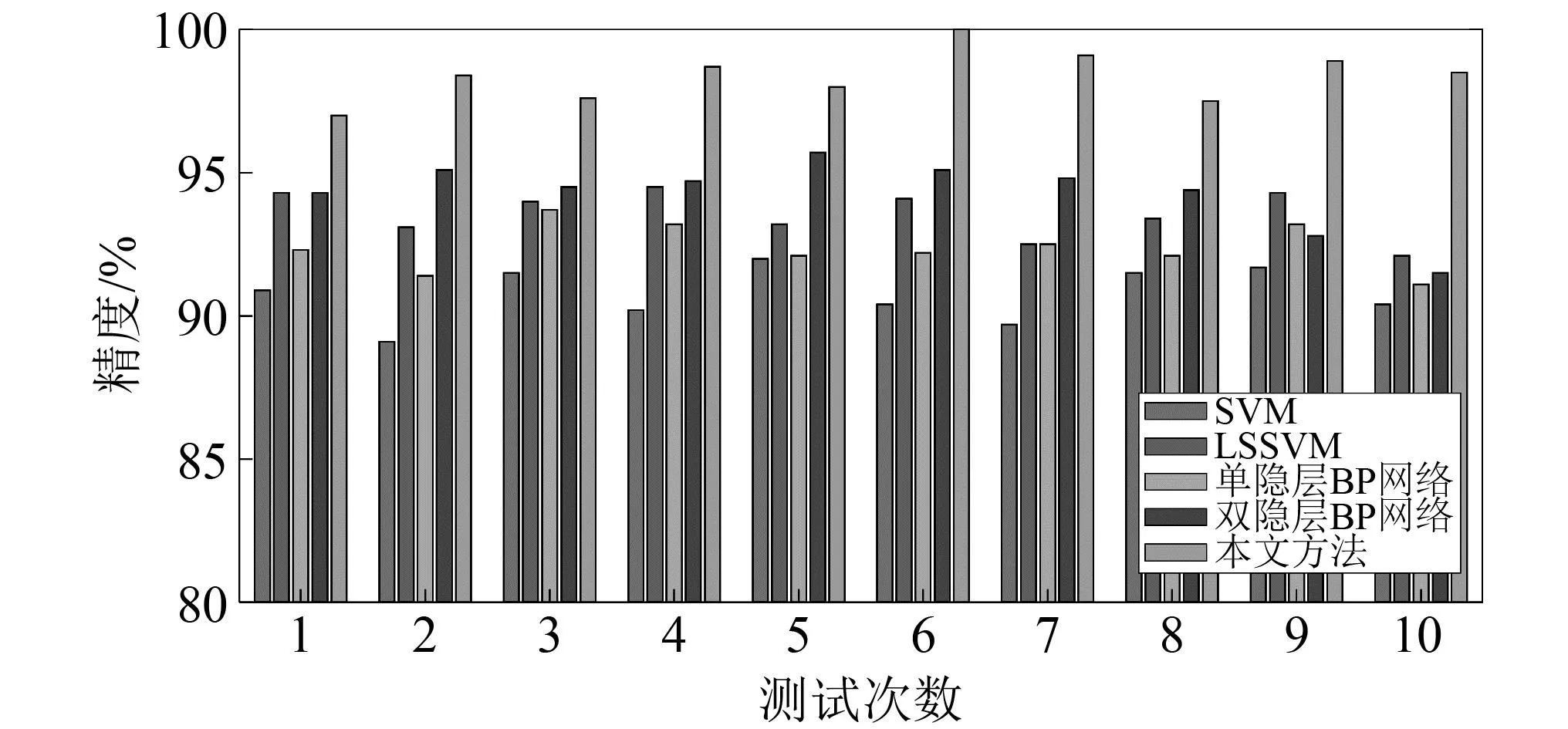
图10 不同方法的10次测试结果Fig.10 10 test results of different methods

由图10及表6可知,在10次试验中,本文方法均具有较为理想的识别正确率,且各次试验结果波动较小,平均识别准确率为98.4%。与本文方法相比,常规SVM方法的识别准确率有所下降,约为90%,而LSSVM的识别精度可达93.7%。在两种基于BP神经网络的诊断方法中,单隐含层BP网络的准确率为92.4%,这可能是浅层结构的局限所致。随着网络深度的增加,双隐含层BP网络的识别准确率有所提高,达到了94.3%,但与本文方法的98.4%依然存在较大差距。由上述分析可知,与常见的经典方法相比,本文方法具有较高的识别准确率和稳定性。

为进一步研究特征参数对算法性能的影响,不同特征参数下的诊断精度和时间,如表7所示。由表7可知,当仅使用时域或频域特征时,计算时间最短,但诊断精度也较低,仅为95%左右。当同时使用时域及频域特征时,诊断精度提升较为明显,为97.8%,而进一步加入时频域特征后,诊断精度仅有小幅提高,为98.4%,但整体性能更加稳定。由上述分析可知,特征参数的增加虽在一定程度上提高了计算复杂度,但有助于保障算法精度和稳定性。

表7 不同特征参数下的识别精度和时间Tab.7 Accuracy and time under different feature parameters

3.5 与深度学习类方法的比较

为进一步说明本文方法的优越性,将所提方法与DBN、CNN、LSTM-CNN、RseNet、ShuffleNet_V2及MobileNet_V2等深度学习方法进行了比较。对于所用DBN模型,主要由3个RBM组成,其中第一个RBM包含50个隐藏单元,而第二个及第三个RBM则包含100个隐藏单元。对于常规CNN,共包含3个Conv-ReLu-MaxPooling基本单元。其中,卷积层均含有32个卷积核,且卷积核的尺寸和步长均为4。在池化层中,池化区域的大小和步长均为2。对于ResNet, 则是在上述CNN基础上添加残差连接构成的。对于LSTM-CNN,则是在上述CNN最后一个池化层后添加了含有64个基本单元的LSTM层。对于ShuffleNet_V2,共包含3个基础模块,模块内部使用ReLU作为激活函数。对于MobileNet_V2,主要由3个瓶颈残差模块构成,且模块内部使用ReLU6作为激活函数。此外,在比较过程中,上述深度学习方法均以原始振动信号作为诊断模型的输入,且超参数设置与本文MLP-Mixer保持一致,10次试验结果如图11及表8所示。

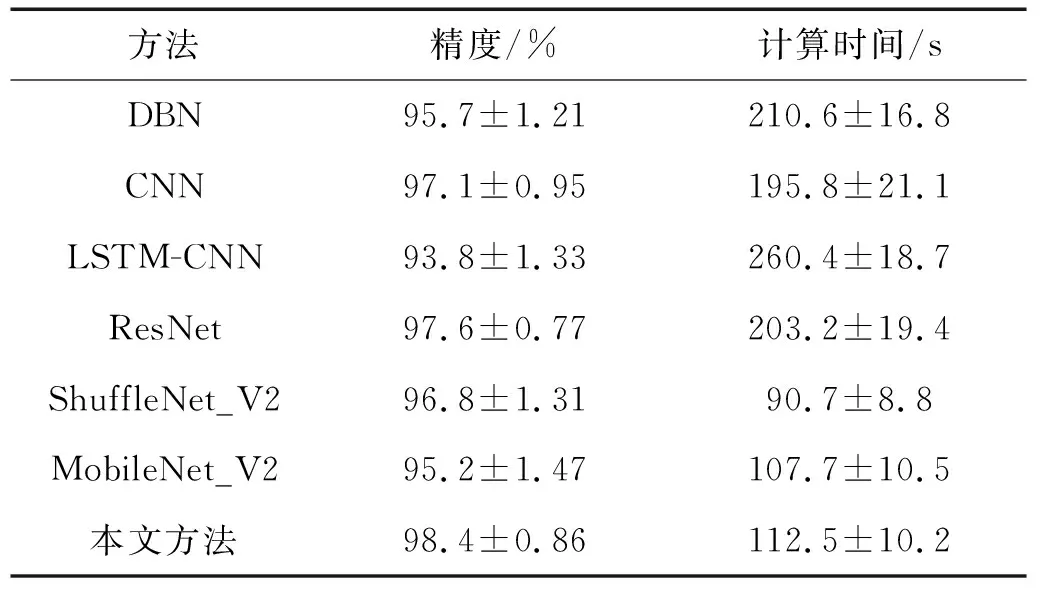
表8 不同方法的平均识别精度及计算时间Tab.8 Accuracy and time of different methods

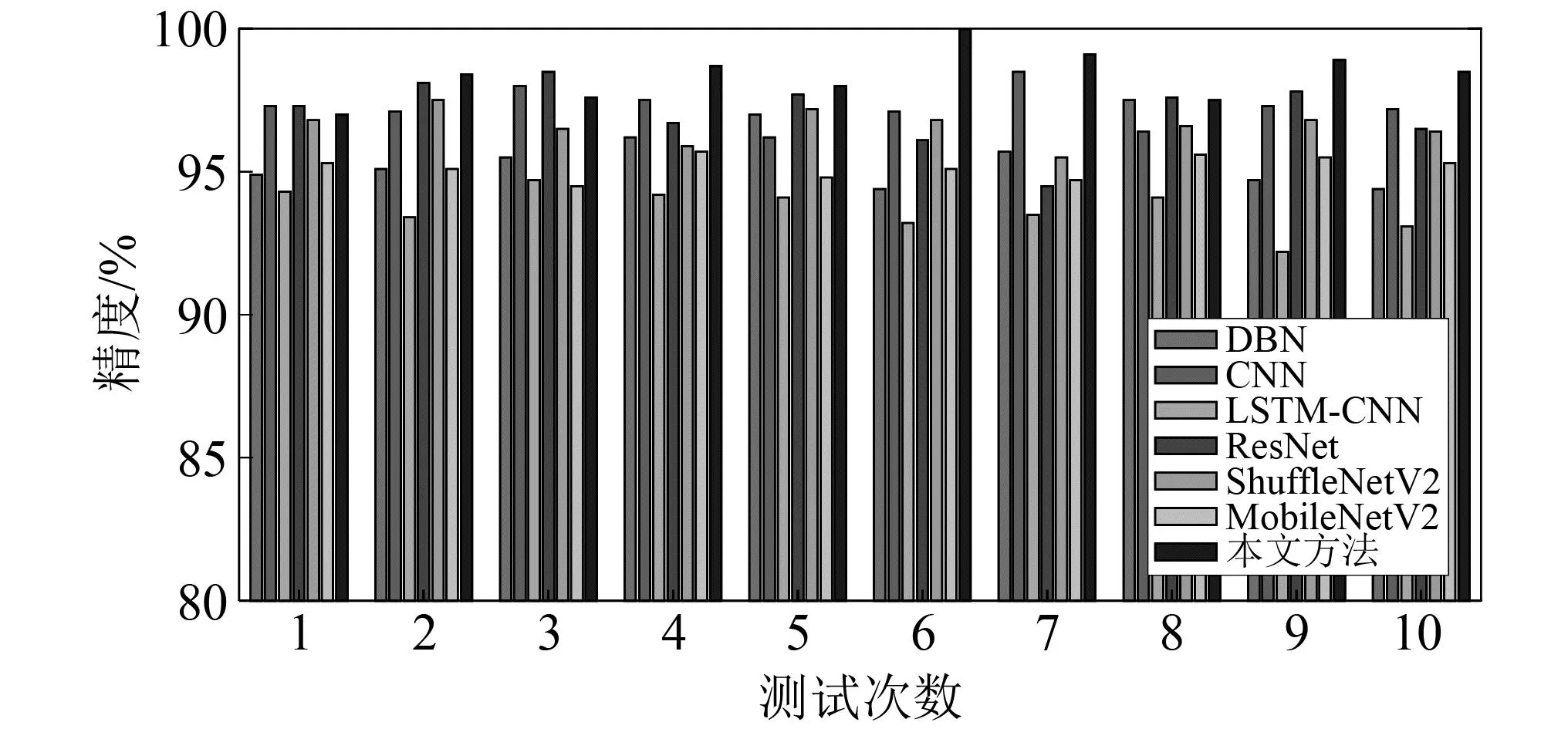
图11 不同方法的10次测试结果Fig.11 10 test results of different methods

由图11及表8可知,当输入为原始数据时,DBN和LSTM-CNN两种方法的识别精度均较低,仅为95.7%和93.8%,这与浅层分类器相比虽然具有一定的优势,但在深度学习类方法中却处于较低水平。与此同时,常规CNN和ResNet的识别精度分别为97.1%和97.6%,与本文方法的98.4%差距较小,均达到了较为令人满意的诊断效果。此外,在计算时间方面,LSTM-CNN耗时最长,约为260 s。值得注意的是,与轻量化模型ShuffleNet_V2及MobileNet_V2相比,本文所提诊断方法虽然在计算复杂度方面有所增加,但诊断精度优势较为明显。整体上,本文所提轻量化诊断框架的计算时间为112.5 s,能够在保障诊断精度的同时有效降低算法计算量,体现了本文方法的优越性。

不同模型特征图的t-SNE[33]可视化分析结果,如图12所示。由图12可知,CNN,ResNet和本文方法的可视化结果在形态上较为相似,5类涡轮泵数据在分类层之前的特征图经t-SNE处理后均表现出了较好的分离趋势,且不同类别数据间的分离边界均较为清晰,彼此之间差异不明显,这再次说明了本文方法在提高诊断效率的同时能够保障分类性能。

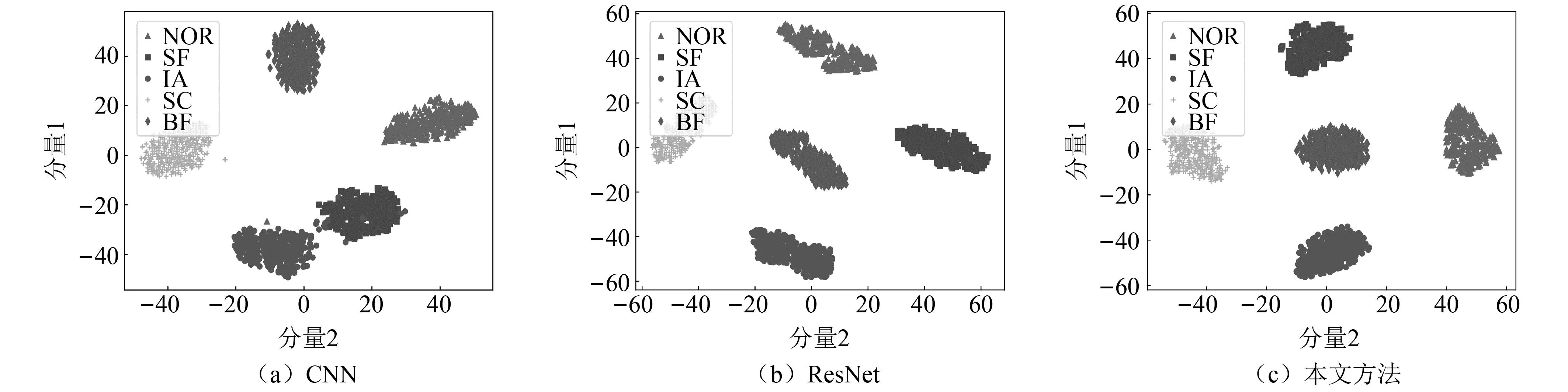
图12 不同方法的t-SNE可视化结果Fig.12 t-SNE visualization results of different methods

4 结 论

针对液体火箭发动机涡轮泵故障诊断中面临的特性参数选择片面及计算复杂度高等问题,本文提出了基于Hessian局部线性嵌入和MLP-Mixer的液体火箭发动机涡轮泵轻量化故障诊断框架。利用HLLE算法对信号的时域、频域及时频域特征进行降维,既全面考虑了信号特性又有效降低了数据冗余度。MLP-Mixer的引入,可以充分利用深度学习在特征抽象方面的优越性能,与此同时又降低了模型训练参数量,有助于整个故障诊断框架的进一步轻量化。通过某型号真实涡轮泵的试车数据验证了所提方法的有效性。试验结果表明,与传统方法相比,所提方法在识别精度方面具有显著优势,与其他深度学习类方法相比,本文方法能够在保障诊断精度的前提下降低计算复杂度,提高诊断效率。