多端柔直换流站高频谐振及传播机理分析与抑制

陈继开,孙崇博,李阳,张嘉扬

(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林省吉林市 132012)

0 引 言

随着“双碳”目标的提出,我国新能源发电技术突飞猛进,源-网-荷关键装备不断地“电力电子化”,电力系统正朝着“高比例可再生能源”和“高比例电力电子设备”的方向发展[1-2]。其中模块化多电平换流器(modular multilevel converter,MMC)凭借其模块化程度高、开关损耗低、扩展容量方便、可靠性高、输出谐波低等诸多优势[3-5],成为柔性直流输电(flexible high voltage direct current,HVDC)的关键装备,在高压远距离输电、新能源发电并网、偏远地区供电、城市电网互联等方面得到了应用[6-8]。然而由于MMC桥臂级联子模块数量众多,且内部特性复杂,由此带来的系统稳定性问题也不容小觑。例如,欧洲INELFE工程出现的1.7 kHz[9]高频振荡,我国鲁西背靠背柔直工程出现的1 271 Hz[10]、渝鄂工程中的1 810 Hz[11]、张北工程中的3 550 Hz[12]、如东工程中的2 000 Hz高频振荡等[13]。上述高频振荡问题不但导致换流站闭锁或保护误动作,严重时甚至可能威胁柔直系统运行安全[14]。

由于阻抗分析法物理意义清晰,能够解释电力系统振荡机理,因此被广泛采用以分析MMC系统的稳定性问题[7,15]。建立恰当的系统阻抗模型是阻抗分析法的重要一环,文献[16-17]基于谐波状态空间理论构建了考虑交流网络、系统链路延时、控制器参数的MMC谐波状态空间模型;文献[18-19]采用谐波线性化法,考虑锁相环、功率外环、电流内环等环节对MMC进行了阻抗建模;文献[20]考虑上述环节的同时,又计及MMC内部动态特性应用谐波线性化法给出了MMC交流侧阻抗解析模型。上述阻抗建模方法考虑影响因素多、建模比较精确,但是建模过程过于复杂。因此在系统高频谐振研究中,应采用考虑系统链路延时、电流内环、电压前馈等环节的MMC简化阻抗模型,在保留系统高频阻抗特性的前提下,降低模型的复杂度[7,9]。

对于MMC-MTDC系统,当MMC交流侧出现谐振时,考虑到交/直流侧系统间谐波存在相互作用[21-22],文献[23]基于平均值模型和调制原理,分析了300 Hz左右的交直流侧谐波传递特性,并对交直流侧新产生的各次谐波的幅值和相位进行了计算;文献[24-25]通过应用动态相量对MMC的序分量进行建模,并分析了三相不平衡时MMC的5次正负序的谐波传递特性;文献[26-27]通过MMC内部桥臂电压和谐波环流主要分析了6k±1次谐波的传递叠加特性。但上述文献多聚焦于MMC交直流侧谐波传递的研究,且多集中于中频段,而对于MMC-MTDC站间的高频谐振扰动能量传播问题鲜有涉及。

本文就空载线路投入条件下的多端柔性直流(modular multilevel converter multi-terminal direct current,MMC-MTDC)输电系统的高频谐振及其扰动能量传播问题开展研究。通过建立包含链路延时等环节的MMC阻抗模型,运用阻抗分析法阐释MMC高频谐振产生的机理。基于受端MMC的联合建模,通过探索高频扰动在各MMC控制器间的传播路径,分析高频谐振对不同控制类型MMC的影响机理。通过采取电压前馈串带阻滤波器的策略达到对高频谐振抑制的目的。最后借助仿真平台验证谐振分析理论及所提抑制策略的正确性与有效性。

1 多端柔直系统高频谐振问题

1.1 典型MMC-MTDC结构

MMC-MTDC是由3个及以上的MMC通过线路连接组成的高压输电系统,其显著优势在于,可以进行多电源供电和多落点受电。根据拓扑结构的差异性,将MMC-MTDC主要分为串联型及并联型,其中并联型结构又可细分为辐射型及环网型2种[28]。并联型系统要求各MMC直流侧电压相同,因此需其中一个MMC承担对系统电压支撑的任务。相较于串联型,并联型具有有功损耗小、调节范围大、故障恢复能力快、与系统绝缘容易配合、易于扩建、经济性好等诸多优点,其在工程中已得到广泛应用[29]。

1.2 MMC-MTDC高频谐振问题

目前柔直系统运行中曾多次发现高频谐振现象,频率范围从350 Hz到4 000 Hz不等,不但频率跨度宽、影响范围广、而且对应的抑制策略研究难度较大。其中渝鄂柔直和张北柔直出现的高频谐振现象较为典型。2018年,渝鄂柔直电网工程在分别对渝、鄂两侧进行空载加压试验时,两侧出现了700 Hz和1 800 Hz频率附近的高频谐振[11]。其现场波形如图1(a)所示。

图1 MMC典型高频谐振现象Fig.1 Typical high-frequency resonance phenomenon of MMC

2020年张北柔直系统中诺英线投入,康保站出现了1 500 Hz频率附近的高频谐振[30],现场录波如图1(b)所示。在后续对康保站的现场试验中,直流系统带空母线工况下又出现了3 200 Hz的高频谐振。

本文以多端柔直电网为工程背景,探究当采用下垂控制的MMC3发生高频谐振时,对其他受端MMC的影响。为便于后文仿真研究,基于RT-LAB5600实时在线仿真平台,搭建了四端并联型MMC-MTDC系统,如图2所示。

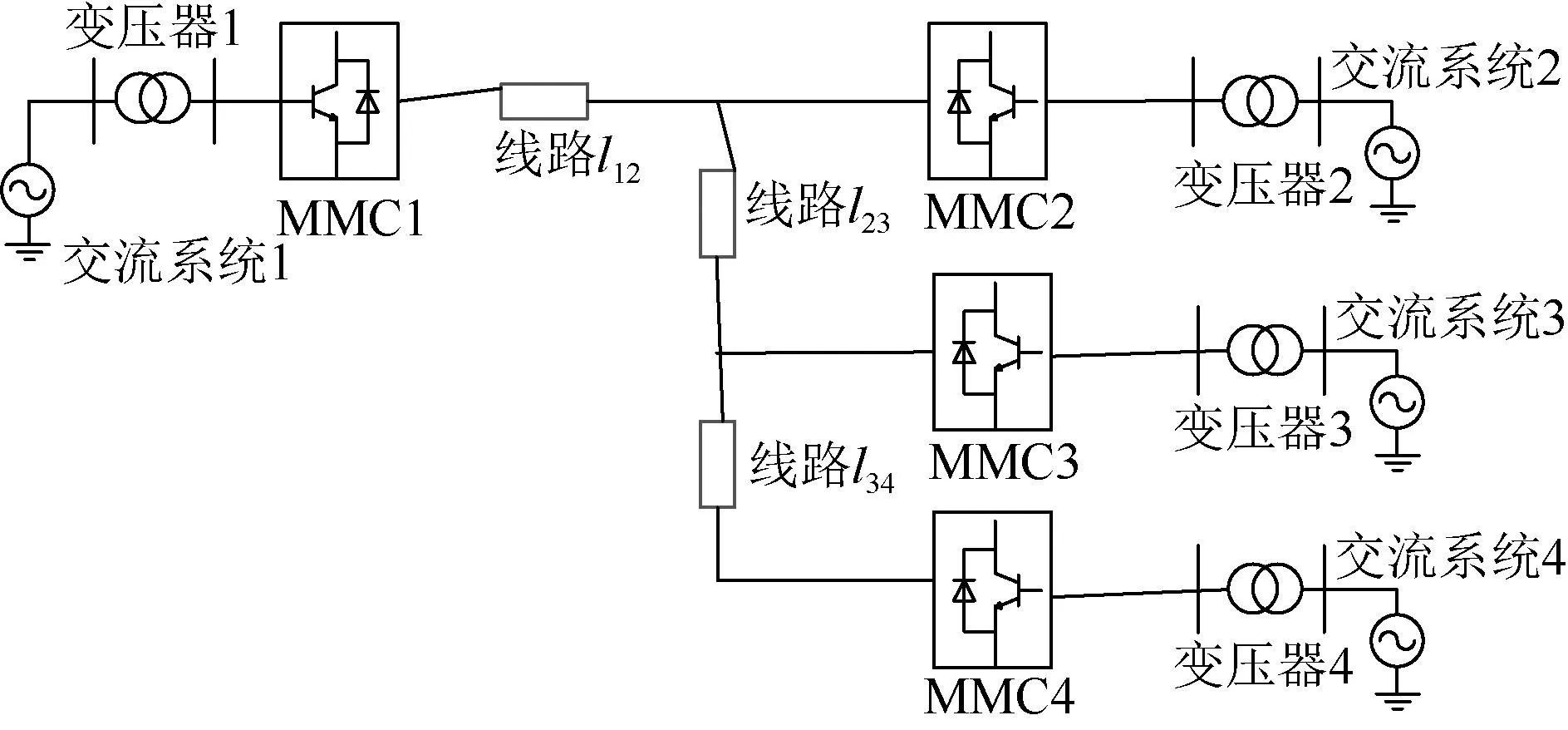
图2 四端MMC-MTDC系统仿真模型Fig.2 Four terminal MMC-MTDC system simulation model

2 柔直系统MMC高频阻抗建模

2.1 MMC典型控制系统结构

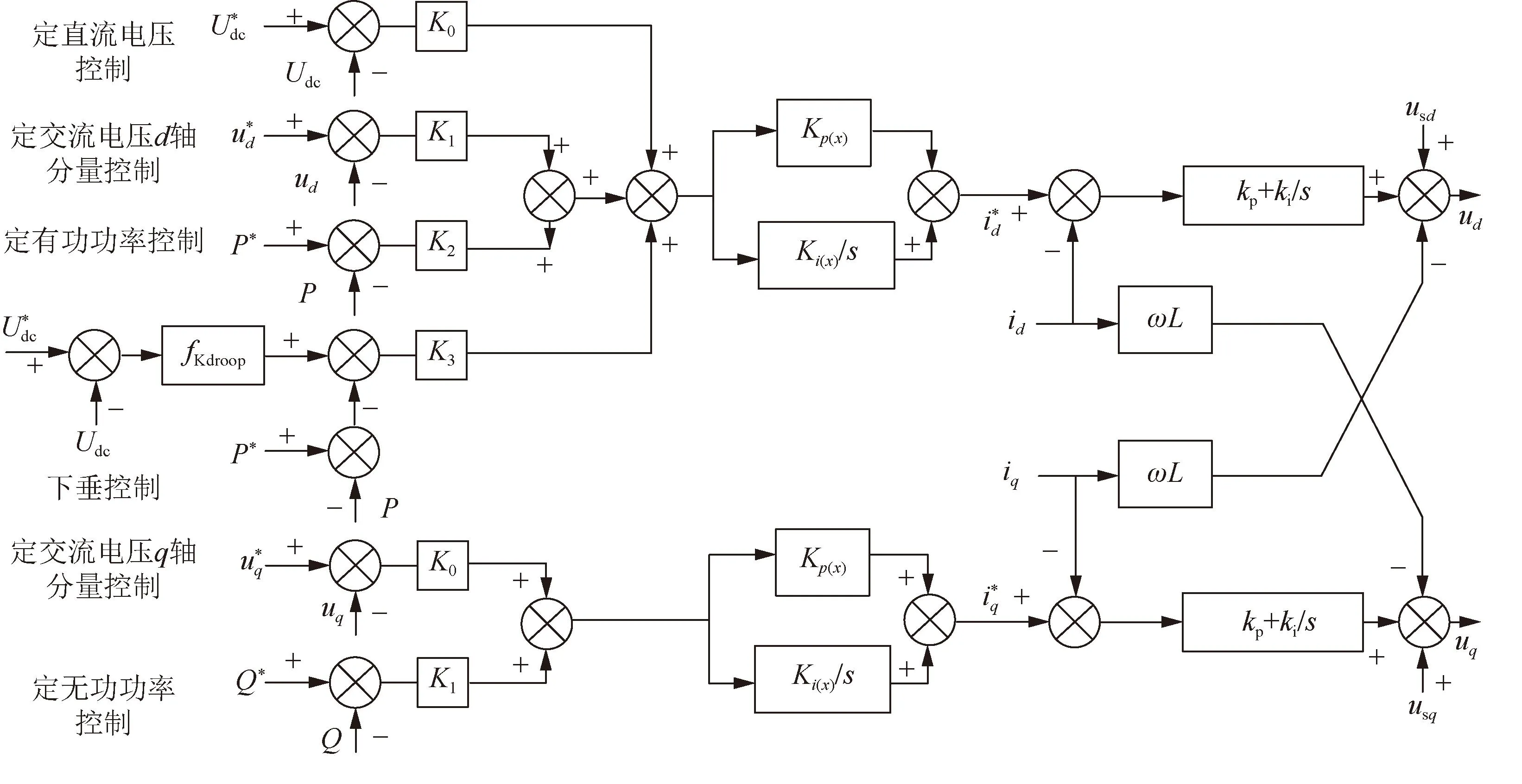
图3 MMC控制器结构框图Fig.3 Structure block diagram of MMC station controller

2.2 MMC高频简化数学模型

针对出现在100～3 000 Hz范围内的柔直系统谐振问题,考虑了电流内环、电压前馈、控制延时、控制通道滤波的MMC高频阻抗简化模型与详细电磁暂态模型的阻抗频率响应基本一致[9,31]。因此在对MMC交流侧阻抗进行建模时,可忽略功率外环、环流抑制和锁相环等环节对MMC阻抗的影响,得到考虑桥臂阻抗、电流内环、电压前馈、控制延时的MMC高频简化模型[7],如图4所示。

图4 MMC高频简化模型Fig.4 MMC high-frequency simplified model

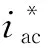
(1)

可得MMC高频简化阻抗模型:

(2)

式中:Leq=Larm/2;Req=Rarm/2;Larm、Rarm分别为桥臂电感、电阻。

3 柔直换流站高频谐振机理与站间传播影响分析

3.1 MMC高频谐振机理分析

由戴维南定理或诺顿定理可知,在投入空载线路前,交流系统及MMC可作等效电路,如图5(a)所示。MMC进行诺顿等效,io(s)、ZMMC(s)分别为等效后的理想电流源及MMC阻抗;交流系统进行戴维南等效,vg(s)、Zg(s)分别为等效后的理想电压源及交流系统阻抗。投入空载线路后,交流系统及MMC等效电路如图5(b)所示。

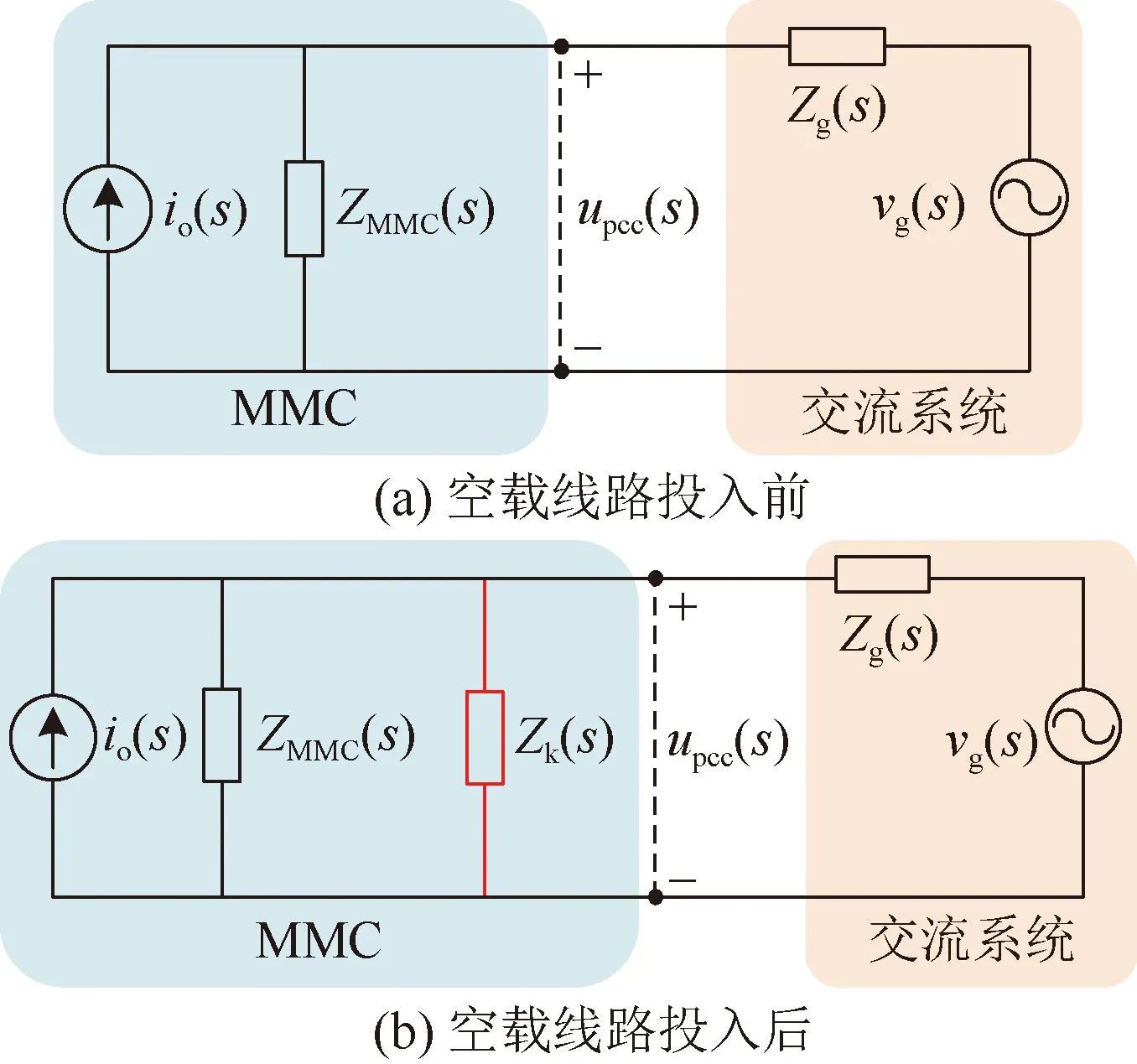
图5 空载线路投入点等值电路Fig.5 Equivalent circuit point of unloaded line input

交流线路通常采用串联n个π型等值电路来进行简化等效,通常取n=20模拟交流线路的特性[30],Zk(s)为投入的空载线路的等效阻抗。投入空载线路后,MMC交流侧等效阻抗为:

Zo(s)=ZMMC(s)//Zk(s)

(3)

根据阻抗分析法[32],若Zo(s)和Zg(s)的幅值存在交点,并且在幅值交点的频率交接处若满足两者相位差大于180°,则系统在频率交接处发生相应频率的谐振;反之,若不满足上述任一条件,则系统稳定。

根据下文表1提供的系统参数,由式(3)可得投入空载线路后的MMC交流侧等效阻抗Bode图,如图6所示。

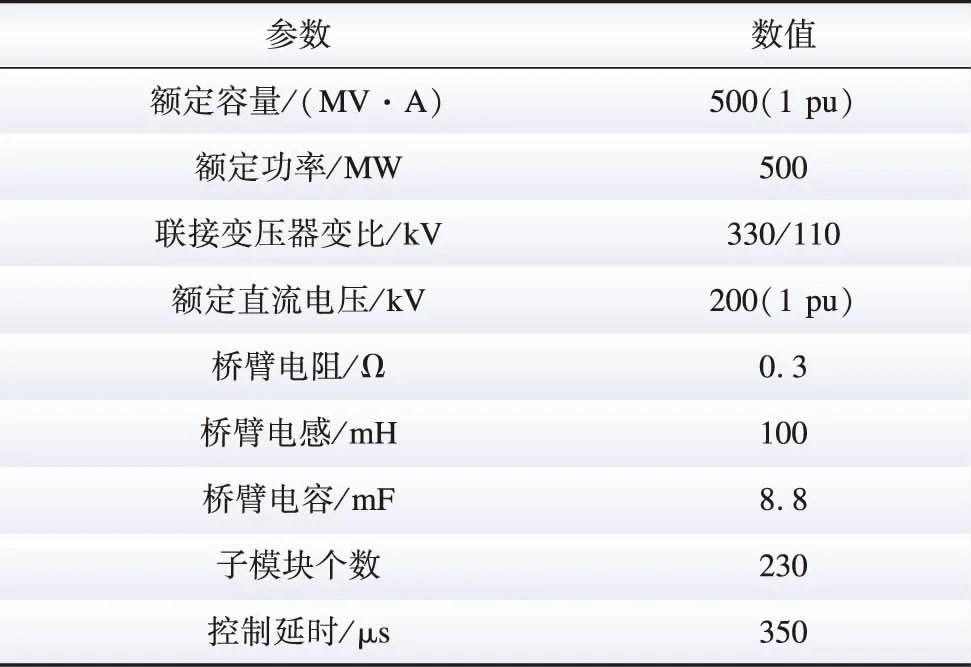
表1 仿真平台主要参数Table 1 Main parameters of simulation platform

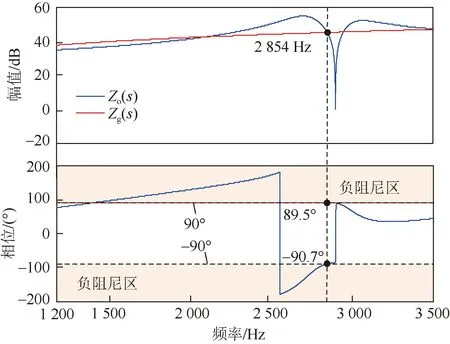
图6 空载线路投入MMC交流侧等效阻抗Bode图Fig.6 Equivalent impedance Bode diagram of MMC AC side for unloaded line input

由图6可知,MMC交流侧等效阻抗在1 427～2 855 Hz频段内为负阻尼,具有发生高频谐振的可能性,并且MMC交流侧等效阻抗与电网侧阻抗在2 854 Hz处存在幅值交点,在频率交接处,其相位差为180.2°,根据稳定性判据可知,柔直系统在该频率附近存在高频谐振风险。

3.2 MMC站间谐振传播路径分析

由于采用均压控制策略,设桥臂子模块(sub-module, SM)电压均相等[33],并且输出的交流电压有相对应的谐波成分,加之考虑二次环流抑制措施,故认为输出的交流电流仅含基波成分[34]。以a相为例,设其电压初相为0°,所以流经MMC上、下桥臂的电压upa、una和电流ipa、ina可表示为:

(4)

(5)

(6)

(7)

式中:Ua1、Uah、Ia1分别为基波电压幅值、h次谐波电压幅值及基波电流幅值;φah、αa1分别为h次谐波电压及基波电流对应的初相位;ω=100π rad/s。由式(4)-(7)可得MMC的a相功率瞬时值表达式为:

(8)

(9)

(10)

(11)

(12)

同理可得到b、c两相的桥臂瞬时功率:

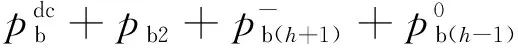
(13)

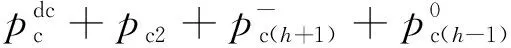
(14)

稳态时,直流分量应为0,否则将会引起SM电容电压上升,导致MMC不稳定;并且功率中的正序分量和负序分量不会流入到直流侧,只有零序分量会经过桥臂进入直流侧,进而导致直流侧出现高频扰动[35]。

由上文可知,当MMC交流侧出现高频谐振时,高频扰动经由桥臂传递到直流侧,引起直流侧电压、电流及功率高频扰动。对于MMC-MTDC系统,直流侧的高频扰动会在直流线路上传播,进而波及到各个MMC。本节重点探究受端MMC3高频谐振能量传播路径及对MMC2和MMC4的影响机理。

对MMC3、MMC2、MMC4的控制器进行联合建模,MMC3发生高频谐振时MMC2、MMC4受谐振影响的控制结构如图7所示。当MMC3交流侧高频谐振时,其直流侧高频扰动h-1次谐波电压ΔUdc(h-1)和h-1次谐波功率ΔP(h-1)分别传递给MMC2和MMC4。考虑到ΔUdc(h-1)和ΔP(h-1)直接影响控制器的有功分量id,于是通过id的变化间接表示ΔUdc(h-1)和ΔP(h-1)对换流器直流侧的影响。

图7 下垂站对直流电压站的高频谐振影响框图Fig.7 Block diagram of high-frequency resonance effect of sag station on DC voltage station

因此MMC2控制器id受ΔUdc(h-1)的影响为:

Δid=H′2ΔU(s)ΔUdc(h-1)

(15)

式中:H′2ΔU(s)为ΔUdc(h-1)对id的扰动传递函数,其开环传递函数H2ΔU(s)为:

(16)

MMC4控制器id受ΔUdc(h-1)和ΔP(h-1)的影响为:

Δid=H′4ΔU(s)ΔUdc(h-1)+H′4ΔP(s)ΔP(h-1)

(17)

式中:H′4ΔU(s)、H′4ΔP(s)分别为ΔUdc(h-1)和ΔP(h-1)对id的扰动传递函数。

H4ΔU(s)和H4ΔP(s)为H′4ΔU(s)和H′4ΔP(s)的开环传递函数,表达式分别为:

(18)

(19)

各扰动开环传递函数Bode图如图8所示。图8中,H2ΔU(s)的剪切频率为34.51 Hz,相位为-99.231°,2 800 Hz处的幅值增益为-38.29 dB,相位为-90.11°;H4ΔP(s)的剪切频率为341.09 Hz,相位为-100.05°,2 800 Hz处的幅值增益为-18.29 dB,相位为-90.11°。2 800 Hz处对应的幅值增益说明在换流站控制器的作用下,虽然高频扰动在传递过程中会有所衰减,但是不能完全消除高频谐波对MMC2和MMC4控制中id的影响;同时,由相位信息可知,MMC2和MMC4对高频扰动响应滞后于MMC3的扰动输出。

图8 开环传递函数Bode图Fig.8 Bode diagram of open-loop transfer function

综上,当MMC3交流侧高频谐振时,其直流侧ΔUdc(h-1)导致MMC2直流侧高频波动,而在ΔUdc(h-1)和ΔP(h-1)的双重作用下,导致MMC4直流侧高频波动。可见,MMC所受高频谐波影响程度还与其外环控制方式有关,由于MMC4受到功率和电压扰动的双重影响,即采用下垂控制的4站比采用直流电压控制的2站受高频扰动影响程度更大,因此MMC4直流侧波动更剧烈。

4 柔直系统高频谐振抑制方法

消除或压缩MMC交流侧等效阻抗高频段的负阻尼区间,是抑制柔直系统MMC高频谐振的必要条件[7]。因此,本文采用电压前馈串联带阻滤波器的高频谐振抑制策略,以改善MMC交流侧等效阻抗在高频段的阻抗特性,以达到抑制高频谐振的目的。含带阻滤波器的MMC简化控制模型如图9所示。

图9 附加带阻滤波器的MMC简化控制模型Fig.9 MMC simplified control model with additional bandstop filter

图9中,Gf为电压前馈串联带阻滤波器环节的传递函数,其表达式为:

(20)

式中:ωc=2πfc,fc为带阻滤波器的中心频率;ξ为阻尼系数。由图9可得,含带阻滤波器的MMC高频简化阻抗为:

(21)

带阻滤波器对MMC交流侧等效阻抗的影响如图10所示。

图10 带阻滤波器对柔直系统阻抗特性的影响Fig.10 Influence of bandstop filter on impedance characteristics of flexible DC system

由图10可知,带阻滤波器中心频率的增加以及阻尼系数的减小都会让MMC交流侧等效阻抗在频率交接处(2 850 Hz)附近远离负阻尼区,从而有利于提高MMC该频率附近的稳定性。但过低的阻尼系数,将导致带阻滤波器调节范围变小,使得谐振抑制的带宽变窄,为了达到良好的谐振抑制效果,故阻尼系数不宜过低[36]。因此,综合考虑带阻滤波器中心频率和阻尼系数对MMC交流侧等效阻抗的影响,选定fc=3 000 Hz,ξ=0.707。图11为采取电压前馈串联带阻滤波器阻抗改善后的MMC交流侧等效阻抗Bode图。

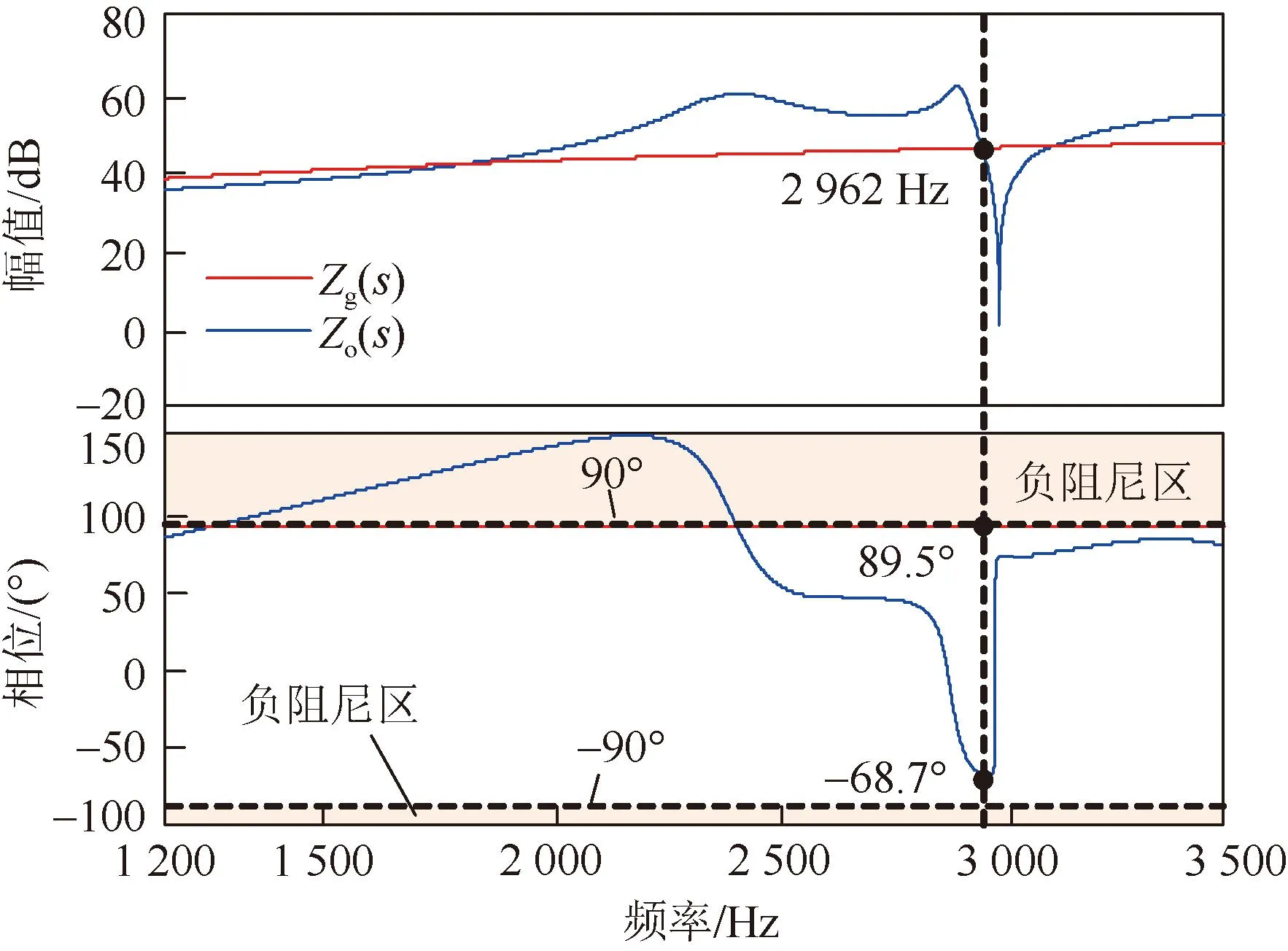
图11 阻抗改善后的MMC交流侧等效阻抗Bode图Fig.11 Equivalent impedance Bode diagram of MMC AC side after impedance improvement

比对图6和图11可知,通过应用电压前馈串联带阻滤波器抑制策略,MMC交流侧等效阻抗特性在较低频段变化较小,但其与交流系统阻抗交接频率由2 854 Hz增大至2 962 Hz,该频率处2个阻抗的相位差由180.2°降至158.2°。可见电压前馈串联带阻滤波器后MMC系统阻抗获得改善,在2 854 Hz附近处于稳定区间。

5 仿真分析

本文在RT-LAB 5600实时在线仿真平台搭建了如图2所示的四端MMC-MTDC系统仿真模型,系统仿真参数如表1所示。其中MMC1采用有功、无功控制(P=1 pu,Q=0 pu),MMC2采用直流电压、无功控制(Udc=1 pu,Q=0 pu),MMC3、4均采用下垂、无功控制(Q=0 pu),直流线路l12=l23=l34=10 km。

5.1 算例1

为了验证第3.1节空载线路投入柔直系统产生高频谐振分析方法及第4节高频谐振抑制策略的正确性,基于5.1节搭建的四端柔直系统进行对应仿真。3.0 s时MMC3交流侧投入空载线路,3.5 s时启用高频谐振抑制策略。图12为MMC3空载线路投入前后并网点三相电压电流波形。由图12可知,在3.0 s空载线路投入后,由于MMC3交流侧等效阻抗与交流系统阻抗在频率交接处相位裕度不足而发生高频谐振,3.5 s启用抑制策略有效抑制了系统高频谐振。

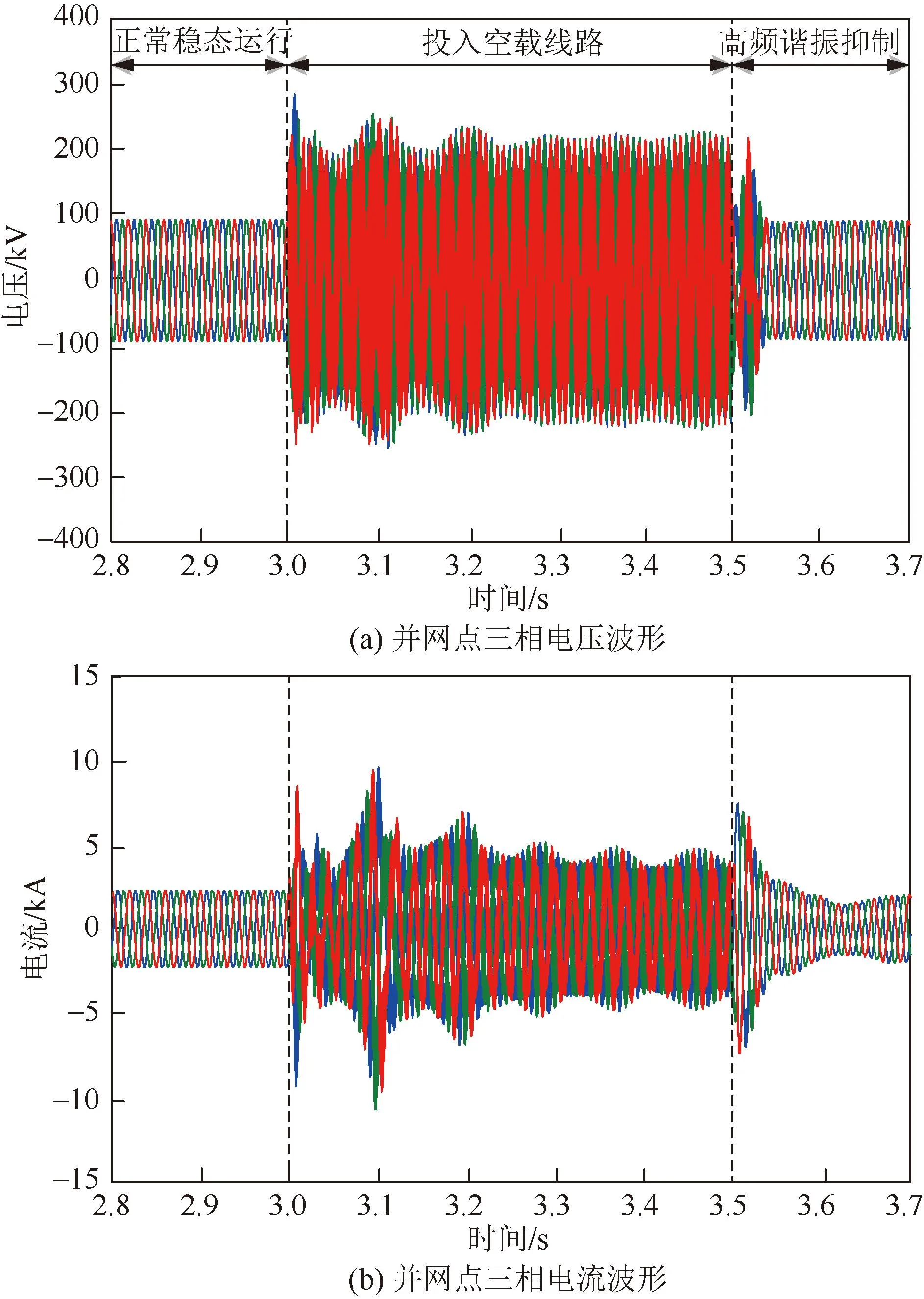
图12 空载线路投入前后并网点电压电流波形Fig.12 Voltage and current waveform of PCC before and after unloaded line input

空载线路投入前后MMC3并网点电压、电流波形及傅里叶分析结果如图13所示。空载线路投入后,MMC3交流侧出现频率为2 850 Hz的高频谐振,与3.1节的理论分析基本吻合。

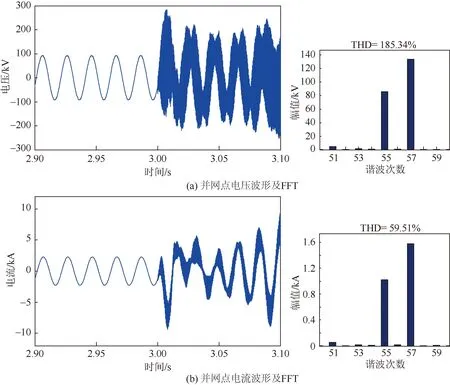
图13 空载线路投入前后仿真波形及FFTFig.13 Simulation waveform and FFT before and after the unloaded line input

由图13可知,还存在一个频率为2 750 Hz的高频谐振点,利用傅里叶分析(fast Fourier transform, FFT)可知,2 850 Hz为正序,2 750 Hz为负序。由于交流侧h次正序谐波会在直流侧产生h-1次零序谐波,而直流侧h-1次零序谐波又会反作用于交流侧产生h-2次负序谐波[22],因此MMC交流侧在原来谐振频率基础上会再出现一个相差100 Hz的频率。故对柔直系统而言,在该谐振条件下,系统的谐振频率主要集中在2 750 Hz和2 850 Hz这2个频率附近。由图13可知,当系统高频谐振出现以后,并网点电压波形畸变率(total harmonic distortion, THD)为185.34%,并网点电流波形畸变率为59.51%。

采用高频谐振抑制策略前后,MMC3并网点电压、电流波形及傅里叶分析结果如图14所示。相较于图13,采取高频谐振抑制策略后,MMC3等效阻抗(与交流系统阻抗)交接频率由2 750、2 850 Hz增至2 850、2 950 Hz,与第4节高频谐振抑制理论分析基本吻合。同时由图14看出,启用抑制策略后并网点的电压电流谐振得到明显抑制,其电压波形畸变率由185.34%下降到0.52%,电流波形畸变率由59.51%下降到0.41%,满足系统运行对电能质量的要求。

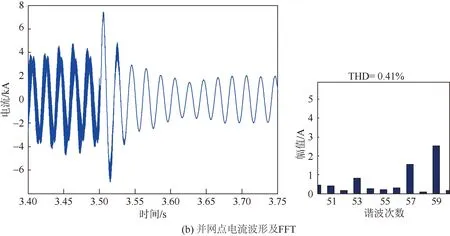
图14 启用高频谐振策略前后的仿真波形及FFTFig.14 Simulation waveform and FFT before and after enabling high-frequency resonance strategy

5.2 算例2

为验证3.2节换流站间高频谐振传播理论分析的正确性,基于5.1节搭建的四端柔直仿真模型,进行高频谐振对受端MMC影响的仿真分析。3 s时MMC3交流侧投入空载线路,柔直系统发生高频谐振,谐振持续时间1 s;4 s时启用高频谐振抑制策略,系统恢复稳定,各站的直流侧电压电流波形如图15所示。图15中,ΔUj、ΔIj(j=1, 2, 3, 4)分别为MMCj(j=1, 2, 3, 4)直流侧的电压、电流波动率。由图15可知,当MMC3交流侧出现高频谐振时,高频扰动会通过MMC3传递到其直流侧,并通过直流线路影响到其他MMC。各MMC直流侧电压电流波动情况如表2。

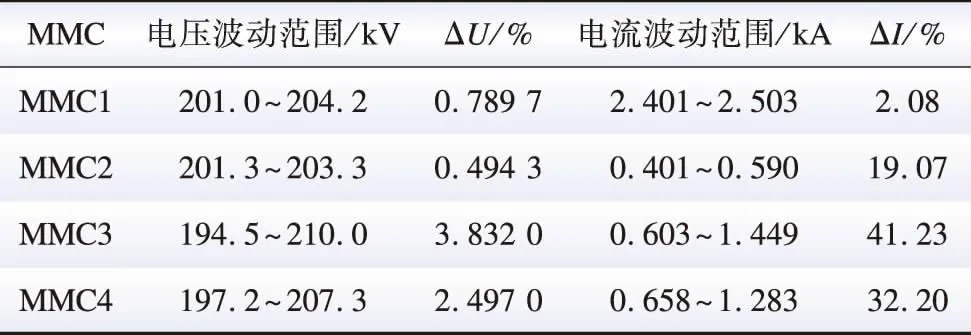
表2 各MMC直流侧电压电流波动Table 2 Voltage and current fluctuations on the DC side of each MMC

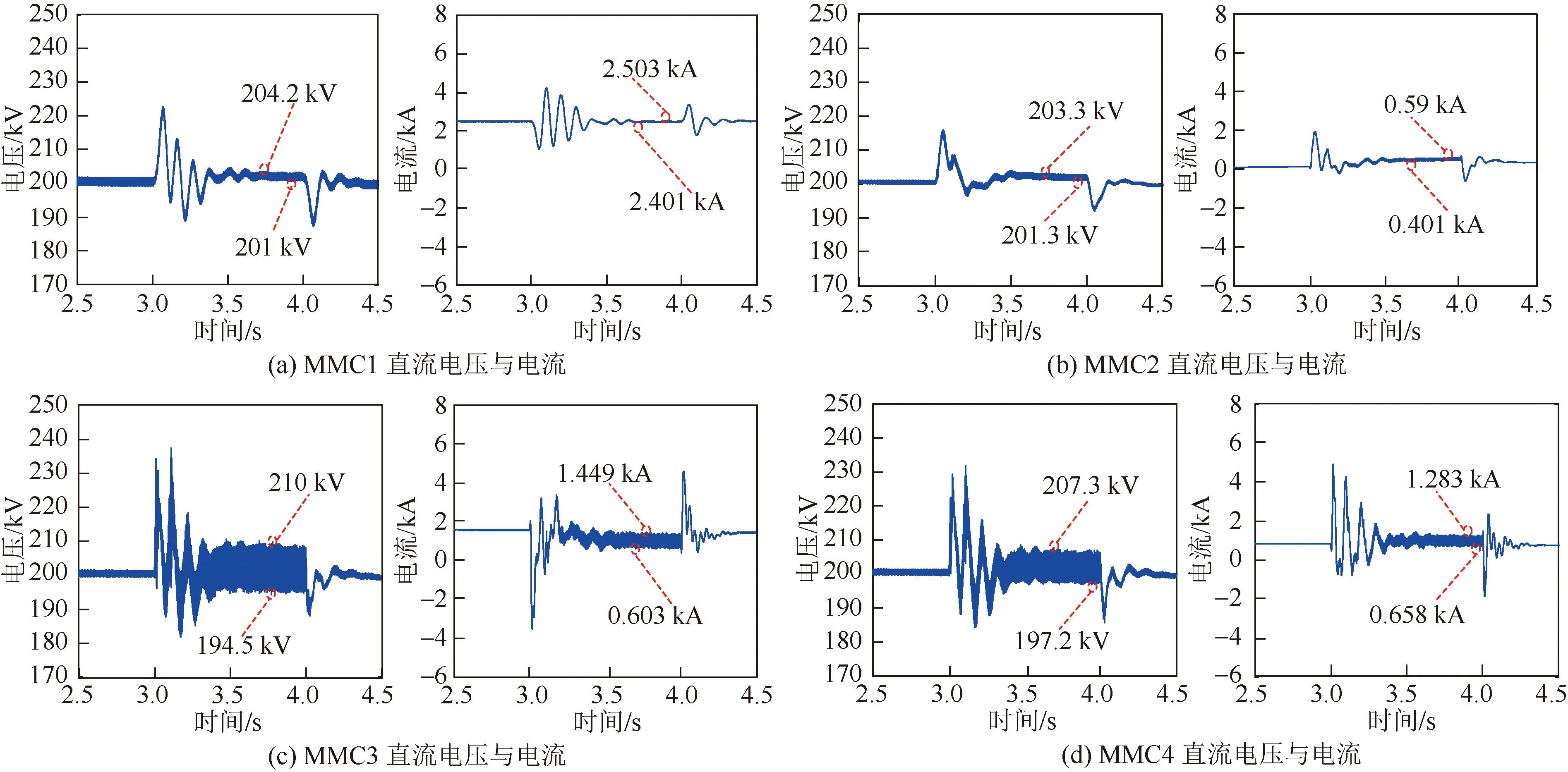
图15 高频谐振时MMC直流侧电压电流仿真波形Fig.15 Simulation waveform of voltage and current on the DC side of MMC during high-frequency resonance

由电流波动率可知,MMC4比MMC2受高频扰动影响程度更大,其电流波动率为MMC2的1.5倍以上。上述仿真结果与3.2节换流站间的高频谐振传播理论分析基本吻合。

6 结 论

本文就多端柔直MMC交流侧空载线路投入引发的MMC高频谐振及站间扰动能量传播问题展开研究。通过理论分析及仿真验证得到如下结论:

1)由于空载线路的投入,导致MMC交流侧等效阻抗在高频段呈负阻尼特性,增加了系统发生高频谐振的风险。

2)MMC交流侧高频谐振不但会传递到直流侧,而且能通过直流线路对其他MMC产生影响,各MMC受高频扰动的影响程度与其外环采用的控制方式有关。

3)电压前馈串带阻滤波器的高频谐振抑制策略能够改变MMC交流侧等效阻抗,消除其在交接频率附近的负阻尼,从而有效抑制系统的高频谐振。