基于定位法线的工件最少定位点布局规划方法

王友利，张铎，王晓慧

（太原科技大学机械工程学院，山西太原 030024）

0 前言

机床夹具设计中，工件定位方案的确定是其首要内容，建立定位点布局在定位方案规划过程中起着承前启后的作用，其不仅决定了定位方案实际限制的自由度，而且对定位基准以及定位元件的选择有一定的参考意义。王晓慧等［1-2］利用定位元件与工件接触点的数量及其几何关系，提出了定位法线几何定理，用于判断定位方案所限制的自由度。陈广锋等［3］利用规则推理与模糊评判的方式，根据工件信息确定定位方案。田韶鹏等［4］利用矩阵表示工件定位点到加工特征关键点处的误差，以矩阵特征值建立目标函数对6 个定位点位置进行优化，从而获取定位点布局。秦国华等［5］将工件定位方案与齐次方程组解的性质相结合，判断定位方案的合理性。吴玉光［6］通过对于基准定位能力的判断，进行定位方案的规划。WU 等［7］利用模糊评判结合遗传算法，实现对于定位点的布局与优化。马杰等人［8］利用有限元方法，引入带有惩罚因子的弹簧接触模型，对定位点布局进行优化。彭贺明、吴玉光［9］利用定位点的数量和布局表示基准约束自由度的能力，从而确定定位方案。秦国华等［10-11］通过定位点处法向量信息，判断定位方案的合理性并对其加以修正。韩霞等人［12］建立了组合定位中各定位元件限制自由度的分析准则，便于进行定位方案的设计与优化。姜坤等人［13］以准确性和定位稳定性为指标，针对3-2-1 约束对移动点连续搜索，从而获取定位点布局。秦国华等［14］建立了保证定位确定性的定位点总体数目条件，进而根据工艺要求确定定位方案。IVANOV 等［15］通过工件的几何参数，确定工件与定位元件之间的空间几何关系，从而得出定位方案。

上述研究中所提出的方法对于工件定位方案规划有着重要作用，但这些方法在规划方案的过程中需进行大量数学运算或使用算法优化，对使用者提出了较高的要求，在企业中大范围推广的难度较大。因此，一种简单、易行，且能够针对工序需求自由度规划定位点初始布局的方法，对于定位点布局建立的合理与否起着至关重要的作用。

本文作者以实现最少定位点限制工序所需限制自由度为目标，以定位法线数量及其几何关系的几何定理为依据，建立定位法线与自由度约束的关系模型，由此规划工件定位方案，从而建立工件最少定位点初始布局。

1 自由度约束与定位法线的关系

1.1 定位法线概述［1］

定位法线是指工件与定位元件接触点处的法线，如图1（a）所示，而定位法面则是由两条或多条处于同一平面的定位法线组成，如图1（b）所示。

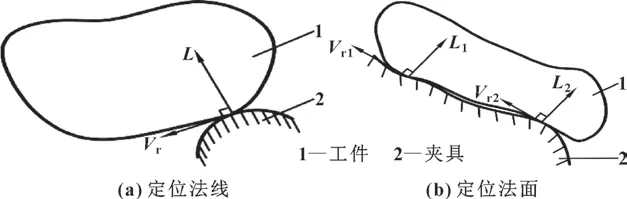
图1 定位法线原理Fig.1 Principle of location normal：（a）location normal line；（b）location normal plane

定位法线几何定理，用于确定法线能够限制的自由度：

定理1 一条法线能限制此法线方向的移动自由度；

定理2 两条同方向法线组成的定位法面，能限制该法面垂线方向的转动自由度与法线方向的移动自由度；

定理3 3 条同方向且不共面法线，可以组成2个定位法面，能限制2 个法面各自垂线方向的转动自由度与法线方向的移动自由度。

1.2 定位法线表示方式

本文作者将定位法线用字母L加下标的方式表示，其中下标为字母u、v和w，表示笛卡尔坐标系的3 个方向；定位法面用字母P加下标的方式表示，其中下标为字母uv、uw和vw，表示空间坐标系中3个相互正交的平面；若某一方向有两条或者多条定位法线，则用定位法线加定位法面的组合表示，如LvPvw表示vw平面上v方向的法线。

1.3 自由度需求的定位法线数量及方向的确定

由工件定位的几何定理可以得出推论，用于确定限制工件自由度所需的法线数量及其方向。

推论1 单移动自由度：若需限制工件某一个方向的移动自由度，所需定位法线数量为1 条，且法线方向为该移动自由度方向。

推论2 转动自由度：（1）若需限制工件某一个方向的转动自由度，所需定位法线数量为2 条，且2条法线的起点连成的直线与该转动自由度方向垂直；（2）若需同时限制工件在一个平面内的2 个转动自由度，只需在限制其中一个转动自由度所需法线方向添加1 条法线，3 条法线不共面，且3 条法线的起点在该平面内。

结合推论1 和推论2 可知，限制工件某一方向转动自由度的2 条法线或限制平面内的2 个转动自由度的3 条法线必限制了法线方向的移动自由度。

推论3 单移动与转动自由度组合：（1）若需限制工件某一个方向的移动自由度和转动自由度，所需定位法线数量为2 条，且2 条法线的起点连成的直线与该转动自由度方向垂直；（2）若需限制工件某一个方向的移动自由度和与其正交的2 个转动自由度，则需要3 条与移动自由度同方向的不共面法线，且3条法线的起点在该平面内。

由推论可知限制转动自由度所需的定位法线信息如表1 所示。

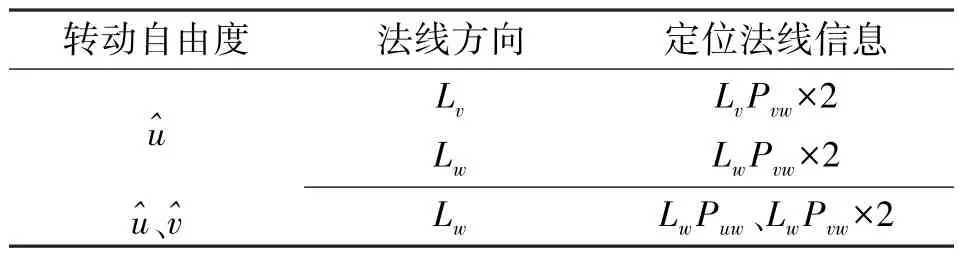
表1 限制转动自由度的定位法线信息Tab.1 The location normal information with limiting the rotational freedom

2 定位法线规划

2.1 设计过程

将工件加工时需要限制的自由度采用矩阵形式表达，矩阵的第一行元素代表自由度的类型及方向，第二行元素为其对应的值，该数值类型为布尔型，采用b加下标字母表示，下标字母与第一行元素相对应。当工件加工要求需限制某一自由度时，bi＝1，此自由度称为真值元素，否则bi＝0，称为非真值元素。按照上述自由度模型的表达方式，工件加工要求应限制自由度数学模型为

工件定位点布局的定位法线布置过程如下：

第一步，从自由度模型中获取移动自由度数学模型：

第二步，从自由度模型中获取转动自由度数学模型：

第三步，为规划最少定位点布局，定义一种逻辑减运算：

运算法则如表2 所示。

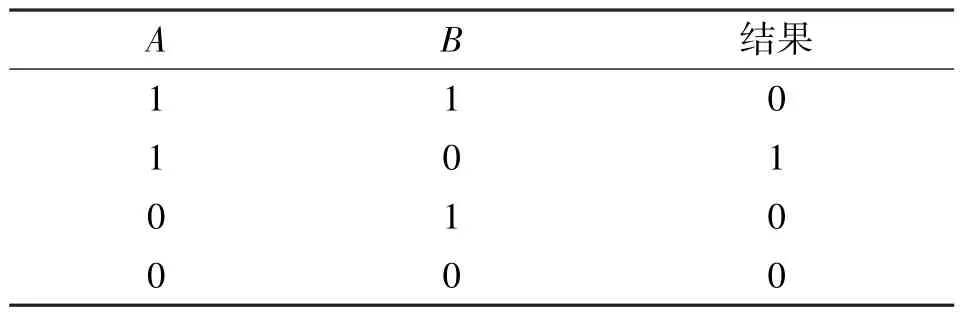
表2 逻辑减运算法则Tab.2 The logical subtraction algorithm

第四步，确定定位法线数量及方向。

定位法线数量和方向的确定规则及过程如下：

使用字母N加下标的方式表示自由度模型中真值元素的个数，下标为δi（i＝r、s、t），表示不同类型的自由度模型，判断Nδs、Nδt、Nδr执行对应操作：

（1）若δr＝0，只需限制移动自由度，为δt中的真值元素提供一条对应的法线，定位法线规划结束。

（2）若Nδr≠0 但Nδs＝0 时，需要限制同一个方向的转动自由度和移动自由度，根据表1，依次利用δt中真值元素为δr中的真值元素提供对应的法线，直到为δr中的真值元素提供全部的法线，获得法线的数量和方向，定位法线规划结束。

（3）若Nδr≠0 且Nδs≠0 时，需要限制的移动自由度与转动自由度不全相同，根据表1，依次利用δs中真值元素为δr中的真值元素提供对应的法线，并提供δt中真值元素对应的法线，直到为δr和δt中的真值元素提供全部的法线后结束，获得法线的数量和方向，定位法线规划结束。

2.2 定位法线规划结果

以第2.1 节的最少定位点布局规划过程可以得到不同自由度模型的定位法线信息如表3 所示。

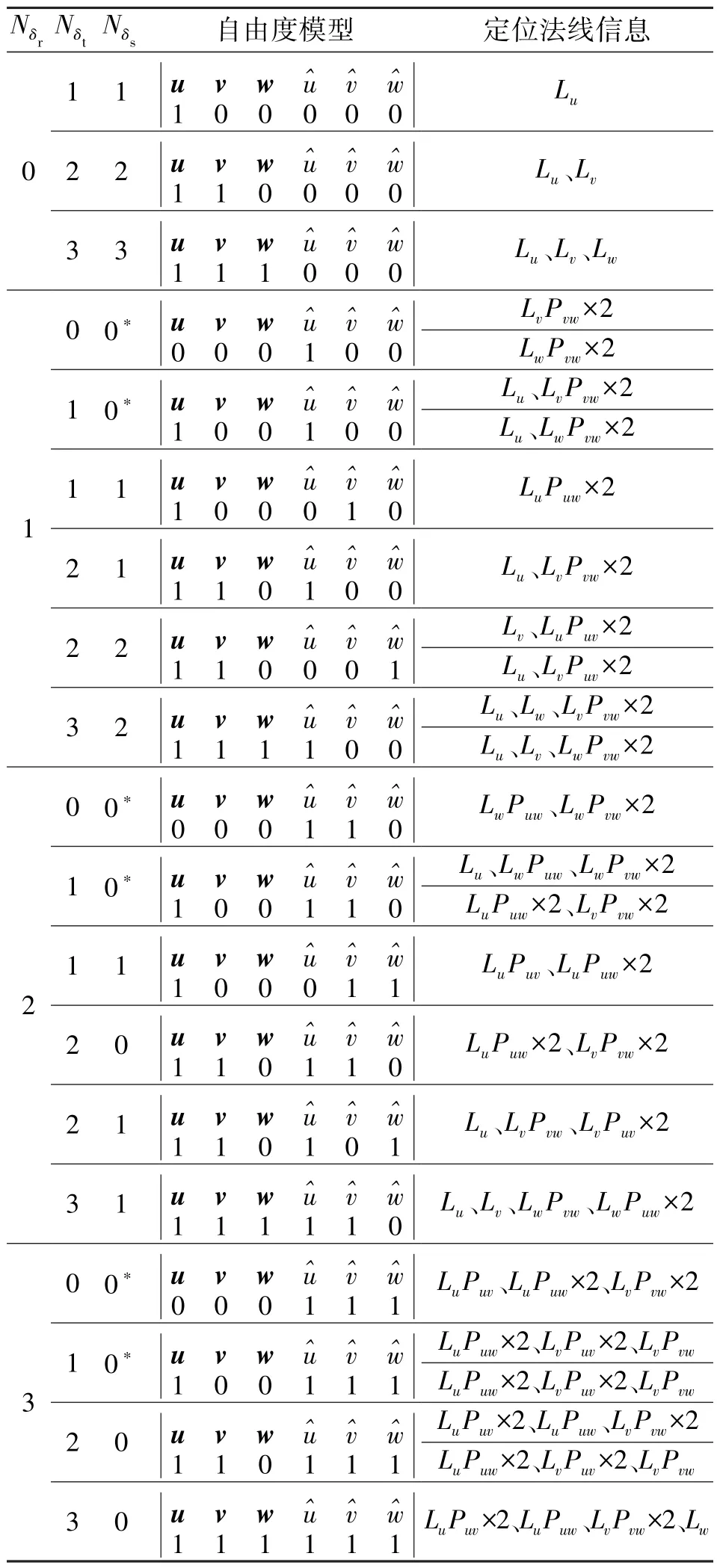
表3 不同类型自由度模型定位法线信息Tab.3 The location normal information with different types of degrees of freedom model

3 定位点初始布局与定位法线的关系

定位点初始布局包含：（1）定位点所处表面信息；（2）同一表面上多个定位点的位置关系。依据定位法线信息得出定位点布局的方式如下所示：

（1）搜索定位点所在表面

定位法线代表的定位点位于正交于此法线的表面上，根据定位法线的方向，可以确定该法线代表的定位所在表面的坐标系信息。确定一个表面后，在定位法线集合中减去此表面所提供的定位法线，依据剩余的定位法线信息搜索下一表面。重复上述操作，直至定位法线集合为空，定位点所在表面搜索完毕。

（2）获取同一表面上多个定位点位置关系

一个表面有多条定位法线时，定位法面表示同一平面内定位点的位置关系。如2 条定位法线Lv组成的定位法面Puv，3 条定位法线Lw组成的2 个定位法面Puw、Pvw，可以得到定位点布局如图2 所示。需要注意的是，当3 条同一方向的法线组合为2 个法面时，定位点布局并不要求2 个法面正交，只需确保3条法线不在同一平面即可。

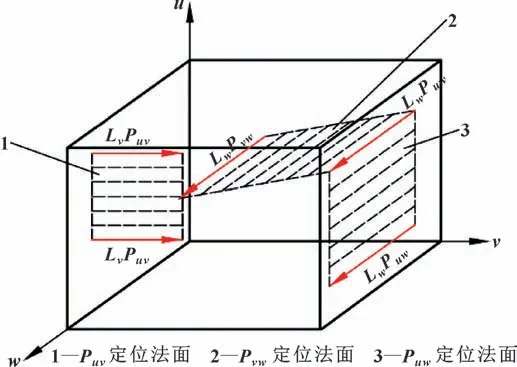
图2 根据定位法线信息确定的定位点布局Fig.2 Location points layout determined by location normal information

4 实例分析

图3 为某工件加工简图，工件上的ϕ16 mm 通孔为待加工表面，通过工序需求限制的自由度，获取自由度数学模型

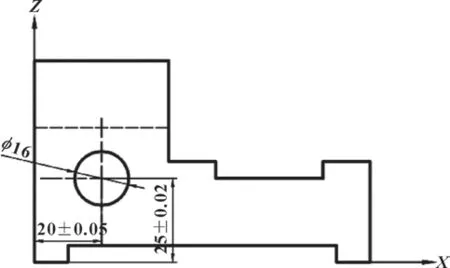
图3 工件加工工序简图Fig.3 Workpiece processing process diagram

对δt、δr进行逻辑减运算

根据自由度模型可得：Nδt＝2，Nδr＝3，Nδs＝0，依据表4 可知此自由度模型的定位点布局有两种方式，定位法线信息为

（1）LuPuv×2、LuPuw、LvPvw×2；

（2）LuPuw×2、LvPuv×2、LvPvw。

按照表1 备注中的方式对下标进行转换：u为模型中第一个真值元素，若u＝x，则δt中的另一个真值元素v＝z，剩余元素w＝y，可得定位法线信息为

（1）LxPxz×2、LxPxy、LzPyz×2；

（2）LxPxy×2、LzPxz×2、LzPyz。

根据定位法线信息获取定位点布局：

两套定位方案中，定位法线的方向均为x、z，首先根据Lx法线确定第一个定位表面，与x方向正交的平面为Pyz，则Lx法线所处平面为Pyz，在定位法线信息中删除该表面所提供的法线。剩余法线信息为Lz，与z方向正交的平面为Pxy，则Lz法线位于Pxy平面，第二个定位表面确定，此时定位法线信息集合为空，定位表面的坐标系信息搜索完毕。根据法面信息可得定位点位置关系。

由于定位法线信息仅提供了定位点所在表面的坐标系信息，而此工件中与Pxy、Pyz平面平行的表面不止一个，所以结合定位基准优选方式，在平行于Pxy或Pyz的所有平面中选择定位基准，根据基准重合原则，平行于Pxy平面的工件底面、平行于Pyz的工件左侧表面，均与待加工特征有公差要求，故选择这两个表面作为定位基准。图4 为搜索定位表面及获取定位点布局的过程与结果。

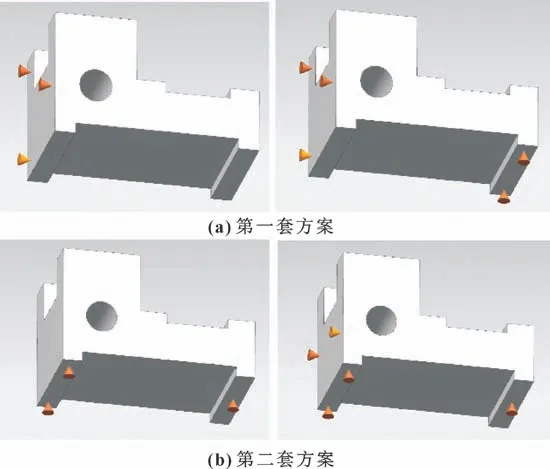
图4 定位方案规划Fig.4 Locating schemes planning：（a）the first set of scheme；（b）the second set of scheme

第一套定位点布局在Pxy平面上布置2 个定位点，第二套定位方案中在Pxy平面上布置3 个定位点。由于Pxy为工件底面，在实际生产过程中，底面布置2个定位点，即将底面作为第二基准，并不能保证工件的稳定性，且待加工特征与底面有公差要求，从定位的稳定性以及减小定位误差两方面考虑，都应将底面作为定位点数量最多的表面，即第一基准，故选用第二套定位点布局。

5 结语

将工序需求限制自由度采用矩阵形式表达，通过逻辑减运算法则建立工件的自由度与移动自由度和转动自由度的关系，以此关系为准则对自由度模型分类；基于定位法线的工件定位的几何定理，推论出工件自由度与定位法线的集合关系，以此为基础得出定位法线的布置方式。文中定位点布局是基于工序需求限制自由度建立的，每个定位点都承担了限制工序需求自由度的任务，因此是最少定位点布局。

文中的定位点初始布局是基于定位法线信息获取的，此方式提供的定位点所在表面为坐标系信息，而不是某一个具体的表面。若工件在此方向存在多个平行的表面，或存在外圆柱面、孔等非平面特征，则需要通过文中所得出的结果作为参考，缩小定位基准的选择范围，通过定位基准优选的方式，实现定位基准与定位点布局的并行设计，从而获得具体的定位点布局，这也是下一步研究的方向。