基于冲击的涡扇发动机退化建模与下发预测

赵洪利，王之强，张青

（中国民航大学航空工程学院，天津 300300）

0 前言

现代涡扇发动机是具有复杂系统的大型设备，结构复杂，在整个运行期间可靠性维修性要求高［1］。在工程实践中，依靠单一参数快速准确判断发动机退化趋势，并依此对发动机后续地面诊断与维护提供技术支持，是较为重要的研究课题。

作为可靠性数学理论中的一种，基于冲击模型的设备可靠度分析与剩余寿命预测得到了较为广泛的应用。常见冲击模型一般有5 种：累计冲击模型［2］、极端冲击模型［2］、连续冲击模型［3］与后两者的混合冲击模型［4］以及较新的δ 冲击模型［5］。YUAN 等［6］对冲击与退化概率失效阈值不确定情况下的k／n系统进行了研究，并选取两种算例进行对比。王强等人［7］也做了类似研究。KEEDY、FENG［8］提出包含混合冲击模型的可靠性退化模型，使用MEMS 器件进行验证，得到了其退化度。KONG 等［9］针对复杂装备失效过程实施连续检测手段，并利用传感器的退化数据进行校准，推导出系统的可靠性退化函数。AN、SUN［10］提出高可靠性产品具有抵抗小型冲击的能力，假设在一定阈值内冲击会使性能退化，当超过某一阈值时系统故障，在此基础上建立了微型发动机的可靠性退化模型。JIANG 等［11］考虑产品受退化和随机冲击作用，并考虑突发失效阈值降低的情况，建立了产品可靠性退化模型。SONG 等［12］研究了具有多个零部件的复杂系统，考虑每个零部件都经受退化和冲击导致的多个失效过程，由此推导出系统可靠性退化模型。陈童等人［13］假设退化与冲击采用不同的维修方式，利用PH分布与更新过程研究多状态冷贮备系统可靠性退化规律。潘刚等人［14］针对高可靠部件难以获取性能分布信息的问题，提出了竞争失效下基于认知不确定性的多态系统可靠性评估方法，并利用算例验证了模型的有效性。王浩伟等［15］为解决某型导弹部件的贮存寿命预测问题，提出一种随机环境应力冲击下基于多参数退化的寿命预测方法。上述研究显示冲击模型具有良好的理论价值与工程适用性，可依靠单参数对设备进行可靠性分析与剩余寿命预测且结果良好；对于涡扇发动机等大型设备的单性能参数退化分析具有良好的应用前景。

涡扇发动机常用发动机排气温度裕度（Exhaust Gas Temperature Margin，EGTM）的衰退表示起飞时性能退化程度，EGTM 定义为发动机排气温度（Exhaust Gas Temperature，EGT）红线值与海平面拐点温度下全功率起飞时EGT 差值［1］，主要用于反映发动机的性能衰退情况，是最重要的性能监测数据。对EGTM 变化规律的研究，一直是航空公司重要课题；掌握其退化规律可以更好地预测发动机在翼时间，管理发动机大修计划以及备发准备等，对于降低航空公司的运营成本，具有实际的意义。王华伟等［16］借助竞争失效理论，将常规失效分为退化失效与突变失效，借由贝叶斯线性模型融合EGTM 退化数据与其他非同源退化数据用于描述退化失效，使用故障信息建立混合Weibull 可靠性模型用于描述突变失效，由此求解出航空发动机的剩余寿命。王大伟等［17］采用模糊积分结合故障强度因子融合各可靠性参数，解决航空发动机性能动态评估问题。王新刚等［18］结合竞争失效模型，使用Copula 函数与马尔科夫链描述退化过程，引入Weibull 分布与比例标准模型描述突变，构建了航空发动机退化模型。朱磊等人［19］使用Wiener 过程与贝叶斯融合对民用航空发动机进行寿命预测，得到较为合理的寿命预测值。上述学者借用参数融合方法结合常见数学模型描述多参数下发动机退化过程并进行寿命预测，但无法准确描述不同起飞推力下发动机的退化规律。而单一参数虽可以描述不同推力下的退化规律但其准确率较低，无法为后续运行与维护提供技术支持。

为解决上述问题，本文作者提出利用单一参数结合冲击模型来解决发动机性能退化问题。利用某航空公司A321 机队V2500 发动机全寿命EGTM 数据建立其性能可靠度模型。利用非完整EGTM 数据进行下发时间预测，并与真实下发时间对比，表明模型具有较高的拟合精度，能较好地模拟出该机队V2500 发动机衰退规律。

1 模型建立

现代民机起飞有两种选择，以额定最大起飞推力（全功率）起飞和减推力起飞。减推力起飞能降低发动机最大排气温度，延长热端部件在翼时间，延缓发动机退化，是现代涡扇发动机常用的一种手段，但为了保障发动机有全功率起飞能力，适航部门要求定期使用全功率起飞。因此，本文作者在建模时，把日常减推力起飞引起的退化看作自然退化，而全功率起飞由于排气温度最大，热端部件承担大量热载荷，热冲击明显，把其看作极端冲击过程。由于同型发动机具有相同的最大额定起飞推力，因此可近似认为其冲击到达强度相同，具体模拟过程如图1 所示：其中m为冲击次数，nFC为飞行循环数，X（t）表示退化过程，Y表示性能退化量。图1（a）描述退化过程，此过程包含有两个方面：一是自然退化量，二是由随机冲击导致的性能退化累计量，这二者构成了总EGTM 退化量；图1（b）描述上述随机冲击过程；当总退化量超过退化失效阈值H时，即性能可靠度趋降为0，发动机下发。

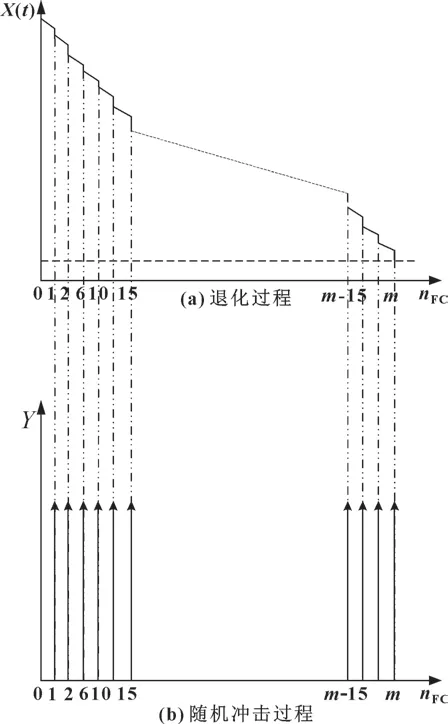
图1 模型示意Fig.1 Schematic of modeling：（a）degradation process；（b）random shock process

1.1 退化模型

假设系统总退化量为

式中：Xs（t）表示EGTM 总 退化 量；X（t）表 示EGTM 自然退化量；S（t）表示随机冲击过程对于自然退化量的增量。各表示为

式中：φ表示初始EGTM 值；β为退化速率；Yi为冲击对系统退化的增量；N（t）为产品受到的冲击次数。

累计退化量为

使用期间产品冲击次数N（t）为一个随机变量，泊松过程是一种重要的点过程，可用来表征随机冲击这种单事件效应；泊松过程具有无记忆属性，也即冲击是随机发生的。在此将整个运行过程中的冲击看作为冲击强度λ的泊松随机过程，则发动机在运行时间t内受到冲击i次可以认为是齐次泊松过程，对应的概率分布为

为估计参数λ，使用引理［20］：设Tn为第n-1 次出现A 事件和第n次出现A 事件的时间间隔，则Tn具有独立的同分布的概率密度与期望为

1.2 性能可靠度计算

由上述假设，随机冲击与自然退化不相独立，性能可靠度建模应遵循条件概率模型，则发动机性能可靠度函数计算式可表达为

第一种情况：在运行期间，N（t）＝0，此时发动机性能可靠度不为0 的概率为R1（t），代入公式（1）可得：

第二种情况：在使用期间，N（t）＝m，其性能可靠度不为0 的概率为R2（t），代入公式（1）可得：

则发动机的总性能可靠度函数为

2 参数估计

表1 为某航空公司A321 机队的V2500 发动机实际运行过程中的全寿命EGTM 数据，这套数据包含从装机直至下发的所有EGTM 数据。

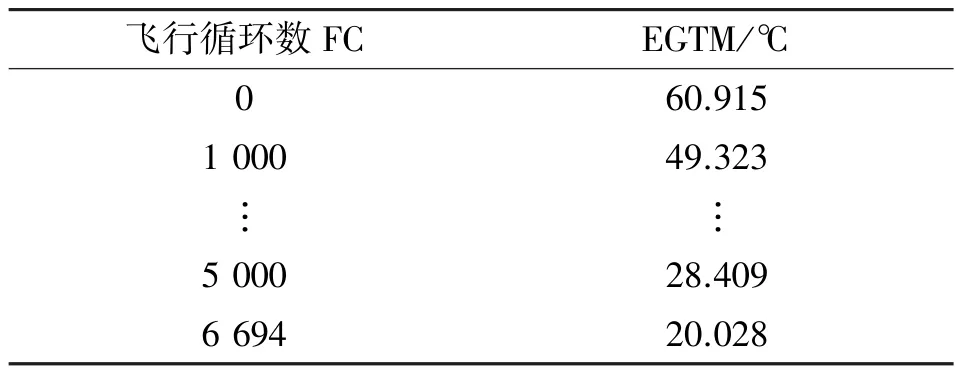
表1 EGTM 数据Tab.1 EGTM datas

由于发动机水洗可消除沉积物累积对发动机性能的影响，所以水洗后，EGTM 会有一定的恢复，因此这部分并不真正代表发动机退化。文中采用中值滤波算法降噪，消除水洗导致的波动点，处理后如图2 所示。

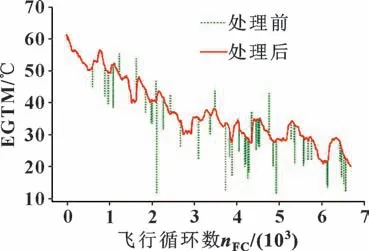
图2 EGTM 数据处理前后对比Fig.2 Comparison of data before and after processing

根据发动机的实际使用情况，对数据进行拟合优度检验。数据量大于5 000，选择进行置信度为95%的Kolmogorov-Smirnov（K-S）检验。K-S 检验属于拟合优度检验，适用于任何连续分布函数，此数据检验P值为0.121＞0.05，通过检验，表明其符合正态分布，上述建模可行。

xi表示第i个飞行循环时的EGTM 数据，冲击次数为m，则对数似然函数为

式（14）与式（15）为超越方程无实数解。这里选择对降噪后的数据使用线性回归分析，假设此时无冲击只有自然退化，基于最大似然函数得到μβ、的公式为

利用处理前数据并取每千次循环为一基准，由式（6）、式（7）、式（14）—（17）进行参数计算，得到上述模型相关参数的值，取值保留小数点后4位。基于上述计算与假设，模型中相关参数的取值参见表2。

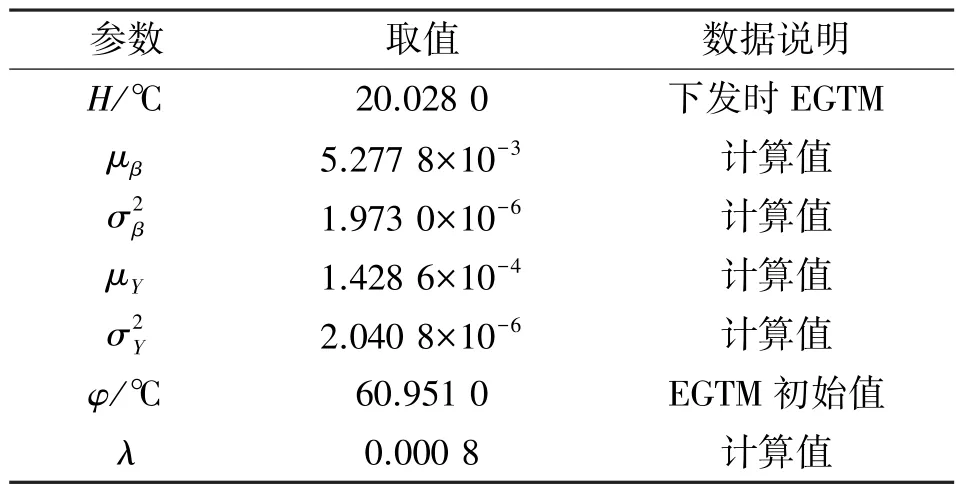
表2 相关参数Tab.2 Related parameters

3 结果分析

将表2 中参数取值代入式（9）—（11）中，得到性能可靠度曲线如图3 所示。

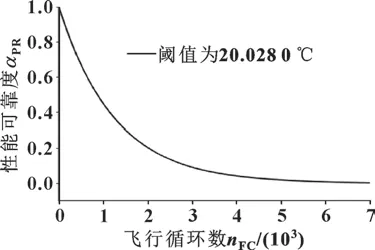
图3 性能可靠度Fig.3 Performance reliability

图3 为退化阈值为20.028 0 ℃时的性能可靠度曲线，可见在前1 000 飞行循环性能可靠度曲线下降较快，在3 000 左右达到一个较平稳的值，之后进入缓慢衰退期直至下发。由图3 可知，基于上述模型的性能可靠度曲线较符合发动机实际性能退化过程。

图4（a）与（b）分别为在2 000～2 100 飞行循环之间与4 300～4 400 飞行循环之间不同阈值对性能可靠性的影响，显示了不同退化阈值时的性能可靠度曲线，表明EGTM 下降速率较快的阶段（飞行循环前期），由于EGTM 下降速率较快使得不同阈值对性能可靠度的影响并不显著；但在可靠度下降速率较慢的中后期，由于下降速率减缓，此时退化阈值对性能可靠度的影响逐渐显现，较大的阈值会加快性能可靠度的下降速率，造成发动机过早下发，较符合实际。

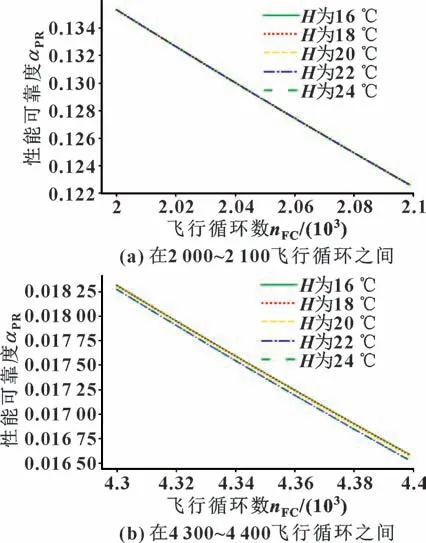
图4 退化阈值灵敏度分析Fig.4 Sensitivity analysis of degradation threshold：（a）flight cycles between 2 000 and 2 100；（b）flight cycles between 4 300 and 4 400

图5 与图6 显示了不同冲击到达强度对发动机性能可靠度的影响。可以看出：曲线的变化速率随冲击到达强度的增大而增大，随冲击到达强度的减小而减小。这是由于冲击到达强度增大表明发动机在同一运行区间内受到冲击次数增多，使得冲击带来的累计损伤量变大，即总退化量增多，反之亦然。图6 表明较大的冲击到达强度在飞行循环前期导致性能可靠度曲线变化速率较快，但在飞行循环后期，这种影响降低。

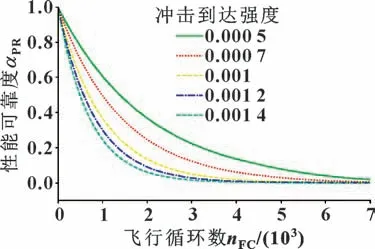
图5 不同冲击到达强度下性能可靠度曲线Fig.5 Performance reliability curves at different impact arrival

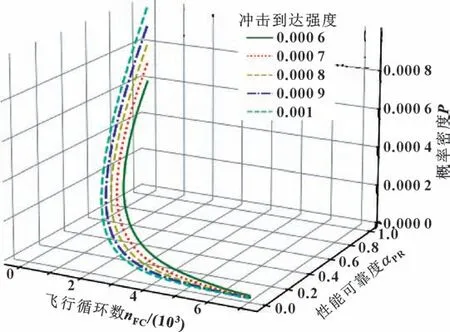
图6 不同冲击到达强度下性能可靠度曲线的概率密度Fig.6 Probability density of performance reliability at different impact arrival

基于以上分析结合参数选取可知表2 计算值较合理。

4 基于性能可靠度的下发时间预测

表3 为上述A321 机队中另外9 台V2500 发动机的非完整EGTM 数据。对表3 中数据同样采用中值滤波算法进行处理，图7（a）—（i）显示此套数据下不同发动机处理数据的前后对比。

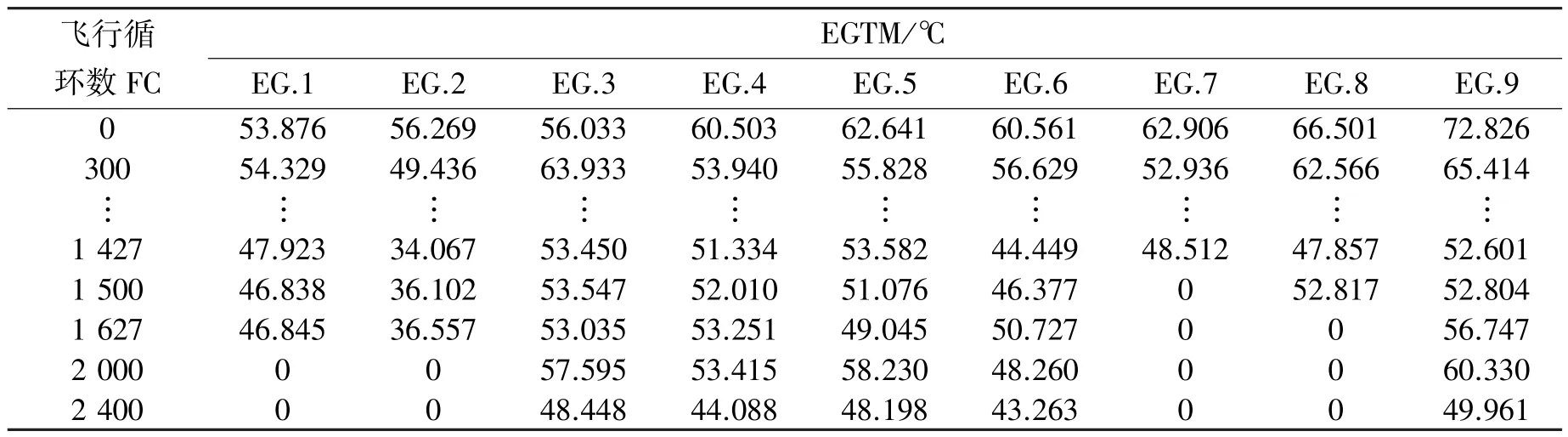
表3 不完整EGTM 数据Tab.3 Incomplete EGTM data

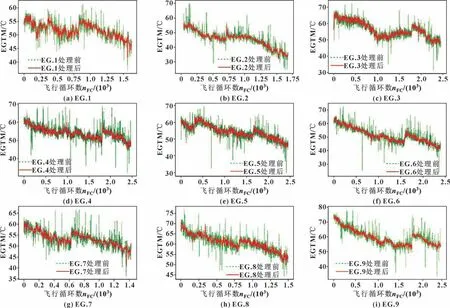
图7 数据处理前后对比Fig.7 Comparison results before and after data processing：（a）EG.1；（b）EG.2；（c）EG.3；（d）EG.4；（e）EG.5；（f）EG.6；（g）EG.7；（h）EG.8；（i）EG.9

由于数据量小于5 000，采用S-W 检验，检验结果如表4 所示。表4 表明各套数据P值均大于0.05，通过了S-W 检验，可用上述模型建模。

表4 S-W 检验结果Tab.4 S-W test results

采用式（14）—（17）结合图7 处理后数据，即可计算得到各台发动机的相关退化参数，结果见表5，参数取值保留小数点后4 位。

表5 各台发动机退化参数值Tab.5 Degraded parameter values of each engine

将上述退化与冲击到达强度代入式（9）—（11）中，得到当性能可靠度为0（结合实际情况选择0.001）时的下发时间，与实际下发时间对比得到误差率，结果见表6。误差率e的计算公式为

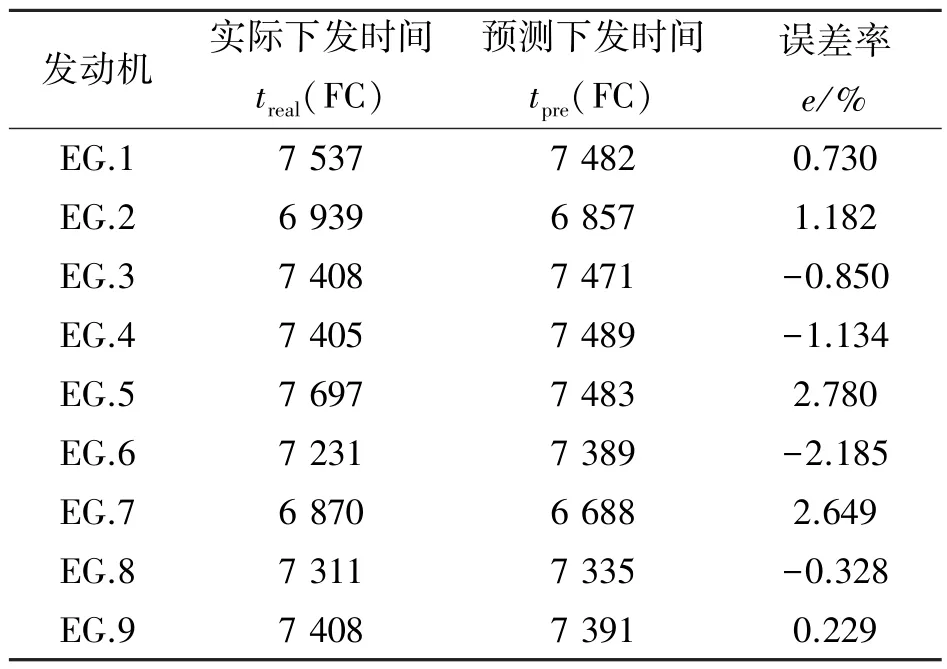
表6 预测结果Tab.6 Forecast results

由表6 可知：误差率在-2%～3%之间，验证了此模型的有效性。

5 结论

为了描述全功率起飞时高燃气温度对发动机退化影响，本文作者基于发动机性能参数EGTM，利用冲击模型建立了发动机性能退化模型，并利用V2500发动机实际EGTM 数据对模型进行验证。结果表明：此模型能够很好地描述热冲击现象，准确预测发动机的下发时间，具有良好的工程应用性。但由于此模型只考虑热冲击这一种情况，对于其他故障的影响分析是接下来的研究重点。