基于椭球体建模的多机器人碰撞检测方法研究

许晓群，侯忠平，王昌顺，杜能，夏卫生

（1.湖北中烟工业有限责任公司武汉卷烟厂，湖北武汉 430040；2.华中科技大学材料科学与工程学院，湖北武汉 430074）

0 前言

多机器人是在一个共同的工作空间中协作运行，彼此之间存在交互和运动，在此过程中就不可避免地会碰撞，一旦发生碰撞就会造成严重的操作事故，甚至严重毁坏机器人的结构，所以系统必须实时检测到这些机器人之间的碰撞。碰撞检测是多机器人协同工作中必不可少的环节和安全工作的保障条件。共享空间的多个几何物体之间分别存在以下3 种位置关系：分离、接触、穿透。碰撞检测是对几何物体之间的位置关系进行实时判断以检测出是否发生接触或穿透现象，并向系统返回其发生的部位［1-2］。所以，碰撞检测技术需要至少三大信息输出：是否碰撞、碰撞部位以及查询距离［3-5］。

碰撞检测是分别对两两物体的空间位置进行检测，多机器人之间的碰撞检测也是基于两两机器人之间的碰撞检测。但机器人的结构不是简单的几何模型，直接进行碰撞检测需要消耗大量的计算成本，所以在对复杂几何结构进行碰撞检测前，通常先执行物体的包围体测试［6-9］。常采用常见的简单几何体去近似替代机器人的机械臂、末端执行器等，从而得到更简略且高效的碰撞检测算法，可以快速且实时地进行多机器人碰撞检测。有些学者用球体代替机器人关节，也有学者将球体平分，中间用圆柱体相连的胶囊体结构代替机器人关节和连杆［10-14］。用于机器人关节与末端表示的主要简化建模方法有长方体表示法、圆柱加半球表示法、球体群表示法和椭球表示法。机器人简化建模和距离计算是相互关联的，每一种包围盒技术都有与之对应的碰撞检测和距离计算算法。用球体对机器人末端执行器进行简化建模，不仅可以紧密包围，而且数学等式简单，并且球体表示不需要考虑方向变化，只考虑位置关系就可以，只有点-点距离计算，计算量最小。用椭球对机器人关节连杆进行逼近，相比单个球体的逼近，不仅对机器人连杆包围更加紧密，而且节约了大量空间［15］。本文作者采用椭球体直接对机器人连杆和关节进行简化建模，从而进行基于椭球体的包围体碰撞检测。

1 基于包围椭球的机器人建模

本文作者基于六自由度工业机器人PUMA560 进行研究。PUMA560 机器人的三维示意如图1 所示，其连杆和关节具体结构如图2 所示。PUMA560 是关节型机器人，含有6 个连杆和6 个关节，6 个运动关节均为转动关节，其末端手腕的运动决定于6 个运动关节顺序运动或同时运动，其中前3 个运动关节确定末端手腕的空间位置，后3 个运动关节确定末端手腕的空间姿态。

图1 PUMA560 机器人三维图Fig.1 3D model of PUMA560 robot

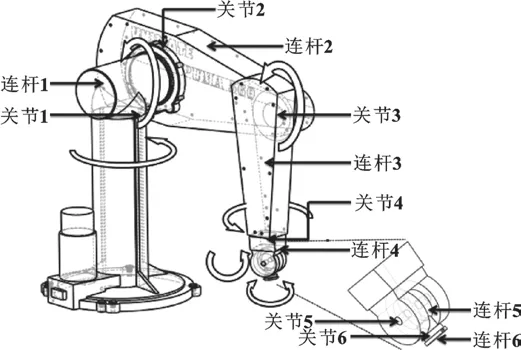
图2 PUMA560 机器人的连杆和关节结构Fig.2 Linkage and joint structure of PUMA560 robot

PUMA560 机器人连杆和关节结构均为不规则几何图形，并且机器人的碰撞检测中反馈的分离距离是机器人的空间位置最短距离，只与机器人前3 个运动关节有关，于是将PUMA560 机器人简化为如图3 所示的三自由度连杆结构。因此本文作者采用椭球体对PUMA560 机器人的三自由度连杆结构进行包围，如图4 所示。由于机器人的碰撞检测在于判断末端结构的碰撞情况，所以主要判断机器人末端包围椭球体的碰撞情况。

图3 PUMA560 简化模型Fig.3 Simplified model of PUMA560

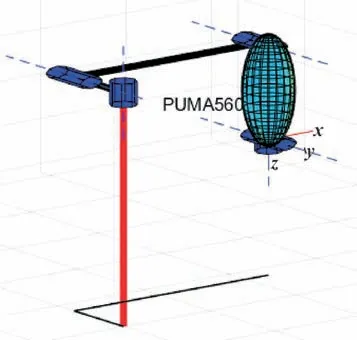
图4 椭球体包围机器人连杆和关节Fig.4 The ellipsoid surrounding the robot connecting rods and joints

椭球体的主轴长决定于连杆长，取连杆的中点为椭球体的中心，则每一个椭球体代表相对应的每一个连杆。根据PUMA560 机器人连杆参数，设置第3 个连杆，即末端连杆的椭球体参数，椭球体中心为机器人运动时实时反馈的连杆中心的位置坐标，椭球体的3 个主轴根据PUMA560 的参数设置为e1＝250 mm，e2＝120 mm，e3＝125 mm。

由于连杆随关节运动而运动，将杆和关节作为整体被椭球体包围，不再区分关节和连杆，使包围盒结构清晰简单，不用单独考虑连杆和关节各自的碰撞情况，使得计算量减少，提高碰撞检测效率。

2 基于椭球坐标系的最短距离计算

2.1 构建椭球坐标系

椭球坐标系是以某个椭球面为参照面，建立特定的局部坐标系，如图5 所示，椭球体A 的中心为点xCA，椭球体B 的中心为点xCB，以椭球体A 为参照面，建立椭球坐标系ε，以点xCA为坐标系原点，以椭球体A 的长轴和短轴分别为坐标系的x和y轴。

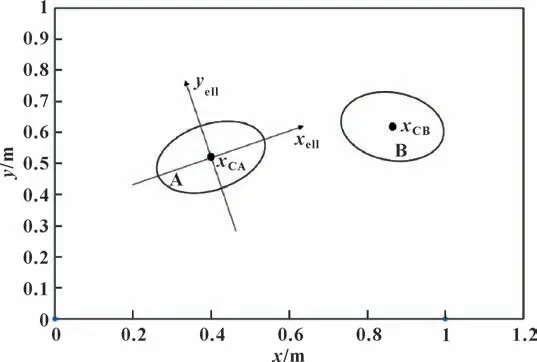
图5 基于椭球体A 建立椭球坐标系εFig.5 Ellipsoidal coordinate system ε based on an ellipsoid A

椭球坐标系中的坐标在笛卡尔坐标系中均满足：

ε＝｛x∈R ｜（x -xCA）TQ（x -xCA）＝1｝，x∈R，Q∈Rm×m，Q＝RDRT，R∈Rm×m，R为三阶单位向量矩阵。

其中：e1、e2、e3为椭球体的3 个半轴长。椭球体A 向量矩阵Q乘以比例因子d的平方转换为矩阵P，d为标量，椭球体坐标系ε中坐标的表达式转化为

其中：P＝d2Q，d表示为椭球坐标系ε中任意的点到坐标系ε原点的距离。椭球坐标系ε在笛卡尔坐标系中的几何意义是同一中心、半轴的单位方向向量相同但长短不同的一系列椭球面，同一椭球面的d值相同，为等高面。椭球体A 在椭球坐标系ε中的d值为1，即为单位椭球。

2.2 等高面求解

椭球坐标系是以等高面来确定两点之间的距离，求解椭球体A 和椭球体B 之间的最短距离问题则转换为求解椭球体B 在椭球坐标系ε中所相切的等高面的问题。

根据等高面（x -xCA）TP（x -xCA）＝d2可知，只需找到位于等高面上任意一点x，则可得到距离的值。由图6 可知，假设椭球体B 和椭球坐标系ε中构建的等高面椭球体A′相切于点xt，即切点xt是属于等高面上的点，求得切点xt的坐标即可求得d的值，但椭球体A 的中心点xCA、椭球体B 的中心点xCB和点xt三点不在一条直线上，而且没有通用的求解两椭球体相切的切点的解析式，只能转换为约束优化问题，目标函数为

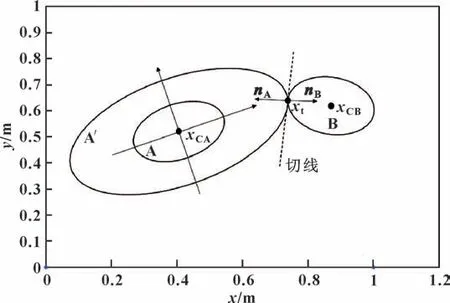
图6 在椭球体坐标系ε 中构建等高面与椭球体B 相切Fig.6 Contour planes constructed in the ellipsoidal coordinate system ε tangent to the ellipsoid B

同时切点xt也在椭球体B 上，所以点xt满足椭球体B 的轨迹方程，则约束条件为

式（2）中：M为椭球体B 的向量矩阵。

由图6 可知，过切点xt指向椭球体A′的法向量nA与过切点xt指向椭球体B 的法向量nB共线但方向相反，则所共线的直线表达式通过对椭球体的向量方程进行求导可得：

其中：t为两个法向量的比例因子。由式（3）可得到xt的表达式：

再将式（4）代入到式（1）中，可得到有关距离d的多项式函数fd（t）：

通过解方程fd（t）＝0 可得到比例因子t的两个根，但因为法向量nA和法向量nB方向相反，因此负根才是满足几何约束的解。将求解得到的负值代入式（4），可得到切点xt的坐标值，再将切点xt的坐标值代入式（5）得到距离d。

2.3 最短欧氏距离求解

基于椭球坐标系求解得到的两椭球体间的最短距离不是笛卡尔坐标系下的欧氏距离，需将椭球坐标系中的相对距离转换为笛卡尔坐标中的欧氏距离。由于每个点的坐标均是笛卡尔坐标系中的坐标值，切点位于椭球体B 上，则通过求解椭球体A 距离椭球体B最近点得到最短欧氏距离。首先求出最短距离所在直线与椭球体A 的交点x0的坐标，然后直接计算切点xt到点x0的欧氏距离。

如图7 所示，先将椭球体A 缩放为单位球A0，沿3 个坐标轴方向对椭球体A 进行缩放，缩放系数分别为1／e1、1／e2、1／e3，得到缩放矩阵T为

图7 等高面缩放变换Fig.7 Contour scaling

缩放变化不改变几何关系，故缩放后的切点坐标xtF仍在最短距离直线上，由于在笛卡尔坐标系中进行坐标计算，椭球体A 的中心点xCA不再为原点，所以缩放后的切点xtF的坐标通过缩放变换求解：

再求点x′t的单位向量x0：

该单位向量的一端端点为单位球A0的中心，因此单位向量x0位于单位球A0上，又因为单位球A0是由椭球体A 进行缩放变换得到的，对单位球A0进行缩放变换的逆变换又可得到椭球体A，故单位向量x0也在椭球体A 上，这时可得到缩放后的最短距离向量dF＝xtF-x0，将最短距离向量dF进行缩放变换的逆变换可得到实际距离向量d＝T-1dF。椭球体A 上距离椭球体B 最短距离的点xA的坐标通过单位向量x0缩放变换的逆变换和椭球体坐标系相对笛卡尔坐标系的平移变换向量xCA的组合变换得到：

最后对实际最短距离向量d求二范数即可得到两椭球体间的最短欧氏距离：

3 多机器人碰撞检测算法

由于机器人的运动轨迹是由机器人末端结构的运动情况决定，因此文中所研究的多机器人碰撞检测算法主要针对机器人末端结构之间的碰撞检测。所要实现的功能是：已知当前时刻多个机器人末端结构的位置坐标，计算出多个机器人末端结构两两之间的最短距离，并与其接触距离进行对比，最终判断多个机器人运动过程是否发生碰撞，如果发生碰撞则确定发生碰撞的运动轨迹范围。

基于椭球体建模的多机器人碰撞检测算法是先根据机器人的结构参数进行建模。作者通过DH 参数法对机器人构建固定连杆坐标系；然后对机器人运动路径进行规划，依据机器人运动学仿真来设定机器人末端连杆的初始位置和目标位置得到规划路径；然后在机器人沿规划路径运动过程中调用最短距离求解函数进行分离距离的求解，最后根据分离距离和接触判断是否发生碰撞。

多机器人碰撞检测算法的流程如图8 所示：首先初始化机器人的DH 参数；通过机器人的DH 参数构建机器人连杆坐标系，获得机器人的简化模型；根据机器人运动学规划机器人运动路径；在已规划的路径上选取合适的时间步长，在轨迹上取样；在轨迹每一个离散时间点上调用基于椭球坐标系最短距离求解算法，获得当前时刻机器人之间的最短距离；输出机器人沿规划路径运动过程中最短距离随时间变化的曲线；最后将最短距离变化曲线与接触距离曲线结合，判断是否发生碰撞。

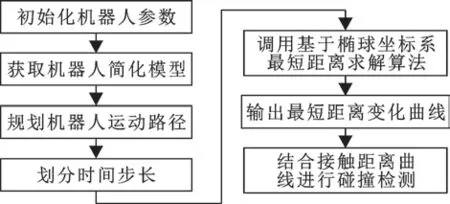
图8 多机器人碰撞检测算法流程Fig.8 Flow of multi-robot collision detection algorithm

针对三机器人进行碰撞检测仿真。三机器人碰撞检测是以双机器人碰撞检测仿真为基础，同时给3 个机器人A、B、C 规划运行轨迹，机器人A 和机器人B 沿相交轨迹运动，机器人B 和机器人C 沿逐渐靠近的轨迹运动，机器人A 和机器人C 沿交叉轨迹运动。可以推测，机器人A 和机器人B 之间的最短距离是是先变小后变大，机器人B 和机器人C 之间的最短距离是逐渐变小，机器人A 和机器人C 之间的最短距离是先变小后变大。在3 个机器人同时运动过程中，对两两机器人之间的最短距离进行求解并判断是否发生碰撞，因此同时输出3 条最短距离变化曲线。

三机器人同时运动的路径规划如图9 所示，3 个机器人A、B、C 分别沿箭头方向同时运动，其中蓝线和黄线在一个平面内且发生相交，红线在蓝线、黄线的平面之外。在3 个机器人同时运动过程中进行碰撞检测仿真，仿真结果如图10 所示，同时输出机器人A 和B、机器人B 和C、机器人A 和C 之间的最短距离变化曲线，均符合推测情况。再和接触距离变化曲线（绿色曲线）相比，判断是否发生碰撞，由仿真结果可知仅机器人A 和B 发生碰撞，符合实际情况。

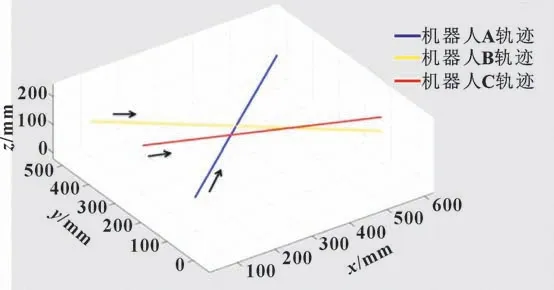
图9 三机器人运动路径规划Fig.9 Three robot motion paths planning

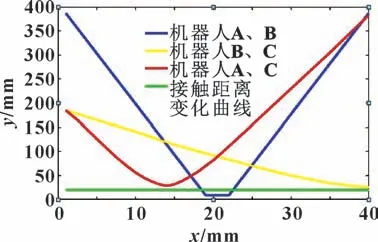
图10 三机器人间最短距离变化曲线与碰撞检测Fig.10 The shortest distance curves between the three machines and collision detection

4 结论

文中针对基于椭球体建模的多机器人碰撞检测方法进行研究，采取离散碰撞检测的方法，在已规划好的路径上划分步长，每一个步长上反复地调用静态最短距离求解算法，从而在每一个步长上进行碰撞检测。文中从反馈物体间的最短距离的角度出发，获取机器人运动时彼此之间的最短距离并由此对多机器人进行碰撞检测。又由于椭球的拉伸性可以较为紧密地包围模型，所以采用椭球体对机器人的连杆和关节进行建模，利用空间几何的相关知识，求解椭球体曲面间的最短距离，从而实现基于距离的多机器人碰撞检测。