影响流量管流量系数的因素分析

马宏伟,屈冬平,张志宏

(1.北京航空航天大学 能源与动力工程学院,北京 100191;2.北京航空航天大学 航空发动机研究院 航空发动机气动热力国家级重点实验室,北京 100191;3.航空工业江西洪都航空工业集团有限责任公司,江西 南昌 330024;4.中国航发四川燃气涡轮研究院 高空模拟技术重点实验室,四川 绵阳 621703)

空气流量是表征航空发动机整机或压气机性能的重要参数之一,准确测量发动机或压气机空气流量对发动机运行、部件匹配至关重要。例如,发动机试验中空气流量测量误差会传递给推力测量,1%的空气流量测量误差可能会造成0.3%的推力测量误差,可以看出,空气流量测量误差会显著影响推力测量精度[1-4]。

目前,国内外普遍采用的流量管均基于流量系数法测量航空发动机整机或压气机部件的空气流量。流量系数法是指测量流量管主流的总温、总压和静压计算流量,再利用校准试验或测量附面层参数获得的流量系数修正该流量。校准试验法是通过校准试验,将流量管测得的流量与标准流量测量装置或较高等级的流量测量装置测得的标准流量相比,得到流量系数。附面层参数法是指将测量的流量管测量截面的附面层参数代入公式计算得到流量系数。美国机械工程师学会(American Society of Mechanical Engineers,ASME)编制的流体流量测量标准中封闭管道中流体流量的测量(Measurement of Fluid Flow in Closed Conduits,MFC)可供参考[5]。

流量系数对流量测量精度有较大影响,由于流量系数是非直接测量获得的,影响测量精度的因素有很多,尤其是在高空模拟试验复杂来流情况下,国标GB/T17611要求流量测量精度不低于0.5%,这给采用流量管测量流量带来了较大的挑战。

劳贤豪等[6]评定了某中小型航空发动机地面试验台进口流量管测量空气流量的不确定度,认为测量误差主要包括流量管喉道直径测量误差,进口气流总温、总压测量误差和流量管喉道处壁面静压测量误差,而流量管附面层修正系数取常数0.995,在此条件下得到了不确定度与空气流量值的关系及大气环境的影响。

张志宏等[7]通过试验和数值模拟研究了某小型航空发动机高空模拟试验台流量管,发现对比校准获取的流量系数只适用于中、低空模拟试验的流量测量,高空模拟试验中流量测量须对流量系数进行修正。

Beale等[8]研究了某地面发动机试验用流量管,发现在高雷诺数下,钟形流量管试验结果和数值模拟结果吻合良好,在低雷诺数(Re=2.0×106)下,二者存在较大差异。数值模拟结果显示:马赫数越大,流量系数越大;雷诺数越大,流量系数也越大;流量系数与测量点位置有关。

史建邦等[9]发现高空条件下流量管附面层位移厚度会随测量截面当地马赫数的增大而增大,空气流量会随测量截面当地马赫数的增大而增大。

向宏辉等[10]研究了某地面压气机试验用流量管,发现马赫数较低时,流量管测量截面静压分布周向差异性较小,随着马赫数的增大,静压周向不均匀度显著增大;附面层厚度会随马赫数的增大而减小,使流量系数随马赫数的增大而增大,这个变化趋势还和流量管尺寸有关。

Herwig等[11]研究发现,粗糙度对层流流动的影响也是不可忽略的。万军伟、黄琨等[12-13]基于试验进一步验证了尼古拉兹发现的圆管沿程损失系数随圆管内流态变化的规律,同时发现尼古拉兹实验略有缺陷,使实验得到的沿程损失系数偏小。李欢等[14]基于尼古拉兹圆管实验,利用颗粒流程序对具有一定粗糙度的圆管进行了模拟,发现圆管壁面粗糙度越大,受扰动的流体范围就越大,当上下游截面的压差一定时,圆管流量随粗糙度的增大而减小。这些研究针对的都是不可压缩的液体工质,关于粗糙度对气体工质流动的影响研究较少,目前基于三维数值模拟方法研究粗糙度对压气机性能的影响有一些相关文献[15-21],其中,考虑粗糙度影响的数值仿真方法值得参考。

事实上,目前流量管测量中存在许多亟须澄清、长期困扰的难题,例如:流量计算公式中的流量系数选取的常数是否能运用到所有工况;不同来流条件下,流量系数是否变化及如何变化;不同流量系数获取方法的差异性和合理性;在流量管使用过程中,壁面磨损或结垢、结冰会导致流量管壁面的粗糙度发生改变,重力等力作用会引起流量管变形或圆度改变,是否会对流量测量产生影响。回答这些问题需要对影响流量管流量系数的因素开展系统的研究。

本文以某航空发动机整机试验装置的流量管为研究对象,对不同条件下流量管内三维流场进行数值模拟,通过布置虚拟测点,建立流量管校准和测量的仿真方法,基于虚拟测量对流量管流量系数获取方法、校准试验测试布局进行研究,分析来流雷诺数、壁面粗糙度和流量管圆度对流量管流量系数的影响,提出改进流量管校准试验、提高流量测量精度的方法。

1 数值模拟试验方法

1.1 流量管几何模型

以某航空发动机整机试验装置的流量管为研究对象,流量管计算几何模型包括前室、导流盆、收敛段和流量管段4部分,如图1所示。整个几何模型为一个回转体,其中,导流盆为双扭线型面,流量管段为试验段,在流量管段插入测量耙进行流量测量。以流量管段进口截面中心为原点,以流向为x轴正方向,基于右手定则建立空间直角坐标系。

图1 流量管计算几何模型

1.1.1 壁面粗糙流量管计算几何模型

采用ANSYS CFX 19.0软件对流量管内的流场进行三维数值模拟。通过在光滑的表面上放置一层紧密排列的等径圆球来模拟粗糙的壁面,ANSYS CFX 19.0对表面粗糙的模拟如图2所示,圆球的直径为hs,即等效沙粒粗糙度,实际物理壁面位于由所有等径圆球球心所确定的平面处,其对流体产生摩阻效应的部分只有圆球hs位置往上的球体。表面粗糙度轮廓如图3所示,y=0处为数值计算时实际物理壁面,y正方向即为粗糙度的测量方向。

图2 ANSYS CFX 19.0对表面粗糙度的模拟

图3 表面粗糙度轮廓

在实际生产制造中,表面粗糙度常用轮廓算术平均偏差Ra来评定,Ra定义为

(1)

如文献[21]所述,等效沙粒粗糙度hs和轮廓算术平均偏差Ra的转换关系为hs=6.2Ra。

根据流量管实际情况,本文研究流量管壁面等效沙粒粗糙度范围为0～160 μm(0代表光滑),间隔为20 μm。

1.1.2 圆度非零计算几何模型

对于流量管段圆度不为零的模拟,简化为流量管段横截面由标准圆变为椭圆,变化过程中周长保持不变,即圆度非零的流量管计算几何模型流量管段横截面为椭圆形。圆度定义为椭圆长半轴长Rmax和短半轴长Rmin之差,即ΔR=Rmax-Rmin,流量管段圆度非零时椭圆横截面如图4所示。

图4 流量管段圆度非零时椭圆横截面

根据流量管实际情况,本文研究流量管圆度变化范围为0 mm、1 mm、3 mm、5 mm、10 mm。

1.2 计算网格和计算方法

采用ANSYS ICEM 19.0软件对流量管计算几何模型手动划分为六面体结构网格,为了提高网格的正交性,主要采用O形网格拓扑结构。对不同网格数量的计算模型进行计算,给定相同的边界条件,采用完全相同的计算方法,监测不同网格数量下流量管内的质量流量,网格无关性验证如图5(a)所示,其中,纵坐标为流量管内质量流量与网格无关质量流量的比值,既为无量纲质量流量。由图5(a)可知,网格数量达到340万个后,质量流量基本不发生变化。基于网格无关性验证结果,确定网格数量为374万个,网格模型如图5(b)所示。本文网格最小正交质量系数为0.8,最大长宽比为1.5,网格质量较优。

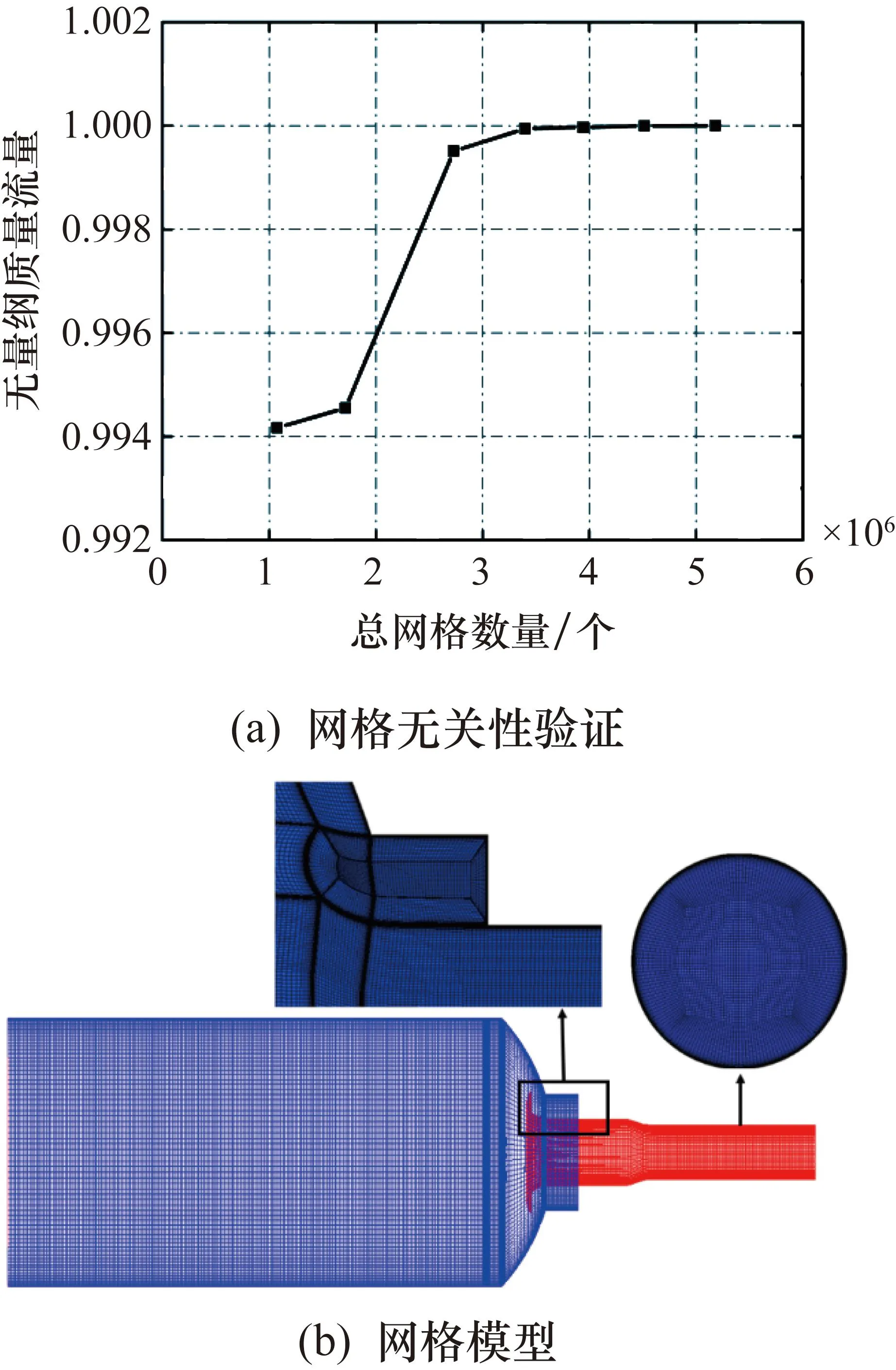
图5 流量管计算网格

本文采用SST(Shear Stress Transport)湍流模型进行计算。边界条件进口给定气流总温、总压及垂直于进口截面的方向,出口给定流量边界条件。本文在研究管内雷诺数(管径为特征长度)、流量管圆度对流量测量的影响时,流量管壁面给定光滑、绝热和无滑移边界条件。本文在研究流量管壁面粗糙度对流量测量的影响时,流量管壁面给定相应的等效沙粒粗糙度,同时给定绝热、无滑移的边界条件。

1.3 仿真方法验证

为了验证本文仿真方法的准确性,对光滑流量管进行仿真计算,基于某一试验工况的测量值(试验数据来自中国燃气涡轮研究院某试验台的试验结果),给定数值计算的进出口边界条件,其中,进口给定总温、总压,出口给定试验测得的流量值,采用上述数值仿真方法,对比这一工况下流量管在同一流向位置处试验测得的总压径向分布和数值模拟得到的总压径向分布,流量管数值模拟结果和试验结果比对如图6所示,其中,横坐标为测点所在位置处的半径(r)和流量管半径(R)的比值,纵坐标为当地总压与进口总压的比值,即为无量纲总压。

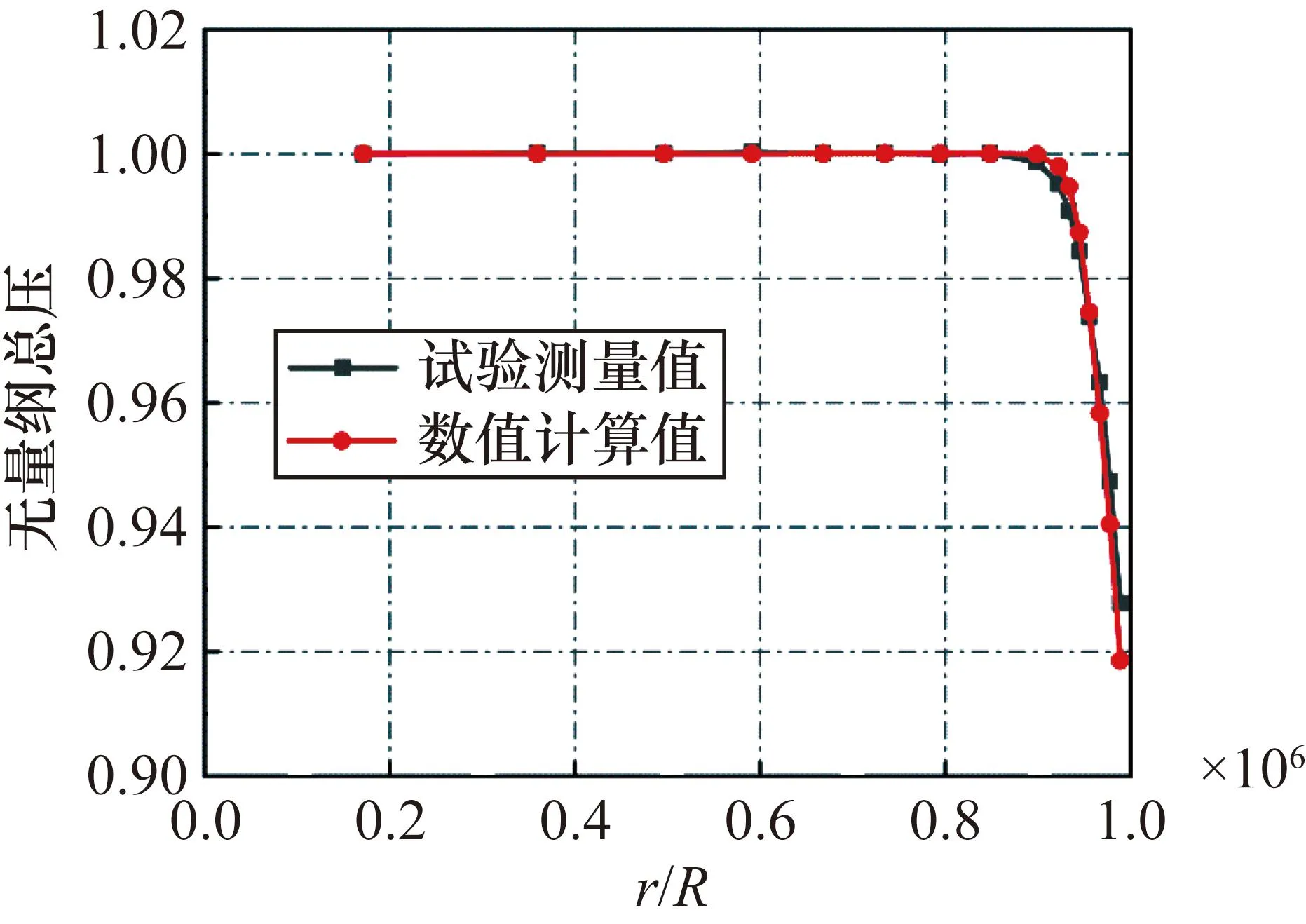
图6 流量管数值模拟结果和试验结果比对

定义数值计算精度Δ为

(2)

式中:Ptsim为数值模拟在测点位置处的总压值,Ptmea为试验中在测点位置处测得的总压值。本次验证算例中,Δ的绝对值小于1%。故试验值与计算值吻合良好,即本文所采用的计算方法能够反映流量管内的流动特性。

基于莫迪图的试验数据,验证本文的数值仿真方法对粗糙壁面流量管的适用性。验证模型为具有表面粗糙度特征的圆管,如图7所示,粗糙圆管的直径D=0.1 m,长度L=10 m。在莫迪图中选取相对粗糙度ε=0.001的曲线和光滑的曲线进行计算,相对粗糙度的计算公式如下:

(3)

图7 粗糙圆管流动计算模型

由式(3)计算可得本次计算的粗糙圆长管等效沙粒粗糙度hs=0.000 1 m。

分别对壁面相对粗糙度ε=0.001和壁面光滑的长圆管流动进行三维数值模拟,其中,粗糙长圆管壁面给定等效沙粒粗糙度hs=0.000 1 m和绝热、无滑移边界条件,光滑长圆管壁面给定光滑、绝热、无滑移边界条件,进气均给定气流总温、总压,气流方向垂直于进口截面的边界条件,出口均给定静压边界条件,均采用SST湍流模型。管道出口马赫数为0.2。在不同雷诺数下分别计算粗糙长圆管和光滑长圆管的沿程损失系数,并与莫迪图中的试验数据进行对比,结果如图8所示。

图8 圆管流动数值模拟和试验值对比

由图8可知,在壁面相对粗糙度ε=0.001及壁面光滑的长圆管内流动的情况下,其不同雷诺数下沿程损失系数的试验值与计算值吻合良好,即本文所采用的计算方法能够反映光滑和粗糙圆管内的流动特性。

1.4 流量管流量系数计算方法

本文基于不同条件下流量管内三维流场的数值模拟,对校准试验法获取的流量管流量系数进行虚拟试验研究,即在流量管测量截面布置虚拟测点进行虚拟测量,由虚拟测点测量气动参数,计算出该截面的测量流量,以仿真模拟计算得到的通过整个流量管截面的理论流量为基准流量或标准流量,基准流量与测量流量的比为流量系数,计算公式如下:

(4)

式中:CB3为校准试验法获取的流量系数;mstd为流量管基准流量;mmea为通过在流量管内虚拟布置静压、总压和总温测点计算得到的测量流量,其计算公式如下

(5)

其中:

(6)

(7)

(8)

同样,本文基于不同条件下流量管内三维流场的数值模拟结果,对附面层参数法获取的流量管流量系数进行虚拟试验研究,即在流量管测量截面布置虚拟测点对附面层参数进行虚拟测量,通过测量附面层位移厚度或附面层厚度,计算得到流量系数。

附面层位移厚度法计算流量系数CB1的计算公式如下:

(9)

式中:δ*为附面层位移厚度,定义如式(10)所示;D为流量管测量段直径。

(10)

式中:ρ、u分别为当地密度和当地速度;ρ0、U0分别为主流密度和主流速度。目前,工程上在进口流量管常用的雷诺数范围内(5.0×105～1.0×107),建立了附面层厚度和附面层位移厚度之间的经验关系式,即两者之比为8[22],可得附面层厚度法计算流量系数CB2的公式如下:

(11)

式中:δ为附面层厚度,为壁面到沿壁面法线上当地流速达到中心主流速度99%处的距离。

2 数值模拟结果分析

2.1 测试布局对流量系数的影响

流量管内测试布局包括两个方面:① 静压、总压和总温测量截面所在的流向位置,用X/D来表征,X为测量截面距流量管段进口的流向距离;② 静压、总压和总温测点的径向位置,用r/R来表征。

本文进行虚拟校准试验时,静压、总压和总温在流量管段同一截面进行测量,静压通过在壁面布置4个静压测点测得,4个静压测点周向均匀分布,总温、总压通过插入4支测量耙进行测量,每支测量耙上布置1个测点同时测量总温、总压,各测量耙上的测点径向位置相同,4支测量耙周向均匀分布,分别与4个静压测点周向位置相同,测点布置方案如图9所示。本次虚拟校准试验研究的测试布局主要考虑测量截面的流向位置及总温、总压测点布置的径向位置。

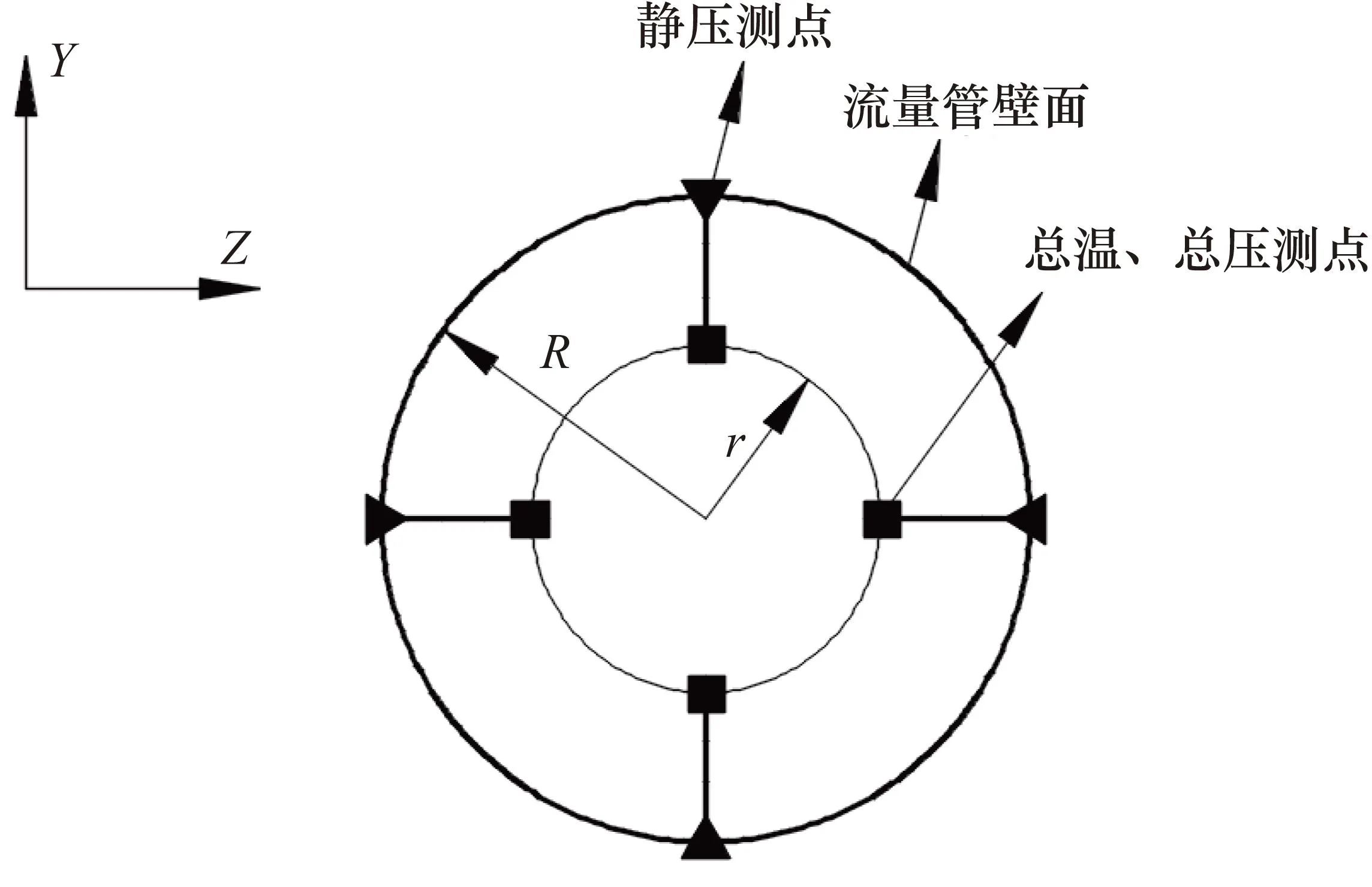
图9 校准试验中测点布置示意图

基于Re=7.9×106、Ma=0.56的工况,首先对比分析校准试验中不同测试布局方案下流量系数的差异。图10对比了总温、总压测点分别布置在r/R为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8和0.9时的径向位置处,测量截面布置在不同流向位置采用校准试验法获得的流量系数CB3。可以看到,测量截面流向位置确定时,总温、总压测点布置在r/R为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8时的径向位置处校准获得的流量系数几乎相同,从X/D=0.5至X/D=2.8,流量系数从0.984沿下游几乎成线性下降到0.97,这是流量管壁面附面层发展造成的。总温、总压测点布置在r/R=0.9径向位置处获得的流量系数相对较大,因为此时总温、总压测点位置接近流量管壁面附面层,其测得的流量值偏小,导致校准获得的流量系数较大。

图10 流量管Re=7.9×106、Ma=0.56工况下不同测试布局的流量系数

图11是测量截面布置在X/D=1.47流向位置,Re=7.9×106、Ma=0.56工况下,总温、总压测点布置在不同径向位置时,虚拟校准试验获得的流量系数分布,可以看到,总温、总压测点布置在r/R<0.8径向位置范围内,流量管流量系数几乎不随总温、总压测点径向位置的变化而变化。在X/D=1.47流向位置,该工况下附面层厚度边界所在位置半径与流量管半径的比值为0.92。

因此,采用校准试验法获得流量系数进行流量测量的流量管,在进行测量布局时,建议在主流区r/R=0.7区附近布置总温、总压测点,没有必要在中心区布置测点,这样可缩短测量耙长度,有效降低堵塞比,减轻测量耙对流场的影响,并可降低测量耙气动负荷,提高测量耙强度和可靠性。

基于Re=7.9×106、Ma=0.56工况的仿真数据,图12对比了测量截面布置在不同流向位置采用附面层位移厚度法、附面层厚度法和校准试验法获取的流量系数,其中,校准试验法测量耙的总温、总压测点径向位置在r/R=0.8处。可以看到,随着测量截面向下游移动,附面层位移厚度法、附面层厚度法和校准试验法获取的流量系数几乎均线性减小,这是由流量管壁面附面层沿流向不断增厚导致的,附面层厚度法获得的流量系数线性下降的幅度稍小。

图12 Re=7.9×106、Ma=0.56工况下不同方法获取的流量系数

由图12可知,测量截面的流向位置在X/D>0.67时,附面层位移厚度法和校准试验法获取的流量系数几乎相同;测量截面的流向位置在X/D为0.9～1.3范围内,附面层位移厚度法和附面层厚度法获得的流量系数差异很小,X/D>2.0后,其差异大于0.002,表明在这些截面采用附面层厚度法获得的流量系数,若用于流量管测量数据处理,将带来0.2%的流量测量误差。因此,即使雷诺数位于5.0×105～1.0×107这一范围内,附面层厚度法的计算公式也不一定适用,其适用性还取决于测量截面的流向位置。建议在Re=7.9×106、Ma=0.56工况下,采用附面层厚度法获取流量管流量系数时,将测量截面的流向位置控制在X/D为0.9～1.3的范围内。

2.2 雷诺数对流量系数的影响

首先对比低雷诺数工况下采取不同方法获取的流量系数的差异。图13为Re=2.2×105、Ma=0.56工况(低雷诺数工况)下,测量截面布置在不同流向位置,分别采用附面层位移厚度法、附面层厚度法和校准试验法获取的流量系数的对比,校准试验中的测点布置方案如图9所示,测量耙上总温、总压测点所在径向位置r/R=0.8。可以看到,对于Re=2.2×105、Ma=0.56工况,测量截面布置在X/D>0.67的流向位置,采用附面层位移厚度法和校准试验法获取的流量系数相同,但显著小于采用附面层厚度法获取的流量系数。

与图12所示的Re=7.9×106、Ma=0.56工况(高雷诺数工况)下的结果相比,Re=2.2×105、Ma=0.56工况下用附面层位移厚度法和附面层厚度法计算得到的流量系数差值较大。在Re=7.9×106、Ma=0.56工况下,随着测量截面沿流向移动,附面层位移厚度法和附面层厚度法计算的流量系数的差值的绝对值先减小后增大,在X/D=1.1处两种方法计算的流量系数相等,测量截面布置在同一流向位置,采用附面层位移厚度法和附面层厚度法计算流量系数的差值的绝对值不大于0.005;在Re=2.2×105、Ma=0.56工况下,随着测量截面移向下游,附面层位移厚度法和附面层厚度法获得的流量系数的差值逐渐增大,在X/D=2.8的位置,差值达0.027。

为了研究采用附面层厚度法计算流量系数的适用性,对比不同雷诺数下附面层厚度和附面层位移厚度之比δ/δ*沿流向的变化如图14所示。在同一流向位置,雷诺数越小,δ/δ*越小;在X/D>1.1的流向位置范围,在同一流向位置,随着雷诺数降低,δ/δ*逐渐偏离8,即随着雷诺数降低,附面层位移厚度法和附面层厚度法计算的流量系数的差值的绝对值增大。公式δ/δ*=8工程上约定适用的雷诺数范围为5.0×105～1.0×107,本文研究结果显示,即使雷诺数位于这一范围内,公式δ/δ*=8也很难成立,例如Re为1.1×106、2.0×106、4.0×106、5.7×106、7.9×106的工况下,在X/D>1.1的流向位置,δ/δ*<8,甚至对于Re=1.1×106、Ma=0.56的工况,在X/D>1.1的流向位置,δ/δ*<7。由此可知,附面层厚度法得到的流量系数不够准确,尤其是在低雷诺数工况下,应采用附面层位移厚度法或校准试验法获取流量系数。

图14 不同雷诺数下的δ/δ*

图15为测量截面布置在不同的流向位置,不同雷诺数下采用附面层位移厚度法获得的流量系数对比,由图15可知,随着测量截面移向下游,流量系数不断减小。这是因为各工况下流量管内的流动均未进入完全发展段,附面层沿流向不断增厚。随着管内雷诺数降低,流量管段附面层增厚,故在同一流向位置,流量系数随管内雷诺数的降低而显著减小。

图15 不同雷诺数下附面层位移厚度法获得的流量系数

以测量截面布置在X/D=1.47流向位置为例,Re=7.9×106、Ma=0.56工况下的流量系数比Re=2.2×105、Ma=0.56工况下的流量系数大0.018,也就是说,两种工况下的试验测量若采用其中一个工况下的流量系数进行数据处理,那么另一个工况获得的流量结果会有1.8%的测量误差。

进一步推论,在地面高雷诺数工况下校准得到的流量系数不适用于高空低雷诺数工况下的流量测量。为了保证流量管在不同雷诺数工况下的测量精度,需要对不同雷诺数下的流量管进行校准,用相同雷诺数下的流量系数对流量管的实际测量数据进行处理。

2.3 粗糙度对流量系数的影响

图16(a)和图16(b)分别为Re=7.9×106、Ma=0.56工况和Re=2.2×105、Ma=0.56工况下,不同等效沙粒粗糙度下,附面层厚度和附面层位移厚度比值δ/δ*随测量截面流向位置的变化,图17(a)和图17(b)分别为Re=7.9×106、Ma=0.56工况和Re=2.2×105、Ma=0.56工况下,不同等级粗糙度下,采用附面层位移厚度法计算的流量系数随测量截面流向位置的变化。

图16 不同等效粗糙度下的δ/δ*

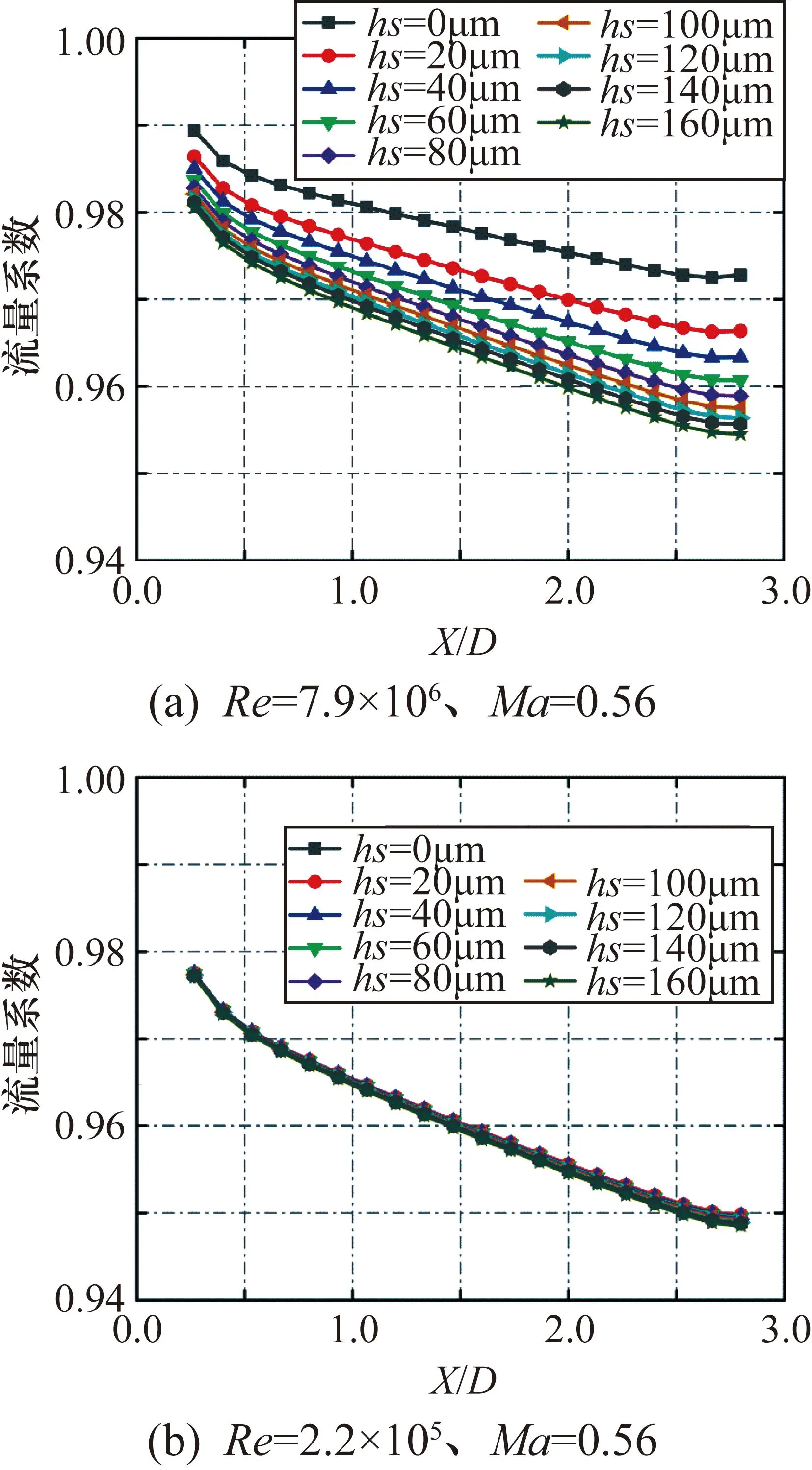
图17 不同等效粗糙度下附面层位移厚度法计算的流量系数

由图16可知,测量截面的δ/δ*随X/D的增大而逐渐减小。在Re=7.9×106、Ma=0.56工况下,在同一流向位置,δ/δ*随着粗糙度的增大而减小,在X/D>1.1的流向位置范围内,同一流向位置,随着粗糙度增大,δ/δ*逐渐偏离8,甚至可达6,这表明高雷诺数工况下,流量管壁面粗糙度较大时,δ/δ*偏离8较严重,不可采用经验的附面层厚度法获得流量系数,否则会带来较大的流量测量误差。图17表明,附面层位移厚度法获得的流量系数随粗糙度的增大而减小。

相较于Re=7.9×106、Ma=0.56工况,Re=2.2×105、Ma=0.56工况下,δ/δ*和采用附面层位移厚度法得到的流量系数均对粗糙度的变化较不敏感,这主要是由于低雷诺数工况下,受雷诺数的影响,流量管壁面附面层较厚,壁面粗糙处流体流速较低,粗糙度几乎不影响附面层的发展。以X/D=1.47的流向位置为例,当粗糙度由0增大到160 μm时,Re=7.9×106、Ma=0.56工况下的δ/δ*减小1.49,而Re=2.2×105、Ma=0.56工况下的δ/δ*减小0.02;Re=7.9×106、Ma=0.56工况下的流量系数减小0.027,而Re=2.2×105、Ma=0.56工况下的流量系数减小0.001,几乎可以忽略粗糙度对流量管低雷诺数工况下流量测量的影响。

可得出结论:对于高雷诺数工况,在流量管壁面光滑时获取的流量系数不适用于管壁粗糙时的流量测量的数据处理,否则会带来较大的流量测量误差。实际试验测量前,要密切关注流量管内壁粗糙度的变化,及时清洁或校准流量管,当流量管壁面较粗糙时,建议采用附面层位移厚度法或校准试验法获取流量系数,以消除流量管壁面粗糙度对高雷诺数工况下流量测量的影响。

2.4 圆度对流量系数的影响

本文在研究圆度对流量测量的影响时,流量管圆度不为零简化为流量管段横截面由标准圆变为椭圆,周长保持不变。进行虚拟测量时,4个静压测点分别布置在椭圆的上顶点、下顶点、左顶点、右顶点上,4支测量耙分别位于椭圆的两个长半轴和两个短半轴上。图9给出了流量管横截面为标准圆时,各测量方案测点所在的位置,其表征方式是测点处的半径与流量管段的半径的比值。流量管段圆度不为零、横截面为椭圆时,位于长半轴上的测点的所在位置的表征方式为以椭圆中心为原点,测点处的半径与椭圆长半轴的比值;位于短半轴上的测点,其所在位置的表征方式为以椭圆中心为原点,测点处的半径与椭圆短半轴的比值,各测量方案测点相对位置的数值同前。流量管圆度改变,其测量截面面积会发生改变,而在实际测量中,会忽略圆度引起的测量截面面积的变化,基于数值模拟对试验过程进行仿真,本文在流量管内布置虚拟测点测量数据计算空气流量时,仍代入流量管圆度为零时测量截面的面积进行计算。

图18(a)和图18(b)显示了Re=7.9×106、Ma=0.56工况和Re=2.2×105、Ma=0.56工况下,随着X/D的增大,不同圆度下附面层厚度和附面层位移厚度比值δ/δ*逐渐降低;相同圆度下,高雷诺数下的δ/δ*值明显高于低雷诺数下的值;高雷诺数下的δ/δ*值随圆度的增大略微减小,低雷诺数下的δ/δ*值随圆度的增大略微增大,以测量截面布置在X/D=1.47的流向位置为例,当流量管圆度在0～10 mm范围变化时,δ/δ*变化都不超过0.5,这是由流量管附面层的分布特性决定的。

图18 不同圆度下的δ/δ*

图19(a)和图19(b)显示了Re=7.9×106、Ma=0.56工况和Re=2.2×105、Ma=0.56工况下,不同圆度下附面层位移厚度法计算的流量系数随X/D的增大逐渐减小,低雷诺数工况下减小幅度较大,主要是由相应的雷诺数下流量管附面层的发展特性决定的。由图19可知,无论是在高雷诺数还是低雷诺数工况下,附面层位移厚度法获得的流量系数对流量管圆度的变化均不敏感。以Re=7.9×106、Ma=0.56工况为例,当测量截面布置在X/D=1.47的流向位置时,采用附面层位移厚度法获得的流量系数随圆度的增大而略微减小,流量管圆度在0～10 mm范围变化,变化不超过0.001,这主要是由于该范围内圆度变化对附面层测量的影响较小。

实际工程中,流量管圆度的变化不仅是朝椭圆形变化,同时圆度的变化直接影响流量管测量截面的面积,对流量管测量截面附面层分布的影响很难用有限的附面层测点充分体现出来,因而对有变形的流量管,附面层位移厚度法较难准确获得流量管的流量系数,建议采用校准试验方法获得有变形的流量管的流量系数。

3 结论

① 附面层位移厚度法和校准试验法获取的流量系数接近,附面层位移厚度法和附面层厚度法在同一测量截面获得的流量系数并不总是相等,和测量截面的流向位置有关。

② 在同一流向测量截面,流量系数随流量管内雷诺数的减小而减小,随流量管壁面粗糙度的增大而减小;低雷诺数工况下,流量系数对粗糙度变化不敏感。

③ 当处于低雷诺数工况或者流量管壁面粗糙度较大时,应采用附面层位移厚度法或校准试验法获取流量系数,不建议采用附面层厚度法获取流量系数。

④ 流量系数对流量管圆度的变化不敏感,建议采用校准试验方法获得有变形的流量管的流量系数。

⑤ 尽量采用附面层位移厚度法或校准试验法获取流量管宽雷诺数范围的流量系数。应采用流量管实际测量工况下的雷诺数对应的流量系数,修正流量管测量数据,才可保证流量测量精度。