垂直应变对Graphene/GaN异质结肖特基势垒和光学性质的影响
秦云辉,陈兰丽,余宏生
(湖北理工学院 数理学院,湖北 黄石 435003)
石墨烯是一种典型的二维材料,因存在零带隙而限制了在实际生活中的应用。大多数单层二维材料都具有半导体特性,而且具有可裁剪的带隙宽度。因此,其他二维材料(如单层MoS2、单层ZnO、单层GaN)[1-2]陆续应用于各种场效应管、光探测器中,石墨烯状单层GaN尤其引起了学者的广泛关注。Durgun等[3-4]采用理论计算证实单层GaN是稳定的,从头分子动力学计算角度证明单层GaN在高温时是稳定的,并发现单层GaN是间接带隙半导体。2016年,通过迁移增强型封装生长(MEEG)技术和石墨烯外延生长,Balushi等[5]成功合成了二维单层GaN材料,并且认为该材料是纳米电子学和光电子学优选材料之一。Du等[6]发现通过化学功能化单层GaN,可以有效调控其带隙,使其满足电子器件和光电器件的需求。
近些年,以单层石墨烯结构形成的异质结已经得到了广泛研究。马浩浩等[7]发现非金属原子掺杂WSe2可以有效调控WSe2/graphene异质结肖特基势垒的类型和高低,当C和O原子掺杂WSe2时,肖特基类型由p型向n型转变。张芳等[8]发现graphene/InSe范德瓦尔斯异质结在界面处形成欧姆接触。在外电场作用下,其肖特基势垒高度和接触类型都可以有效调控。Liu等[9]采用第一性原理计算方法发现垂直应变可以调控graphene/AlN异质结的肖特势垒高度。目前,通过改变层间距调控graphene/GaN异质结电子性质的研究比较少。因此,本文选取石墨烯和GaN晶格匹配较好的超胞搭建异质结模型,采用密度泛函理论,通过改变层间距调控graphene/GaN异质结的肖特基势垒和光学性能,旨在为研究范德瓦尔斯效应场效应管和晶体管提供了一定的理论依据。
1 计算方法
所有计算都基于密度泛函理论结合PAW方法,在Vienna从头计算软件包(VASP)下实现。其中,互关联势是采用Perdew-Burke-Ernzerhof (PBE)方法,基于广义梯度近似(GGA)[10-11]。体系中Ga、N、C原子的价态电子组态分别为:4s24p1、2s22p3、2s22p2。平面波截断能设置为550 eV,布里渊区k-points采样选取7×7×1。在结构弛豫时,离子步力收敛最大达到1 meV/Å,电子步能量达到最小1.0×10-5eV。在计算模型中,为了避免层间相互作用,异质结沿着z方向上设置真空层厚度为15 Å。层间的范德瓦尔斯效应,即van der Waals (vdW),都采用D2-Grimme (DFT-D2)修正,以更好地描述长程vdW相互作用。
2 结果与讨论
在构建graphene/GaN异质结模型之前,石墨烯和单层GaN必须先弛豫。单层石墨烯和单层GaN几何结构和能带结构如图1所示。计算得到石墨烯的晶格常数为a=b=2.459 Å;而单层GaN的晶格常数为a=b=3.216 Å。如图1(c)所示,单层石墨烯的带隙为0 eV,表明Dirac点位于高对称K点位置,具有半金属特征。然而,单层GaN的价带顶位于Γ与M点之间,且其导带底在Γ点。因此,单层GaN为间接带隙半导体,其带隙大约为2.0 eV,与以前的基于自旋极化计算的能带带隙为2.12 eV[6]相一致。
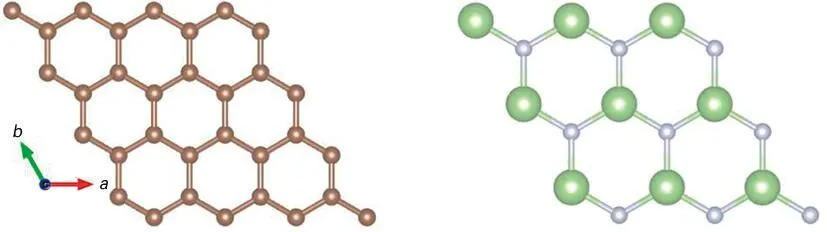
(a) 单层石墨烯几何结构 (b) 单层GaN几何结构
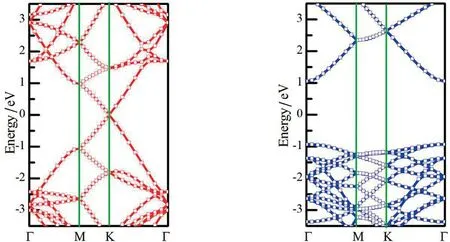
(c) 单层石墨烯能带结构 (d) 单层GaN能带结构
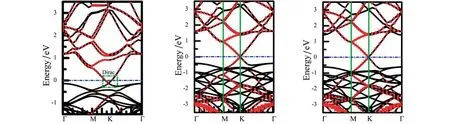
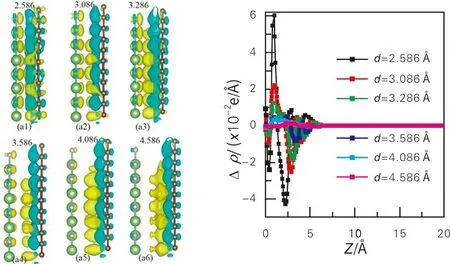
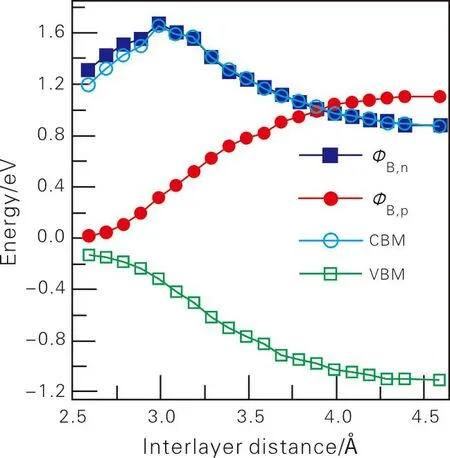
graphene/GaN异质结结构如图2所示。该结构是由4×4石墨烯超胞和3×3单层GaN超胞构建而成。为了寻找最稳定的异质结,改变graphene和单层GaN之间的距离d(2.5 Å (a) 顶视图 (b) 侧视图 Eb=(Egraphene/GaN-Egraphene-EGaN)/N (1) 式(1)中,Eb为束缚能;Egraphene/GaN为异质结总能;Egraphene为单层石墨烯的总能;EGaN为单层GaN的总能;N为碳原子的数量。 束缚能随层间距变化的曲线如图3所示。从图3得知,最小束缚能所对应的结构为最稳定结构,所以,最稳定graphene/GaN结构所对应的层间距为3.286 Å,这一结果与Sun等[12]基于HSE06计算得到的最稳定结构所对应的3.28 Å相一致。 图3 束缚能随层间距变化的曲线 不同层间距下graphene/GaN异质结的能带结构如图4所示。 (a) d=2.586 Å (b) d=3.086 Å (c) d=3.256 Å (d) d=3.586 Å (e) d=4.086 Å (f) d=4.586 Å 从图4可以看到,graphene/GaN异质结的能带结构主要由graphene的能带结构和GaN的能带结构两部分叠加,形成的异质结保留了各自电子结构的特征。很明显,价带顶和导带底的位置相对于费米能级出现了一定的偏移。当2.5 Å≤d≤4.586 Å时,graphene/GaN异质结整体的能带结构没有发生变化,说明没有成键的C-p态电子在大于π键内以费米速度运动。此时,graphene的导电类型没有受到GaN影响。然而,graphene的价带顶和导带底发生相对的偏移,也就是说n型肖特基势垒和p型肖特基势垒高度发生了一定的改变。当d=2.586 Å时,graphene/GaN异质结中肖特基接触类型演变为p型。当层间距从2.586 Å增加到4.586 Å时,graphene/GaN异质结导带底发生变化,逐渐向费米能级位置移动,graphene/GaN异质结中肖特基接触类型由p型转变为n型。而另一方面,价带顶逐渐减小,远离费米能级,异质结的肖特基势垒逐渐转变为n型,但是肖特基势垒的大小变化很小。在这过程中,费米能级相对于2.586 Å时明显上移,使得石墨烯Dirac点偏移费米能级。从图4(a)中可以明显看到Dirac点,费米能级位于其上方,graphene/GaN异质结接触类型表现出p型接触。综上所述,改变异质结层间距,可以调控graphene/GaN异质结的接触类型和肖特基势垒高度。 考虑到graphene/GaN异质结中graphene和GaN层之间的相互作用导致异质结间电荷转移和分布发生重排,从而使graphene/GaN异质结的肖特基接触类型发生改变。因此,分析各不同层间距下graphene/GaN异质结的差分电荷密度和平面电荷密度。差分电荷密度和沿着z方向的平面差分电荷密度如图5所示。 (a) 差分电荷密度 (b) 沿着z方向的平面差分电荷密度 图5(a)中a1~a6中等值面的值分别为1×10-3、5×10-4、2×10-4、2×10-4、5×10-5、2×10-5e/Å3。整体来看,电荷消耗区域在石墨烯层附近,表明石墨烯失去电子,变成富空穴层;而电荷积累区域在GaN附近,为富电子层。当层间距为2.586 Å时,界面靠近GaN一侧聚集的正电荷最多,同时graphene层负电荷较多,此时graphene/GaN异质结的接触类型为p型,而且费米能级的位置较低。由图5(b)得知,当石墨烯与GaN形成异质结时,电荷从石墨烯转移到GaN层,从而在界面处形成一个由GaN指向石墨烯的内建电场。当光照射在graphene/GaN异质结时,电子从GaN层的价带跃迁到导带,在上述的内建电场作用下,电子从GaN层的导带跃迁到graphene层。从某种程度上,内建电场有利于分离光生电荷。随着层间距增加,界面电荷聚集很少,费米能级的位置发生一定偏移,异质结的肖特基接触类型发生转变。当层间距逐渐增加到4.086 Å时,界面基本没有电荷转移,但是异质结的接触类型表现为n型。由此可以得知,层间距增加导致界面电荷转移量由多变少,使费米能级的位置发生一定偏移,从而调控肖特基接触类型,使得其由p型接触向n型接触转变。当层间距达到4.586 Å时,界面的电荷转移基本为0,异质结保持为n型,其势垒大小变化不大。这主要是较大的层间距阻挡电荷转移,使费米能级在导带下方产生“钉扎”现象。 不同层间距下graphene/GaN异质结的静电势如图6所示。 图6 不同层间距下graphene/GaN异质结的静电势 随着层间距减小,更多电荷从石墨烯转移到单层GaN。在层间距减小过程中,异质结中石墨烯能级降低,接近异质结中GaN的价带,导致其价带接近费米能级,最后形成p型肖特基接触。 为进一步讨论不同层间距下graphene/GaN异质结的肖特基势垒高度和肖特基类型,计算了graphene/GaN异质结中单层GaN部分的导带底、价带顶以及肖特基势垒高度随着层间距的变化关系,如图7所示。由图7可知,当d<3.586 Å时,肖特基势垒类型表现为p型;反之,表现为n型。当层间距为2.586、3.086、3.286、3.586 Å时,异质结的p型肖特基势垒为0.015、0.413、0.620、0.819 eV;当层间距为3.986、4.086、4.586 Å时,界面的肖特基势垒分别为0.975、0.948、0.881 eV,其肖特基势垒类型由p型转变为n型。由于出现费米能级“钉扎”效应,后期肖特基势垒高度基本不变。 图7 graphene/GaN异质结中单层GaN部分的导带底、价带顶以及肖特基势垒高度随着层间距的变化关系 graphene/GaN异质结、单层graphene、单层GaN的光吸收系数如图8所示。从图8中可以看出,和单层石墨烯、单层GaN相比,异质结的形成导致可见光区域和紫外光区域的光吸收强度增加。沿着x轴方向,光能量分布主要分3段:0~5.40 eV主要由graphene贡献;5.40~10.67 eV主要由GaN层贡献;10.67~30 eV主要由graphene贡献。沿着z轴情况却不同:0~11.43 eV主要由GaN贡献;而11.43~30 eV主要是由graphene提供。同样的结论也在其他异质结中进行了预测。 (a) 沿着x轴方向 (b) 沿着z轴方向 综上所述,层间距不仅可以有效控制graphene/GaN异质结的肖特基势垒及类型,而且还可以提升其在可见光和紫外光区域的光吸收,有助于改善可控纳米电子及光电子器件的性能。 通过密度泛函第一性原理计算方法研究了graphene/GaN异质结的界面特性、肖特基接触以及光学性能,结果表明异质结中graphene和GaN中存在微弱的范德瓦尔斯作用。在形成异质结后,graphene和GaN保持各自的电子特性。随着层间距增加,graphene/GaN异质结肖特基类型由p型向n型转变。graphene与GaN层间电荷转移和费米能级位置偏移是肖特基势垒高度以及肖特基类型发生转变的主要原因。另一方面,graphene层电荷减少,GaN层电荷增多,从而导致电荷从graphene层向GaN层转移,导致了内建电场的形成,进而分离光生电荷。这些结果可为设计与制备场效应管提供可靠的理论支持。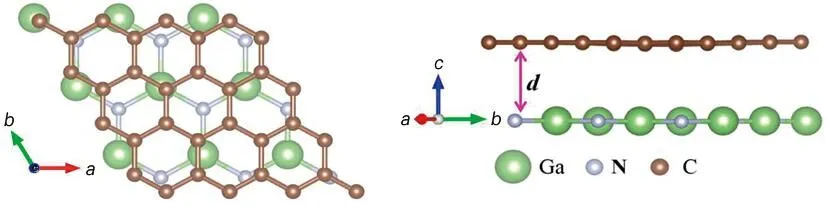





3 结论

