基于FAHP的高职院校教师信息化教学能力综合评价

刘 涛,孙 倩,陈 昕,徐敬广

(安徽电子信息职业技术学院 电子工程学院,安徽 蚌埠 233060)

当前,信息技术迅猛发展,已经在高等职业教育领域产生了深远的影响。提升高职教师的信息化教学能力,突破点在于引导教师在信息技术支撑的全新学习环境下实现教学方法与模式的创新[1]。《教育信息化2.0行动计划》《教育信息化“十四五”规划》都重点强调了“信息技术与教育教学深度融合”,要求教师要应用信息技术提升教学水平、创新教学模式[2-4],对教师信息化教学能力的要求将越来越高。

随着国家“双碳”战略的提出和“三教”改革的深入,作为高职教学活动的主导者和实施者,高职教师也要积极应对和主动适应高等职业教育改革的新趋势,不断提升自身及教学团队的信息化教学能力,增强适应性,把好人才质量第一关。

1 构建基于FAHP算法的高职教师信息化教学能力综合评价模型

1.1 研究方法

结合高职教师的教学工作特点以及信息化教学现状,韩锡斌等[1]设计了基于模糊数学的信息化教学能力综合评价表,组建了评价小组,并按照信息化教学能力综合评价表进行评分,划分等级,提出改进建议。参考教育部教师工作司“中国高校教师专业发展调研”项目的研究成果,信息化教学能力综合评价表从信息技术融入教学的意识、素养、能力和研究等4个维度构建高职教师信息化教学能力综合评价体系[1,5]。

通过问卷星收集专家组的评分情况,融合模糊数学的逐项分配法,进而可以得到信息化教学能力的综合评价结果。根据打分范围,将高职教师的信息化能力分为A、B、C、D、E五个等级;整改建议主要针对D和E等级的教师,列出信息化教学能力的不足方面,并提供相应的改进建议。

1.2 FAHP分析模型

高职院校教师的信息化教学能力综合评价本质上是一个模糊概念,涉及很多的因素,比较适合采用FAHP(模糊层次分析)算法。该方法将分析对象进行分解,并将其中所包含的评价元素即探索性因子[1]分解为两个层次,定量分析各探索性因子和评价数据,确定各探索性因子的权重,确定权重向量：α=(α1,α2,…,αm)。依据文献[1]确定评价集：u={u1,u2,…,un},其中n为影响综合评价信息化教学能力评价的探索性因子个数。

借助问卷星平台统计出来的专家组成员独立评分情况,确定第1层和第2层对应的指标得分。将权重进行归一化处理后,再与专家评分相结合,求得第1层探索性因子的模糊关系矩阵R。评价向量由u和V组成,进而形成了评价模糊矩阵Ri：

(1)

式(1)中,m表示第n个指标中第m项的探索性因子。

将权重向量与第2层探索因子的模糊关系矩阵相结合,可求得对应探索性因子的综合得分向量ui：

(2)

式(2)中,b为赋予权重后的得分向量。

对第2层探索性因子的得分向量依次排序,得出第1层探索性因子的关系矩阵。

(3)

将第2层探索性因子的得分向量与第1层探索性因子权重的得分矩阵相结合,进行模糊综合评价。

(4)

依据划分的评价集各层的边界,以及评价集对应的分割阈值向量α=(α1,α2,…,αt),得到最终的综合评价得分：

g=(b1,b2,…,bt)·(α1,α2,…,αt)T

(5)

在多级模糊综合评价中,为了保证评价的完整性,为教师本人与教学管理人员提供更精准的评价分析,进一步分别计算第1层探索性因子和第2层探索性因子各项得分。

gi=(u1,u2,…,ut)·(α1,α2,…,αt)T

(6)

gij=(ui1,ui2,…,uit)·(α1,α2,…,αt)T

(7)

2 实证研究

组建15人的评价小组,评价小组成员包括信息化教学比赛评委、获奖选手、教学督导及管理人员、一线教师及在读学生,利用问卷星进行评分数据采集。根据各自经验对本校某位教师的各探索性因子进行评分,确定各因子的权重。先将影响因素分解为两个层次的探索性因子,然后将第2层因子与第1层因子进行比较,构造判断矩阵。通过计算判断矩阵,对层次进行单排序和层次分级,对数据做归一化处理与分析,得到相应的指标权重和模糊关系矩阵[6],进而得到高职院校教师信息化教学能力综合评价分析结果。

2.1 计算及结果分析

根据问卷星收集的评价小组打分,得到第1层探索性因子和15个第2层探索性因子的值(见表1);从而可以得出第1层探索性因子的模糊关系矩阵。

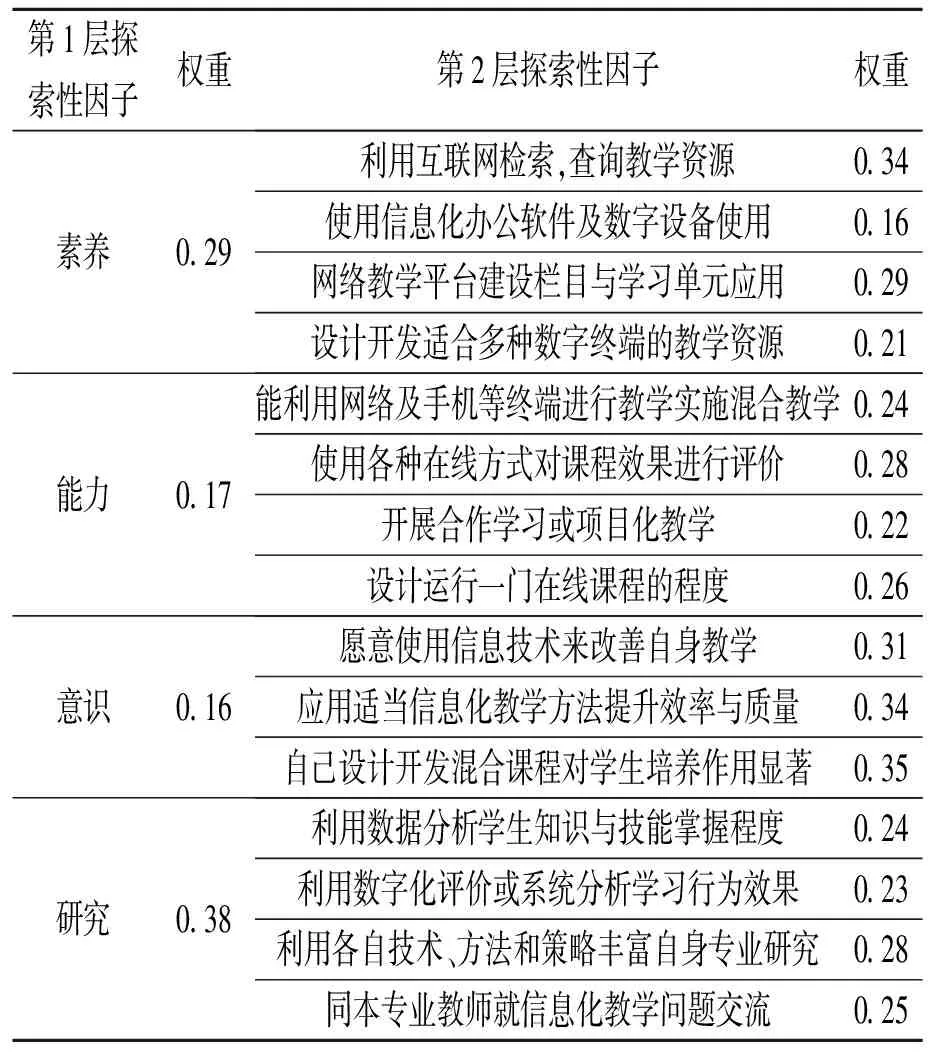
表1 探索性因子权重

单因子评价矩阵R可根据各探索性因子集中程度求得。先逐个进行单因子评价,例如对于利用互联网检索,查询教学资源探索性因子,55%的组员认为A,15%的组员认为B,22%的组员认为C,8%的组员认为D,则得到评价集为{0.55,0.15,0.22,0.08,0};同理,可以得到其他评价集的数据;而后将所有单因子评价结合起来从而得到判断矩阵,即：

利用公式(4)可以得到第1层探索性因子的综合得分向量：

根据上述第1层探索性因子得分向量,利用公式(5),将临界值向量α=(4,3,2,1,0)分别对应于确定信息化教学能力,即：{很强,强,一般,较弱,弱}即A、B、C、D、E五个等级;进而可以得到教师信息化教学能力综合评价得分。教师信息化教学能力综合评价得分：g=(0.506,0.3273,0.1413,0.0265,0)·(4,3,2,1,0)T=3.32。

利用公式(6)可计算出第1层探索性因子得分,分别为3.24、3.48、3.12、3.39。再利用公式(7)可计算出相应的探索性因子得分。利用FAHP模型计算得分情况见表2。

表2 利用FAHP模型计算得分情况

2.2 一致性检测

在对多个元素进行比较时,人为判断难以保持完全一致。为了使对探索性因子重要性的比较保持逻辑一致性,必须进行一致性检验。若一致性比率小于0.1,则表明检验合格[7];否则,判断矩阵需要重新构造[8]。

(8)

式(8)中,CR为随机一致性比率;Ri为平均随机一致性指标。当CR<0.1时,表明判断矩阵满足要求。

对于1至5阶的判断矩阵平均随机一致性指标Ri取值情况,见表3。通过计算本模型评价的CR<0.01,表明权重分配较为合理。

表3 Ri取值情况

3 结语

参考教育部教师工作司“中国高校教师专业发展调研”项目研究成果,从信息技术融入高职教育教学的意识、素养、能力和研究等4个维度构建高职教师信息化教学能力综合评价框架,利用FAHP算法构造高职教师信息化教学能力综合评价模型,以某位教师的实际得分情况进行了模型计算,从而得出相对客观的综合评价结果,为高职院校教师信息化能力评价提供一定的参考和借鉴。