基于可变形卷积的轴承剩余寿命预测

周立俭,卜振飞,耿增荣,孙伊萍,周玉国

(青岛理工大学 信息与控制工程学院,青岛 266525)

轴承是机械设备运转过程最容易损坏的部件,例如在交流同步、交流异步、直流电机中轴承的损坏比例分别为51%,41%和42%[1]。为了避免轴承损坏造成安全生产事故,建立了基于数据驱动的健康评估框架、工业装备故障预测与健康管理(简称PHM)系统[2]。轴承作为PHM中的核心,对其进行剩余寿命(RUL)预测可以避免机械设备突发事故造成的损失,具有重要的现实意义。

随着深度学习技术的发展,相关理论的完善,基于数据驱动的预测方法中,利用深度学习进行RUL预测逐渐成为主流。马占伟等[3]建立了多尺度卷积神经网络(CNN)对轴承数据进行特征提取,构建退化指标;张继冬等[4]则是建立了基于全卷积的预测网络,去掉神经网络中的全连接层来减少神经网络需要训练的参数。为了利用轴承数据之间的时序相关性,蔡薇薇等[5]先对轴承数据进行频域特征提取,然后利用卷积神经网络(CNN)与长短期记忆网络(LSTM)组成的预测模型进行深层特征提取和RUL预测。孙世岩等[6]利用动态时间规整算法扩增数据集训练预测网络BLSTM;而为了使网络在特征提取时得到更为有效的退化特征,DU等[7]将全局注意力结构加入预测网络用以调整退化特征的贡献度。

上述基于深度学习网络建立的预测模型,不管是利用CNN还是LSTM进行特性提取时,数据稍微平移,绝大多数CNN的输出会发生变化,而可变形卷积[8]在每个卷积采样点上增加了偏移量,可以获得不规则数据的不变特征。但因为可变形卷积的参数计算量较大,太多可变形卷积的堆叠会造成计算负担太大,因此本文在使用较少可变卷积核的基础上进一步利用注意力机制、普通的卷积计算和残差结构构建了基于可变形卷积的RUL预测模型(ADRN),减小计算负担的同时也提高了预测精度。又因为预测网络越来越复杂,如果不对网络训练加以约束,网络权重更新就变得不稳定,为使网络在面对异常数据时也能有效调节网络训练的权重,本文在训练过程中提出了基于均方误差(MSE)与均方根对数误差(RMSLE)的动态损失函数。

因为原始的轴承数据变化是非平稳的,很难体现出轴承的退化趋势,ZHU等[9]在轴承的RUL预测工作中,采用小波变换获得轴承原始数据的时频特征图作为模型输入,与使用原始信号或时域、频域特征相比,在CNN预测网络中取得了更好的RUL预测精度。因此本文首先使用了连续小波变换(CWT)提取轴承数据的时频特征图作为网络的输入。

综上所述,本文首先利用CWT变换提取轴承的时频退化特征,然后,建立了使用可变形卷积、普通卷积、注意力机制与残差结构的ADRN预测网络,最后,为了对网络的训练加以约束,构建了动态损失函数。

1 基础工作

1.1 数据集介绍

本文使用IEEE PHM2012轴承数据集[10]来进行实验。PHM2012数据由IEEE可靠性协会和法国FEMTO-ST提供,在PRONOSTIA平台(图1)上进行,该平台通过传感器收集来自水平和垂直方向的振动加速度信号,传感器每10 s收集1次0.1 s的数据(频率25.6 kHz)。PHM2012采集了3种不同转速负载下17个滚动轴承的数据,其测试集与训练集的划分如表1所示。

表1 PHM2012数据集中训练集与测试集划分

图1 PRONOSTIA实验台[10]

1.2 评价指标

本文使用预测误差评价预测效果,对模型整体的精度使用分数(S)作为评价标准。

1) 预测误差:

(1)

式中:E为预测误差;ARUL为轴承的真实剩余寿命;PRUL为轴承的预测剩余寿命。

2) 分数:

在实际的生产生活中,欠预测(E>0)优于过预测(E<0),因此在后续的实验中,使用评价指标分数来描述这种影响,第i个轴承的评价分数Ai为

(2)

Ai越接近1,预测的精度越高。在同精度下,欠预测得分是高于过预测的。为评价模型的整体精度,将所有N个测试轴承的评价指标求平均得到模型的评价分数,记作S。

(3)

1.3 可变形卷积

相较于可变形卷积,普通卷积固有的几何结构对未知形状的数据特征建模存在不足。以图2为例,在对时频图进行卷积计算时,普通卷积的卷积核为固定的矩形,而可变形卷积则可以通过一个偏移量来适应特征的几何形状。

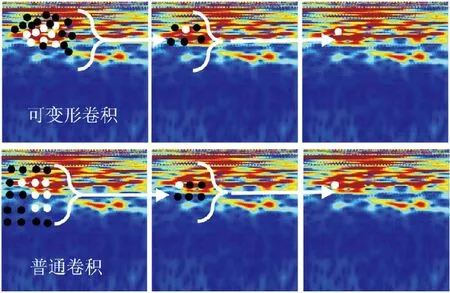
图2 可变形卷积与普通卷积示意

普通卷积与可变形卷积的计算输出定义如下。

1) 普通卷积计算。使用规则网格G对二维特征图采样时,对于一个膨胀率为1的3×3卷积核而言,G可表示为

G={(-1,-1),(-1,0),…,(0,1),(1,1)}

(4)

其中,G的每个元素代表卷积核的所有位置相对于中心位置的偏移量。

因此对于采样中心位置为p0的普通卷积而言,其计算输出为

y(p0)=∑pn∈Gw(pn)·x(p0+pn)

(5)

式中:pn为采样点位置;w(·)为卷积得到的当前位置权值;x(·)为输入对应的位置值。

2) 可变形卷积计算。对于可变形卷积而言,通过在G上增加偏移量得到式(6):

y(p0)=∑pn∈Gw(pn)·x(p0+pn+Δpn)·Δmn

(6)

式中:Δpn为采样点位置pn的偏移量;Δmn为权值调制参数,Δmn∈[0,1]。

Δpn与Δmn通过额外的卷积层计算得到,额外卷积层在计算时所使用的学习率为原有卷积层的0.1倍,Δpn与Δmn的初始值分别为0和0.5。

2 基于可变形卷积的轴承RUL预测方法

为了对滚动轴承进行准确地RUL预测,本文构建了基于图像化轴承时频特征数据与深度学习网络的预测方法,如图3所示。该方法由数据预处理、ADRN预测网络和RUL预测3个模块组成。

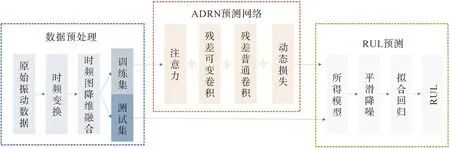
图3 轴承RUL预测方法流程

数据预处理模块:①利用CWT提取轴承的时频特征,并生成时频图;②使用双行性差值对原始的轴承时频图进行降维;③将每个采样时刻水平与垂直方向的时频图利用通道拼接构建成新的轴承退化数据。

ADRN预测网络模块:ADRN预测网络主要由注意力、残差可变卷积与残差普通卷积构成,并使用动态损失减少网络训练中的异常值。①在轴承深层退化特征提取过程中,注意力机制为初级退化特征分配贡献权值;②使用残差可变卷积与普通卷积自动提取轴承深层退化特征;③在网络训练过程中利用由MSE与RMSLE组成的动态损失函数约束预测网络;④通过全连接层对深层退化特征下采样,并使用Tanh激活函数计算并输出健康因子。

RUL预测模块:①将预处理后的数据测试集输入训练好的预测网络,得到预测健康因子(HI);②为去除HI中的异常值并加强轴承的退化趋势,使用Savitzky-golay滤波器平滑预测HI;③利用多项式函数精确拟合平滑后的HI,得到轴承的预测RUL。

2.1 数据预处理

当滚动轴承运行到生命后期,由于脉冲变载荷原因造成轴承处于非平稳的状态,因此收集到的轴承原始振动信号也是非平稳、非线性的[11],不能清晰和准确描述轴承的退化特征,降低了RUL预测效果。因此本文通过CWT提取轴承的时频故障特征图。以训练集Bearing1-1第2600个采样时刻的原始振动数据为例,轴承原始振动数据与CWT时频如图4(a)和(b)所示,轴承时频特征图中的故障特征更为清晰丰富。

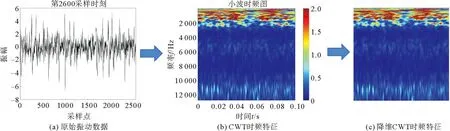
图4 数据预处理过程

进行预测网络训练时,时频图的尺寸过大会影响到网络训练的效率。因此本文首先对原始CWT时频图(840×840×3)使用双线性插值将其缩小到适合处理尺寸(224×224×3),如图4(b)和(c),最后将得到的每一采样时刻水平与垂直方向的时频图利用通道拼接构成新的退化数据特征(n×224×224×6,n为采样时刻)。

2.2 ADRN预测网络

本文的预测网络具体结构如图5所示,其中,降级卷积降采样层由1层7×7的二维卷积与1层二维全局平均池化组成;注意力结构由通道与空间注意力组成;可变卷积层则是由可变卷积块与下采样可变卷积块组成。

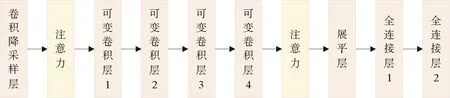
图5 ADRN预测网络结构

2.2.1 注意力

预测网络在训练时,首先将输入尺寸为224×224的时频退化数据通过卷积核为7×7的二维卷积进行降采样,得到退化特征(F);之后由通道与空间注意力为退化特征重新分配权重;最后,在全连接层将深度退化特征计算为健康因子HI之前,使用通道与空间注意力为深度退化特征(F′)重新分配权重,使网络在特征提取时关注到更为重要的退化特征。具体流程如图6所示。

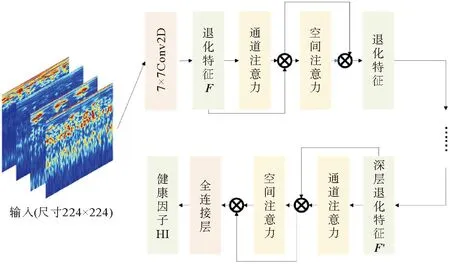
图6 注意力机制

退化特征中的每一个通道都代表一个特征的表达,因此,为了在特征提取时充分利用特征图中的有效特征数据,使用通道注意力为特征图中的每一个通道赋予一个数值,将该数值与对应的特征图元素进行相乘计算,得到加权后的退化特征。为确定特征图不同空间方位重要程度,通过空间注意力的像素级的计算,可以得到特征图中每一通道上的每一像素值的权重。

2.2.2 深度残差可变卷积

轴承的CWT时频图中不同特征之间的边界划分较为复杂,而且时频图中的特征形状是不规则的,如图4(b)所示。因此,为了获得更为准确的特征信息,本文利用可以适应特征的几何形状可变形的二维卷积构建了可变卷积层,而构成可变卷积层的可变卷积层块与下采样可变卷积块的结构如图7所示。

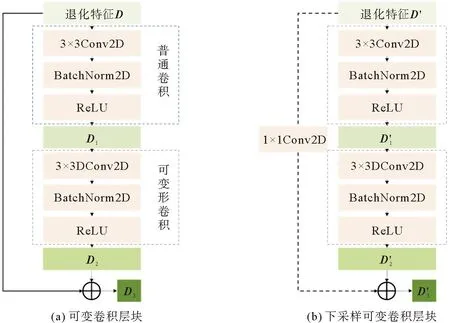
图7 可变卷积层

在可变卷积块中,首先由普通卷积对退化特征D进行3×3的卷积计算,并由批标准化(BachNorm2D)与激活函数(ReLU)进行处理得到退化特征D1;然后使用卷积尺寸为3×3的可变卷积计算D1,得到退化特征D2;最后在残差结构中D与D2逐点相加,得到退化特征D3。较于可变卷积块,下采样可变卷积块,则是在残差结构中加入了1×1的二维卷积,对特征进行升维和下采样处理。

可变形卷积计算时会对采样点的权重再次分配,因此在可变卷积块与下采样可变卷积块中,并没有加入空间与通道注意力。但是因为可变形的卷积计算和采样点权重分配会成倍地增加模型参数,因此本文的卷积计算并没有全部使用可变形卷积,而是加入了普通卷积来增加网络计算复杂度。同时为避免网络深度增加造成梯度的不稳定,在网络构建时加入了残差结构。

2.2.3 动态损失

滚动轴承在退化过程中经常出现瞬时突发故障,而在网络训练过程中,这些突发故障数据有可能造成影响网络精度与稳定性的异常值出现;并且随着网络的加深,计算复杂度的上升,在网络训练过程中难免出现异常值。而为了减少网络训练时异常值影响,本文将MSE与RMSLE损失函数相结合,当训练集的真实值与预测值的差小于阈值(σ)时,网络利用MSE损失函数训练,而当真实值与预测值的差大于阈值(σ)时则使用RMSLE损失函数,即

(7)

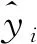
当面对较小的训练误差时,MSE可以有效地将网络收敛到最小值;而当面对较大的训练误差时,RMSLE因对数的计算所以几乎不受影响。

为了对比不同阈值设置下的网络训练结果,本文分别设置阈值0.01,0.05,0.1,0.5,1和5进行对比训练。在训练过程中,测试集数据设置退化标签用以监督,其定义为:当前运行时刻/总运行时间,分布于0～1之间,代表了轴承运行到此时的损坏程度,0为完全健康、1为完全失效,并使用Adam优化器、学习率为0.001、批量大小为4、训练周期为50作为网络训练的超参数设置。PHM2012中所有训练集的平均误差(MAE)与确定系数(R2)的平均值如表2所示。

表2 不同阈值设置下的训练结果

由表2可以观察到,当阈值设置为0.01时网络训练效果较差,而其余阈值的设置下网络训练结果非常相近,当阈值为0.01时网络的损失函数为RMSLE。为了进一步选取合适的阈值设置,本文使用测试集轴承Bearing1-6(退化过程存在异常故障)对比了不同阈值设置下的HI预测结果(图8)。

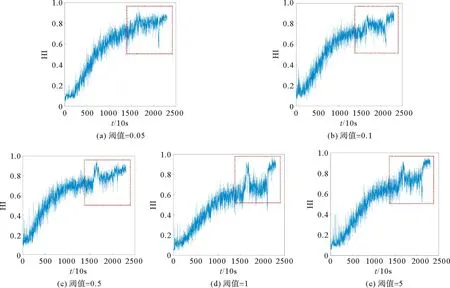
图8 不同阈值设置下的Bearing1-6的预测结果

由图8可以看到,5种不同阈值设置下的轴承退化趋势较为相似,但是在异常故障发生时(红色方框所标记的区域)只有阈值为0.05时预测结果的波动较小。因此,本文选取阈值为0.05的动态损失作为本文网络的损失函数。

2.2.4 HI预测

可变形卷积层与注意力将轴承退化数据计算为深度退化特征后,首先使用展平层将退化特征转变为一维数据;然后由全连层对一维的退化特征进行下采样,并由tanh激活函数输出健康因子HI。

2.3 HI平滑与RUL预测

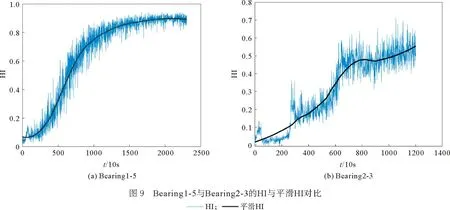
在得到轴承的预测HI后,为了避免HI的分布震荡导致预测结果不准确,本文首先使用了Savitzky-golay滤波器对预测HI进行平滑处理;之后利用多项式拟合平滑后的HI,得到回归函数并计算出轴承的预测RUL。图9为Bearing1-5和Bearing2-3的原始预测HI与平滑后的HI对比,可见经过平滑后预测HI中的异常值被剔除,轴承整体退化趋势更加清晰,减少了后续HI拟合的误差。

测试集中轴承在不同工况下的振动表现与故障类型是不同的,因此它们的退化趋势也是不同的。如果对不同轴承使用相同的拟合函数来拟合回归HI,会造成欠拟合现象,无法有效且准确地预测RUL。因此,本文拟合过程中,选择均方根误差(RMSE)落在[0.01～0.04]的多项式函数作为每一个轴承的最终拟合回归函数,图10为3种不同工况下的轴承拟合回归曲线。由图10可以看出,本文所选用的多项式拟合函数可以较好地拟合HI。图10红框中为拟合曲线纵坐标为1时(轴承完全失效)的波形,其中图10(a)与图10(b)非常符合整体的退化趋势,因此,得出来的预测结果更加真实地反应了本文模型的预测能力。图10(c)的退化趋势较为复杂,而本文的拟合回归函数也可以有效地拟合HI,说明本文模型的预测能力较强。

3 实验与结果分析

3.1 消融实验

为了证明本文提出的可变形卷积与注意力机制在轴承RUL预测任务中的有效性,设计了4个消融实验:a.普通卷积+无注意力;b.普通卷积+有注意力;c.可变卷积+无注意力;d.可变卷积+有注意力。

在相同的硬件环境下4个网络对3种不同工况下的轴承预测结果如表3所示。实验d在Bearing1-3、Bearing1-4、Bearing2-5、Bearing2-6上预测误差的绝对值最小,意味着预测的RUL更接近于真实RUL;而在Bearing1-3、Bearing1-4、Bearing2-5、Bearing3-3上实验d的预测均为欠预测,意味着预测结果更贴合实际预测需求。因此,消融实验的结果证明可变卷积计算表达能力要强于普通卷积,预测结果更接近真实寿命。

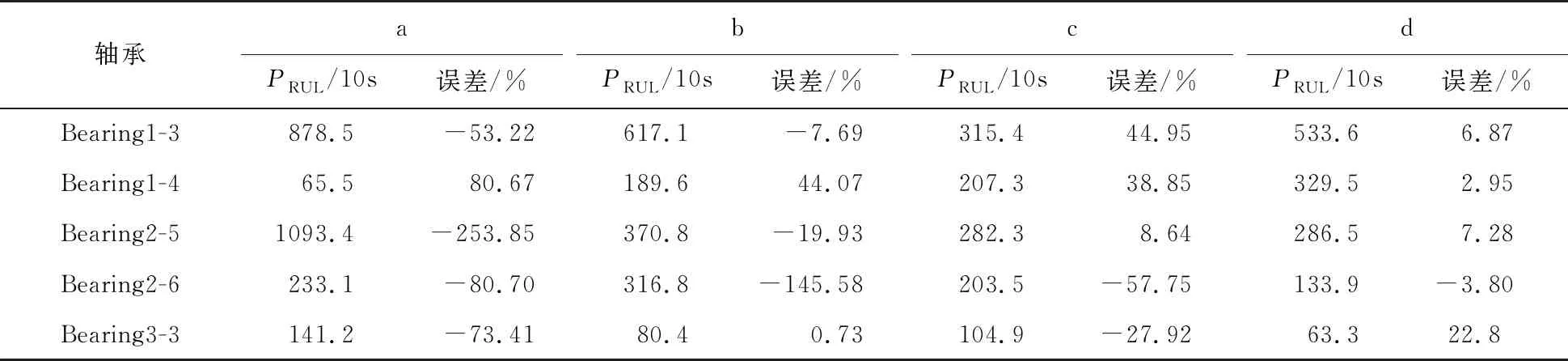
表3 消融实验预测结果

3.2 对比实验

为了证明本文提出方法的有效性,在PHM2012数据集上使用预测误差与评价分数作为评价指标,与已被证明有效的4种方法[12-15]进行了结果对比,如表4所示,由轴承真实RUL、本文预测的RUL、每个轴承预测误差(E)计算得到平均预测误差和预测分数S。文献[12]首先将原始数据处理为时频谱图,之后利用残差神经网络与时间卷积神经网络(R-T)进行退化建模;文献[13]利用长短期记忆循环网络构成的编码解码结构预测模型(LSTM-ED)进行RUL预测;文献[14]利用模态分解提取其中具有代表性的模态分量作为特征数据,使用循环神经网络(EMD-RL)进行预测建模;文献[15]为PHM2012挑战赛获胜算法(PHM2012)。

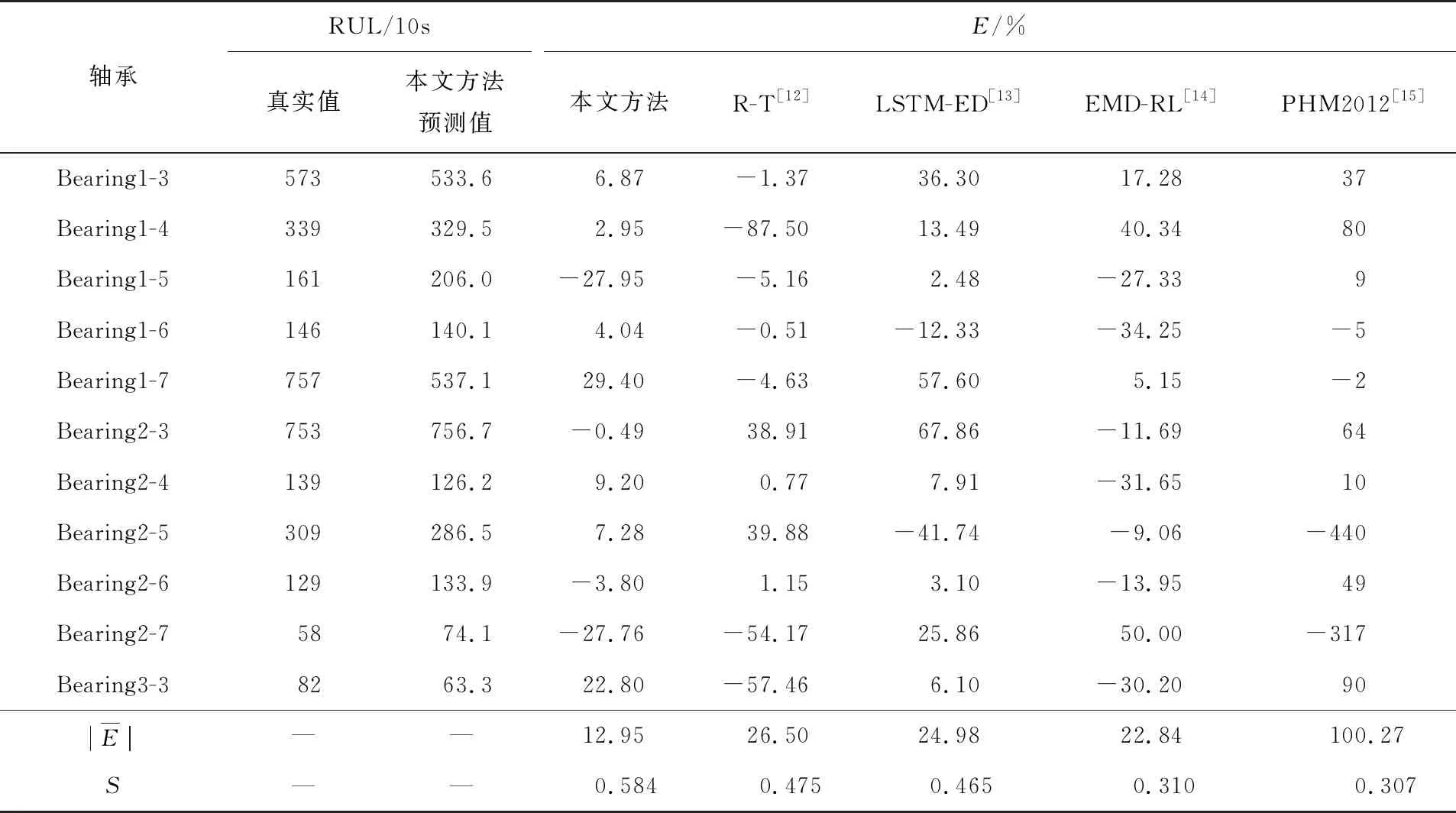
表4 PHM2012数据集中不同方法的预测结果对比

通过表4可以看出,与已被公开证明的方法相比,本文所提出方法的预测平均误差要小于其他方法,而且评价分数也要高一些,证明本文方法可以有效进行剩余寿命预测。

4 结论

本文在建立轴承预测网络时利用可变形卷积取代了部分普通卷积,并通过注意力机制与动态损失函数提升了预测网络的复杂度与稳定性。在PHM2012数据集中,与其他方法的预测结果相比,预测精度有较大提升。