基于改进运动原语生成的陆空两栖机器人Kinodynamic A＊算法

徐彬，孙恒飞，唐寿星，王雨桐，张旺旺，艾田付

（1.北京理工大学 机械与车辆学院，北京 100081；2.北京理工大学 重庆创新中心，重庆 401135）

陆空两栖机器人具备空中机器人的强机动能力和地面机器人的长续航能力的综合优势，在搜救、巡检、快递等长距离作业任务的应用场景下备受关注.应用场景的复杂性对陆空两栖机器人提出了无人化、智能化的要求，机器人需要完成包括感知、定位与建图、路径规划、运动控制等模块的协调工作.路径规划作为智能化的关键模块，其主要作用在于找到一条从起点到终点的无碰撞安全路径，并实现路径时间、距离、能耗等代价项的优化.

在已落地于实际场景的无人车算法里[1-2]，常见路径搜索算法分为基于图搜索的路径规划、基于采样的路径规划、人工势场法等.轨迹优化算法有B 样条优化、五次多项式优化、螺旋曲线优化等[3].由于移动机器人受到实际运动约束，大多算法需要在A*或RRT 算法的基础上进行改进，以满足实际运动需要.如PIVTORAIKO 提出state lattice planning[4]，通过局部状态之间的连接生成可行路径，在可行路径基元组成的搜索空间上进行图搜索，从而保证了规划路径的可行性；DOLGOV 提出Hybrid A*[5]，通过捕获A*离散节点中车辆的连续状态，使用车辆运动学生成的运动轨迹代替A*算法中的节点转移，从而保证了路径的运动学可行性；WEBB 提出 Kinodynamic RRT*[6], 基于状态空间采样并引入最优控制计算代价项，用符合动力学特性的曲线代替直线连接到最近节点，从而保证路径更加满足动力学约束.这些算法弥补了基础搜索算法生成的路径不符合运动约束的问题，但仍存在一些不足：State lattice planning 基于控制空间的采样无法精准采样到给定状态，基于状态空间的采样需要求解OBVP 问题来求得轨迹；Hybrid A*具有分辨率最优性，但在大地图下复杂度过高；Kinodynamic RRT*概率完备，渐进最优，但同样需要求解OBVP 问题来求得轨迹.

相较于单模态的路径规划，陆空两栖机器人路径规划更具挑战且备受关注[7]，其需要考虑陆空两种不同模态下的运动学、动力学约束及运动代价差异，并要求模态切换过程顺滑过度[8].Kinodynamic A*[9]由于其在运动原语的生成过程和剪枝过程中便考虑了约束，能很好满足以上需求.Kinodynamic A*使用离散加速度、时间作为状态空间控制输入来生成运动原语，通过给终点在空中节点的运动原语施加额外能量代价项表征飞行运动代价，通过一系列工程优化加快了算法速度实现快速规划[10]，在被动轮式四旋翼陆空机器人上表现出优异性能，在地面行驶中实现了约7 倍的节能[11].但其算法仍然存在以下问题：一是算法使用统一的离散控制输入导致生成的运动原语一致，未能体现陆、空模态运动差异；二是算法使用统一的速度上限进行剪枝，不合理地限制了空中模式的运动能力；三是轨迹优化时采用一致的速度、加速度代价，以地面模式运动能力为标准时限制了空中模式运动潜力.上述问题导致算法无法充分发挥陆空两栖机器人的强机动能力.

为充分发挥陆空两栖机器人的机动性优势，文中采用改进运动原语生成的陆空两栖机器人Kinodynamic A*算法.具体来说，基于动力边界离散加速度输入，生成差异化运动原语表征陆、空两种模态的运动能力；基于速度边界对运动原语进行剪枝以满足运动约束；修改优化代价函数，满足陆、空模态下运动的安全性及机动性.最后在仿真场景下验证改进后的Kinodynamic A*算法的机动性及节能性.

1 路径搜索

陆空两栖机器人路径搜索基于Kinodynamic A*算法.该算法在障碍物占据栅格地图中，搜索一条符合运动学、动力学约束的无碰光滑路径.Kinodynamic A*搜索过程与A*算法相似，在A*的基础上，依据状态空间方程生成运动原语，剪枝满足每个栅格仅保留一个节点，求解最优化问题以获取启发项.本节在Kinodynamic A*的基础上，改进Kinodynamic A*算法，使其运用于陆空两栖机器人路径搜索，通过控制状态空间方程加速度输入，差异化生成陆、空模态运动原语.

1.1 算法流程

改进Kinodynamic A*算法流程图如图1 所示.

1.2 改进运动原语生成

文中使用时间参数化的五次多项式函数表征机器人x、y、z三个独立维度的轨迹，即

设机器人的状态量x=，设控制量u=，使用状态空间方程来描述系统

状态空间方程表明文中可以通过输入控制量u=来控制机器人的状态量x=[px py pz;vx vy vz]，即输入控制量加速度a来控制状态量位置p和速度v.在给定机器人的当前状态x(t0) 和控制输入u(τ)的情况下，考虑时间t的向前积分，由状态方程的解

即

由此获取下一个节点的运动状态，从而生成运动原语.

在改进运动原语生成时，输入为一系列离散加速度，在每个方向上等分为每个离散时间 τ下段生成(2k+1)3个运动原语.陆空两栖机器人在地面模式下及空中模式下可提供的动力不同，在空中模式下可提供更大的加速度输入，应具有以下形式：

改进前后的运动原语生成结果对比如图2 所示，通过控制状态空间方程加速度输入，差异化生成了陆、空模态运动原语.其中绿色带星号运动原语为在改进后空中模式的运动原语，黑色为未改进前陆、空模态使用一致加速度时所产生的运动原语.经过改进，空中模式下产生的运动原语将探索更广的范围，产生更积极的速度和加速度，使得陆空两栖机器人能充分发挥空中模式下优越的机动能力.

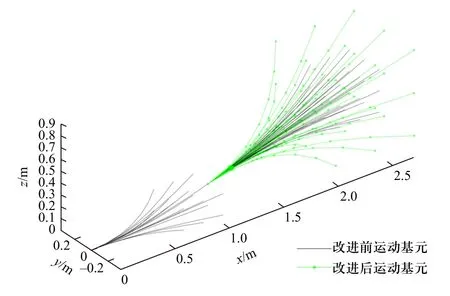
图2 改进前后的运动原语生成结果对比Fig.2 Comparison of generation results of motion primitives before and after improvement

1.3 改进剪枝

剪枝以保证搜索算法的效率，Kinodynamic A*在每个栅格点内仅保留一个终点状态位于栅格内的运动原语，此外对于终点速度超过运动能力上限的运动原语进行剔除.Kinodynamic A*算法对于陆、空模态下的运动原语采用一致的终点速度上限进行剪枝，这在保证了陆空两栖机器人规划路径安全的同时带来了规划路径过于保守的问题.特别是空中模式下的剪枝，若采用与地面模式下相同的速度上限，将极大降低机器人的机动能力.改进后的剪枝方法依据机器人运动模式使用不同的终点速度上限，具有以下形式

由运动原语终点状态的高度pz区分机器人的运动模式，文中保留终点状态符合速度上限的运动原语，其中空中模式下拥有更大的速度上限，以表征空中模式下的强机动性.

1.4 边界转移代价和启发项设置

构造边界转移代价及启发项函数来表征陆空两栖运动控制、时间及能耗代价.在计算边界转移代价时，对终点位置位于空中的运动原语乘以飞行能耗系数表示飞行较于地面行驶能量损耗的倍数，对高度爬升的运动原语，增加额外代价表示模态切换过程中的额外能量损耗.综合考虑时间和控制的代价量，实际代价函数定义为

其中u(t) 表示控制量；g(u(t))表示控制代价； ρ用来控制时间的权重.g(u(t))定义如下：

genergy_cost为地面行驶能耗代价；kf为飞行能耗系数；fswitch_cost为模态切换飞行代价.当给出离散化控制量u(t)=ud，持续时间t=t，运动状态完成转移，终点状态为pz=p，计算得g(u(t))=g，得到运动原语的代价表示为

由起始状态到节点状态，经历了个运动原语，则

启发项设置基于庞特里亚金最小值原理[12]：在控制向量u(t)受约束的情况下，求解从状态xcurrent到终点状态xgoal的最优控制,使得目标函数J(T)取极小值J*(T)，这里的J(T)文中定义为

求解为

此外，考虑模态切换过程，xcurrent的状态量pz决定当前飞行状态，对于最终目标xgoal为地面模式的目标函数，修改启发项为

理论上，飞行需要克服自身重力做功，而行驶主要克服地面摩擦力做功，因此飞行能耗远高于地面行驶能耗，飞行能耗系数kf约为15～20，对应不同载荷下的能耗比.这使得算法趋向于选择一条地面的行驶路径，除非当绕路通过障碍物的代价远超模式切换后飞越障碍物的代价.

2 轨迹优化

由于路径搜索未将离障碍物的距离纳入考虑，启发项为达到能量优化的目的，生成的路径经常紧贴障碍物，轨迹优化的主要目的在于平滑路径、使之远离障碍物并充分发挥机器人的机动性能.由于陆、空模态下陆空两栖机器人的运动约束不同，文中在构造优化代价函数时，在空中段路径使用更大的障碍物距离安全阈值以保证安全性能；给予空中模式下更大的速度、加速度阈值以保证机动性能；在地面段路径加入曲率约束以保证跟踪性能.

2.1 模式切换决策

在不同模态下，路径的轨迹优化代价函数形式相似但参数不同，故轨迹优化前需要对路径进行分段.首先通过均匀离散时间采样获取路径点，参数化路径为具有控制点序列S={Q0,Q1,···,Qtotal} 的3 阶均匀B 样条曲线.根据控制点高度进行模式切换决策，将路径分为地面行驶路径、陆空切换-起飞路径、空中飞行路径和陆空切换-降落路径，对应机器人模式为以下四种：地面、起飞、空中飞行、降落.

设置模式切换高度阈值为pthr，根据控制点高度pz大小分为地面行驶的控制点集合Sg与空中行驶控制点集合Sf，表述为：

根据路径连续性划分各段路径控制点集合.设Sg有m段地面行驶路径，Sgi为第i 段连续的地面路径控制点集合，共有gi_count 个控制点，其首尾控制点连接起始、终止状态或空中路径控制点.设Sf有n段地面行驶路径,Sfi为第i 段连续的空中路径控制点集合，共有fi_count个控制点，其前后连接地面路径控制点.表述为

机器人运动过程中有限状态机如图3 所示.

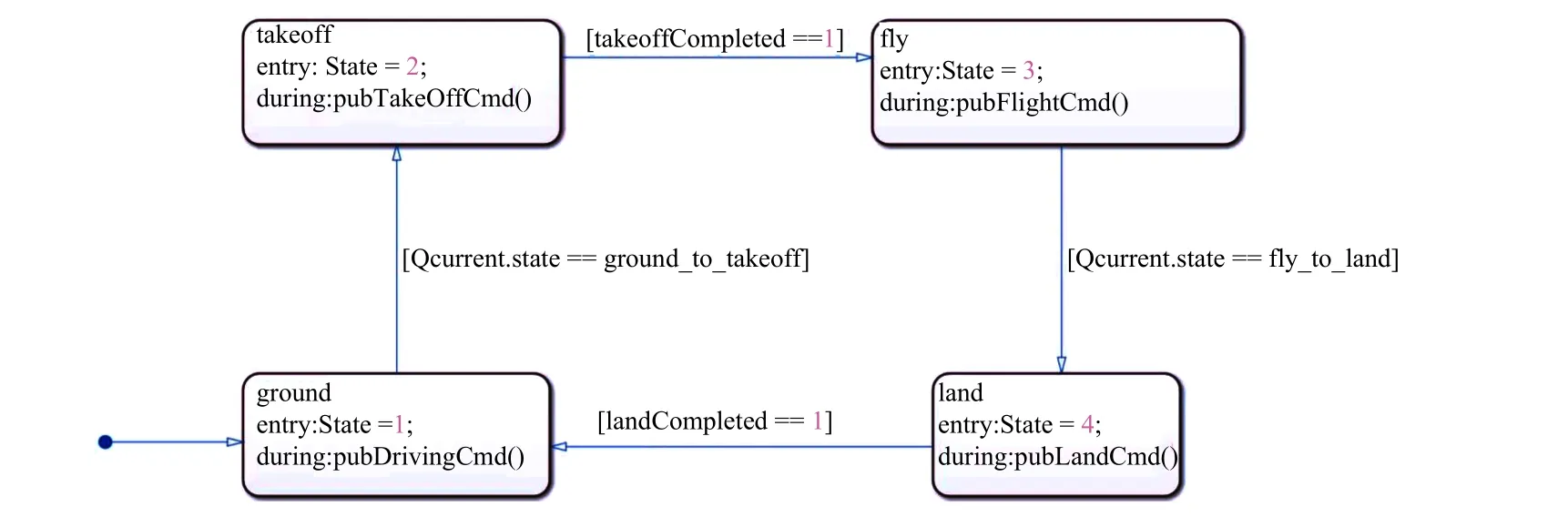
图3 陆空两栖机器人运动状态机Fig.3 Movement state machine of hybrid aerial-ground robot

① 文中认定地面模式切换起飞模式的逻辑为：当前控制点Qi为地面控制点且该点后连续n个序列点为空中控制点时，此点为地面模式到起飞模式切换点，表述为

② 起飞模式完成后无人机自动切换为空中模式.

③ 文中认定空中模式切换降落模式的逻辑为：当前序列控制点为空中控制点且该点后连续n个序列点为地面控制点时，此点为空中模式到降落模式切换点，表述为

④ 降落模式完成后无人机自动停桨，并切换为地面模式继续行驶，如图4 所示.

图4 模式切换决策示意图Fig.4 Schematic diagram of mode switching decision

对于一段轨迹Sgi={Qgi0,Qgi1,···,Qgi gi_count-1}或Sfi={Qfi0,Qfi1,···,Qfi fi_count-1}，为方便后续轨迹优化的描述，其控制点统一表述为

2.2 轨迹优化

轨迹优化使用分段B 样条曲线拟合轨迹，结合B 样条控制点跃度、欧氏距离场、速度加速度约束及曲率约束的梯度信息，通过优化B 样条曲线控制点来优化轨迹的平顺性、安全性及机动性.

设置代价函数为

式中：fs为平滑度代价；fd为障碍物距离代价；fv、fa分别为速度、加速度代价；fc为曲率代价；λs、λd、λf、λc为各代价的权重.

①平滑度代价

平滑度可以通过跃度（加速度对时间的导数）来进行量化分析，表示为

②障碍物距离代价

障碍物距离代价表示为控制点离最近障碍物距离的代价，通过此项排斥控制点使之远离障碍物：

这里d(Qsi j) 为控制点到最近障碍物距离，Fd(d(Qsi j))为单个控制点的障碍物距离代价函数，dsithr为障碍物距离安全阈值.对于空中轨迹段，考虑到壁面效应，文中给予相对地面轨迹段更大的障碍物距离安全阈值.

③速度、加速度代价

速度、加速度代价用于对超过约束的速度、加速度施加惩罚：

这里vsi j、asi j分别为控制点速度与加速度，Fv(vsi j)、Fa(asi j)分别为单个控制点的速度代价与加速度代价函数，vsithr、asithr分别为控制点速度与加速度阈值.考虑到飞行模式下机器人有更强的运动能力，为更好发挥其强机动性的优势，文中给予相对地面模式更大的速度阈值.

④曲率代价

履带车辆于地面运动时速度方向为偏航角方向，其正逆运动学模型约束了速度、角速度大小.若是轨迹曲率过大，履带车辆执行转弯时将产生较大跟踪误差.使用曲率代价项fc来限制地面轨迹的曲率:

其中Csi j为控制点Qsi j的曲率，定义为

文中给予空中模式下λc=0表征空中模式下飞行器可以规划大角度的转弯且能顺利完成跟踪而不需考虑额外代价.给予地面模式下λc＞0表征地面模式下履带车辆需考虑曲率限制，减少控制时的转弯跟踪误差.

3 试验结果与分析

3.1 试验平台及试验设置

使用涵道-履带复合式陆空两栖机器人进行试验：硬件平台选择上，使用D435i 作为深度传感器，使用Jetson Xavier NX 板载计算机作为中心计算单元，使用烧录PX4 固件的雷迅创新V5+作为飞控.陆空两栖机器人如图5 所示，其中相机前置，飞控及计算单元已安置在中心碳纤维板盖下，机器人尺寸为0.6 m×0.6 m×0.1 m.陆空两栖机器人采用双模式一体化设计，飞行模式采用四涵道推进方式，行驶模式采用履带式推进方式.

图5 陆空两栖机器人Fig.5 Hybrid aerial-ground robot

软件平台布置在Ubuntu18.04 操作系统上，使用ROS 进行节点间通信.算法代码使用C++11 实现，使用非线性优化库nlopt 求解轨迹优化问题，软件框架如图6 所示.

图6 软件框架Fig.6 Framework of software

算法参数设置表1 所示.

表1 算法参数Tab.1 Simulation parameters

搭建仿真场景及对应实际场景，在确保算法可行的情况下再上实机进行试验.其中场景设定如图7 所示，场景宽6 m、长11.4 m，外围设有安全网.场景内设有立方体状1.2 m 高障碍物，其中在6.6 m处设有横跨障碍物完全封死地面通行.在已知环境下的任务为：给定目标位置，机器人需规划出一条从当前位置到目标位置的安全无碰撞轨迹，必要时实现陆空两栖切换以跨越障碍物.

图7 仿真及试验场景Fig.7 Simulation and experiment scenarios

图7(a)为机器人工作空间在rviz 中的表示，其中start 点为坐标原点.由于机器人有大小及形状，为便于规划中的避障判定，常将机器人转换为质点并将障碍物按照机器人体积进行膨胀，从而生成配置空间.按照机器人的尺寸及其运动可能的姿态将横纵向障碍物皆膨胀0.45 m，垂向膨胀0.2 m（飞机为扁平状且无法做出大角度俯仰或滚转姿态，其垂向最大间距认为不超过0.4 m），配置空间在rviz 中的表示如图7(b)所示.

图7(c)和(d)为实际搭建场景展示，(c)处场景下为避开前方障碍物机器人需做出左转或右转决策，(d)处场景下为越过障碍物，机器人需做出模式切换决策并飞跃障碍物，仿真场景与实际场景障碍物设定一一对应.

3.2 试验结果分析与对比

与同样使用Kinodynamic A*作为搜索算法的陆空两栖运动规划器TIE[11]做对比，其中除算法运动原语及轨迹优化函数改进部分，其余部分参数如栅格分辨率、离散时间分辨率等设置一致以在同等条件下做对比.设置障碍物栅格地图及Kinodynamic A*算法栅格分辨率为0.2 m，设置运动原语时间 τ为0.5 s，加速度分辨率为amax/3，时间分辨率为τ/2 ，其余参数设置为表二中数据，得到的规划路线对比如图8所示.

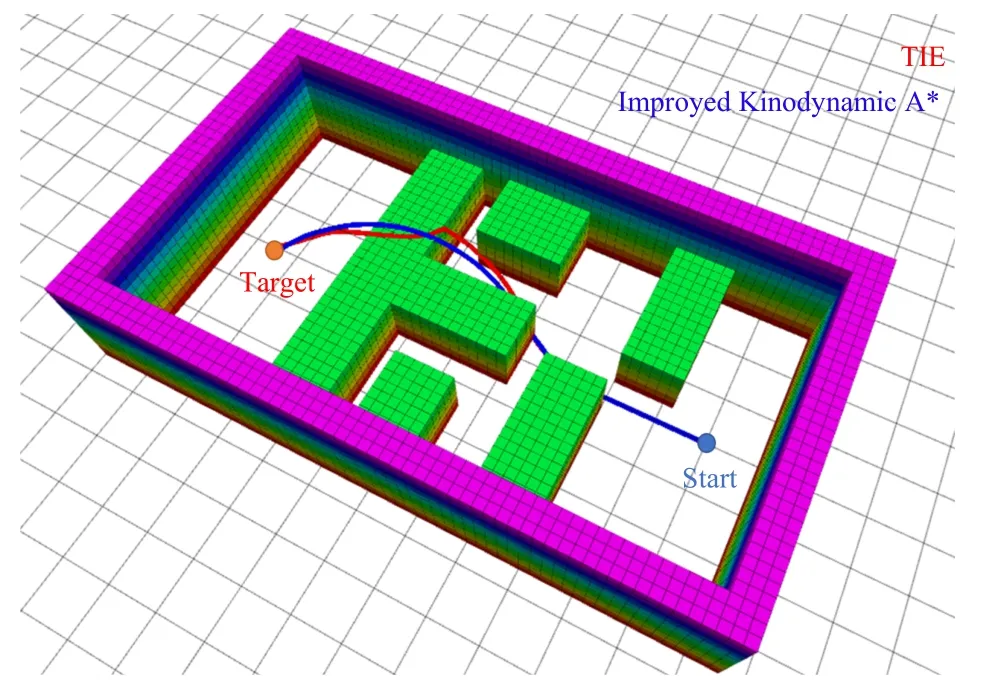
图8 规划路径对比Fig.8 Comparision of planned path

两种算法都实现了陆空两栖规划，但在不同场景下及不同参数下两种算法的性能表现不同.在上述场景下，路径总时间、飞行平均速度、路径总代价、算法运行时间在不同运动原语时间下呈现如下图9.

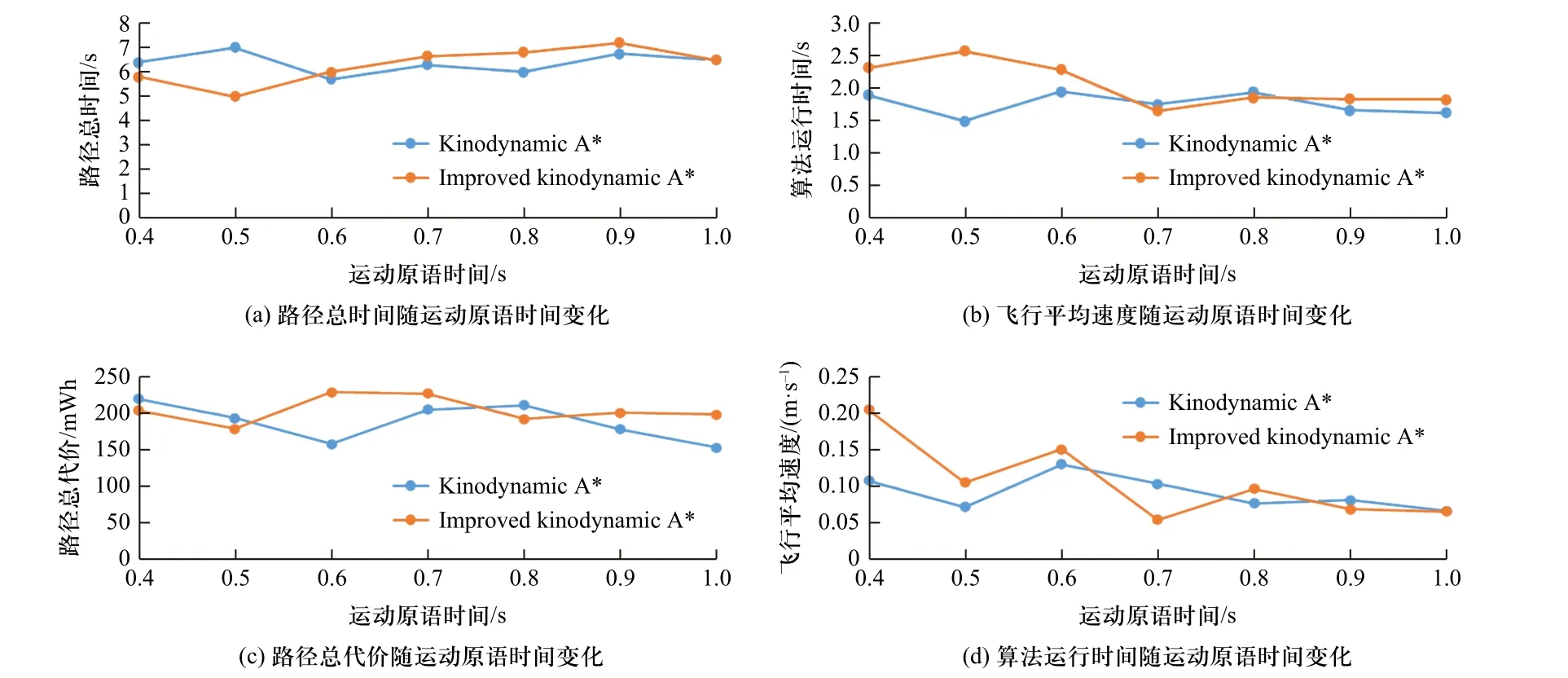
图9 各项性能随运动原语的变化Fig.9 Changes of various performances with motion primitives

当运动原语时间为0.1 s、0.2 s、0.3 s 时，算法由于运动原语时间过短，未能跨越栅格从而未能找到路径.运动原语时间设置为0.4 s 及0.5 s 时，本算法的路径总时间、飞行平均速度、路径总代价略微优于TIE，但算法运行时间略差.在超过0.5 s 的运动原语时间下，算法性能表现不如TIE.这与Kinodynamic A*本身性质有关：空中模式下较大的控制量加运动原语时间导致运动原语生成时非常容易跨越一些栅格，加上运动原语剪枝，导致了一些可能运动状态的丢失，从而生成的路径并非最优.

路径规划算法的性能依赖于地图场景，本算法的最大优势在于发挥陆空两栖机器人在空中运动的机动性.故搭建图10 所示场景，进行进一步分析.

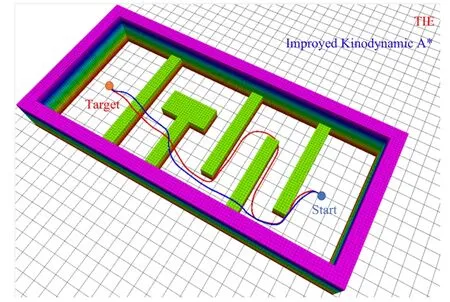
图10 飞过障碍物需求多的场景下规划路径对比Fig.10 Comparison of planned paths in scenarios with high demand for flying over obstacles

图10 为在大场景下规划路径对比，其中参数为表2 中参数，设置运动原语时间 τ为0.5 s，时间分辨率为 τ以加快搜索速度.可以发现改进后的Kinodynamic A*算法在第一个转角处决策与TIE 不同，由于发挥了机器人空中机动性优势，算法选择直接飞过障碍物.改进后的算法将路径总时间从20.5 s 降低到了12 s.路径总代价由524 mWh 降低到420 mWh.由于路径遍历了更少节点，算法运行时间也从0.224 s降低到0.166 s，在此场景下充分体现了算法优越性.

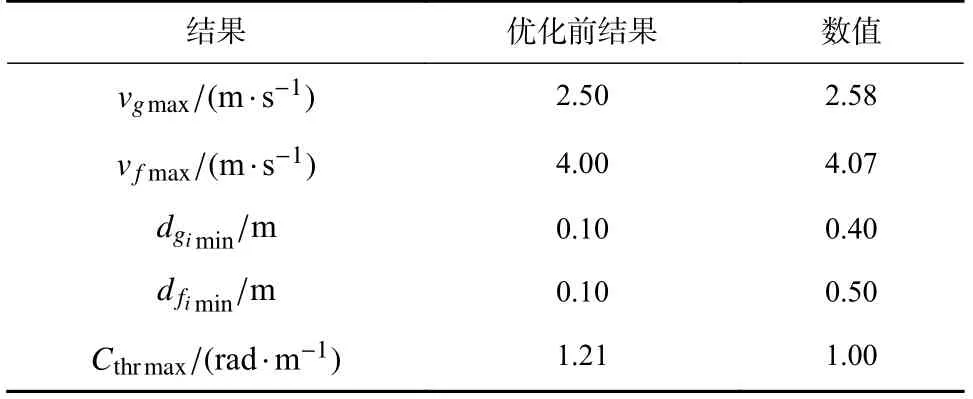
表2 轨迹优化前后结果Tab.2 Results before and after trajectory optimization

在此场景下，路径总时间、飞行平均速度、路径总代价、算法运行时间在不同运动原语时间下呈现如下图11.

图11 各项性能随运动原语的变化Fig.11 Changes of various performances with motion primitives

当运动原语时间为0.1 s、0.2 s 时，两种算法皆未能找到路径.当运动原语时间为0.3 s 时，TIE 规划失败，改进后的Kinodynamic A*算法由于机动性更强而成功规划出路径.当运动原语时间设置为0.4 s 至1.0 s 时，本算法的路径总时间、飞行平均速度、路径总代价、算法运行时间皆优于TIE.其中路径总时间平均降低6.7 s，飞行平均速度平均提升54.1%，路径总代价平均降低22.00%，算法运行时间平均降低0.069 s.

B 样条优化前后轨迹对比如图12 所示.

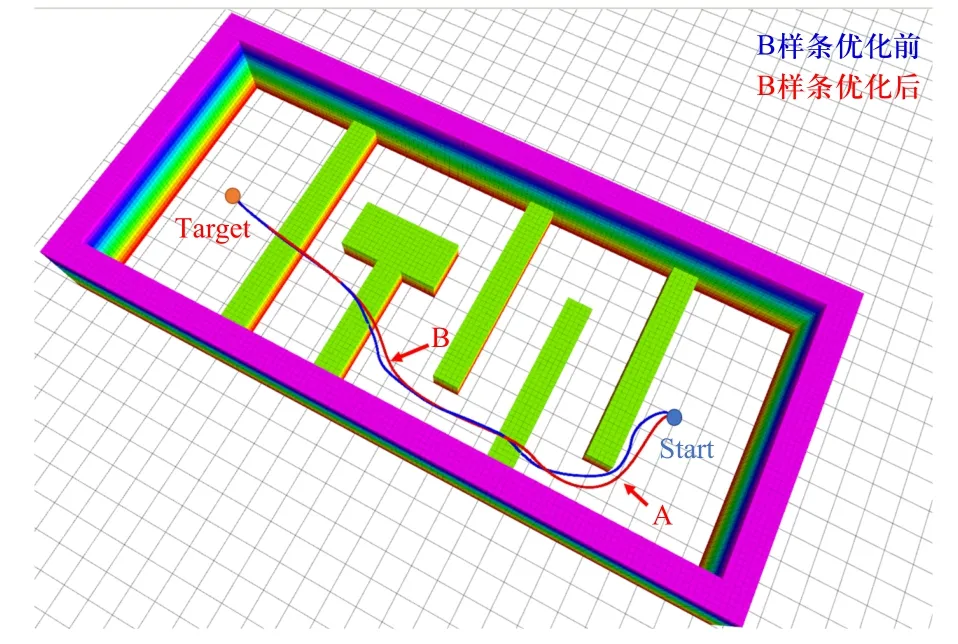
图12 B 样条优化前后轨迹对比Fig.12 Comparison of trajectories before and after B-spline optimization

B 样条优化后，轨迹离障碍物距离显著提升，轨迹平滑度显著提高.在图12 中A 所指处，紧贴拐角的路径优化后与障碍物保留一定的安全距离，在B所指处，路径优化后模态平顺切换.

轨迹优化前后后结果如表2 所示.

轨迹优化结果表明轨迹优化充分发挥了机器人空中模式下的强机动性，保留了空中相较于地面的高速度并约束了地面行驶速度，提升了障碍物距离从而保证安全性，并完成了地面模式下曲率优化的目标.

结 论

本文提出一种改进运动原语生成的Kinodynamic A*算法用于陆空两栖机器人路径规划.通过增大空中模式下的加速度输入改进运动原语生成，并在后续剪枝和轨迹优化上做相应适配，在仿真场景下验证了算法的性能.算法应用于陆空两栖机器人路径规划，仿真结果表明在飞跃障碍物需求较多的所设场景下，路径总时间平均降低6.7 s，飞行平均速度平均提升54.1%，路径总代价平均降低22.00%，算法运行时间平均降低0.069 s，算法充分发挥了陆空两栖机器人上的强机动能力与高续航能力.