巨型臂式离心机的试验不平衡量识别方法与试验

凌道盛，胡承华，邱冰静，郑建靖

（1.浙江大学 建筑工程学院岩土工程研究所，浙江，杭州 310058；2.浙江大学 超重力研究中心，浙江，杭州 310058）

由于有效负荷大、离心加速度高、离心超重力场均匀性好，臂式离心机已广泛应用于岩土工程、水利工程等传统领域[1-2]，在爆炸试验、深地深海工程等领域有应用前景[3-4].不平衡量是引起离心机振动的主要因素[5-6]，不仅影响离心模型试验精度，甚至诱发离心机结构损坏[7]或动力失稳破坏.因此，不平衡量识别成为臂式离心机设计和运行的关键.

20 世纪60 年代，GOODMAN[8]通过不同配重试验标定工作转速下不平衡量与主轴振动间的传递关系，提出了转子不平衡量识别的影响系数法.针对线性转子系统，RAFAQ 等[9]利用主轴振动与转速的相关性，提出了基于不同转速振动工频成分的不平衡量识别方法.赵嗣芳等[10]提出一种基于改进去趋势波动分析和线性判别式分析的检测方法，提升了不平衡量检测精度.ALVES 等[11]用5 阶泰勒级数展开来表示油膜力，采用数值方法来计算影响系数，并通过试验验证了其识别精度.对于过临界转速的柔性转子，模态平衡法基于主轴振动监测，通过将转子的转速提高到1、2···阶临界转速，逐阶进行平衡，直至达到工作转速.刘淑莲等[12]提出了基于主轴振动、不需要计算或识别非线性参数的不平衡量识别方法，试验证明该方法在转速高于1 阶转速时精度较好.

与传统转子不同，有效负荷在转臂端部的臂式离心机具有转动惯量变化大、工作转频宽、试验引起的不平衡量不可避免等特点，传统基于轴系振动的不平衡量识别方法应用于臂式离心机具有标定周期长、影响离心机运行安全及长期运行下稳定性难以保证等局限性.目前，中小型臂式离心机多采用直接测量不平衡力的方法.针对转臂相对主轴可移动的臂式离心机，冉光斌等[13]提出在转臂支承与隔振主体之间布置力传感器，通过不平衡力作用下转臂支承的顺臂方向移动压迫传感器实现不平衡力监测.韩国KOWACO 的臂式离心机将有效载荷和配重上的离心载荷传输到一对拉杆上，拉杆将净不平衡载荷传输到传感器实现不平衡力监测[14].对于转臂和主轴之间不可相对位移的臂式离心机，通常通过不平衡力引起的弯矩间接测量不平衡力.蒋春梅等[15]提出在转臂支承下底面对称布置4 个支座，支座内安装传感器，通过监测传感器数据判断转臂的不平衡.韩国KAIST 的臂式离心机在两个地脚螺栓处安装传感器测量模型与配重端之间的不平衡力[16].

随着离心机转速、转臂长度和容量的不断增加，转动惯量变化量、试验不平衡量、主轴轴颈越来越大.以超重力离心模拟与实验装置国家重大科技基础设施项目（CHIEF）正在建设的巨型臂式高速离心机（CHIEF 高速离心机）为例，轴颈超过1 m，离心加速度达1 500g，容量超过1 500g·t，需采用液压滑动轴承支承，支承刚度随转速和荷载的变化更加明显.高转速条件下离心机安全要求主轴与转臂不发生相对滑动，不允许在地脚螺栓等处安装传感器，以避免弱化整机刚度.为此，本文基于径向滑动轴承反力，开展试验不平衡量识别方法研究，以期为CHIEF 高速离心机和其他使用液压滑动轴承转子系统的设计和建设提供支撑.

1 臂式离心机不平衡及受力分析

如图1 所示，CHIEF 高速离心机的主要结构包括主轴、转臂、吊杯、驱动系统和液压轴承系统等，液压轴承系统包括上导、中导、下导3 个径向轴承和一个推力轴承.以中导中心位置为坐标原点建立固定于离心机的坐标系Oxyz.记ω为离心机的转速，上导刚度为ku，中导刚度为km，下导刚度为kd，推力轴承角刚度为kT，l1为上导与中导间距，l2为中导与下导间距，l为上导与下导间距，l3为中导与转臂轴线间距，则l=l1+l2.记γin为由于安装误差等导致的推力轴承法线与主轴轴线的角度差.

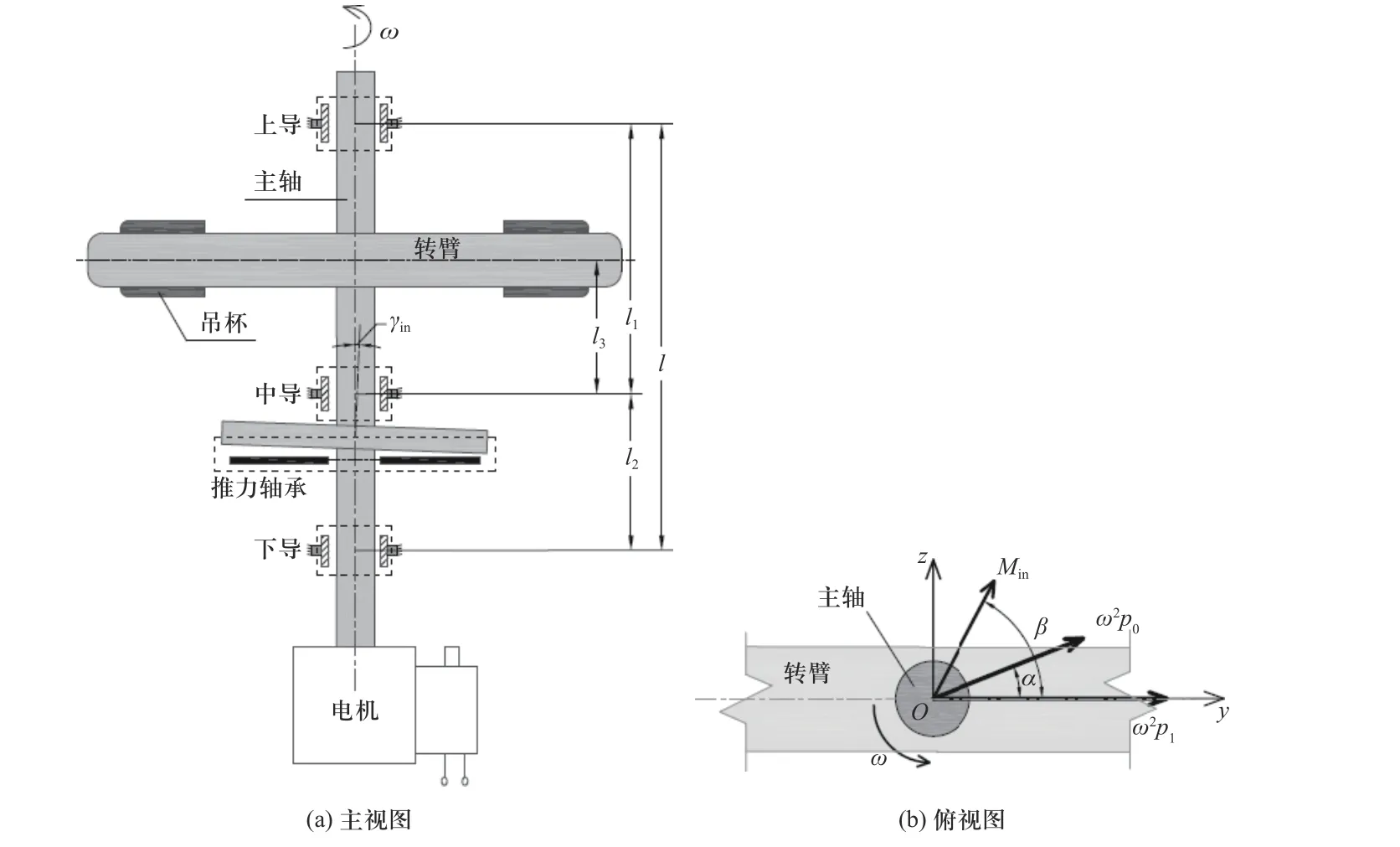
图1 CHIEF 高速离心机结构及受力示意图Fig.1 Schematic diagram of structure and force of high-speed-centrifuge built by CHIEF

为表述方便，称离心机加工及安装引起的不平衡量为固有不平衡量，记为p0=m0r0，其产生的不平衡力为ω2p0；称离心模型试验过程中配平和模型质量或质心变化引起的不平衡量为试验不平衡量p1=m1r1，其产生的不平衡力为ω2p1.不失一般性，假定p1沿坐标轴y方向.对于臂式离心机刚性转子结构，固有不平衡量和试验不平衡量主要源于转臂，可假定p0和p1位于转臂中面，距离中导l3、p0与p1之间的夹角为α.此外，记推力轴承安装误差γin引起的力矩为Min，与p1夹角在yOz平面内的投影为β.

在p0、p1和Min作用下，主轴将发生位移和变形，上导、中导和下导产生反力Ru、Rm和Rd，推力轴承产生恢复力矩Mp.对于刚性主轴，可忽略其变形，则主轴上任意一点沿y和z轴的位移可表示为y=ayx+by和z=azx+bz.图2 为主轴在xOy平面内的受力示意图.图中，Ruy、Rmy和Rdy分别为上导、中导和下导反力沿y轴方向分量，Mpz为Mp沿z轴方向的分量.在xOz平面内，同理.

图2 xOy 平面内主轴受力示意图Fig.2 Schematic diagram of main shaft stress in xOy plane

基于主轴在xOy平面内的力和力矩平衡，得

式中Ruy、Rmy、Rdy和Mpz可表示为

同理可得主轴在xOz平面内的力和力矩平衡方程.以中导为例，通过分别求解xOy平面和xOz平面的力和力矩平衡方程可得中导轴承在y轴向反力Rmy及在z轴向反力Rmz的表达式，

式中μmp和μmM为与轴承刚度有关的常数，分别表征中导关于不平衡力和推力轴承初始力矩的荷载分担比，其表达式为

式中：λu=为上导与中导的刚度比；λd=为下导与中导的刚度比；λT=为推力轴承的刚度比.同理，可获得上导和下导关于不平衡力的荷载分担比μup、μdp及其关于推力初始恢复力矩的荷载分担比μuM、μdM的表达式分别为

根据式（2）可得中导反力Rm，

式中:

2 滑动轴承刚度对荷载分担比的影响

2.1 液压滑动轴承刚度

2.1.1 径向轴承刚度

由式（3）和（4）可知，轴承刚度变化引起的刚度比变化将直接影响轴承的荷载分担比，进而影响轴承的承载分配.以CHIEF 高速离心机为例，径向轴承采用多油楔可倾瓦滑动轴承结构，上、中、下3 个径向轴承的刚度在工作转速下的数值计算结果如图3所示.由图可知，在CHIEF 高速离心机工作转速范围内，径向轴承刚度变化达数倍，且不同轴承的刚度随转速的变化规律具有差异.

图3 CHIEF 高速离心机径向轴承的刚度Fig.3 Stiffness of radial bearing of high-speed-centrifuge built by CHIEF

2.1.2 推力轴承刚度

在径向荷载作用下主轴发生倾斜，记其倾角大小为γp，可倾瓦推力轴承会产生恢复力矩Mp.当γp很小时，Mp与γp近似为线性关系[17].如图4 所示，将瓦逆时针依次编号为1、2、···n，瓦支点到坐标原点的距离记为Rz，到z轴的距离记为di.瓦的初始油膜厚度和主轴倾斜时油膜厚度（瓦未偏转的情况）分别记为h0和hi（i= 1、2、···n），则hi可表示为hi=h0-Rztan γcos[2π(i-1)/n].

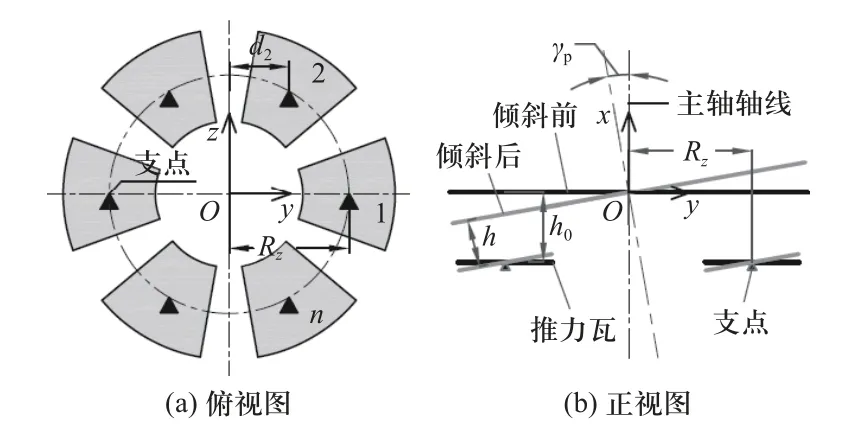
图4 可倾瓦推力轴承结构示意图Fig.4 Structural schematic diagram of tilting pad thrust bearing

推力轴承的轴向承载力随瓦块的油膜厚度变化而变化，根据恒流供油静压推力轴承的计算方法计算单个瓦的轴向承载力，初始轴向荷载为W、主轴倾角为γp时，推力轴承的恢复力矩Mp可表示为各瓦轴向承载力对z轴取矩的和，

式中：n为推力瓦数；i为推力瓦的编号.

将Rzitan γpcos [2π (i-1)/n]/h0泰勒展开并忽略高阶项，式（6）可简化为

由式（7）可知，

①Mp近似为γp的线性函数.当没有不平衡量作用时，推力轴承的初始力矩为

② 推力轴承的角刚度kT=大小与倾角无关.

对于CHIEF 高速离心机，将W= 100 t，h0= 0.2 mm，Rz= 0.645 m，n= 12 代入式（8），得CHIEF 高速离心机推力轴承的角刚度kT= 6.24×109N·m / rad.

2.2 径向液压滑动轴承荷载分担比

根据图3 所示各滑动轴承的刚度可获得轴承的刚度比随速度的变化关系，进而可利用式（3）和（4）获得径向轴承的荷载分担比.对于CHIEF 高速离心机，l= 8.660 m，l1= 4.875 m，l2= 3.785 m，l3= 2.005 m，各径向轴承的荷载分担比如图5 所示.在工作转速范围内，与相应参数的均值相比，μup的变化幅度为3.58%，μmp的变化幅度为5.61%，μdp的变化幅度为2.04%，μuM的变化幅度为0.79%，μmM的变化幅度为5.88%，μdM的变化幅度为2.20%.

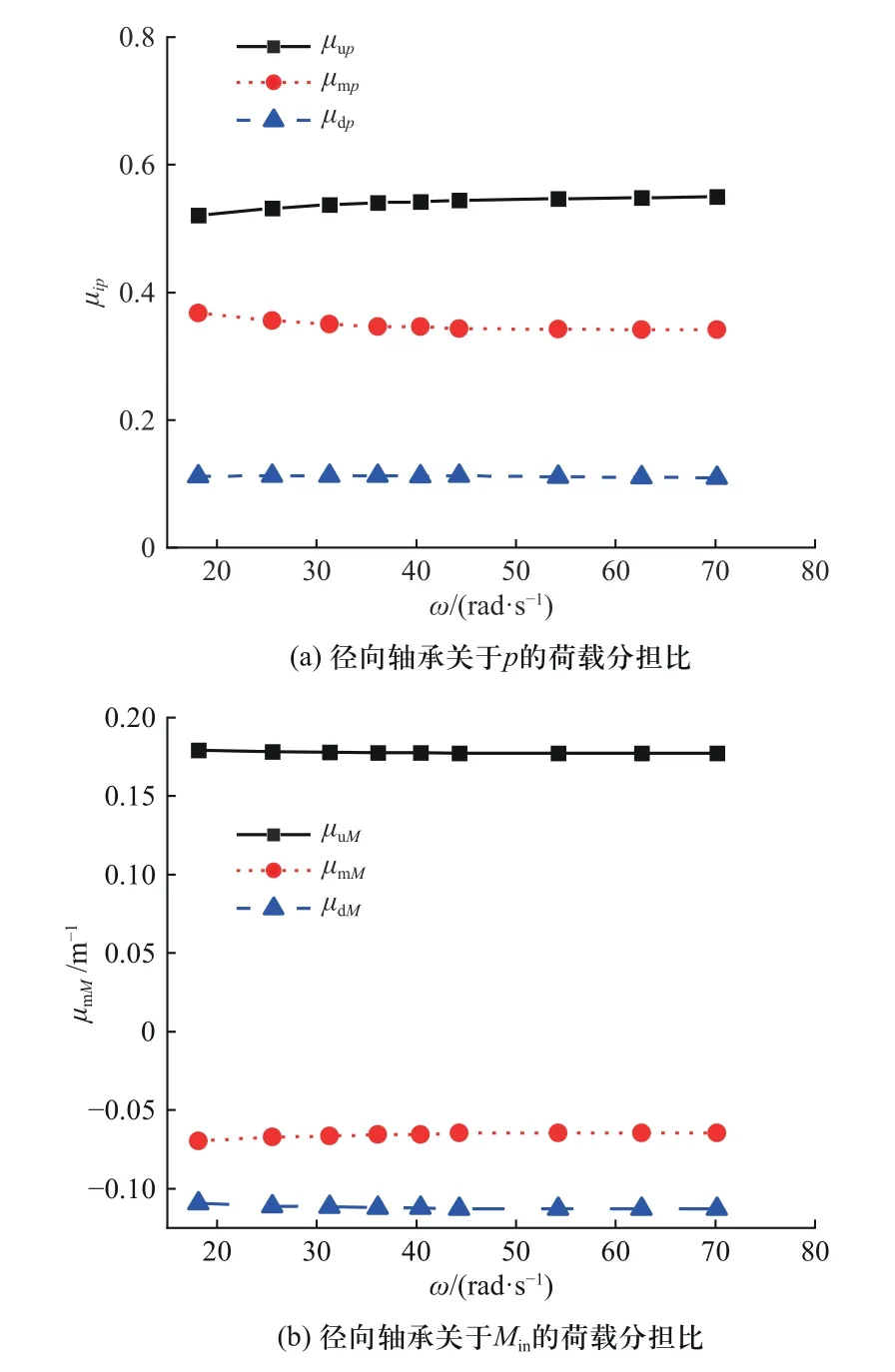
图5 CHIEF 高速离心机轴承对外荷载的荷载分担比Fig.5 Bearing ratio of reaction to load of centrifuge built by CHIEF

对比图3 和图5 可知，在工作转速范围内，各径向轴承刚度变化较大，但对轴承荷载分担比的影响不大，在轴承受力分析时可假定荷载分担比恒定.从而，理论上证明了基于径向轴承受力全工作频段识别不平衡量是可行的，比基于振动的识别方法具有更高的精度.

3 试验不平衡量识别方法与试验研究

3.1 基于径向轴承反力的试验不平衡量识别方法

上述分析表明，计算不平衡量作用下径向轴承反力时，可假定荷载分担比为固定值.由式（5）得试验不平衡量p1表示为，

式中:

考虑到加工及安装等误差因素的影响，在对不平衡力进行识别标定时，可将μmp、p0、μmMMin、α、β等列为未知参数.以中导为例，基于式（9）所示的Rm与试验不平衡量p1的方程，通过标定试验可获得方程中需标定的未知参数.在进行离心模型试验时，通过实时提取中导反力值的0 Hz 成分Fm0作为Rm值，即可实时识别臂式离心机的试验不平衡量p1.

为验证上述不平衡量识别方法的有效性，本研究基于国内某大型液压滑动轴承台架，对识别方法进行试验验证.

3.2 试验方案

试验台架结构如图6 所示，采用液压滑动轴承承载.由于实验条件限制，试验台架仅包括两个多油楔可倾瓦径向滑动轴承和一个推力轴承.为与上文表述一致，分别称该两径向轴承为中导和下导，令试验台架上导刚度ku= 0.主轴为刚性轴，为模拟臂式离心机的试验不平衡量，在推力头上部特定位置安装质量块，作为试验台架的不平衡量，质量块安装位置的回转半径为1.08 m.中导每块导瓦背侧均安装力传感器监测导瓦反力，通过矢量合成实时计算合力作为中导反力Fm.

图6 轴承试验台结构示意图Fig.6 Structure diagram of test bench

本次试验共进行4 组，每组试验安装的质量块大小不同，表1 给出试验的具体参数.所有工况下的轴瓦受力数据采集均在导瓦瓦温、油温和油膜厚度等参数稳定后进行.

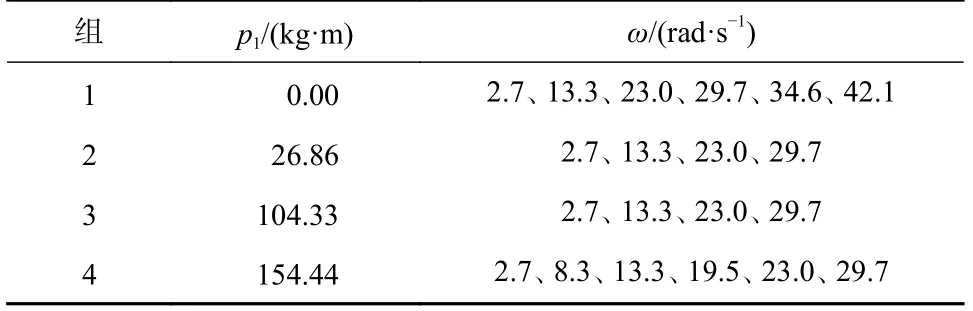
表1 试验工况Tab.1 Test conditions

3.3 试验数据分析

对于任一试验工况，通过采集数据的处理可获得试验台架中导反力值Fm的时程曲线，通过频谱分析可获得0 Hz 成分Fm0.以p1= 26.86 kg·m，ω为13.3和29.7 rad/s 时为例，如图7 所示为数据采集获得的中导反力值Fm的时程曲线，可见中导反力值存在明显的0 Hz 成分、转频成分和其他成分.图8 所示为通过频谱分析获得的0 Hz 成分Fm0随ω2的变化规律.由图可见，高转速时Fm0与ω2存在明显的线性关系，轴瓦的承载性能较稳定，而转速较低时，曲线出现“上翘”现象.导致Fm0与ω2关系曲线在低转速段“上翘”的原因包括：Fm0受到Min影响相对显著；低转速时油膜尚未完全形成，导致轴承承载性能极不稳定，μmp、μmM与高速稳定状态下存在差异.

图7 中导反力值的时程曲线：p1 = 26.86 kg·m Fig.7 Time history curve of middle radial bearing force: p1 = 26.86 kg·m

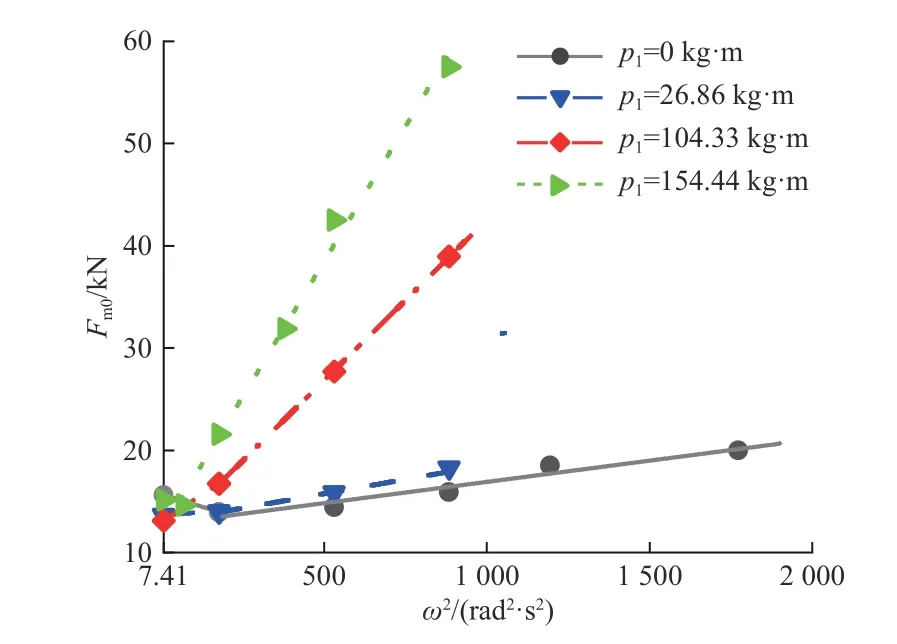
图8 实测Fm0 与ω 的关系Fig.8 Relationship between measured values of Fm0 and ω

基于式（5）对任意3 组试验数据采用最小二乘法可拟合p0、μmMMin、α、β、μmp的值，并利用剩余1 组数据对识别结果的有效性进行验证.由于采用不同组试验数据进行拟合得到的各参数较为接近，限于篇幅，本文仅给出采用1、2、4 组试验数据进行拟合的结果.通过上述拟合方法获得各参数的拟合结果为：p0= 23.38 kg·m，μmMMin= 14.11 kN，α= 3.56 rad，β=0.55 rad，μmp= 0.42，拟合结果相对误差基本都在8%以内.

为评价数据拟合结果的合理性，基于各参数的拟合结果及式（9），根据图8 中实测的Fm0反算各工况下试验不平衡量的计算值，并与实际不平衡加载量进行对比.定义试验不平衡量的识别误差为×100%，可得试验不平衡量的识别误差与试验转速的关系如图9 所示.由图9 可见：

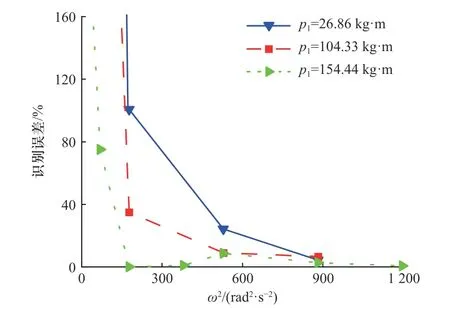
图9 试验不平衡量识别误差Fig.9 Identification error of test unbalance

①转速越高，识别误差越小，高转速时识别误差小于9%.一方面是因为识别方程的形式决定了当ω较小时，Fm0微小的误差都会对p1产生很大影响；另一方面是因为低转速时油膜尚未稳定，轴承受力不稳.CHIEF 高速离心机的工作转速下限为18.1 rad/s，可与现有识别法联合使用，满足实际需求.

②试验不平衡质量越大，识别误差越小，这也与识别方程的形式有关.

③基于识别参数获得p1= 104.33 kg·m 时的Fm0-ω2曲线与其他试验不平衡量对应曲线规律相同，这说明基于径向导轴承反力监测的数据拟合方法适用于试验不平衡量识别，验证了识别方法的有效性.

需要说明的是，在拟合计算时，因反三角函数解的不唯一导致α和β有两解，而其他参数相同，但这不会对试验不平衡量的识别结果产生影响.

4 结 论

针对超大型臂式离心机不平衡量的识别问题，本文提出了一种基于径向滑动轴承反力的试验不平衡量识别方法，并通过台架试验进行了初步验证，得到以下结论.

①理论推导表明，在不平衡力作用下，轴承的荷载分担比受转速影响较小，基于径向轴承反力的试验不平衡量识别方法能够较好地识别巨型臂式离心机的试验不平衡量.

②试验结果表明，所提出的识别方法对离心机较高工作转速时的不同不平衡量具有良好的适用性，可应用于在建巨型臂式高速离心机.