引信系统螺纹连接界面的冲击传递特性模拟方法研究

苏煜，李毅，刘小玉，周春燕

（1.北京理工大学 宇航学院，北京 100081；2.中国工程物理研究院电子工程研究所，四川, 绵阳 621900）

螺纹连接的可靠性、工艺制作的简易性、安装与拆卸的便捷性，使螺纹连接结构广泛用于侵彻弹的引信连接.引信系统控制着弹药是否起爆，起爆点的位置对作战效能起着至关重要的作用，引信系统内部电子元器件的安全性、信号识别的准确性一直都是引信研制的重要问题[1-2].螺纹之间的连接结构复杂、接触面不连续、在冲击过程中多次碰撞[3-4]，导致大量的非线性因素，冲击过载的传递在螺纹连接结构中难以预测，而引信的力学环境关系到电子元器件的安全性，过载的信号识别决定了引爆火药的时机，因此研究螺纹连接界面的冲击过载传递特性非常重要.

针对螺纹连接在冲击载荷作用下的力学行为，很多学者对螺栓连接进行了研究.GRIMSMO 等[5]通过实验研究了钢螺栓端板连接处在冲击荷载作用下的行为，发现相比于准静态试验，螺栓的变形更加对称，连接处吸收的能量也更多.NGUYEN 等[6]研究了霍普金森拉杆系统中螺栓紧固件的螺纹形状对应力波传递特性的影响.YU 等[7]通过实验与有限元的方法，研究了循环载荷作用下螺栓连接结构的应力分布、应变累积以及磨损机制.LIU 等[8]进行了有限跨度螺栓连接复合防护结构的弹道试验，研究了螺栓连接区域的承载和破坏特性，以及结构各部分的能量耗散.GUO 等[9]将装配的螺栓法兰接头连接在霍普金森入射杆的底端，研究了螺栓法兰接头在不同载荷脉冲作用下的振动和耗散响应.SANBORN 等[10]通过冲击和准静态两阶段加载研究了摩擦对螺栓连接临界滑移的影响.ZHENG 等[11]建立含无限元的三维有限元数值模拟模型，研究了单激波作用下螺栓接触状态的演变和松动过程.上述对螺栓连接结构的研究，冲击载荷主要通过连接结构的结合面进行传递，螺栓与螺帽的螺纹连接界面对冲击载荷传递的影响占比较小.

在侵彻弹中引信的冲击载荷主要通过螺纹连接界面进行传递，目前对于整个弹体的试验研究，发现由螺纹旋入的引信体，除了受到弹体过载外，还会承受额外的冲击，引信承受比弹体更大的过载[12-15].ZHANG 等[16]采用有限元仿真模拟了侵彻弹打击目标的过程，阐明了在侵彻过程中弹体与引信之间的螺纹变形会产生间隙，并由于间隙的存在，螺纹连接面上将发生相互碰撞，螺纹的碰撞对引信内部的过载有非常严重的影响.张冬梅等[17]对侵彻过程的测试信号进行时频分析，发现测量信号中存在与螺纹连接结构的振动频率一致的振动信号，该频率成分的信号幅值较高对过载产生较大影响.以上对于整弹的研究，由于弹体本身结构以及被冲击靶体的结构动力学特性会导致传递到螺纹的冲击信号非常复杂，不利于开展螺纹连接界面的冲击过载传递特性分析，因此需要设计简洁的冲击实验，对单独的螺纹连接结构件输入单激波脉冲信号来准确获取螺纹连接界面的冲击传递特性.

此外，螺纹连接结构复杂、接触较多，存在大量非线性因素.目前针对螺纹结构的研究主要采用实验和有限元数值分析的方法，而在有限元数值分析过程中，螺纹结构三维模型建模困难，需要的网格较多，将花费大量的计算资源.同时在大型武器中存在较多的螺纹结构，由于计算资源的限制，有限元方法无法实现考虑每个螺纹结构精细模型的分析计算，因此需要螺纹结构的简化模型代替，已有部分学者对螺纹结构的简化模型进行了研究.贺李平等[18]实体螺栓联接模型和梁单元联接模型在模态和应力分析中具有广泛的适用性； ZHAO 等[19]用薄层单元表示螺栓连接结构之间的接触刚度，得到螺栓界面接触刚度随螺栓预紧力变化的定量规律；ADEL 等[20]提出双层薄层单元模拟混合结构中的螺栓接头界面并与模态试验验证，表明双层薄层单元模型可用于大型结构中螺栓接头界面的模态分析；鄢阿敏等[21-22]用薄层单元模拟侵彻弹中弹体与引信系统的螺纹连接，有效提高了仿真模型模态分析的仿真精度.以上针对薄层单元模拟螺纹连接结构动态响应的研究主要集中在结构的振动分析，而适用于振动分析的薄层单元应用于冲击时仿真结果不理想，未考虑冲击过程中螺纹的碰撞作用对结构力学环境的影响，螺纹结构在冲击工况下的简化模拟需要进一步的改进.

为了使螺纹结构件的撞击面受到均匀的应力脉冲，本文采用大直径霍普金森压杆系统，对螺纹结构件进行冲击.建立有限元精细螺纹结构件开展冲击数值模拟，由实验测量数据验证有限元模型的有效性，对比了螺纹结构件中心位置与结构件顶端的加速度峰值大小；并通过有限元分析了预紧力对螺纹结构件的冲击响应影响规律.最后提出考虑螺纹间碰撞作用的非线性薄层单元简化模型，并利用简化模型分析了不同层数螺纹对冲击响应的影响.

1 大直径霍普金森杆冲击实验

在霍普金森压杆系统的冲击过程中，子弹撞击入射杆产生的应力波，从0 到达峰值的上升速度快，能产生非常大的加速度，满足引信系统在受到冲击过载时的高g值要求.同时本文研究的螺纹结构直径较大，常用的霍普金森杆件直径较小，冲击面积较小，容易产生局部应力集中，不能对结构件造成均匀的应力冲击，冲击效果较差.因此针对本文研究的螺纹结构件，需使用大直径的霍普金森压杆系统对螺纹连接结构件进行冲击实验.

1.1 实验装置

霍普金森杆压杆系统由圆柱形的子弹、入射杆、透射杆组成.子弹长600 mm、入射杆长4 000 mm、透射杆长3 000 mm，直径均为100 mm，如图1 所示.

图1 霍普金森压杆系统Fig.1 Impact test of the Hopkinson pressure bar system

螺纹连接结构试件由带有外螺纹的内芯以及带有内螺纹的套筒组成，套筒长140 mm、直径140 mm，内芯长100 mm、直径100 mm，螺纹规格为ISO 标准的M10×100 mm，啮合长度为100 mm，如图2 所示.

图2 螺纹结构件Fig.2 Threaded structure

为了获得冲击载荷作用下螺纹连接结构件加速度响应，在套筒与内芯的凹槽内粘上b-k 加速度计，如图3 所示；为了获得冲击波的信号，在入射杆200 mm 处贴上应变片.

图3 套筒与内芯加速度计的位置Fig.3 Positions of sleeve and accelerometer

使用高速摄像仪拍摄子弹的飞行过程，根据位移与时间的关系计算出子弹的撞击速度为4 111 mm/s，如图4 所示.

图4 测量子弹的撞击速度Fig.4 Measuring the impact velocity of the bullet

2 螺纹结构精细建模与计算

有限元仿真可以通过数值计算获得实验中难以测量的结构内部数据，同时相较于实验更容易观察螺纹结构件的整个冲击变化过程，通过有限元仿真的方法可以更加全面、有效地研究螺纹连接界面的冲击传递特性.因此，建立具备螺纹细节特征的精细有限元模型，计算分析螺纹结构件在大直径霍普金森杆冲击下的力学行为.

2.1 有限元精细建模

本文采用八节点六面体网格按照实验设备等比例建模.在相同网格密度下六面体网格数量是四面体网格的1/4，且四面体网格容易出现剪切自锁，使结构刚度过大，六面体网格很大程度上缩减了计算所需的时间成本，仿真结果有更高的精确性.

螺纹牙型是螺纹连接结构件的关键部位，螺纹牙型处的网格密度对模型的仿真精确性影响较大，因此需采用较密的网格对螺纹进行划分.本文对M10 螺纹中经处布置6 层网格，在牙尖处布置2 层网格，1 层螺距布置16 层网格，网格的特征尺寸为0.4 mm.由于螺纹的导程角对螺纹结构的刚度有影响，也会在冲击过程中影响螺纹之间的不均匀接触状态，不能简单地将螺纹连接结构当作轴对称结构进行建模计算，因此本文对螺纹连接结构的精细建模考虑了螺纹的导程角，螺纹的导程角将使螺纹连接结构建模难度大大增加，需要对单层螺纹进行精细的切割设计，才能实现螺纹处六面体网格的螺旋上升.同时为了使内外螺纹牙型之间啮合效果较好，建模时使内芯上的内外螺纹与套筒上的外内螺纹无缝啮合.子弹、杆件与垫片几何模型为圆柱形，无复杂的细节特征，可以使用较大尺寸的网格进行划分，采用的网格特征尺寸为7 mm.螺纹连接结构件共637 444 个单元，788 758 个节点；子弹、杆件、垫片共117 392 个单元，129 444 个节点，有限元模型如图5所示.

图5 霍普金森杆冲击螺纹结构件的有限元模型Fig.5 Finite element model of Hopkinson rod impact threaded structure

2.2 前处理设置

对网格模型进行前处理设置，定义子弹与入射杆、入射杆与垫片、套筒与垫片、内螺纹与外螺纹、垫片与透射杆面对面自动接触，设置静摩擦因数为0.2，动摩擦因数为0.15，将刚度大的材料设为主从面、反之则为副从面.由于螺纹处的网格较密，采用共节点建模方法将产生大量网格，将浪费大量的计算资源，因此对套筒顶盖、内芯内部与螺纹牙型不共节点建模，采用tie 接触的方式连接本是完整体的套筒以及内芯，定义套筒顶盖与套筒内螺纹、内螺纹与内芯tie 接触.

将实验得到的子弹速度4 111 mm/s，以设置初始速度方式施加到组成子弹的每一个网格节点上.此方法相较于在入射杆端面直接加载应力波，仿真还原性更高，螺纹结构件的加速度峰值响应精度更好.本文中所有模型皆采用该冲击工况.

分别对不同组件设置材料属性，各组件均采用弹塑性模型，子弹、杆件的材料为铝，螺纹结构件的套筒为钛合金TC11，内芯为05Cr17Ni4Cu4Nb.材料参数如表1 所示.

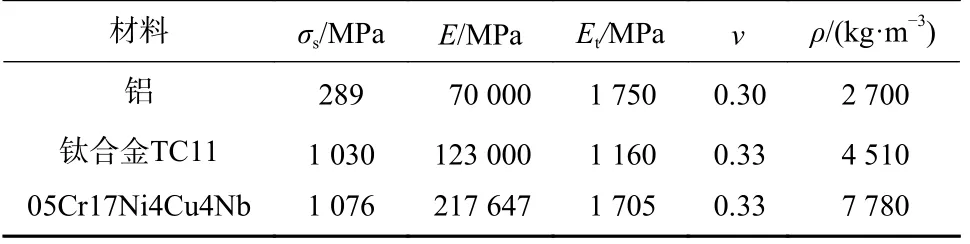
表1 材料参数Tab.1 Material parameters

2.3 有效性验证

将实验测得入射冲量以及螺纹结构件加速度数据与有限元模型对应位置处的计算结果对比，验证仿真模型的有效性.

如图6 所示，子弹撞击入射杆产生的入射冲量，实验与数值结果一致性较好，表明数值模拟作用于结构件的入射冲量与实验基本一致.入射冲量是由入射应力与杆件轴向截面面积相乘，再进行关于时间的积分计算得到.

图6 实验与仿真的入射冲量Fig.6 Incident impulse of experiment and simulation

由实验和数值得到的套筒顶端加速度响应如图7 所示，内芯底端的加速度响应如图8 所示.从图中可以看出，套筒与内芯的实验与数值加速度响应，整体趋势一致性较好，加速度峰值相差较小，表明了螺纹结构件有限元精细模型的有效性.

图7 实验与数值的套筒加速度Fig.7 Experimental and numerical sleeve acceleration

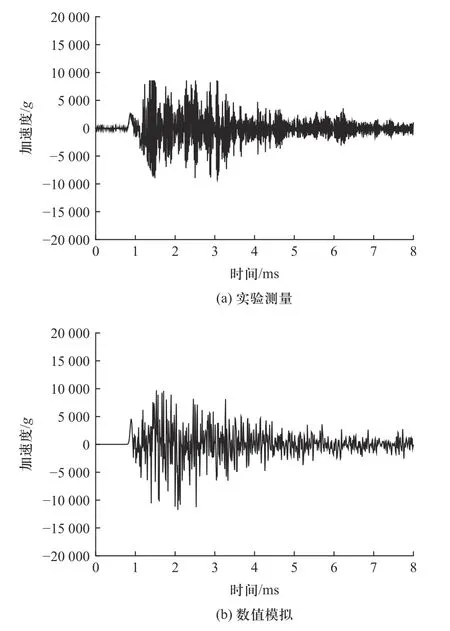
图8 实验与数值的内芯加速度Fig.8 Experimental and numerical core acceleration

2.4 内芯的冲击过载响应

引信系统通过对加速度信号的识别来控制火药的引爆时机，研究螺纹连接结构的内芯冲击过载响应特性是引信控制设计的重要问题依据之一.

通过螺纹结构件精细模型的数值计算，选取内芯距离端面50 mm 处的中心节点与套筒顶端处的加速度响应，如图9 所示，从图中可以看出，内芯中心节点的加速度响应峰值比套筒顶端更大，表明螺纹的相互碰撞将加剧过载的传递，内芯的力学环境更为恶劣.同时还对加速度响应曲线计算了FFT 谱，如图10所示，其中大部分能量集中在6 600 Hz 的基频上，内芯中心各频率的振幅明显比套筒顶端的要强，更为明显地表现出冲击载荷引起的螺纹相互碰撞，将产生更为剧烈的动态响应.

图9 内芯与套筒的加速度峰值对比Fig.9 Comparison of internal and external acceleration peaks

图10 加速度响应FFT 谱Fig.10 Acceleration response FFT spectrum

因此，引信系统中螺纹连接的内部电子器件将受到更强的过载冲击，需要更为谨慎地考虑内部电子器件的安全，以及设置更准确的起爆阈值，达到最大的爆炸效果.

2.5 预紧力对冲击过载的影响

在矩形应力波冲击载荷作用下螺纹连接的松动与初始预紧力有关[11]，由此可见螺纹连接结构预紧力的存在，会对螺纹连接结构在冲击载荷作用下的力学行为产生影响.因此针对预紧力对内芯的冲击过载影响进行分析，在内芯的底层网格的中面创建预紧力横截面，并分别施加30、50 MPa 的截面预紧力.其中施加30 MPa 截面预紧力的内芯应力分布如图11 所示，在预紧力作用下前4 层的螺纹牙型主要承受了阻止内芯进一步旋入的压缩应力，螺纹凹槽受到防止滑移的拉伸应力.

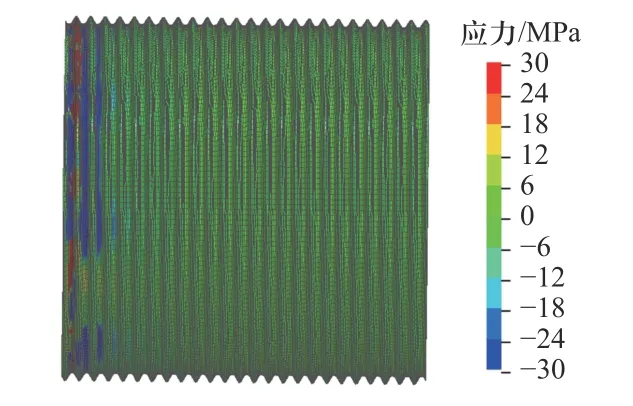
图11 内芯的应力云图Fig.11 Stress cloud picture of inner core

提取不同预紧力模型内芯中心节点加速度响应，并进行FFT 变换，进行频谱分析，为了便于比较，频率范围设定在20 kHz 以内，如图12 所示.由图中可以看出，预紧力的存在一定程度上抑制了内芯的动态响应，施加的预紧力越大，抑制效果越明显.观察6 600 Hz 的基频响应处，可以明显看到，在施加50 MPa 预紧力的工况下，内芯的基频响应获得了较大程度的抑制，说明施加一定载荷的预紧力可以有效减少内芯加速度峰值的响应，有助于缓解引信内部电子器件的安全问题.

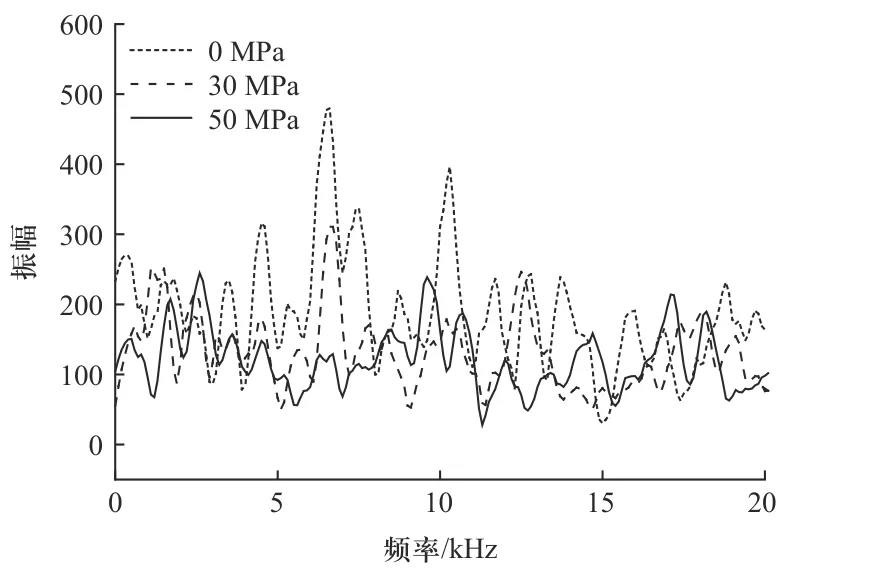
图12 不同预紧力的内芯加速度响应FFT 谱Fig.12 FFT spectrum to different preloading forces

提取30 MPa 预紧力作用下，内芯底部单元的应力动态响应，如图13 所示，从图中0～2 ms 的应力响应可以看出，结构的动态响应呈现上升趋势.是由于冲击应力波在结构内往复传播的过程中，压缩应力波传播到端面反射为拉伸应力波，拉伸应力波导致螺纹牙型分离，分离后的螺纹牙型再次发生碰撞，产生新的应力波，应力波的叠加导致在一段时间内，结构的动态响应加剧.观察0 ms 时的初始预紧应力和10 ms 时的预紧应力，发现在冲击载荷作用后结构内部的预紧力减弱.是由于反射后的拉伸应力波导致螺纹牙型啮合松动，应力波在结构内的反复传播过程中，多次反射的拉伸应力波作用下，导致整体螺纹结构件松动，预紧力减小.

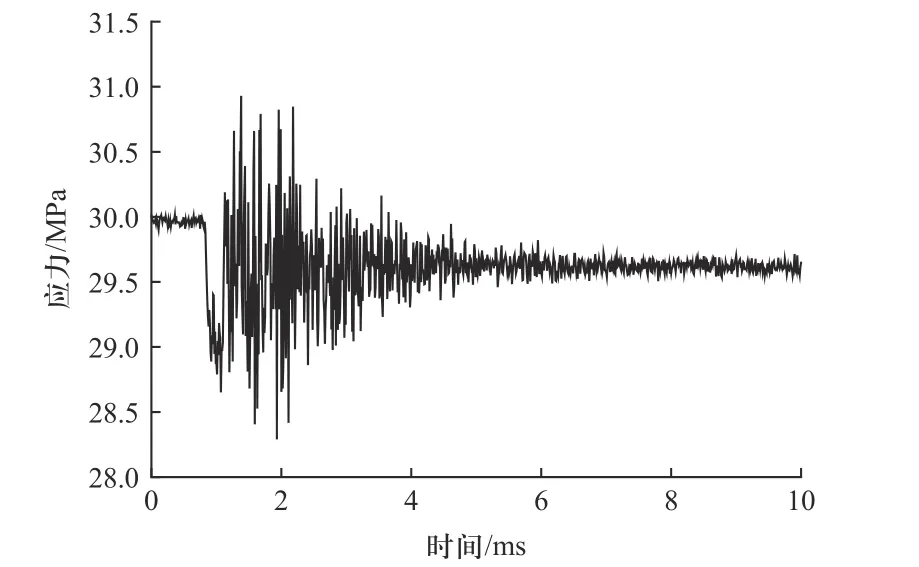
图13 内芯底部单元的应力响应Fig.13 Stress response of inner core bottom element

3 螺纹结构非线性薄层单元简化模型

螺纹连接结构复杂，精细有限元建模难度大，武器中螺纹结构较多，无法实现每个螺纹的精细建模计算.需要有较高可行性的简化模型实现建模的简单化，避免复杂模型建模过程中因忽略螺纹结构造成的计算精度下降.

目前有很多学者采用各向同性薄层单元模拟简化螺纹连接结构，简化模型的研究主要集中在结构的模态分析与频率分析上，能很好地在模态与频率分析上替代复杂的螺纹连接.但是对于冲击过载问题的研究较少，所提出的薄层单元简化模型对冲击过程中螺纹结构的加速度响应精度较差，无法有效表征冲击过程中的碰撞作用.

因此本文提出一种考虑螺纹间碰撞过程，并具有更高加速度峰值响应精度的非线性薄层单元简化模型.

3.1 非线性薄层单元

在冲击工况下，螺纹牙型的碰撞作用是影响结构力学响应的重要因素，因此提出一种考虑螺纹碰撞作用的非线性薄层单元简化模型来模拟螺纹连接在冲击工况下的力学行为.

针对螺纹连接结构在受到冲击压缩作用时的螺纹牙型的力学行为进行分析.初始状态下套筒外内螺纹受到冲击载荷的作用向上移动与内外螺纹进行碰撞发生压缩变形，导致螺纹牙型之间产生间隙；随后内外螺纹脱离接触发生分离，在微小的间隙中运动一段时间后又在螺纹牙型的另一侧碰撞再分离，如此周而复始.螺纹牙型之间的碰撞分离过程，如图14 所示.通过各向同性的薄层单元模拟螺纹连接并借鉴动刚度的方法，将薄层单元一段微小剪切变形的刚度设置为0，应力状态为0，以此来表征螺纹牙型碰撞分离过程中的无约束自由状态.薄层单元的微小变形如图15 所示.

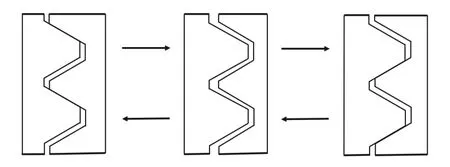
图14 螺纹牙型碰撞分离过程Fig.14 Collision separation process of thread profile

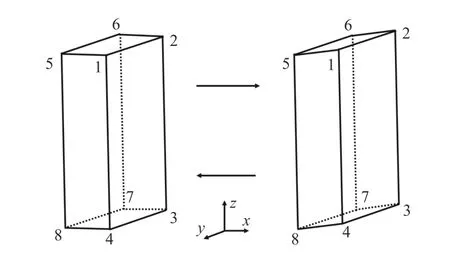
图15 薄层单元的微小剪切应变Fig.15 Tiny shear strain of thin layer element

在有限元的显示分析中，薄层单元应力更新的本构方程表示为

在薄层单元沿轴向的剪切变形γ ＜0 或γ0＜γ时，刚度矩阵

在薄层单元长度方向的剪切变形0 ＜γ ＜γ0时，Kij=0，并且应力的更新方程表示为

从上述对非线性薄层单元如何表征在冲击工况下螺纹连接的碰撞作用的描述，要实现螺纹连接结构模型的简化，需要确定非线性薄层单元的4 个参数：密度 ρ、泊松比 υ、弹性模量E或剪切模量G、沿轴向的微小变形 γ0.其中E和G可通过各向同性材料的公式相互转换.

3.2 参数的确定

由于薄层单元模拟的是相互啮合的螺纹牙型，内外螺纹牙型的体积分数各占1/2，因此密度和泊松比，采用内外螺纹构材料参数的均值.

剪切模量可由鄢阿敏等[22]提出的理论计算公式获得，表达式为

式中：t为薄层单元的厚度；A为薄层单元与被连接结构的接触面积；K为螺纹连接结构的刚度.K可以通过有限元模拟一层啮合螺纹牙型的静力学拉伸行为获得，也可采用ZHANG 等[16]提出的螺纹连接结构刚度的理论计算方式，具体的表达式为

式中：Eb和En分别为内芯和套筒的弹性模量；Sb和Sn分别为内芯和套筒的横截面积； δba、 δna分别为内芯和套筒的螺纹牙在单位力作用下的轴向总挠动.其中下标b 和n 分别表示内芯和套筒；a 表示螺纹牙在单位力作用下产生的所有轴向挠度之和（弯矩引起的挠度、剪切载荷引起的挠度、螺纹牙根部倾斜引起的挠度、螺纹牙根部剪切引起的挠度、以及螺栓和螺母径向收缩和膨胀引起的挠度）.

针对薄层单元轴向微小变形 γ0，由单元角应变的计算公式得到：

式中 Δ为螺纹牙型的碰撞间隙，由于难以计算螺纹牙型碰撞变形产生的间隙，将冲击波的峰值应力以分布载荷的形式作用于一端固定的长方形单元上，产生的压缩位移视为由碰撞变形产生的间隙.因此间隙的计算公式为

式中：σmax为冲击波峰值应力；l为薄层单元长度.

3.3 简化模型的建模

螺纹连接结构件的简化模型由3 个部分组成：内芯、薄层单元、套筒.其中薄层单元的厚度2 mm与螺纹牙型的尺齿高相同，分别向内芯与套筒延伸1/2 的厚度，长度8 mm 为2 倍螺纹的层高，一个薄层单元表征两层螺纹牙型的相互啮合状态；由于薄层单元替代螺纹牙型向内、向外延伸了1 mm，因此内芯外径收缩为98 mm，套筒内径扩大为102 mm，其他特征尺寸保持与实验一致；有限元简化模型如图16所示.

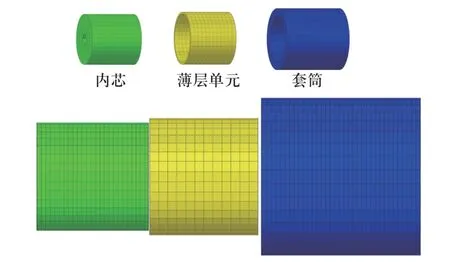
图16 螺纹结构件简化模型Fig.16 Simplified model of threaded structure

内芯、套筒、薄层单元均采用六面体网格划分，薄层单元表面与内芯、套筒共节点连接，简化模型共11 076 个单元，13 241 个节点，六面体网格的最小特征尺寸为2 mm.相比于螺纹结构件的精细模型，网格数量减少为精细模型的1/48，最小特征尺寸增大5 倍.在显示动力学分析中，材料的波速与网格最小特征尺寸决定了计算过程中的最小时间步，网格的数量决定了计算的次数.因此简化模型将比精细模型的计算效率提高了240 倍，同时释放了计算机的内存空间，解决了螺纹连接结构计算时间过长、占用内存过多，以及无法对拥有较多螺纹连接结构的大型武器建模计算等问题.

对非线性的薄层单元的本构方程，按照式(1)和式(3)进行UMAT 子程序的编写.设置调用自定义本构方程的材料卡片，编辑对应的材料参数，赋予非线性薄层单元的材料属性.薄层单元的参数如表2 所示.其他前处理设置与精细模型保持一致.

表2 薄层单元材料参数Tab.2 Thin-layer element material parameters

3.4 简化模型的有效性分析

由于螺纹连接的引信结构内部力学环境的研究是引信结构设计的关键，需要最大程度上确保内芯的冲击响应精确度.因此将精细模型、非线性薄层单元、各向同性薄层单元内芯中心节点处的加速度响应进行对比，验证模型过载响应的有效性，如图17 所示.从图中可以看出，考虑碰撞作用的非线性薄层单元加速度响应峰值与精细模型较为接近，相较于未考虑碰撞的薄层单元有较大改进；同时薄层单元的加速度响应也表现出和加速度响应整体一致的衰减趋势，很好地表现出了螺纹连接结构给结构带来的阻尼作用.

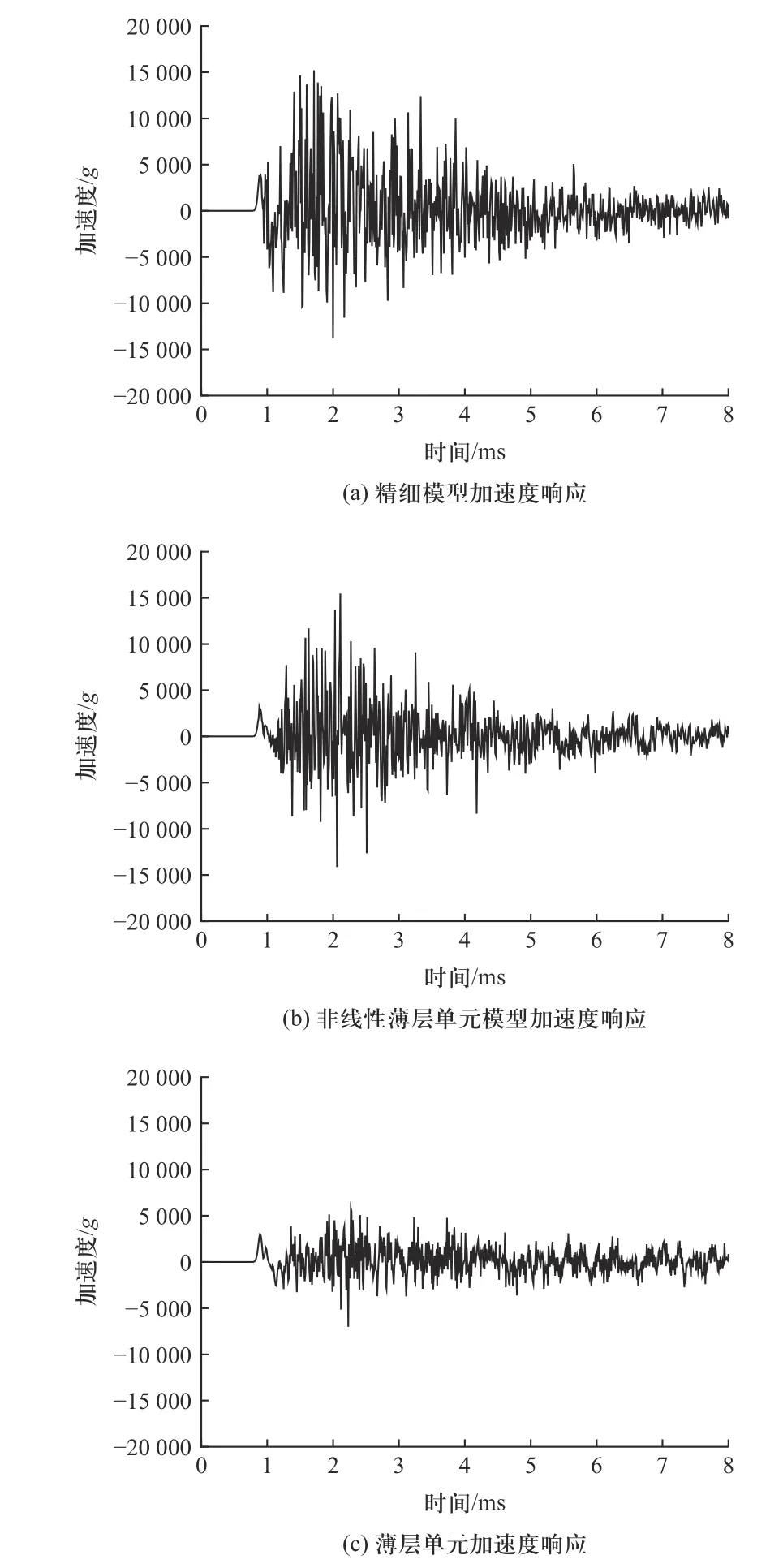
图17 3 种模型的内芯中心节点加速度响应Fig.17 Acceleration of central node of three models

将3 种模型的加速度响应进行傅里叶变换，得到FFT 谱，如图18 所示，从图中可以看出，非线性薄层单元简化模型相比于未考虑碰撞的薄层单元，在低于20 kHz 的频率部分产生的能量更大，与精细模型更为接近.非线性薄层单元整体能量有从低频到高频向下过渡的趋势，展现出薄层单元不具备的响应特性，较为贴合螺纹结构在实际冲击过程中的真实情况.在40 kHz 的高频部分显示出较高程度的一致性.

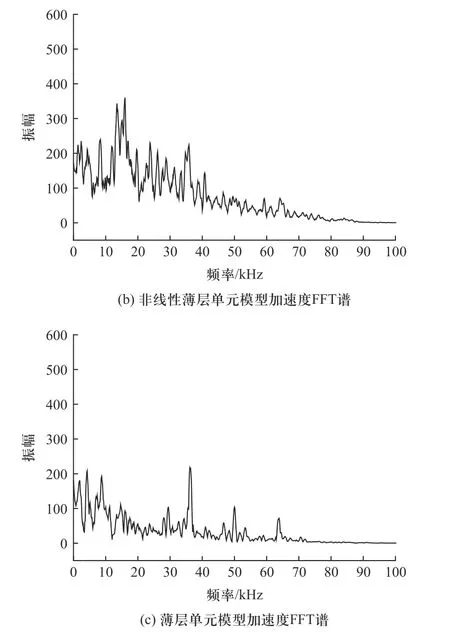
图18 3 种模型的加速度FFT 谱Fig.18 Acceleration FFT spectra of three models

结合加速度响应曲线和FFT 谱，可以得到，非线性薄层单元较好地表征了螺纹连接结构在冲击过程中的碰撞作用，相较于未考虑碰撞的薄层单元，螺纹结构的过载响应峰值精度更好，结构响应的整体趋势更为一致.本文提出的非线性薄层单元可以较好地模拟冲击工况下，螺纹碰撞导致的动态响应.

3.5 螺纹层数对冲击响应的影响

根据本文提出的非线性薄层单元简化模型，对螺纹层数进行优化设计，研究不同层数螺纹对内芯中心加速度响应的影响.简单删减薄层单元轴向的层数，以此来表征不同层数的螺纹模型，如图19 所示，黄色六面体网格为非线性薄层单元，1 层薄层单元表征2 层螺纹.其中分别为24 层螺纹的全螺纹模型，18 层螺纹的3/4 层螺纹模型，12 层螺纹的半螺纹模型，6 层螺纹的1/4 层螺纹模型.

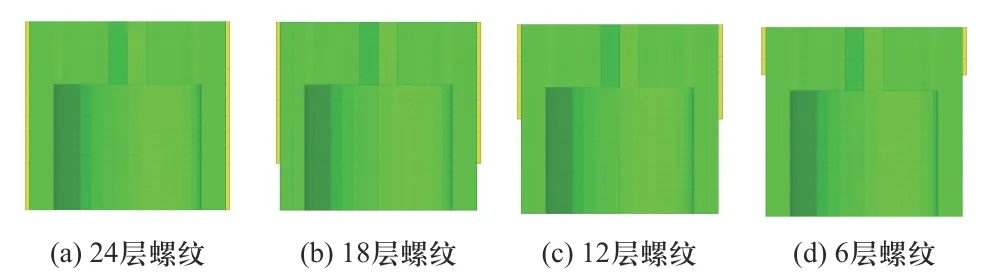
图19 不同螺纹层的简化模型Fig.19 Simplified model of different thread layers

分别选取内芯中心节点的加速度响应，并对每个加速度响应曲线进行10 kHz 的低通滤波，以便于进行不同螺纹层数加速度响应峰值的比较，如图20所示.从图中可以看出，在接近2 ms 位置处不同螺纹层模型的内芯加速度响应达到峰值，半螺纹模型的峰值响应最低，半螺纹结构相较于其他螺纹层结构表现出更好的安全性.

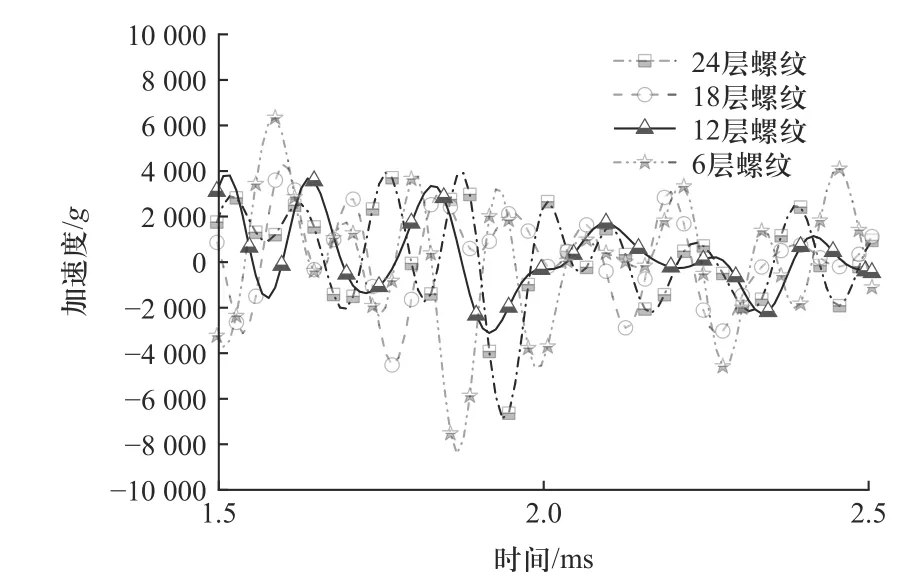
图20 不同螺纹层模型的加速度响应Fig.20 Acceleration response of different threaded models

4 结 论

通过数值模拟分析了螺纹结构件在大直径霍普金森杆单脉冲下的冲击过载传递特性，利用精细模型研究了预紧力对动态响应的影响，由实验验证了有限元精细模型的有效性.并提出了考虑螺纹间碰撞作用的非线性薄层单元简化模型，根据简化模型对螺纹层数进行了结构优化.得出以下主要结论：

①螺纹连接界面的相互碰撞将增大内部结构的过载，导致螺纹连接的内部空间力学环境更为恶劣.引信系统结构设计时需合理考虑螺纹产生的影响.

②预紧力可以有效缓解螺纹连接界面对过载的增大效果，施加一定载荷的预紧力，有助于缓解引信内部电子器件的安全问题.冲击应力波在螺纹结构件内的往复传播产生的拉伸应力波将导致螺纹结构件松动.半螺纹相较于其他层数的螺纹对过载的传递影响更小，安全性更好.

③考虑螺纹间碰撞作用的非线性薄层单元简化模型，能较好地表征冲击工况下螺纹连接界面的碰撞，相比于未考虑碰撞的薄层单元简化模型，加速度峰值响应的精确度有更好的提升.