火星超低雷诺数下螺旋桨气动性能研究

张旺旺，徐彬，张海涛，樊伟，赵之然

（1.北京理工大学 机械与车辆学院，北京 100083；2.北京理工大学 重庆创新中心，重庆 401120）

近年来，随着地球气候越来越恶劣，人们开始将目光投向太空，期望能找到一个与地球大气环境相似，可供人类居住的星球.火星上的各项物理特征与地球极为相似，都具有大气和四季更替，同时火星上曾经还存在液态水，种种迹象表明，火星上可能存在生命体[1]，这更加激发了人类探索火星的兴趣.对火星的探索有助于我们了解生命起源的意义，同时也期望能将火星开发为未来适宜人类居住的第二星球.以前对于火星的探索，主要依靠火星车和轨道飞行器[2]两种方式，这两种方式都有各自的局限性，火星车探索速度慢，范围小，受地形限制大，轨道飞行器探索范围广，但由于距离火星地表太高，只能进行宏观探索，而火星旋翼机则能弥补两者的缺点，不仅具有较高的探测速度，同时探索范围较广，不受地形的影响，还具备较高的成像分辨率.目前，国内外已经有一些机构开展了火星表面无人机的可行性研究[3].2021 年4 月19 日，随着美国NACA 团队研制的“MH”号火星无人机在火星成功试飞，标志着对火星的探索进入到无人机探索时代[4].

尽管火星上也有大气存在，但火星大气密度仅为地球大气密度1/80，并且95%是CO2，同时火星上的声速也比地球声速小很多，约为地球声速的67%，这些特征导致了火星无人机旋翼系统处于超低雷诺数、高马赫数状态.目前对火星超低雷诺数范围的气动特性研究仍较少.SUNADA 等[5]通过对20 多种不同翼型的参数进行对比分析，比较了翼型的弧度、最大弧度位置、厚度、前缘尖锐度、粗糙度等参数对翼型气动特性的影响，得出的结论是尖锐的前缘，5%的弧度，适当的粗糙度以及较薄的厚度能显著提高翼型在低雷诺数环境下的升阻特性；GROSS 等[6]应用DNS 方法对低雷诺数下翼型表面流动分离状态展开了深入研究，表明层流分离涡的形态受攻角的影响较大，随着攻角的增加，翼型表面出现层流分离、分离点前移、分离再附着以及分离泡破裂等一系列复杂现象；白鹏等[7]和刘强等[8]采用非定常层流数值模拟计算结合实验验证的方式，研究了不同迎角及不同雷诺数下翼型层流分离流动流畅结构和气动特性；TAKAKI 等[9]对多种翼型在火星大气环境下的气动特性进行了研究，发现火星超低雷诺数对翼型气动特性的影响远大于马赫数的影响；MONTEPLARE等[10]利用红外成像技术对螺旋桨在低雷诺数环境下的层流分离现象进行研究，并根据实验结果提出了一种能够在低雷诺数环境中预测层流分离泡的方法；朱志斌等[11]基于低雷诺数环境，采用大涡模拟法(large vortex simulation,LES)方法进行了不同雷诺数下的翼型层流分离数值模拟，详细研究了雷诺数对翼型气动特性的影响；陈水添[12]对火星大气环境下的桨叶的升阻特性进行了研究，并对矩形桨叶的升阻特性进行了实验验证，获得了低雷诺数环境下共轴式旋翼系统产生的升力与单独螺旋桨旋转式产生的升力之间的关系.

文中对几种适用于低雷诺数的翼型在火星超低雷诺数环境下进行气动特性模拟仿真，从而选出适用于火星大气环境的翼型，然后在不同超低雷诺数下对该翼型进行了气动特性仿真与层流分离模拟，用以验证超低雷诺数对翼型空气动力学的影响，最后对轻量化设计的火星螺旋桨进行了地面环境台架实验.

1 适用于超低雷诺数环境的翼型选取

火星低空气密度与低声速导致火星螺旋桨在高速旋转时处于超低雷诺数和高马赫数状态，火星上的雷诺数一般处于Re=103～104范围，在这个雷诺数范围内，普通地球大气环境所用的螺旋桨将不再适用于火星大气环境，而想要设计适应火星超低雷诺数环境的螺旋桨，则首先需要选取能适应火星超低雷诺数环境的翼型.

近年来，已经有一些学者开始探索适应低雷诺数、高马赫数环境的翼型，其中比较典型的翼型有E387翼型[13]、RAE 2822 翼型[14]、SD 8000 翼型[15]、NACA-69 翼型[16]以及CLF 5605 翼型[17]，这些翼型能够较好的适应低雷诺数环境，但对于超低雷诺数环境而言，则还需要进一步探索，本节将通过在超低雷诺数环境下进行数值模拟分析的方法，从几种典型的低雷诺数翼型中选取更适合火星超低雷诺数环境的翼型，表1 展示了上述几种翼型的关键参数.

表1 几种不同翼型的参数Tab.1 Parameters for several different airfoils

1.1 流场仿真参数设置

对于高马赫数、低雷诺数环境而言，在进行翼型绕流仿真计算时，需要考虑流场中出现的分离泡、层流转捩等现象.文中采用Transition SST 转捩模型进行计算，在SSTk-ω模型控制方程基础上进一步求解间歇因子 γ的输运方程和转捩动量厚度雷诺数输运方程，两个输运方程可以表示为[18]

式中： ρ为密度；t为时间；uj为速度在j方向上的分量；xj为坐标值； θ为动量厚度； µ为层流黏性系数； µt为湍流黏性系数；Pγ、Eγ和Pθt的具体形式可以参考文献[19]，方程常数 σγ=1， σθt=2.

转捩模型和SST 湍流模型相结合得到最终的控制方程为

其中：

式中：Pk、Dk分别为原SST 湍流方程的生成项和耗散项.

文中采用ANSYS ICEM 进行网格划分，然后导入到Fluent 里进行二维翼型空气动力学仿真.数值计算翼型的外流域采用C 型，计算域的前半部分是半径为10 倍弦长的半圆，后部分为20 倍弦长的正方形.划分网格时，采用四边形网格.在靠近翼型表面时流场的压强和速度变化比较复杂，因此需要对翼型壁面附近的网格进行加密处理，以便能更好模拟翼型在流场中的复杂气动特性，获得的翼型网格如图1 所示，经网格无关性验证，最终确定网格总数为426 288 个.选择求解器时，由于螺旋桨在火星大气环境高速旋转时马赫数大于0.5，属于可压缩流场，采用密度基求解器更合适.边界条件设置上，则采用压力远场边界条件，能更好地贴合火星大气环境.仿真过程中，认为残差小于10-4时，仿真结果收敛.

图1 二维翼型周围流场的网格划分Fig.1 Meshing of flow fields around a two-dimensional airfoil

1.2 仿真结果分析

通过仿真获取5 种翼型在雷诺数Re分别为1 000、5 000 和10 000 时，攻角α在2°～12°范围内的升力系数Cl、阻力系数Cd、升阻比Cl/Cd和俯仰力矩系数Cm，然后综合比较各项数据，选取适用于火星超低雷诺数环境的最佳翼型.不同翼型的气动特性仿真结果如图2 所示，对5 种翼型在不同雷诺数下的升力系数Cl、阻力系数Cd、升阻比Cl/Cd以及俯仰力矩系数Cm进行分析可知，选用CLF 5605 翼型在火星超低雷诺数环境中具有更大的优势.同时，数值模拟计算的结果也验证了最大厚度范围为2%～6%，最大弯度范围为3%～7%，最大弯度位置为50%～90%的薄翼型更适合低雷诺数环境的结论.

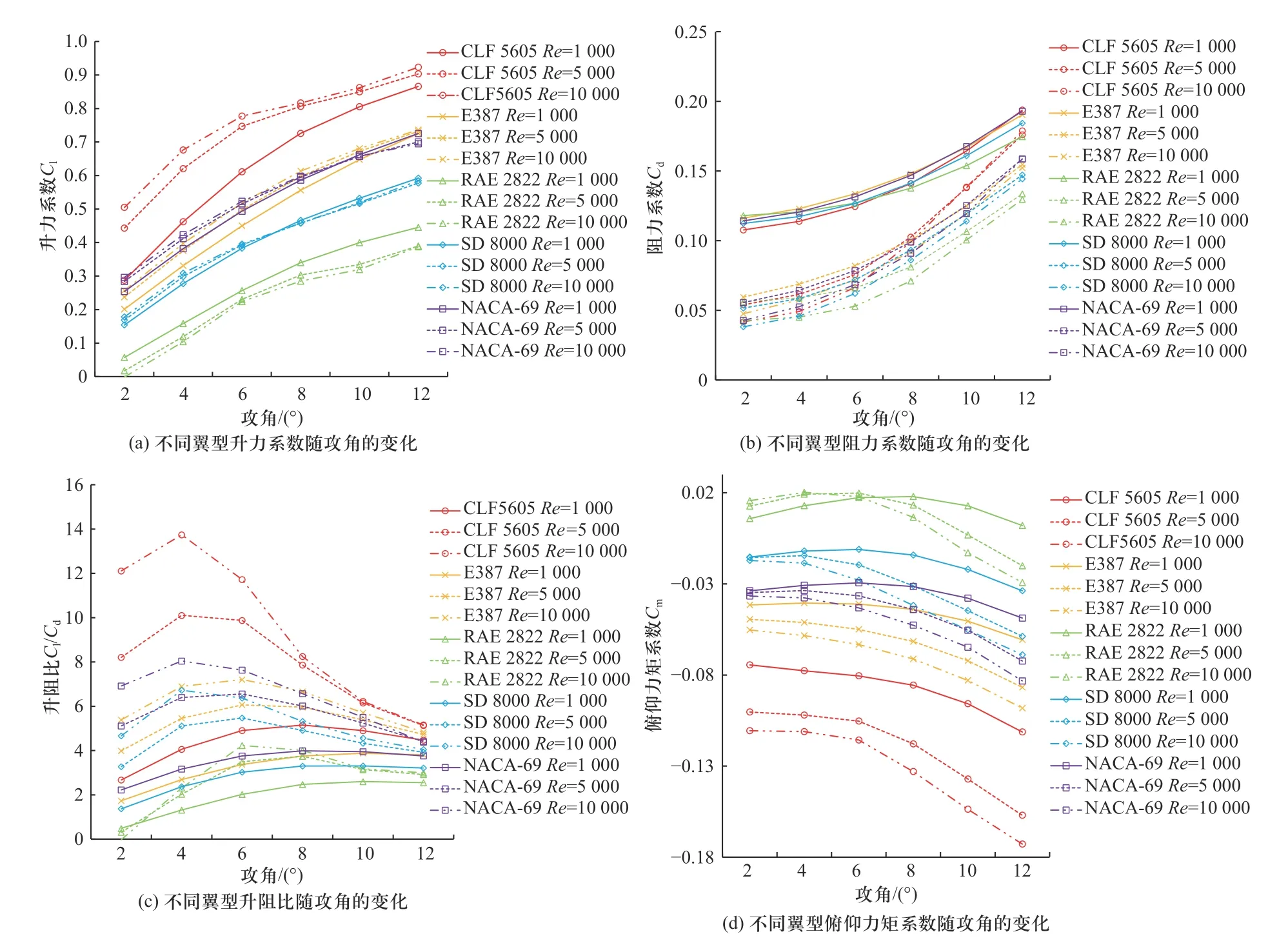
图2 不同翼型在超低雷诺数Re=10 000 时的气动特性Fig.2 Aerodynamic characteristics of different airfoils at ultra-low Reynolds number Re=10 000

2 雷诺数对翼型气动性能的影响

常规飞行器飞行时的Re一般在106量级甚至更高，但火星大气环境则截然不同，无人机旋翼系统的Re一般在103～104范围内运行，这个Re环境相当于地球上3 万米高空处的大气环境，目前，对这个Re环境的研究还处于探索阶段.火星上超低Re环境导致了火星螺旋桨附近气体流动状态的复杂性急剧增加，因此，研究超低Re对火星旋翼机翼型气动性能的影响尤为重要，而Re作为衡量流体流动状态的重要参数，对翼型的气动性能影响十分显著，它反映了惯性力与黏性力间的对比关系[20].Re的减小导致翼型周围边界层变厚，随着迎角的增大，边界层的位移效应引起的曲面有效损失将进一步增大，从而导致升力系数的增长逐渐平缓，甚至当迎角过大时，升力系数呈现减小的趋势，而因为迎角增大导致层流转向湍流，增大了气流对翼型表面的摩擦，导致阻力系数增大.

由上一章节内容可知，CLF 5605 翼型更适用于火星大气环境，本章节通过在不同的火星超低Re环境下对CLF 5605 翼型进行气动分析来阐述Re对翼型气动特性的影响.通过对不同攻角(2°～12°)及不同Re(Re=1 000,Re=10 000)下的CLF 5605 翼型进行CFD 气动特性仿真，其结果表明，同一攻角α下，随着Re的增加，升力系数Cl也随之增加，但升力系数增加的幅度却在逐渐减小，阻力系数Cd随着Re的增大反而降低，这是由于Re增大导致了翼型表面分离气泡后移，从而减弱了阻力，Re越低，阻力系数越大；在同一Re下，随着攻角α的增大，升力系数Cl和阻力系数Cd均随之增大，升力系数曲线在攻角大于4°后，斜率明显减缓，而阻力系数曲线在攻角大于4°后斜率出现明显的增大，而当攻角增加到12°时，无论是升力系数Cl还是阻力系数Cd，不同的Re对应的数值均相差不大，这是由于当攻角增大到一定程度时，层流分离现象对翼型气动特性影响较大造成的；对于升阻比Cl/Cd，同一Re下，随着攻角α的增大，升阻比呈现出先增加后减小的趋势，而在同一攻角下，尤其在攻角小于6°的情况下，升阻比随着Re的增加而增大，在攻角为4°时，升阻比达到最大.攻角大于4°时，升阻比减小的速度随着Re的增大越来越快,这主要归因于阻力系数的显著增加.当攻角到12°时，各Re下的升阻比大致相当.

3 雷诺数对翼型表面层流转捩的贡献

层流分离泡经常出现在低Re气流中，如风力涡轮机、高空飞机或无人机、MAVS 等.在某些情况下，层流分离可以过渡到离体的湍流，并随后重新附着，分离、过渡、再附着的过程即可形成层流分离泡.由于剪切层中流体的波动夹带、逆流边界层的周期性稳定性以及可能形成的涡流结构引起的不稳定，导致层流分离泡可以在翼型上移动.有研究表明，在Re不变的情况下，随着截面升力系数的增大，失稳点在吸力侧向前移动，在压力侧向后移动；随着Re的增加，吸力和压力不稳定位置向前移动，随着凸度的增大，对于所有升力系数，失稳点在吸力侧后移，在压力侧前移.

层流边界层的稳定性与压力梯度直接相关，而压力梯度又受可压缩性气流的影响，层流边界层不能长时间的维持逆压梯度，这很可能导致层流分离[21].目前对于边界层层流分离状态的研究大多是在不可压缩流下进行的，对于可压缩、超低Re环境下，翼型边界层状态的研究还比较少.

由上节结论可知，翼型在4°攻角时具有较高升阻比.因此，本节采用4°攻角、Re为100～20 000 范围进行翼型边界层模拟，其结果如图3 所示,揭示了火星超低Re环境下翼型周围气体流动状态的机理.随着Re的变化，翼型气动特性发生变化的同时，其周围的流动结构也发生了显著变化.在极低Re时，由于螺旋桨的转速较低，所受的逆压梯度较小，因此在翼型周围呈现较厚的层流边界层；随着Re的升高，转速进一步增加，导致翼型上表面逆压梯度增大，层流边界层逐渐减小，层流状态因不能长时间抵抗逆压梯度而开始层流分离，并开始产生层流分离泡；随着Re的进一步增加，层流分离泡逐渐增大，并且尾缘处伴随着湍流出现；当Re逐渐增大到超越临界Re时，翼型周围的层流流动向湍流流动转变.

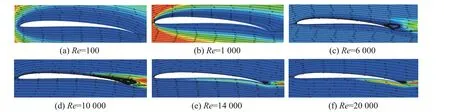
图3 不同Re 下翼型周围的边界层状态Fig.3 The state of the boundary layer around the airfoil under different Reynolds numbers

4 火星大气环境下螺旋桨数值模拟计算

动力系统的设计是火星无人设计的难点之一，火星空气密度相当于地球空气密度的1/80，这也就导致了火星螺旋桨在火星大气密度下所能提供的升力将大幅减小，尽管火星上的重力加速度仅为地球的1/3，但仍不能抵消低空气密度带来的影响.同时，火星上的低声速和以CO2为主的大气成分，进一步限制螺旋桨的转速.根据前面选定的CLF5605 翼型，采用最小能量损失的方法进行螺旋桨设计,将得到的弦长和扭转角进行光顺处理，即可得到火星螺旋桨不同部位的扭转角分布和弦长分布，然后按照所得到的扭转角分布和弦长分布进行螺旋桨三维结构设计，最终得到的火星螺旋桨的桨叶形状如图4 所示.

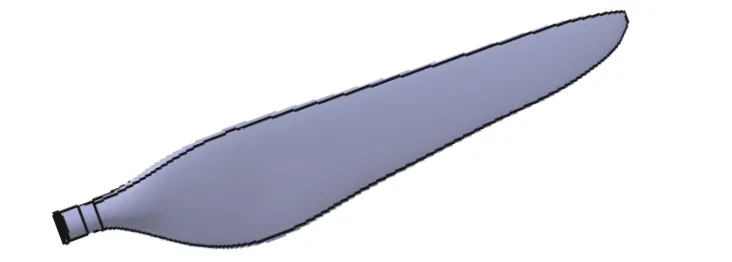
图4 火星螺旋桨的三维模型Fig.4 A 3-dimensional model of a Martian propeller

为了解螺旋桨系统在火星大气环境下的空气动力学特性，采用数值模拟的方法进行螺旋桨气动特性分析.文中采用ICEM 软件进行网格划分，然后在Fluent 软件进行火星大气环境下气动性能数值仿真计算，与前面计算二维翼型气动性能方法相似，将环境设置为火星大气环境，采用Transition SST 模型，密度基求解器，远场边界条件进行数值模拟计算，经网格无关性验证，最终确定网格数量为2 500 万个，数值计算结果如下图5 所示，攻角只取到10°是因为在数值模拟仿真过程中，当攻角大于10°时，计算收敛性较差.其结果显示，同一转速下，随着攻角的增大，螺旋桨产生的升力和扭矩也随之增大，同一攻角时，升力和扭矩随着转速的增大而增大.

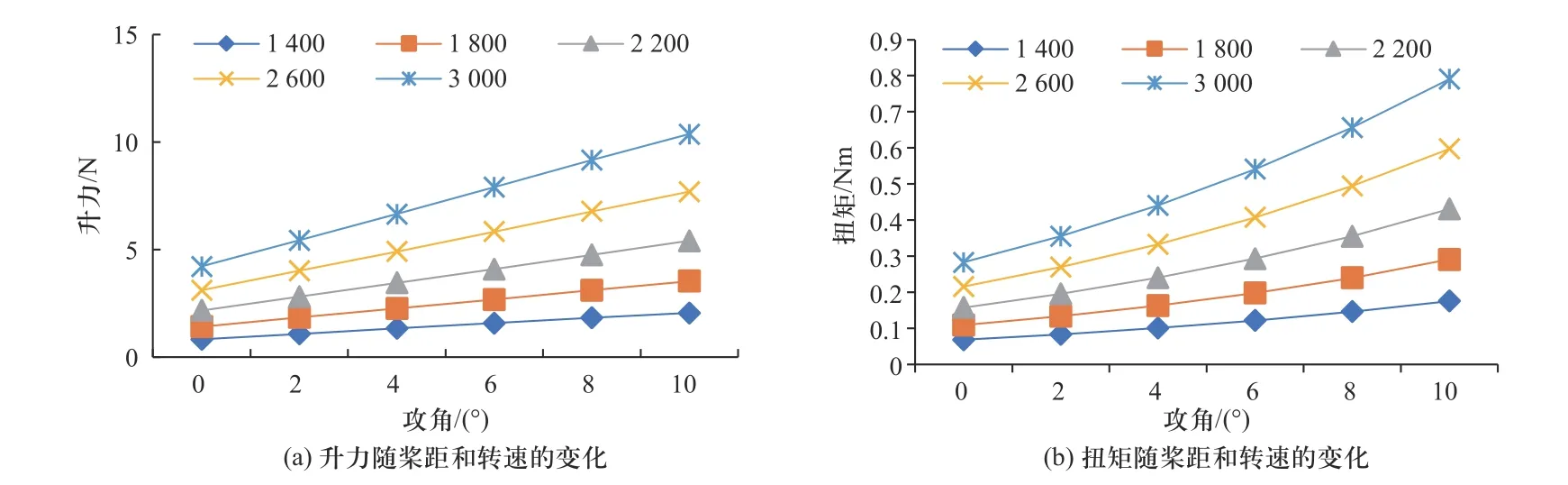
图5 螺旋桨在火星大气环境下的气动性能Fig.5 Aerodynamic performance of propellers in the Martian atmosphere

5 台架实验结果与分析

极低的空气密度给火星螺旋桨的设计制造带来了很大的挑战，火星螺旋桨的一个显著特点就是质量轻，因此轻量化设计在火星无人机的设计中尤为重要.为减轻螺旋桨的质量，在设计时采用了泡沫夹芯结构，中间采用PMI 泡沫层用来维持螺旋桨的形状，然后在泡沫外层铺设三层碳纤维织物铺层，最后在螺旋桨根部进行局部加强，防止螺旋桨在运转时因悬臂梁效应发生断裂，同时能在一定程度上抑制螺旋桨振动[22].

火星的低马赫数、高马赫数环境使得火星无人机旋翼系统的升力、扭矩等参数的变化率远小于旋翼转速的变化率，这对台架测试装置提出了更高的要求，需要测试台架具备足够的准确性和测量精度，能够精确地测量旋翼系统的升力和扭矩.由于火星环境与地球环境差别较大，要进行模拟火星环境真空仓实验，所付出的代价十分昂贵.目前为止，也仅有少数国家或机构进行了相关实验.在进行真空仓台架实验前，进行必要的地球环境实验验证也必不可少， CFD 数值模拟结果与实验结果的双向验证，不仅能检验CFD 数值模拟结果的准确性，也能反映实验测试结果的精确度，同时还能验证轻量化设计的火星螺旋桨在高速旋转时的强度与刚度是否符合要求.地面实验台架设备如图6 所示.主要对螺旋桨在0～2 800 r/min 转速范围、0°～10°攻角范围进行升力以及扭矩的测试.

图6 火星螺旋桨地面台架实验设备Fig.6 Ground bench experimental equipment for Mars propeller

地球环境台架实验结果如下图7 所示，显示了在地球环境中CFD 数值模拟仿真结果与台架实验结果的升力对比，从图中可以看出，不同攻角的升力具有相似性，升力均随着转速的增加而增大.将实验测得的数据进行拟合，即图中的红色曲线，绿色点为CFD 数值模拟结果，可以很清晰地看出，CFD 数值模拟结果基本与实验测试得到的结果吻合，相对误差在10%以内.

图7 不同攻角下升力数值计算结果与实验结果的对比Fig.7 Comparison of lift numerical calculation results at different angles of attack with experimental results

图8 显示了CFD 模拟仿真得到的扭矩与实验测得扭矩的对比，从图中可以看出，随着转速的增加，扭矩的值也相应增大，但CFD 数值模拟得到的扭矩与实验得到的扭矩存在一定的误差，尤其是当攻角增大时，误差越明显，但总体误差不超过15%.

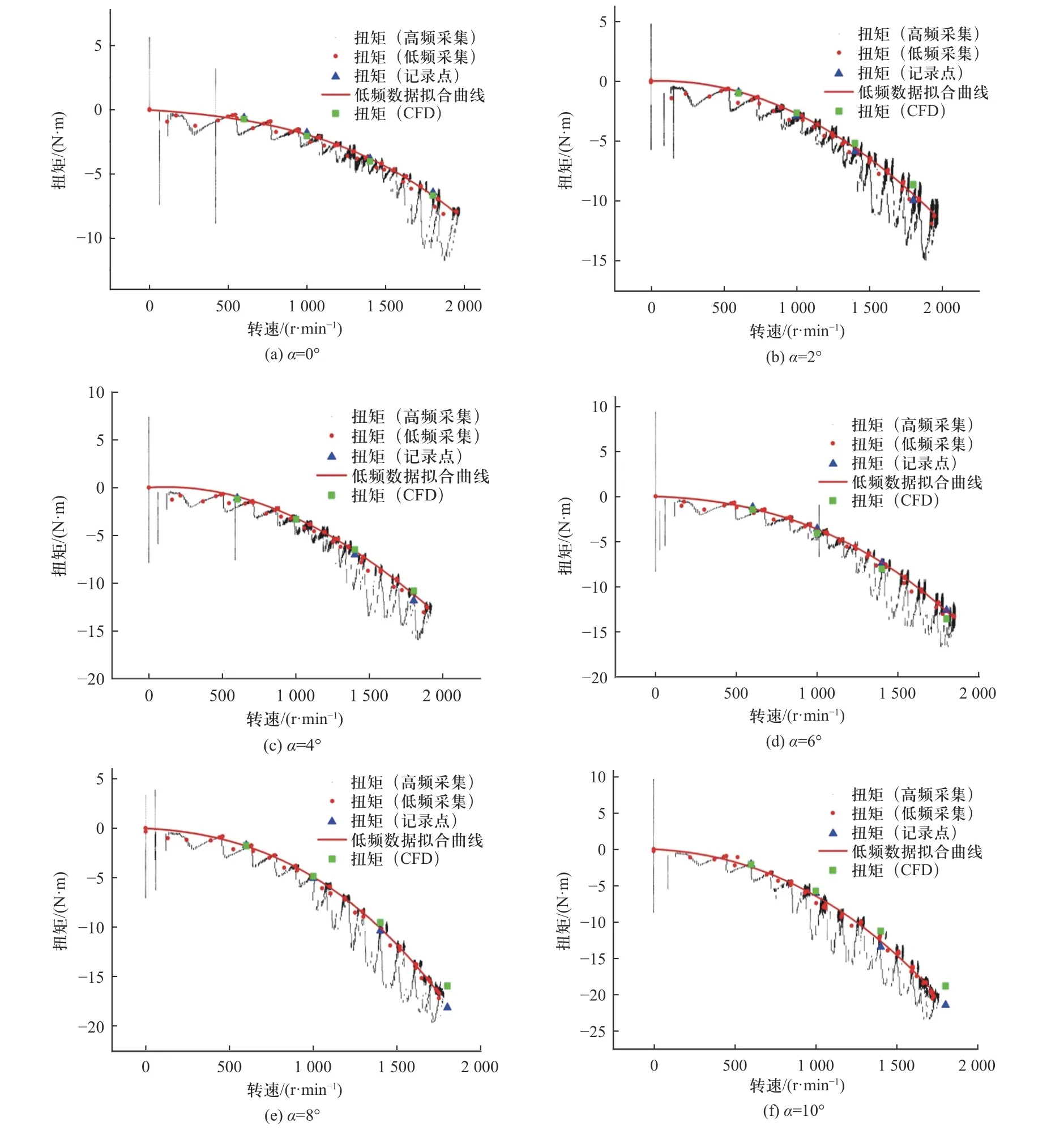
图8 不同攻角下扭矩数值计算结果与实验结果的对比Fig.8 Comparison of the numerical calculation results of torque at different angles of attack with the experimental results

实验结果与CFD 仿真结果存在误差，考虑是由以下因素造成的.

①由于桨叶安装方式、测量方法及测量设备的原因，不能保证实际桨叶角和CFD 计算桨叶角一致，其误差可达0.5°～1°，会造成CFD 计算与试验结果有偏差.

②测试环境是在室外进行的，可能会有风速等外在因素的干扰，造成CFD 仿真计算结果与实验结果存在偏差.

③由于CFD 计算采用MRF 方式对单一工况点进行稳态计算，而MRF 计算方式中的旋转域厚度对旋翼计算结果有较大的影响，尤其对扭矩计算结果影响较大.

通过对火星螺旋桨升力和扭矩的CFD 数值仿真与实验结果的对比可以看出，CFD 数值仿真计算具有很高的准确性，同时实验装备的精确度也足以用来进行模拟火星大气环境真空仓实验.在实验过程中，未见螺旋桨表面有明显损坏，也从侧面验证了轻量化设计火星螺旋桨的强度与刚度满足要求.

6 结 论

针对火星大气超低Re环境，采用ANSYS 数值模拟软件进行火星螺旋桨系统的空气动力学性能仿真，并结合地面台架实验深入研究火星螺旋桨系统的气动性能，研究结果如下：

①对E387 翼型、RAE 2822 翼型、SD 8000 翼型、NACA-69 翼型以及CLF 5605 翼型5 款适合低雷诺数环境的翼型进行火星大气环境下气动性能数值模拟计算，计算结果显示，CLF 5605 翼型在火星超低雷诺数环境中具有更好的空气动力学性能.

②火星大气环境下，对雷诺数Re=1 000～10 000范围内翼型的气动性能进行数值模拟，结果显示，随着雷诺数的增加，翼型的气动性能变得更好，同一雷诺数下，随着攻角的增大，升阻比呈现先增大后减小的趋势，在4°攻角时具有最大升阻比.低雷诺数下，翼型性能的显著下降主要归因于阻力系数的增大.

③超低雷诺数下，翼型周围的边界层状态从低雷诺数Re=100 时的完全层流，到随着雷诺数的增加，边界层逐渐开始出现层流分离、翼型尾缘出现层流分离泡、层流分离泡尺寸增大，最终过渡到湍流的形态.

④采用最小能量损失方法设计螺旋桨，经数值模拟分析，在火星大气环境下具有良好的气动性能，并对轻量化制造的螺旋桨进行了地面台架实验，实验结果与数值仿真结果吻合度较好，意味着轻量化制火星螺旋桨具有较好地强度与刚度、台架实验系统精度满足进入模拟火星大气环境真空仓实验的要求，同时也说明火星大气环境下的数值模拟分析方法能较好地反映出螺旋桨的气动性能.