三维集成TSV 垂直开关研究∗
刘 乐,王凤娟,文炳成,余宁梅,杨 媛
(西安理工大学自动化与信息工程学院,陕西 西安 710048)
随着半导体产业的快速发展,晶体管的特征尺寸减小到纳米量级,各种工艺成本、物理极限、互连延时等问题凸显,传统集成电路的发展遇到了瓶颈[1-4]。三维集成电路可以有效解决此问题,已成为模块级集成的重要途径[5-7]。硅基转接板技术是三维集成的核心技术之一,它利用硅通孔(Through-Silicon Via,TSV)技术实现垂直互连,与传统集成电路完美对接,有效缩短了互连线长,显著提升了性能并减小了面积[4-5]。同时硅基转接板还可制作精细图形,集成无源元件,因此成为了射频/微波等微系统三维集成的重要平台。基于硅基转接板及TSV技术,研究者们相续提出了多种性能优良的电感和电容等无源元件[8-15],但由于缺乏关键的可集成于三维转接板的有源器件,尤其是微型转换开关,因此难以满足现代射频/微波领域多功能模式的要求。针对此问题研究者们提出了有源硅基转接板技术,采用平面有源开关来实现无源器件可配置化,从而实现功能模块的片上调谐[16-19],但在信号通路中插入小尺寸MOS 开关会引入较大信号散射,严重影响系统的完整性,如果采用与之匹配尺寸的传统MOS开关,则占用面积将大大增加。另一方面,将传统开关集成到有源硅转接板中,工艺复杂,成本高,良品率低。因此,载流大、面积小、工艺简单的有源开关成为有源硅基转接板的迫切需求。
针对此问题,德国的Winkler 等[20]首先提出TSV 垂直开关。TSV 垂直开关可以利用垂直空间。相比于传统MOS 开关,TSV 垂直开关具有载流大,面积小、信号噪声小等优点。通过在射频/微波模块中增加一个TSV 垂直开关,可以预期实现高质量片上调谐。然而,关于TSV 垂直开关的理论研究尚未见报道。因此,研究TSV 垂直开关的阈值电压与漏极电流解析模型,为TSV 垂直开关的应用提供理论依据具有重要意义。
1 TSV 垂直开关结构
TSV 垂直开关作为一种新型开关结构,其结构与传统开关有所差别。图1 给出了TSV 垂直开关的三维结构图,图2 给出了TSV 垂直开关的俯视图。
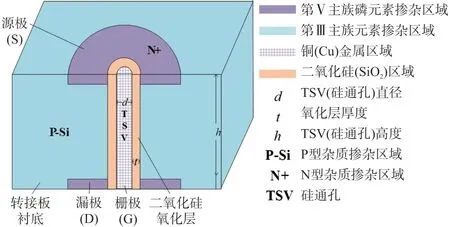
图1 TSV 垂直开关结构示意图
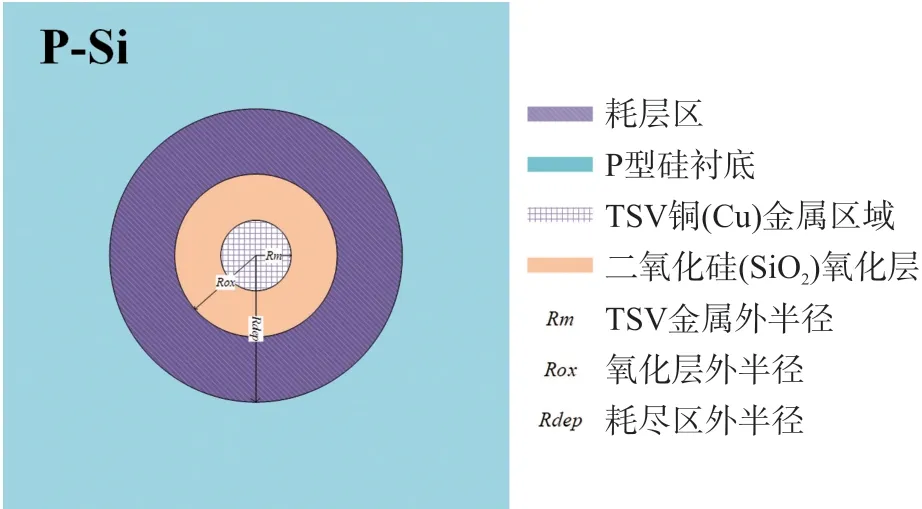
图2 TSV 垂直开关俯视图
结合图1 与图2 可知TSV 金属为穿透P 型硅转接板的铜柱,紧邻TSV 铜柱外侧的氧化层为二氧化硅氧化层,其作用是实现铜与硅转接板之间的电隔离。二氧化硅氧化层外侧的上下端为N 型杂质重掺杂区域。在电学功能上,TSV 垂直开关结构中的TSV 金属铜作为TSV 垂直开关开关的栅极(G),二氧化硅层外上下两端的N 型掺杂区作为TSV 垂直开关的漏极(D)和源极(S),P 型硅转接板作为TSV 垂直开关的衬底(B)。可以看出TSV 垂直开关中的TSV—氧化层—硅转接板三者天然构成了金属—氧化物—半导体(MOS)结构。当栅压(VGS)大于开关的阈值电压(Vth)时,就会在TSV 周围产生从漏极到源极的垂直环型沟道,开关处于导通状态。
2 TSV 垂直开关解析模型
由于TSV 垂直开关为MOS 结构开关,因此TSV垂直开关的阈值电压(Vth)可以定义为当硅衬底-氧化层表面电势等于2VTln(Na/ni)时的栅极电压(VG),由于硅转接板衬底接地,栅极电压(VG)为衬底电势与氧化层内外表面之间电势差Uox之和,其中衬底电势为平带电压VFB与氧化层外围表面电势ψ(Rox)之和,如式(1)所示:
式中:VFB可以根据能带理论得到,如式(2)所示。锥形TSV 的氧化层内外电势差Uox可以通过氧化层表面的电荷量与体电荷数相等计算得到,如式(3)所示[21],式中α为TSV 侧壁与水平线之间角度值。由于本文中研究的是圆柱型TSV 结构,即当α=90°时,圆锥形TSV 演变为圆柱形TSV,所以圆柱型氧化层内外电势差Uox的公式如(4)所示。
当ψ(Rox)等于2VTln(Na/ni)时,结合式(1)、式(2)和式(4)可以得到圆柱型TSV 垂直开关的阈值电压表达式,如式(5)所示:
式中:εox与εsi分别为氧化层与硅衬底的介电常数,Φm为TSV 金属功函数,Φs为硅衬底功函数。Rox、Rm和Rdep分别为TSV 氧化层、TSV 金属和耗尽层的外半径,Na为转接板掺杂浓度,ni为本征载流子浓度,VT为热电压。平带电压VFB中的单位面积氧化层电容Cox为与结构有关的参数,针对TSV 垂直开关的柱形金属栅、环形沟道、环形有源区,单位面积氧化层电容为如式(6)所示[21]:
TSV 垂直开关和二维的MOS 开关区别在于TSV 垂直开关导电区域是三维的环形反型层,二维的MOS 器件的导电区域是在平面反型层,本质没有变化,所以TSV 垂直开关的饱和区和线性区电流可以采用二维MOS 器件计算公式,如式(7)和式(8)所示:
式中:μn为电子迁移率,VGS和VDS分别为栅源电压和漏源电压,宽长比W/L为与结构有关的参数,针对TSV 垂直开关的柱形金属栅、环形沟道、环性有源区,宽长比可以表示为:
式中:tn为源漏区掺杂深度。上述研究均未考虑MOS 管的二级效应且默认转接板衬底接地电压为零,当转接板衬底电压Vb≠0 时,会导致耗尽层厚度和阈值电压变大等后果,会影响整个TSV 垂直开关的电学特性。
3 解析模型验证与分析
本文采用有限元仿真软件Sentaurus 进行器件建模,Sentaurus 中的器件模型三维结构如图3 所示。本文在建模时,将TSV 结构理想化为圆柱型,经计算,当TSV 高度为50 μm 时,夹角α=89.86°,阈值电压为与理想情况误差为1.6%,且误差随TSV高度的减小而减小。实际制造中TSV 侧边与水平夹角α≈90°,TSV 实际结构为圆柱型,因此可以忽略锥型TSV 结构所带来的影响。图4(a)表示了TSV 垂直开关的转接板衬底掺杂情况,由图可知本模型中的衬底所掺杂的杂质元素为第Ⅴ主族元素磷,杂质浓度为5×1015cm-3。图4(b)表示了TSV垂直开关的源漏区域掺杂情况,由图可知本模型中的源漏区所掺杂的杂质元素为Ⅲ主族元素硼,浓度为2×1020cm-3。并以此为固定条件对不同尺寸的TSV 垂直开关进行了电学仿真,其中TSV 垂直开关的TSV 高度(h)、TSV 直径(d)、氧化层厚度(t)均可由现有工艺实现。本文使用MATLAB 软件进行解析模型计算。将仿真所得结果与阈值电压及漏极电流解析模型计算结果进行了对比。其中阈值电压对比结果如表1 所示,漏极电流的转移特性曲线及输出特性曲线分别为图5 与图6,图6 中FEM(Finite Element Method)为有限元仿真曲线,Model 为解析模型计算曲线。
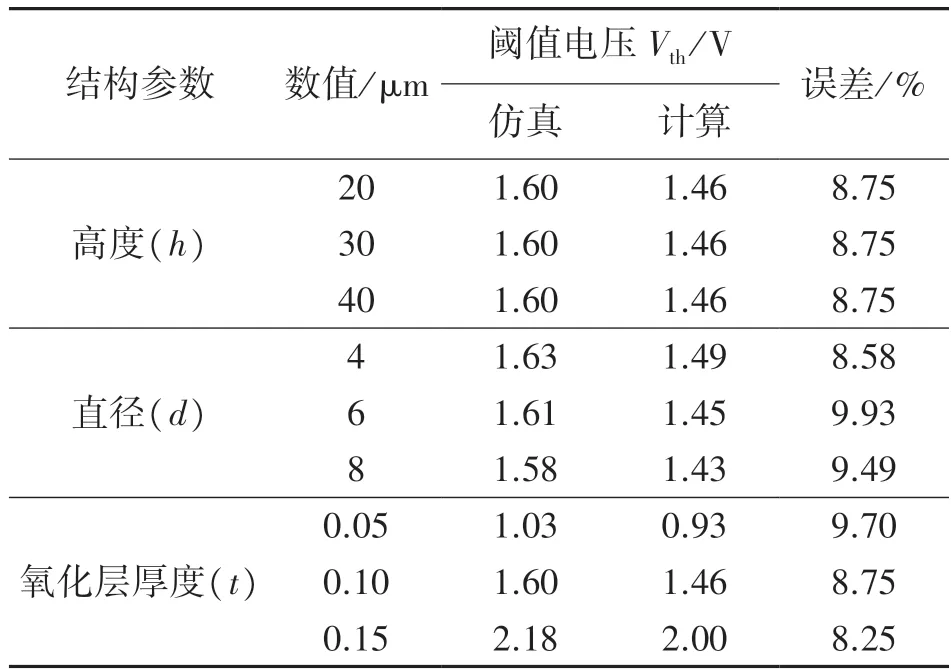
表1 不同参数的阈值电压
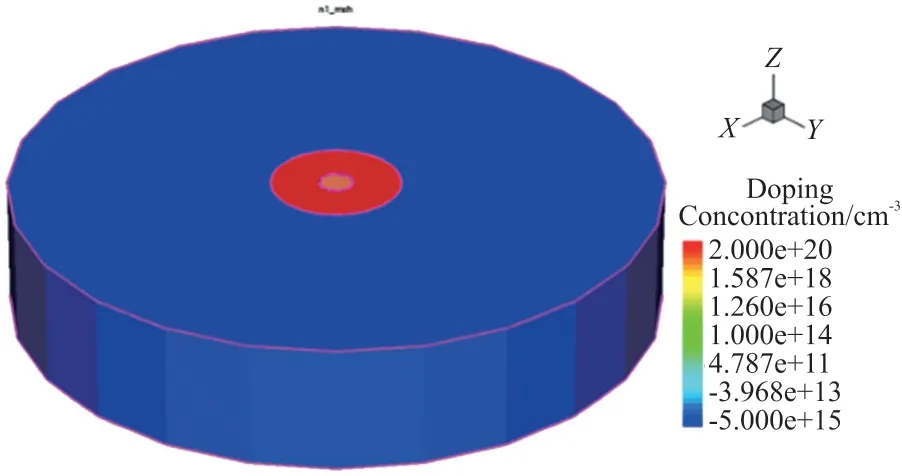
图3 Sentaurus 中的TSV 垂直开关模型

图4 Sentaurus 中的模型掺杂情况

图5 不同参数的开关电流转移特性曲线
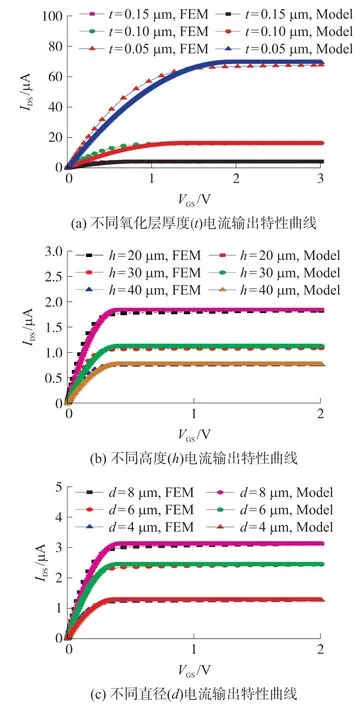
图6 不同参数的开关电流输出特性曲线
由表1 与图3 可知,在漏源电压(VDS)等于0.1 V的条件下,当TSV 直径(d=5 μm)及氧化层厚度(t=0.1 μm)不变时,增大TSV 高度不影响开关的阈值电压;在漏源电压(VDS)等于0.1 V 的条件下,当TSV 高度(h=20 μm)及氧化层厚度(t=0.1 μm)不变时,增大TSV 直径会导致阈值电压的减小,这是因为增大TSV 直径会导致氧化层电容的增大,从而使得阈值电压减小;在漏源电压(VDS)等于0.1 V的条件下,当在TSV 高度(h=20 μm)及TSV 直径(d=5 μm)不变时,增大氧化层厚度会导致阈值电压的增大,这是由于氧化层厚度控制着栅电容的大小,氧化层越厚栅电容越小,栅极对于沟道的调控能力越弱,阈值电压越大。由表1 可知,阈值电压的计算结果一致性小于仿真结果,误差小于10%。是由于采用仿真软件Sentaurus 进行TSV 垂直开关结构建模以及电学特性仿真时,网格的划分以及取值时存在一定误差导致的结果。
图6 为不同参数下的TSV 垂直开关的漏极电流输出特性曲线,其中FEM(Finite Element Method)为有限元仿真曲线,Model 为解析模型计算曲线。由图6(a)可知,在栅源电压(VGS)等于3 V 的条件下,当氧化绝层厚度为0.05 μm、0.10 μm、0.15 μm时,TSV 垂直开关的饱和电流分别为67.9 μA、16.4 μA、4.2 μA,表明TSV 垂直开关的饱和电流随氧化绝缘层的增大而减小,原因是增大氧化绝缘层厚度会导致栅电容减小,进而增大阈值电压,从而使得电流变小。由图6(b)可知:在栅源电压(VGS)等于2 V 的条件下,当TSV 高度分别为20 μm、30 μm、40 μm 时,TSV 垂直开关的饱和电流可达1.8 μA、1.0 μA、0.7 μA,表明TSV 垂直开关的饱和电流随TSV 高度的增大而减小,原因是增大TSV 高度会使得TSV 垂直开关的宽长比减小,从而导致输出饱和电流减小。由图6(c)可知:在栅源电压(VGS)等于2V 的条件下,当TSV 直径为8 μm,6 μm,4 μm 时,TSV 垂直开关的饱和电流分别为3.11 μA,2.43 μA,1.26 μA,表明TSV 垂直开关的饱和电流随TSV 直径的增大而增大,原因是增大TSV直径会使得TSV 垂直开关的宽长比增大,从而导致输出饱和电流的增大。
4 总结
针对三维集成中的TSV 垂直开关,本文提出了它的阈值电压及漏极电流解析模型。用有限元仿真方法进行了模型验证,结果表明误差小于10%。并分析了不同结构尺寸对TSV 垂直开关阈值电压及漏极电流的影响,补全了相关领域的研究空白,为TSV 垂直开关的应用提供了理论参考基础。

