基于FEEMD-NTEO的风电场送出线路故障定位
饶鸿江, 何永泰, 彭 洁, 彭文权
(楚雄师范学院 物理与电子科学学院,云南 楚雄 675000)
0 引言
传统行波检测方法精度低、抗噪能力弱,导致无法精确标定行波波头,行波故障定位方法存在的问题已无法满足电力系统快速切除故障的要求。双馈风电场由电力电子器件直接或间接接入电网,其短路电流具有频率偏移、幅值受限以及正负序阻抗不一致等特点[1],使得以工频相量法为基础的测距技术受到极大挑战[2]。此外,风电资源丰富的区域通常距离负荷中心较远,大规模风电向外输送已成为一种趋势[3]。因此,精确定位故障位置,加快电力系统故障恢复运行,提高风电利用率至关重要。
故障定位方法根据原理主要分为两种[4]:故障解析法和行波法。故障解析法中的单端法采用单端数据进行分析计算,其定位精度受运行方式、过渡电阻等因素的影响[5];双端法利用线路两端的数据进行故障定位计算,但其十分依赖于站间通信设备[6],设备所测出数据是否精确和所上传数据是否能够实时同步将会影响故障定位的结果。为解决双端数据不同步的问题,文献[7]采用计算复杂的精确线搜索比相算法,非同步误差角计算过程中,动态计算分布系数以补偿暂态电流。行波法的故障定位结果是否精准取决于故障行波波头到达检测设备两端的时间是否精准。行波法中被运用较多的方法有小波变换[8-9]和希尔伯特黄变换(Hilbert-Huang Transform,HHT)[10-11]。小波变换法由于计算量大、步骤繁多,因此在实际行波故障定位中不具备很高的运用价值。HHT是通过经验模态分解(Empirical Mode Decomposition,EMD)算法把故障电流行波信号进行分解得到固有模态函数(Intrinsic Mode Function,IMF)分量,从而将不稳定信号和离散信号分解,但该方法计算速度缓慢、定位结果不够精准、模态混叠且抗噪能力,不利于现实中的故障定位。文献[12]提出一种基于EMD与Teager能量算子(Teager Energy Operator,TEO)相组合的故障行波测距算法,相较于HHT,此方法能够快速准确地计算故障距离,但仍未完全克服EMD方法存在的模态混叠和噪声抑制能力差的问题。文献[13]提出一种将集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)与TEO进行结合的故障行波定位方法,在EMD的基础上,对EEMD方法进行改进,去除模态混叠现象,但存在计算时间较长、抗噪能力差的问题。文献[14]在EEMD的基础上提出快速集合经验模态分解(Fast Ensemble Empirical Mode Decomposition,FEEMD),此方法有效解决了EEMD的抗噪能力弱的问题,并且计算速度更加迅速。文献[15]针对EMD分解信号出现模态混叠现象导致信号失真的问题,采用FEEMD减小特征量计算来抑制噪声的影响,使电磁信号的识别率得到较大提升。
综上,本文在EEMD的基础上,通过设置判定标准加快分解速度,并设置阈值去除无用内涵模态分量(Intrinsic Mode Functions, IMF)。引入分辨率参数改进的新型Teager能量算子(New Teager Energy Operator,NTEO),使得FEEMD-NTEO可以达到去除噪声的效果并保留行波信号的完整性,计算耗时也更短。提出一种基于FEEMD-NTEO的风电场送出线路行波故障定位方法,并与FEEMD-TEO、EEMD-NTEO方法进行仿真比较。结果表明,三种方法都具有较高的定位精度,但FEEMD-NTEO方法抗噪能力更强、定位实时性更好并且可快速准确地计算出故障距离。
1 FEEMD-NTEO原理
1.1 FEEMD原理
文献[16-18]提出一种以EMD为基础的新分解方法,即EEMD。EEMD算法存在计算量大、计算时间较长、实时性差[19]以及迭代过程多次在原始信号中混入白噪声,分解完后存在噪声残余[20]的缺点。因此,为提高算法效率,文献[19]提出了基于EEMD的改进算法FEEMD。FEEMD通过优化停止条件减少筛选次数来提高算法的执行效率,且能较好地对信号进行去噪。实际上大多数信号是复杂的、非平稳的,FEEMD将信号分解为有限个IMF分量和剩余分量R,分解后既可以保留信号完整性又能达到去除噪声的目的,也能降低计算时间,主要计算步骤如下:
(1) 先分别求出时序数据Xi(t)的极大值和极小值,再以3次样条插值方法得到上下包络线Ui(t)和Li(t),并求出Ui(t)和Li(t)的均值mi(t)。
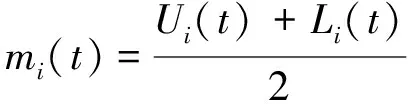
(1)
(2) 求出mi(t)与Xi(t)之间的差值。
hi(t)=Xi(t)-mi(t)
(2)
需判断hi(t)是否满足以下条件:①一个序列的零点数目和极值数目须相等,或两个序列的零点数目和极值数目不超过一个;②在任意时刻点,上包络线与下包络线的平均值均为0。
(3) 计算剩余数据。
ri(t)=Xi(t)-hi(t)
(3)
重复以上步骤,获取N个IMF分量。
分解过程中停止分解的判断标准如式(4)所示:

(4)
式中:m为筛选次数;n为样本数。
综上可得Xi(t)的表达式如式(5)所示:

(5)
式中:N为IMF分量总个数;RN(t)为余项。
设定门限阀值并处理尺度上无用的IMF1分量,软限幅函数如式(6)所示:
η1(t)=
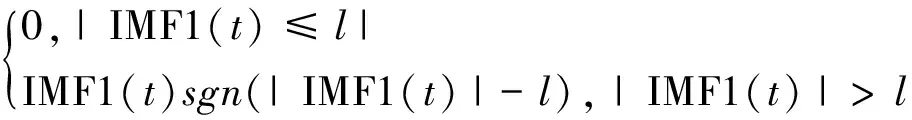
(6)
式中:η1(t)为经阀值处理后的IMF1分量,已去除某些尺度上的噪声;l为时序数据阀值,其表达式为
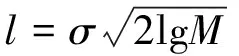
(7)
式中:σ为噪声的方差;M为加噪信号长度。
1.2 NTEO原理
Kaiser提出计算信号瞬时能量的非线性算子:Teager能量算子(TEO)。其常被用于信号处理,对于连续时间信号,TEO定义如式(8)所示[21]:
ψc[s(t)]2=[s′(t)]2-s(t)s″(t)
(8)
式中:ψc[s(t)]为能量算子;s(t)为时间信号。
在实际应用中,采样信号为离散信号,可进行差分运算,定义能量算子为
ψ[s(n)]=s2(n)-s(n+1)s(n-1)
(9)
TEO对噪声的抗干扰能力较弱,所以在噪声环境下TEO算法得到的定位结果可能不够精确。本文采用NTEO能量算子作为信号处理方法。该算法可以有效增强信号在频域中的特性,提高TEO的抗噪声能力,通过加入分辨率参数i,并利用前后相差i点的3个点进行能量值计算,计算表达式为
ψ[s(n)]=s2(n)-s(n+i)s(n-i)
(10)
由式(9)、(10)可知,TEO和NTEO都采用3个点进行能量值计算,但是后者在算法中引入分辨率参数i,增强了TEO能量算子对信号的敏感度,从而提升了NTEO算法对噪声的抗干扰能力。
2 FEEMD-NTEO行波故障定位法
FEEMD-NTEO行波故障定位法的具体步骤如下:
(1) 采集系统侧和风电场侧三相电流行波数据IA、IB、IC;
(2) 通过卡伦鲍尔变换,提取行波电流线模分量;

(11)
式中:Iα、Iβ分别为线模、β模分量;I0为零模分量。
(3) 对电流行波线模分量进行FEEMD分解,获取IMF1分量;
(4) 计算IMF1分量的NTEO能量值;
(5) 根据NTEO能量谱,NTEO能量值最高点对应时刻即为行波波头到达时刻;
(6) 标定行波波头达到时刻,根据式(12)计算故障点到系统侧的距离。

(12)
式中:tM1为行波波头到达系统侧即M端的时间;tN1为行波波头到达风电场侧即N端的时间;l为系统侧和风电场侧之间的距离;v为行波波速;lMF为系统侧与故障点F之间的距离。
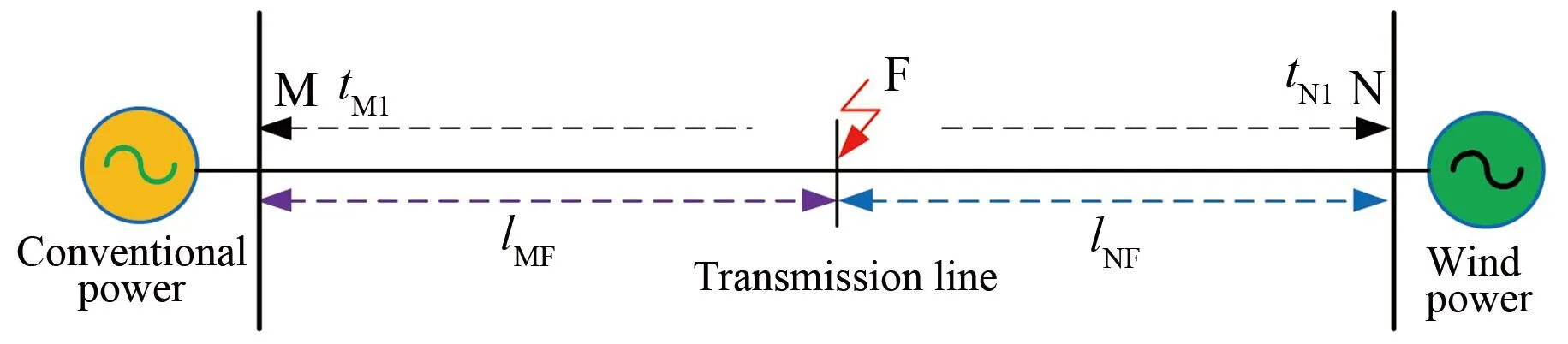
双端行波故障定位原理图如图1所示。

图1 双端行波故障定位原理图
3 仿真分析
3.1 仿真模型
双端行波故障定位法精度和可靠性较高,但需要在线路两端安装行波检测装置,因此造价较高。为保证较高的故障定位精度,应精确标定行波波头到达线路两端的时间,所以在实践中需要利用高精度的北斗系统实现采样数据精确同步。为验证本文所提方法的可靠性和精确性,采用如图2所示的双馈风电场送出线路进行故障定位仿真验证。

图2 风电场送出系统仿真模型
仿真模型中双馈风机单机额定容量为1.5 MW,总台数200台,风电场总容量为300 MW;机端额定电压为0.6 kV,额定频率为50 Hz;定子电阻为0.015 7 p.u.,定子电感为0.325 p.u.,转子电阻0.016 p.u.,转子电感0.16 p.u.,撬棒电阻为0.004 5 p.u.;风电场箱变额定容量为2.5 MVA,电压等级为35 kV/0.69 kV,DYN接线;主变额定容量为350 MVA,电压等级为220 kV/35 kV,YN接线;送出线路长度为100 km,单位长度正负序阻抗为0.082+j0.342 Ω/km、零序阻抗0.221+j0.787 Ω/km,采样率为1 MHz。
故障定位仿真计算时间取决于电脑硬件配置,为更好进行仿真验证,计算机配置为:CPU为i5-12450 H,主频为2.0 GHz,内存为16 G。
采用电流行波线模分量,在系统侧和风电场侧进行电流行波检测,利用卡伦鲍尔变换对电流行波进行解耦,提取系统侧和风电场侧的电流行波线模分量,如图3所示。

图3 系统侧和风电场侧电流行波线模分量
3.2 电流行波FEEMD分解
设定参数:噪声与待分解信号标准差之比Nstd=0.01,对信号的平均次数NE=8。采用FEEMD算法对系统侧和风电场侧的电流行波进行分解后,尺度上无用的IMF1分量可以通过设定阀值来筛除,既保留行波特征信息的完整性又能去除噪声;再采用NTEO能量算子对IMF1分量去噪,使行波波头的标定更精确。设置距离系统侧60 km处发生A相金属性接地故障,电流行波FEEMD分解如图4所示。
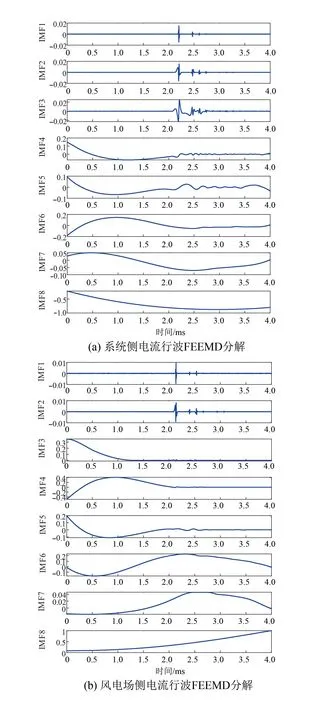
图4 电流行波FEEMD分解
3.3 电流行波能量谱
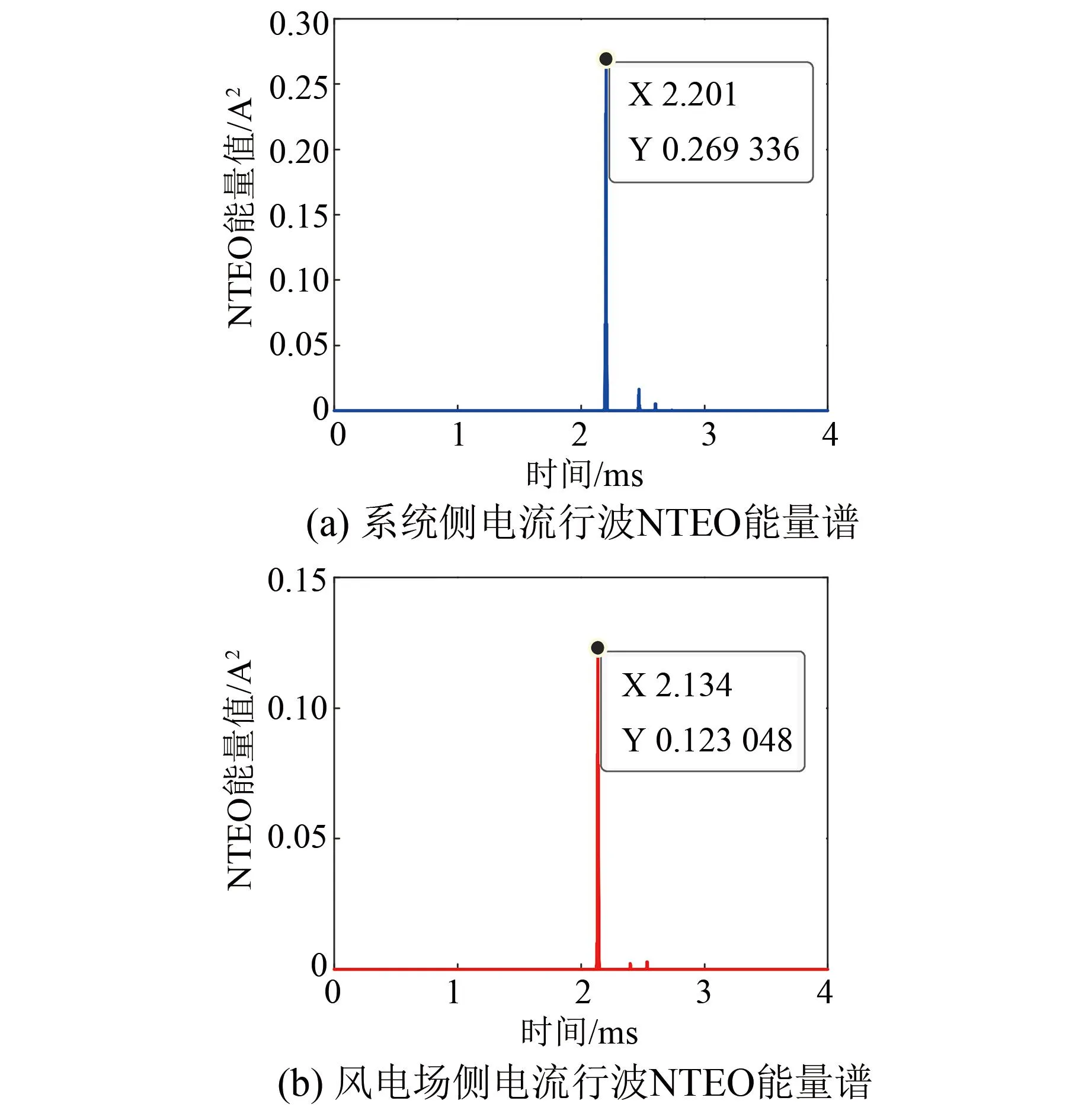
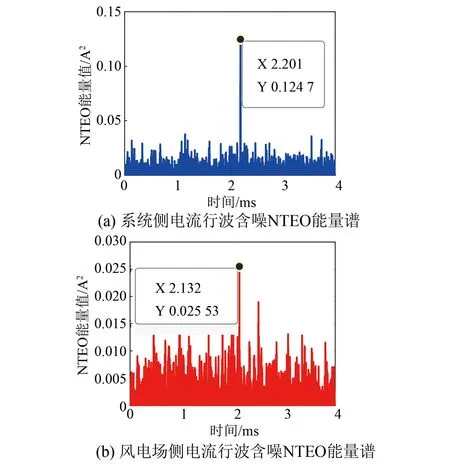
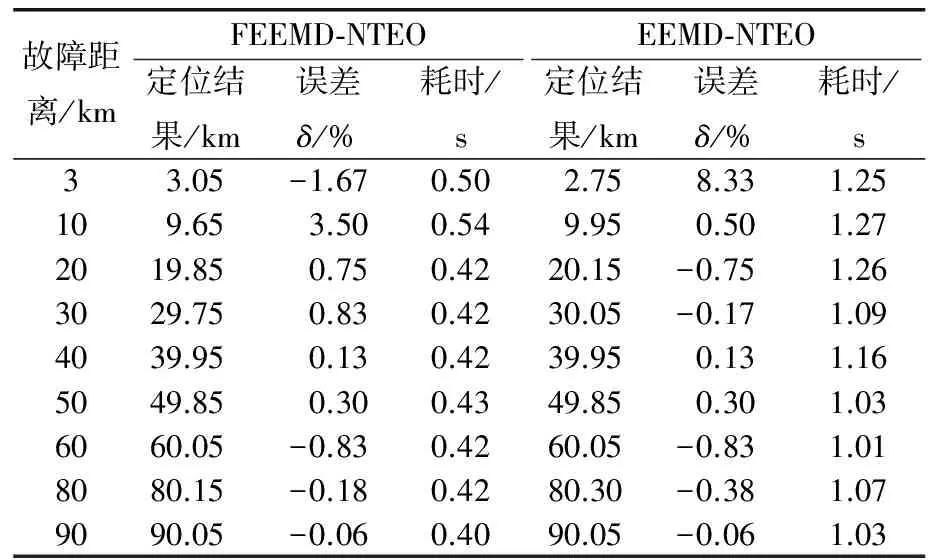
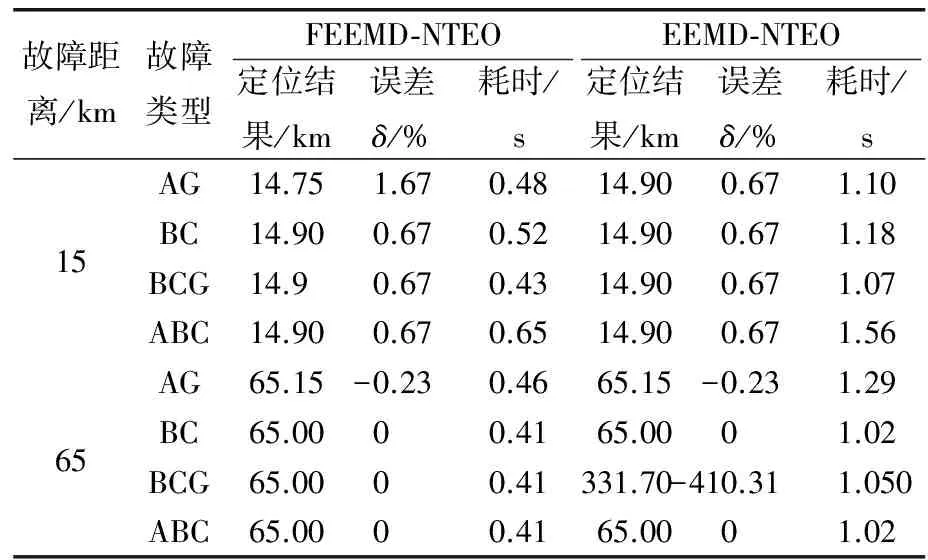
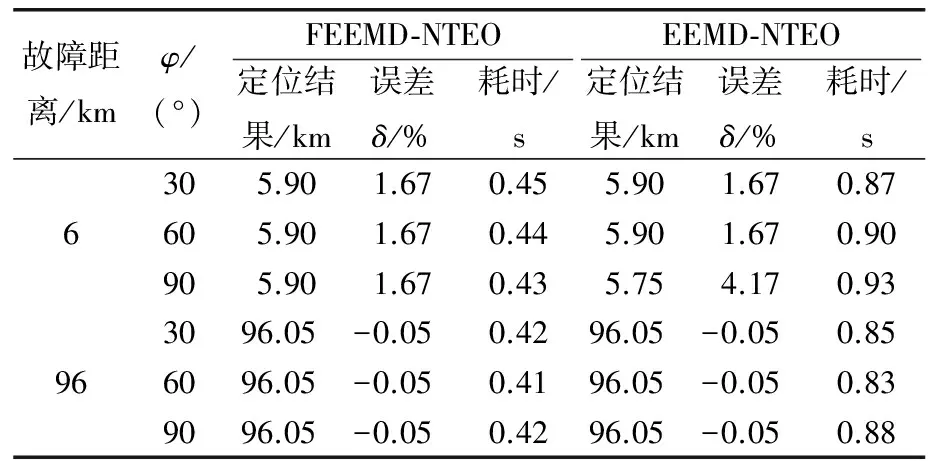
采用FEEMD分解后,提取行波信号中的IMF1分量,利用NTEO能量算子计算IMF1分量,即可得到IMF1分量的能量谱。能量谱中,能值最大值点对应时刻为行波波头到达系统侧和风电场侧的时间。NTEO能量算子中分辨率参数i应满足i 表1 不同分辨率参数i下的定位精度 由表1可知,根据多次仿真结果,选取分辨率参数i=5较合适。实际上,当采样频率fs发生改变时,分辨率参数i应重新选取最优参数值。 假设在距离系统侧60 km处发生A相金属性接地故障,系统侧和风电场侧采用FEEMD和EEMD分解的IMF1分量NTEO能量谱分别如图5和图6所示。 图5 FEEMD分解电流行波NTEO能量谱 图6 EEMD分解电流行波NTEO能量谱 由图5和图6可知,FEEMD-NTEO算法检测到故障行波波头到达两侧的时间分别为tM1=2.201 ms、tN1=2.134 ms。EEMD-NTEO算法检测到故障行波波头到达两侧侧的时间和FEEMD-NTEO算法相同。由式(12)计算可得故障点距离系统侧60.05 km,误差为50 m,上述两种方法都有较高的定位精度。 为验证本文所提故障定位方法具有良好的实用性,而且为更贴近工程实际情况,在系统侧和风电场侧电流中加入30 dB的高斯白噪声,将FEEMD-NTEO、FEEMD-TEO以及EEMD-NTEO三种算法进行对比。假设在距离系统侧96 km处发生A相金属性接地故障,加入噪声后的系统侧和风电场侧电流行波如图7所示。 图7 两侧电流行波(含噪声) 采用FEEMD分解的两侧电流行波含噪IMF1分量NTEO能量谱如图8所示。 图8 FEEMD分解电流行波含噪NTEO能量谱 采用FEEMD分解两侧电流行波含噪IMF1分量TEO能量谱如图9所示。 采用EEMD分解两侧电流行波含噪IMF1分量NTEO能量谱如图10所示。 图10 EEMD分解电流行波含噪NTEO能量谱 由图8~10可知,故障信号含有强噪声,FEEMD-TEO算法采用的是TEO能量算子,FEEMD分解虽不彻底,但保留了信号的完整性,存在少部分噪声干扰的情况下波头难以精准标定,定位结果为48.4 km,结果失效。EEMD-NTEO算法虽然在一定程度上能够抑制模态混叠,但并没有完全消除,残余噪声的存在使定位失败,定位结果为126.65 km。FEEMD-NTEO算法中的NTEO相比于TEO去噪能力强,FEEMD分解在保留信号完整性的前提下,行波突变点明显,所以该算法能够精确标定波头,故障定位结果为95.3 km,误差为700 m。FEEMD-NTEO算法计算耗时0.589 4 s,EEMD-NTEO法计算总耗时1.190 3 s,可见相较于EEMD-NTEO算法,FEEMD-NTEO算法行波检测实时性更好。 以距离系统侧60 km处发生A相金属性接地故障为例,线路两侧采样电流行波中含有40 dB高斯白噪声的故障定位结果如图11和12所示。图11采用FEEMD-NTEO算法,定位结果60.35 km,图12采用FEEMD-TEO算法,定位结果81.35 km。NTEO、TEO能量算子虽然都采用三个点计算,但NTEO算法引入的参数i增强了行波信号的依频特性,抑制噪声的能力比TEO算法强。因此FEEMD-NTEO行波检测结果更为准确。 综上所述,噪声能量不可忽略时,NTEO算法的去噪效果比TEO算法好。信号不含噪声时FEEMD-NTEO算法与EEMD-NTEO算法定位结果都比较精确,但在抗噪能力上FEEMD-NTEO算法比EEMD-NTEO算法强。考虑到实际现场会有大量噪声干扰,所以本文所提的基于FEEMD-NTEO算法的故障定位方法更适用于实际现场。 图11 FEEMD分解电流行波含噪NTEO能量谱 图12 FEEMD分解电流行波含噪TEO能量谱 3.4.1 不同故障距离的影响 考虑到不同的故障距离可能会对结果产生影响,所以选择分别在距系统侧3、10、20、30、40、50、60、80、90 km处设置A相接地故障,过渡电阻为50 Ω,进行验证,其结果如表2所示。由表2可知,采用FEEMD-NTEO算法和EEMD-NTEO算法都有较高的定位精度,受故障距离的影响较小,但FEEMD-NTEO算法耗时短,实时性更好。 表2 不同故障距离下的定位结果 3.4.2 不同过渡电阻的影响 过渡电阻越大,行波幅值衰减速度越快,行波到达系统侧和风电场侧的波头幅值会有所降低,可能会对测距结果造成影响。因此将分别在5和96 km处设置单相接地故障,对过渡电阻分别为10、40、80、100、200、300 Ω的情况进行仿真验证,故障定位结果如表3所示。由表3可知,两种方法的定位结果基本一致,不受过渡电阻的影响,过渡电阻发生变化时,故障定位相对误差基本不变,但在故障定位计算时长上本文所提算法比EEMD-NTEO算法耗时更短,故障定位速度更快。 表3 不同过渡电阻下的定位结果 3.4.3 不同故障类型的影响 为验证不同故障类型的影响,本文在距离系统侧15、65 km处,分别设置ABC三相短路、A相接地短路、BC相间短路、BC两相接地短路。不同故障类型下测距结果如表4所示。由表4可知,两种方法的定位结果基本不受不同故障类型的影响,但EEMD-NTEO算法在65 km处的BC两相接地短路的故障情况下定位失效。其它故障类型下上述两种方法仍然可以保证很高的测距精度,且本文所提算法比EEMD-NTEO算法耗时更短。 表4 不同故障类型下的定位结果 3.4.4 不同故障相角的影响 考虑到不同的故障相角可能会对测距结果造成影响,所以选择在距离系统侧6、96 km处分别设置30°、60°、90°的故障相角,测距结果如表5所示。由表5可知,两种方法都不受故障相角的影响,都具有较高的定位精度,但FEEMD-NTEO算法比EEMD-NTEO算法定位耗时更短。因此FEEMD-NTEO算法更适用于送出线路的故障定位,能够加快恢复故障运行。 表5 不同故障相角下的定位结果 针对EEMD用于双馈风电场送出线路行波故障定位中行波检测精度不高,出现模态混叠、抗噪能力弱以及故障定位实时性差等问题,本文提出一种基于FEEMD-NTEO的双馈风电场送出线路行波故障定位方法。通过仿真验证,得出如下结论: (1) 所提FEEMD-NTEO算法与EEMD-NTEO算法都有较高的定位精度,但在故障信号含大量噪声的情况下,采用FEEMD-NTEO算法可以消除部分噪声,保留行波突变特征,定位精度能满足实际工程需求。 (2) 针对不同故障距离、故障相角、过渡电阻以及故障类型等故障情况进行仿真对比。结果表明,所提算法受故障距离、过渡电阻、故障类型及故障相角的影响较小,定位结果具有可靠性高、精度高且实时性好等优点,可应用于风电场送出线路故障定位中。强噪声环境下相较于FEEMD-TEO、EEMD-NTEO算法,本文所提的FEEMD-NTEO算法定位结果更可靠,实用性更强。 Fault Location of Wind Farm Transmission Line Based on FEEMD-NTEO RAO Hongjiang, HE Yongtai*, PENG Jie, PENG Wenquan (Department of Physics and Electron Information Science, Chuxiong Normal University, Chuxiong 675000, China) Keywords: wind farm; transmission line; fault location; fast ensemble empirical mode decomposition and novel Teager energy operator (FEEMD-NTEO) The traditional traveling wave detection method has low accuracy and weak anti-noise ability, which makes it impossible to accurately calibrate the traveling wave head. The problems existing in the traveling wave fault location method have been unable to meet the requirements of fast fault removal in power system. The doubly-fed wind farm is directly or indirectly connected to the power grid by power electronic devices. Its short-circuit current has the characteristics of frequency offset, limited amplitude, and inconsistent positive and negative sequence impedance, which makes the ranging technology based on the power frequency phasor method greatly challenged. Therefore, it is crucial to accurately locate the fault location, speed up the fault recovery operation of the power system and improve the utilization rate of wind power. In this paper, the ensemble empirical mode decomposition is applied to the traveling wave fault location of the doubly-fed wind farm transmission line. And a traveling wave fault location method based on fast ensemble empirical mode decomposition and improved novel Teager energy operator is proposed. This method uses FEEMD to decompose the fault current traveling wave signal into stationary intrinsic mode components and residual components, eliminates noise components, and preserves the integrity of the signal. Then, the NTEO algorithm is used to denoise the decomposed high-frequency signal again, enhance the fault traveling wave mutation characteristics, and accurately calibrate the traveling wave head. In order to ensure high fault location accuracy, the time when the traveling wave head reaches both ends of the line should be accurately calibrated. Therefore, it is necessary to use high-precision Beidou system to achieve accurate synchronization of sampling data in engineering. In order to verify the reliability and accuracy of the proposed method, the simulation model of the doubly-fed wind farm transmission system shown in Fig.1 is used to verify the fault location. Fig.1 Simulation model of wind farm outgoing system The simulation analysis is carried out for different fault conditions such as different fault distance, fault phase angle and transition resistance. The simulation results show that both the proposed method and the EEMD-NTEO algorithm have high positioning accuracy. However, in the case of a large amount of noise in the fault signal, the FEEMD-NTEO algorithm can eliminate some noise and retain the mutation characteristics of the traveling wave, so the positioning accuracy can meet the actual engineering requirements. The proposed algorithm is less affected by fault distance, transition resistance, fault type and fault phase angle. The positioning results have the advantages of high reliability, high precision and good real-time performance, which can be applied to the fault location of wind farm transmission line. In the strong noise environment, compared with the FEEMD-TEO and EEMD-NTEO algorithms, the FEEMD-NTEO algorithm proposed in this paper is more reliable and practical in localization results.


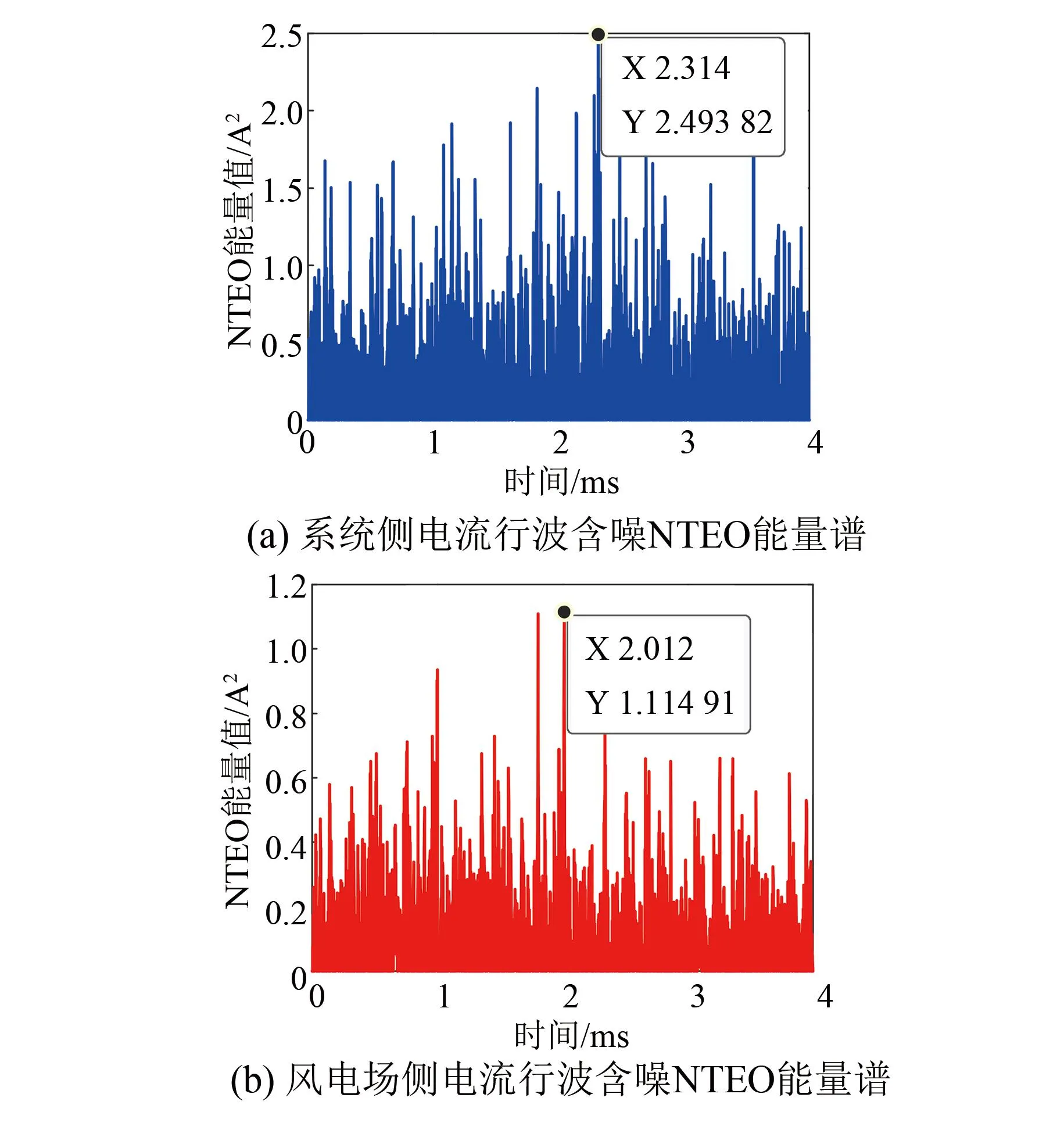
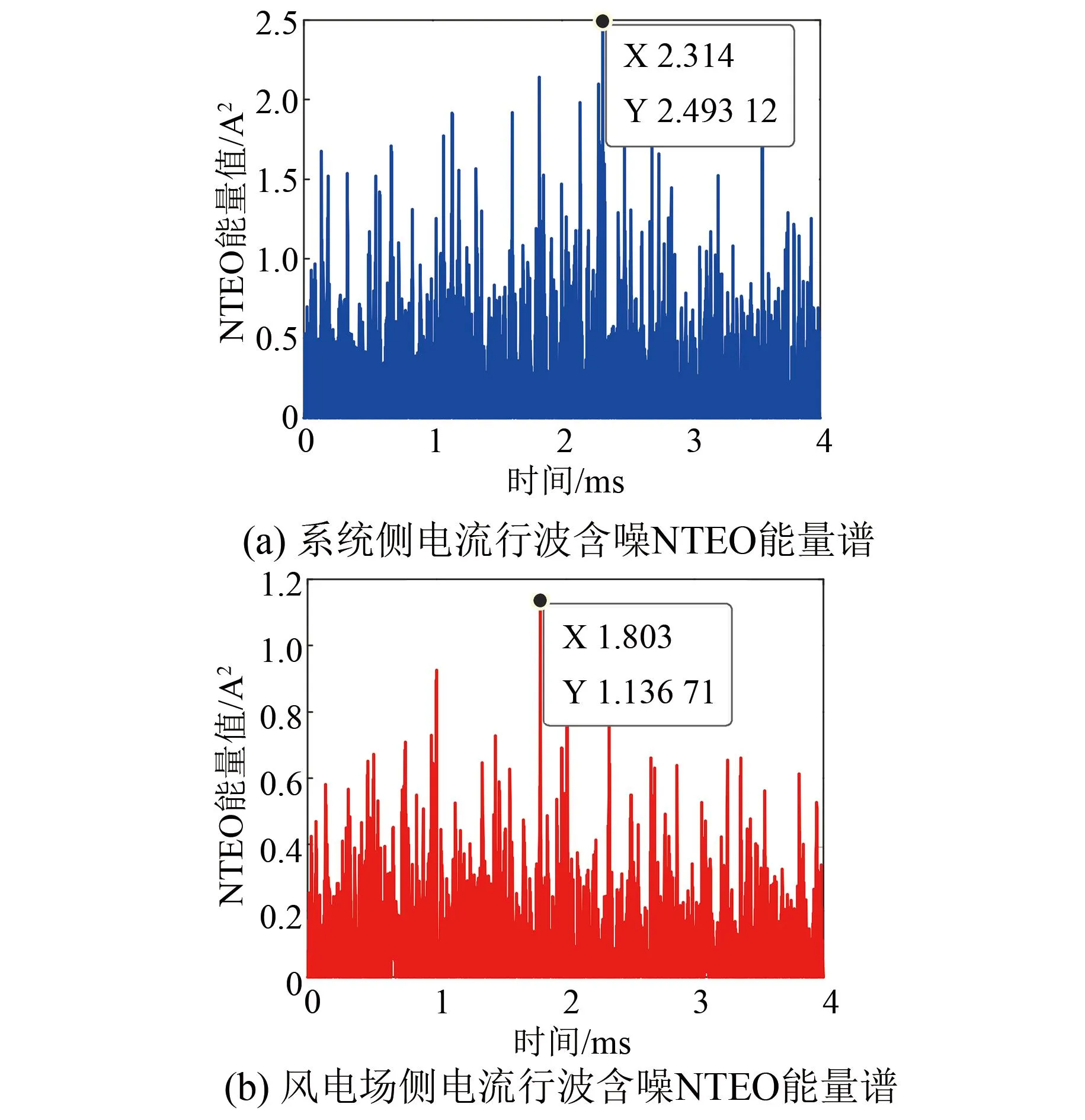

3.4 不同故障情况下的仿真验证

4 结语