永磁同步电机改进型全阶滑模观测器无传感控制

宋建国, 李子豪, 刘小周

(北京工业大学 信息学部,北京 100124)

0 引言

永磁同步电机以其结构简单、体积小、质量轻、损耗小及效率高等优点,被广泛应用于新能源汽车、无人机和机器人控制等领域[1]。为节省成本,减去传感器安装的繁琐步骤,无位置传感器的控制方式越来越受到研究者们的关注[2]。

无位置传感器的控制方式主要分为中高速基于电机反电势和低速凸极跟踪两种方法[3]。本文主要研究基于中高速的电机控制方式。

在电机高速的控制方式中,由于滑模观测器具备鲁棒性较强、响应速度快的优点[4],其在无位置传感器永磁同步电机转子位置和转速估计中得到了广泛应用。但是传统的二阶滑模观测器由于bang-bang控制函数的存在,其在运行过程中存在系统抖振问题[5],同时观测出的电机反电势需要通过低通滤波器获得,因此得到的转子位置需要进行一定的相位补偿,增加了控制系统的复杂性。因此,解决滑模观测器存在的抖振问题以及补偿角度的问题显得尤为重要。文献[6]将传统的符号切换函数改成了sigmoid函数,同时对滤波器进行改进,减少了系统噪声。文献[7]在传统的幂次趋近律的基础上引入了Fal函数,削弱了电机转动过程中的抖振现象。文献[8]设计了自适应的滤波器,从中提取出需要的扩展反电动势,极大减少了观测角度的相位延迟,保证了转子观测的准确性。文献[9]将改进的二阶广义积分器作为滑模观测器的滤波器,其具有很好的高频干扰信号抑制能力。文献[10]基于有限元仿真和遗传算法对滑模的参数进行优化,减弱了系统的抖振。

针对传统全阶滑模观测器在运行过程中存在系统抖振、观测精度低的问题,本文提出了一种变边界层厚度的永磁同步电机全阶滑模控制方法。为减少系统抖振,将全阶滑模的sign函数替换成变边界层的sin函数,同时为了提高系统的鲁棒性,将滑模的增益与转速联系起来,提高了滑模观测器的估计精度。

1 永磁同步电机数学模型

永磁同步电机的数学模型是分析电机的重要手段,通过电机的数学方程可以很好地对电机进行控制分析[11]。永磁同步电机是一个多变量、强耦合的非线性系统,所以其数学模型相对复杂。为了简化永磁同步电机的建模分析,忽略铁心的涡流损耗和磁滞损耗,忽略电机绕组漏感,假设永磁体产生的气隙磁场以正弦波分布在气隙空间中。在此基础上,建立在静止坐标系(α-β)下的电机数学方程,即[12]：

(1)

式中：uα和iα分别为α轴上的电压和电流分量;uβ和iβ分别为β轴上的电压和电流分量;Ld和Lq分别为电机的直轴电感和交轴电感;ωe为电机的电角速度;Rs为电机的定子绕组电阻;eα、eβ分别为α轴和β轴上的扩展反电势。

(2)

式中：ψ为永磁体磁链(永磁体磁链矢量的方向与d轴相同);θe为电机的电角度。

从式(2)中可以看出,电机的扩展反电动势包含电机的转子位置和电机转动的电角速度。因此将eα、eβ观测出来即可求得电机的转子位置和转速[13]。

2 传统的全阶滑模观测器

为减少整个系统的抖振,简化整个系统的结构,将电机的扩展反电势加入电流观测器中,构建全阶滑模观测器。

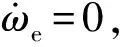
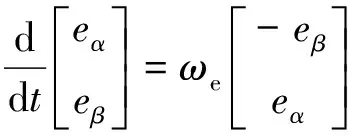
(3)

将式(3)的反电动势方程代入原来的电机方程中,可得电机的全阶方程为

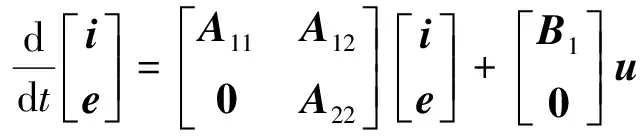
(4)

式(4)建立的全阶滑模观测器包括电流观测器和扩展反电动势观测器：

(5)

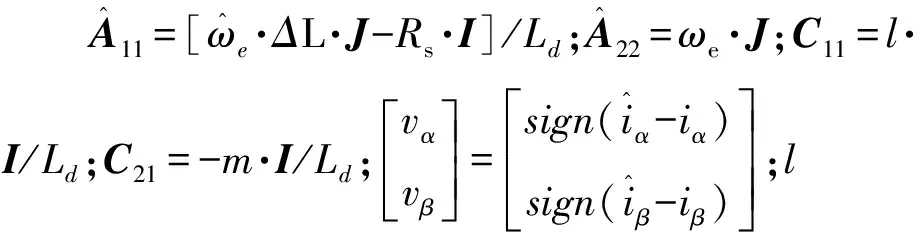
传统的全阶滑模观测器的控制框图如图1所示。

图1 传统全阶滑模观测器结构框图

3 改进型全阶滑模观测器

传统的全阶滑模观测器在达到稳态的过程中,切换函数是不连续的,因此观测出的转子角度和转速存在较大的抖振。将切换函数改成在边界层内连续的sin函数,超出边界层的时候改成间断函数,可减少抖振。同时由于电机在高速时转速很快,即在一个电周期内的路程较远,因此在高速时将切换函数的边界层变厚,使得切换函数的斜率变小。

3.1 变边界层的sin函数

为减少电机抖振,引入变边界层的sin函数,由于sin函数在控制器中运行占用的计算时间大,这里sin函数的实现采用查表法,sin函数的表达式为

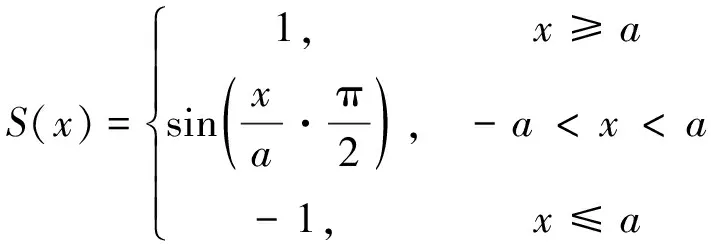
(6)

式中：a为边界层厚度。

a值越大,边界层厚度越厚,其对应的切换函数曲线斜率越小,减少抖振的程度越强。在低速时减小斜率,从而减少抖振。当转速增大时,在电机的一个控制周期内合成矢量走过的路程增大,将切换函数的斜率加大,即边界层厚度减小,可以更好地跟踪观测的反电动势,增加系统的快速性。sin函数的图像如图2所示。

图2 sin函数图像

将滑模的边界层厚度与转速联系起来,同时为了避免电机在低速时边界层厚度过大,影响低速时的性能,将边界层厚度的表达式分为两个阶段,则有：

(7)

式中：a0为转速低时的边界层厚度;a1为比例系数;ωmax为电机的额定转速;ωe为电机的估计转速;ω0为设置边界层的低转速,ω0的取值根据实际系统进行调整,应保证边界层厚度在切换时变化不剧烈,保证整个系统的稳定性。

3.2 自适应滑模增益

由于电机观测的扩展反电动势与电机转速大小成正比例关系,因此在不同转速下选择不同的滑模增益能够使电机更好地跟踪实际的转速和转子位置。为了避免滑模增益在电机转速低时过小,使系统动态性能下降,将滑模增益设置为分段函数,即：

(8)

式中：h0为低转速时的滑模增益;h1为比例系数;ωmax为电机的额定转速;ωe为电机的估计转速;ωk为设置的低转速阈值,同样ωk取值应根据实际系统进行调整,保证滑模增益在切换的时候变化不剧烈。

3.3 改进型全阶滑模稳定性证明

全阶滑模观测器包括电流观测器和扩展反电动势观测器,改进后的观测器表达式为

(9)

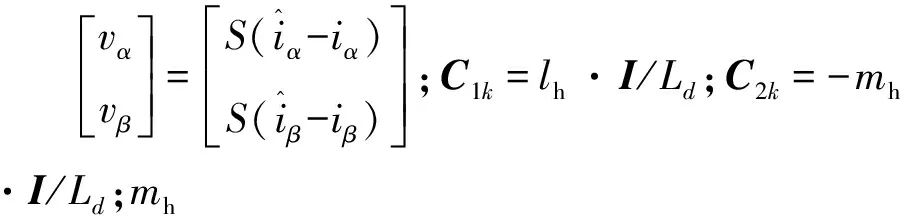
依次对其稳定性进行证明。将式(9)减式(4)可得两个观测器的误差为

(10)

首先对电流观测器进行李雅普诺夫稳定性分析,定义电流的李雅普诺夫函数为

(11)

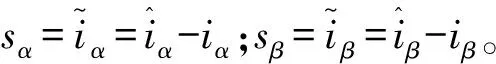
(12)

(13)

将式(13)带入式(10)中的扩展反电势误差方程可得：

(14)

利用拉普拉斯变换对式(14)进行求解可得：

(15)

式中：s为拉普拉斯运算符。

进而求得特征值为

(16)

特征根s1,2为共轭复根,由于电流观测器和扩展反电势观测器的增益都为正,因此特征根都位于s的左半平面,整个系统渐近收敛,扩展反电势的误差会随时间推移逐渐趋近于0。由此可知整个系统是稳定的。

改进后的全阶滑模观测器的结构框图如图3所示。

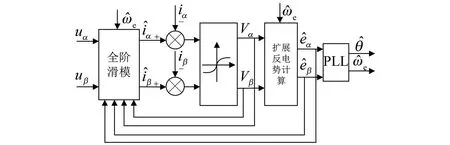
图3 改进后的全阶滑模观测器结构框图

3.4 归一化的PLL转子位置估计

为避免转速对PLL系统带宽产生影响[14],采用反电动势归一化后的PLL进行位置估计。图4为归一化之后的PLL系统框图。

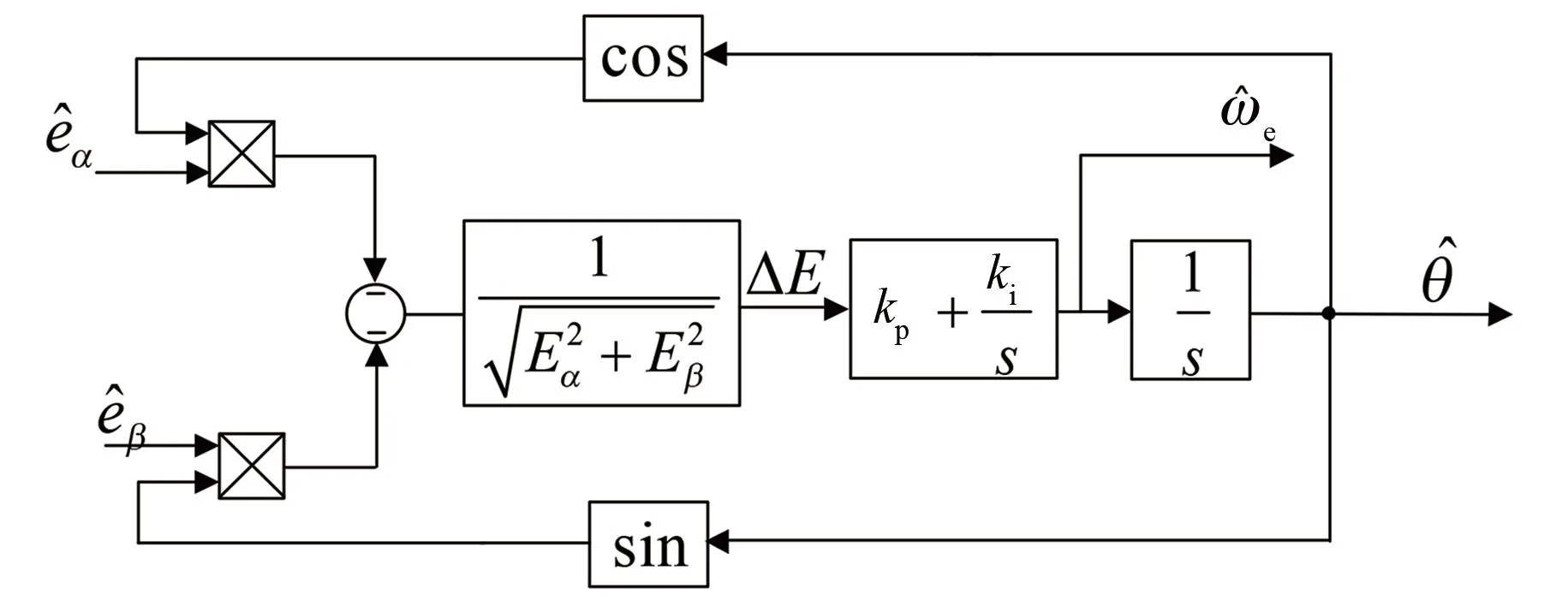
图4 PLL锁相环

将式(2)中的系数设置为k,即：

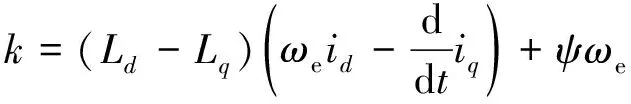
(17)

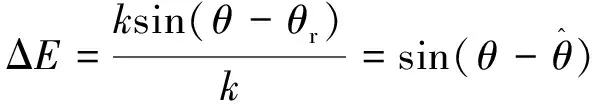
(18)

由式(18)可以看出,归一化之后,反电势误差中不包括转子速度等参数,提高了估计精度。

4 仿真分析

为了验证算法的可行性,在MATLAB/Simulink中搭建模型进行仿真分析。在仿真过程中,选择内置式电机,仿真参数取Ld=6.5 mH,Lq=12.5 mH,电机电阻Rs=0.3 Ω,磁链为0.023 3 Wb,母线电压为48 V,额定转速为1 500 r/min。

由于全阶滑模观测器需要在反电势比较明显时才能进行观测,因此在低速时用I/F强拉起动[15],当转速到达一定数值后,电机反电动势足够大,全阶滑模观测器估测的角度和转速都可以跟踪上实际转速和角度[16];为了使切换顺滑,拉到相应的转速之后,减小iq,当给定角度和估计角度相等的时候,将磁场导向控制(Field-Oriented Control,FOC)算法需要用到的速度和角度切换到观测器输出的角度和速度。整个仿真控制逻辑如图5所示。

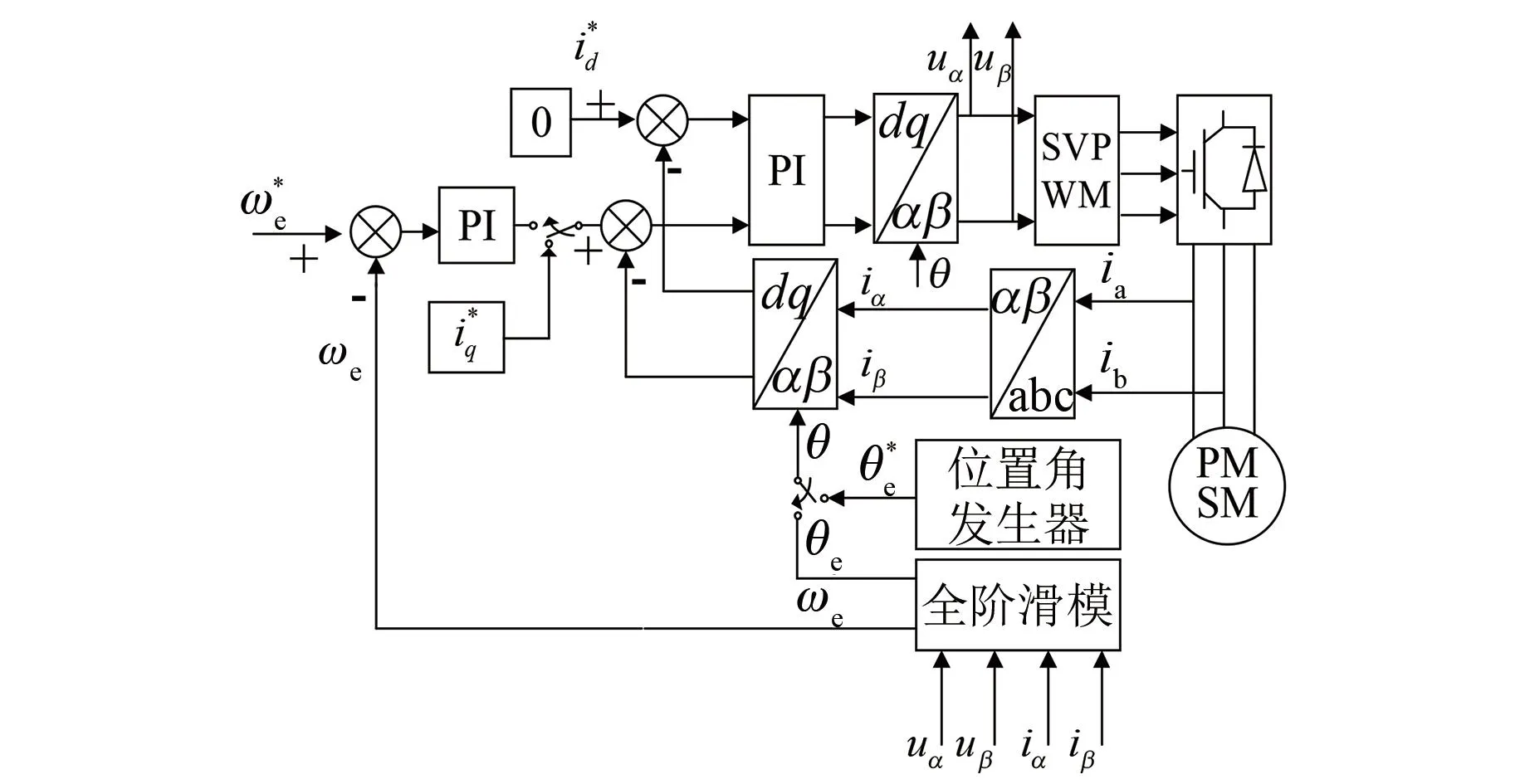
图5 无位置传感器控制系统结构框图

4.1 仿真结果

图6为不同开关函数下全阶滑模观测的电机转速对比,可以看出采用sin函数之后电机转速的波动比传统的sign函数波动小很多,有效地减小了抖振。当电机刚开始转动时,反电势较小,此时观测器失效,当转速跟踪平稳时切换到了全阶滑模观测器上。

图6 不同开关函数下的转速对比

图7和图8为不同切换函数下估测的反电动势。可见,用sign函数估测的反电势抖振严重,改进后的新型sin函数,估测效果好,波形顺滑。

图7 sign函数估测的反电动势

图8 新型sin函数估测的反电动势

图9和图10为达到额定转速后在不同切换函数下的角度误差,可以看出改进后的切换函数角度误差波动小,识别精度高。

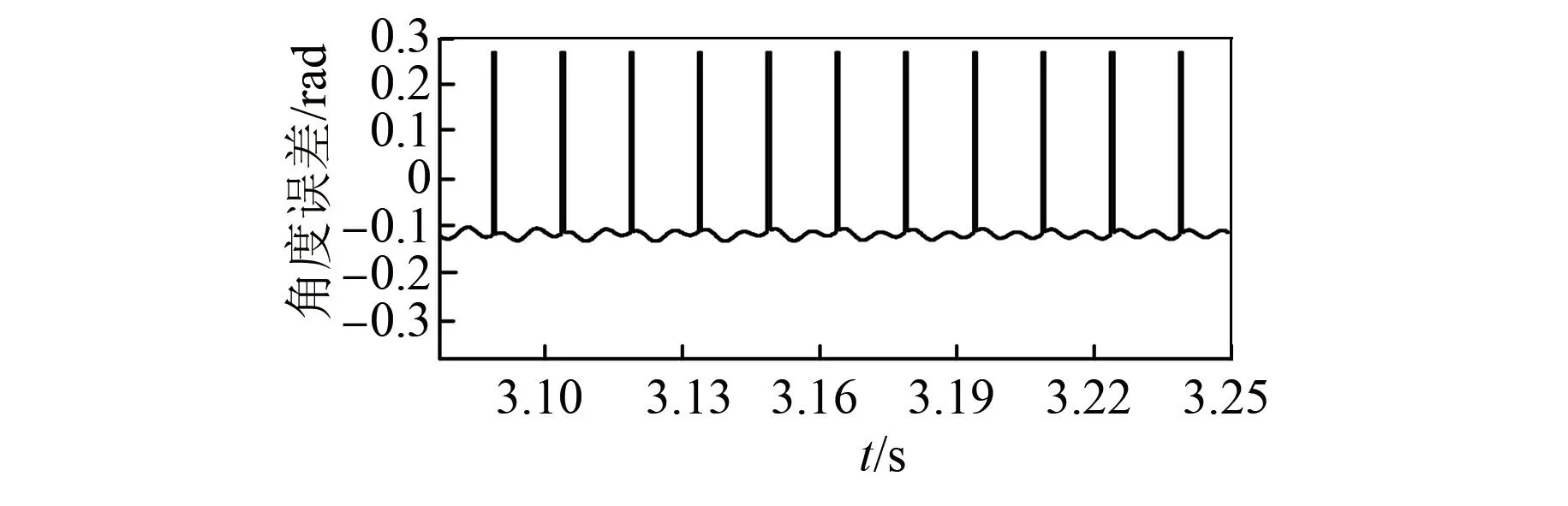
图9 新型sin函数下的角度误差

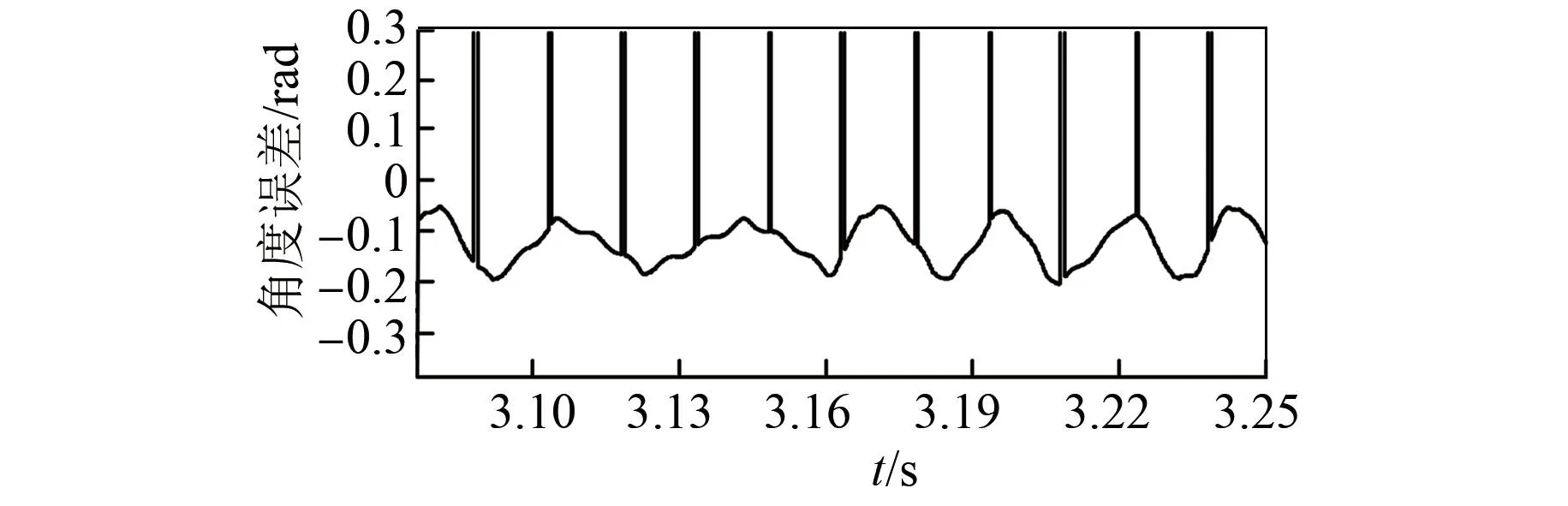
图10 sign函数下的角度误差

5 试验验证

为了验证改进型全阶滑模观测器的性能,搭建了以TC275为主控芯片的硬件验证平台。母线电压采用24 V,利用Vector开发的CANoe软件进行通信;TC275输出相应的脉宽调制(Pulse Width Modulation,PWM)波形,通过控制三相逆变桥导通来控制电机的转动;利用旋变硬解码电路来准确地实时识别电机的转速和转子位置,并与估测出来的转速和转子位置进行比较。整个硬件系统框图如图11所示。

图11 硬件实现平台

5.1 试验分析

首先对比整个系统完整运行的时间,这里sin函数使用查表法[17]。相较于sigmoid函数和tanh函数[18-19],sin函数有效减少了运行时间,减轻了硬件执行的负担。由于使用查表法,避免了执行器进行除法运算,相比于sat函数也减少了运算时间。

表1 程序运行时间

图12和图13为两种切换函数下的转速变化,控制逻辑和仿真中一致。可见变边界层的sin函数估测出来的转速波动小,在低转速时转速跟踪好;而传统的全阶滑模观测器估测出来的转速抖振大,低转速时波动大。根据实际调试,电机在运行过程中ωk和ω0取值选择为300 r/min。

图14和图15为两种切换函数下的角度误差信号。可见sin函数下的角度误差波动小,上下波动在0.04 rad以内,与实际角度相差0.1 rad左右;而传统滑模观测器的角度波动在0.1 rad以内,与实际角度相差0.15 rad左右。综上,改进后的全阶滑模观测器观测精度高且抖振小。

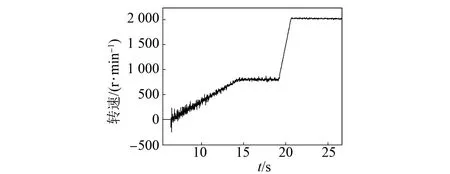
图13 sign函数估测转速

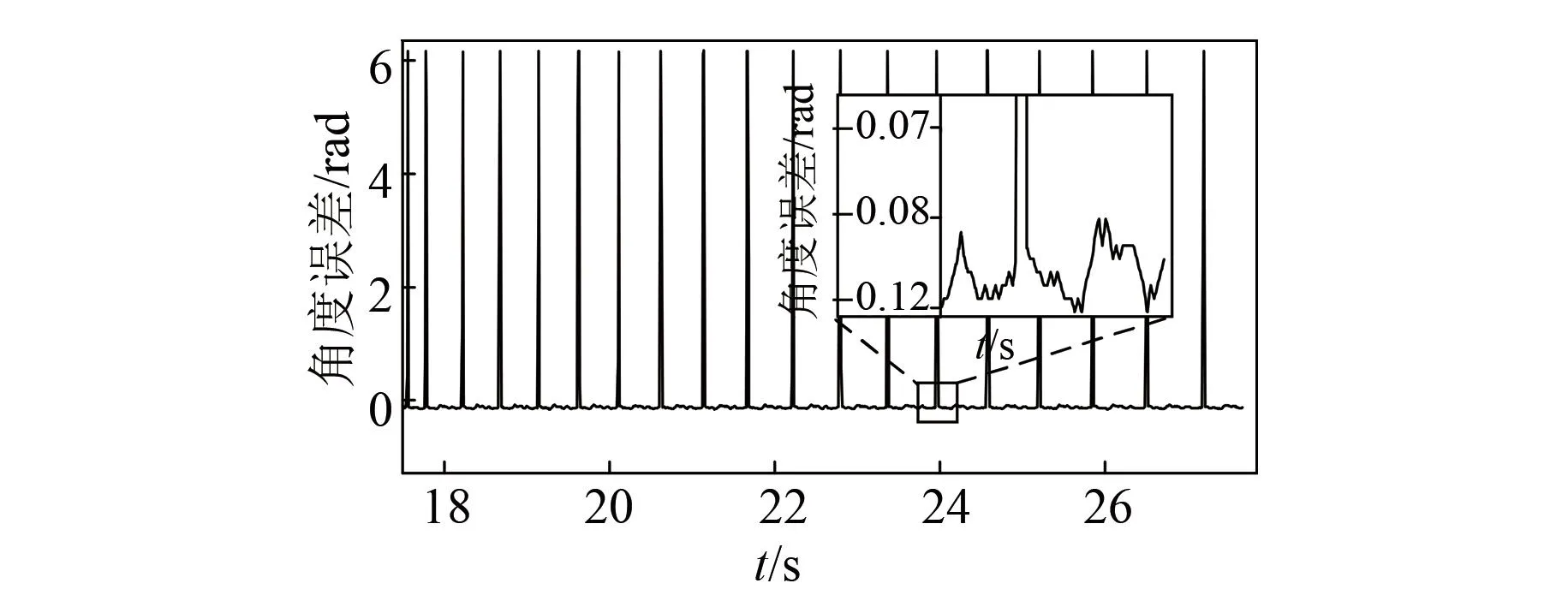
图14 sin函数下的角度误差

图15 sign函数下的角度误差

6 结语

针对传统滑模观测器抖振严重的问题,本文提出了一种变边界层的全阶滑模控制策略。利用新型变边界层的sin函数替换传统的sign切换函数,改进型滑模控制系统有效减小了系统抖振,提高了观测精度。利用归一化锁相环减少无关参数对锁相环的影响,保证了观测精度。sin函数的实现用查表法,有效减少了系统运行时间。仿真和试验结果都证明了改进型滑模观测器的有效性和可行性。

Improved Full Order Sliding Mode Observer Without Sensing Control of Permanent Magnet Synchronous Motors

SONG Jian’guo, LI Zihao*, LIU Xiaozhou

(Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China)

Keywords： permanent magnet synchronous motor (PMSM); full order sliding mode; variable boundary layer; normalized phase-locked loop

Permanent magnet synchronous motor is widely used in many fields such as new energy vehicles, drones and robot control due to the advantages of simple structure, small size, light weight, low loss and high efficiency. In order to save costs and subtract the tedious steps of sensor installation, the sensorless control mode becomes more and more important.

Due to its strong robustness and fast response speed, the sliding mode observer is widely used in the estimation of rotor position and speed of sensorless permanent magnet synchronous motors. However, due to the existence ofbang-bangcontrol function, the traditional full order sliding mode observer has the problems of system chattering and low observation accuracy during operation. Thus, a full order sliding mode control strategy with controllable boundary layer is proposed to solve these problems. The sliding mode gain and the slope of sin function of the motor are linked with the motor speed, so that the full order sliding mode observer can identify more accurately in the estimation process and increase the dynamic performance of the system. Fig.1 shows the block diagram of the improved full order sliding mode observer. A normalized phase-locked loop (PLL) is introduced for speed estimation to avoid the influence of parameter changes on the estimation, which makes the rotor position identification more accurate. The stability of the algorithm is demonstrated using Lyapunov equation. Finally, the reliability and accuracy of the improved full order sliding mode observer sensorless control system are verified through simulation and experiments. Fig.2 shows the block diagram of the sensorless control system. Since the full order sliding mode can only be observed at high speed, the corresponding Angle and speed can be well observed, soI/Fstrong pull is adopted at low speed. Then switch to the full order sliding mode observer, and the sin function uses the table lookup method during the experiment, which greatly reduces the computation time. The simulation and experimental results show that the rotor estimation error of the improved full order sliding mode observer is smaller than that of the traditional full order sliding mode observer, which further increases the application range of sensorless position.

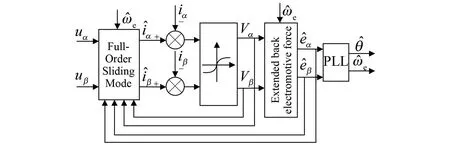
Fig.1 Block diagram of the improved full order sliding mode observer

Fig.2 Block diagram of position sensorless control system