基于比例和改进准谐振控制的MMC环流抑制策略
徐世周, 钟一鸣*, 张梦洁, 裴天一, 姚晶莹
(1.河南师范大学 电子与电气工程学院,河南 新乡 453000;2.中国电建河南工程有限公司,河南 郑州 450000;3.云南师范大学 能源与环境科学学院,云南 昆明 650000)
0 引言
模块化多电平换流器(Modular Multilevel Converter,MMC)作为一种新型电压源型换流器,目前已被广泛应用于高压直流输电系统[1-3]。因MMC能实现高效、可靠地直流输电,其被用于远距离电力输送,如跨国电力传输、海上风电场到陆地的电力传输等。MMC还被广泛应用于分散的可再生能源接入系统以实现能源的高效利用和平稳输出[4-5]。MMC还具有快速响应和精确控制的能力,可用于电力系统的稳定控制和调节[6-7]。此外,由于电动汽车充电需要直流电源,MMC也被用于构建高效、可控的电动汽车充电站,用于新能源车的充电装置[8-9]。然而MMC相间环流中的谐波成分会增大电路中的能量损耗,同时过大的环流会使系统中的电子元件发生过载,缩短系统的寿命[10]。因此如何有效地对环流进行抑制一直都是MMC的研究热点之一[11]。
针对环流抑制问题,文献[12]将三相环流中二次谐波分量与不相等的直流分量分离后单独抑制,采用比例积分控制经二阶广义积分器提取桥臂环流的正、负序二倍频分量,采用准比例谐振控制环流的零序二倍频分量,此策略降低了环流中的二次谐波分量,但需要采用多种控制方法,增加了系统的实现难度和成本。文献[13]结合了自适应陷波器和准比例谐振控制器,采用混合调制方法,有效地抑制环流中的二次谐波分量,降低了桥臂电流畸变程度。文献[14]在准比例谐振控制器(Proportional Resonant Controller,PRC)的基础上提出了一种拓展环流抑制器,结合拓展后的PRC利用环流选择器,对逆变侧负载发生改变时产生的突变环流设定抑制区间进行最优化抑制,拓宽了环流抑制器的应用范围。文献[15]针对传统比例积分(Proportional Intergral,PI)环流控制器存在的问题,设计了MMC分数阶PIλ环流抑制策略,仿真结果表明设计的控制器能够显著的降低环流中二倍频负序分量和总谐波占比。文献[16]基于MMC的平均值模型,提出了一种由两个PI控制器内外两部分组成的环流抑制器,内部控制器抑制共模电压外部控制器抑制二次谐波分量,试验结果表明与传统的PI控制器相比,改进后的环流抑制器更稳定,超调量更小。
上述文献均对环流抑制提出了改进策略,但对除二倍频以外的高次谐波抑制的研究较少。本文首先建立了MMC环流的动态数学模型,构建了一种能够产生反向二倍频分量的比例控制器,该控制器具有结构简单、成本低、响应速度快以及易实现的优点。然后针对更高次的谐波基于已有研究对传统的准谐振控制器进行了改进,在已有对二倍频控制环节的基础上增设了针对四、六倍频的控制环节,设计了一种将比例积分控制与谐振控制相结合的控制器。其中比例积分部分可以实现对环流中的基频成分的无静差跟踪,谐振部分对高倍频的谐波分量进行调节,达到抑制环流效果的同时保证系统的稳定性。最后通过仿真进行验证,仿真结果表明了改进后的控制策略能够进一步地抑制环流,改善波形质量。
1 MMC环流分析
1.1 MMC拓扑结构和工作原理
三相MMC系统的拓扑组成及其子模块的电路拓扑图如图1所示。
MMC的子模块分为全桥和半桥两种结构,本文以半桥结构为主,通过调节子模块中的两个开关管S1、S2的导通和关断可使子模块分别处于闭锁、投入和切除三种工作状态,从而控制整个MMC的运行。
1.2 MMC内环电流解耦策略
由于MMC三相中每一相的组成都是相同的,为了方便分析,以单相MMC的拓扑结构为例进行分析,其等效拓扑图如图2所示。其中:Uuj、Ulj(j=a,b,c三相)分别为上、下桥臂的输出电压;iuj、ilj分别为上、下桥臂的电流;L0为桥臂上的等效电感;R0为桥臂上的等效电阻;Udc和idc分别为MMC直流侧的电压和电流;L1和R1分别为网侧负载的等效电阻和电感;usj和isj分别为负载的电压和电流;icirj为在第j相的内部环流。

图2 单相MMC等效拓扑图
根据图2,由电流定律可得:

(1)
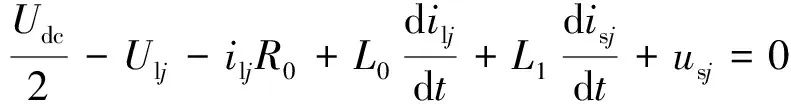
(2)
将式(1)和式(2)相加,可得:

(3)
定义差模电压为
Udiffj=(Uuj-Ulj)/2
(4)
由基尔霍夫的电流定律可得:
iuj-ilj=isj
(5)
结合式(3)~(5)可得:

(6)

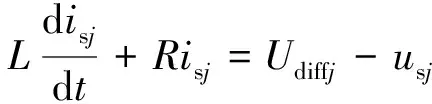
(7)
为了实现易于控制的直流量,通常先对式(7)使用坐标变换,将三相静止坐标系下的正弦交流量转换为两轴同步旋转坐标系(d-q轴)下的直流量。本文采用的是经典的派克坐标变换法。变换矩阵为
C=

(8)
由于闭环系统要与网侧电压的角度保持相同,所以要进行锁相。令θ=ωt,则式(8)变换为

(9)
经过坐标变换后可得:
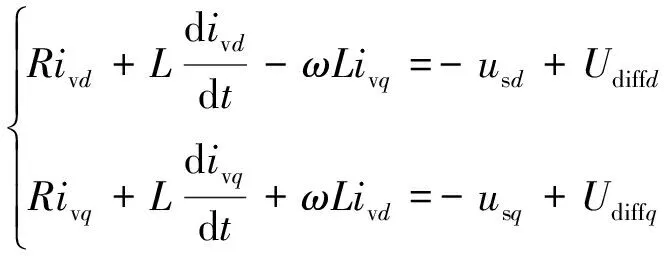
(10)
式中:ivd、ivq分别为isj经过变换后的d、q轴直流量;Udiffd、Udiffq分别为Udiffj经过变换后的d、q轴直流量;usd、usq分别为usj经过变换后的d、q轴直流量;ω为网侧角频率。
式(10)经拉氏变换后为
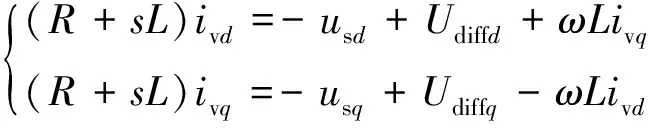
(11)
由式(9)建立d-q坐标系下的动态输入输出模型如图3所示。

图3 d-q坐标系下的内环电流模型
由图(3)所示的模型可知MMC的内环电流中含有耦合量ωL,根据内环电流的数学模型建立内环电流的控制框图,如图4所示。id_ref、iq_ref为电流内环的理想参考值,参考值与实际值作差后经过PI控制器调节,再引入反向的耦合量从而实现电流内环的解耦控制。
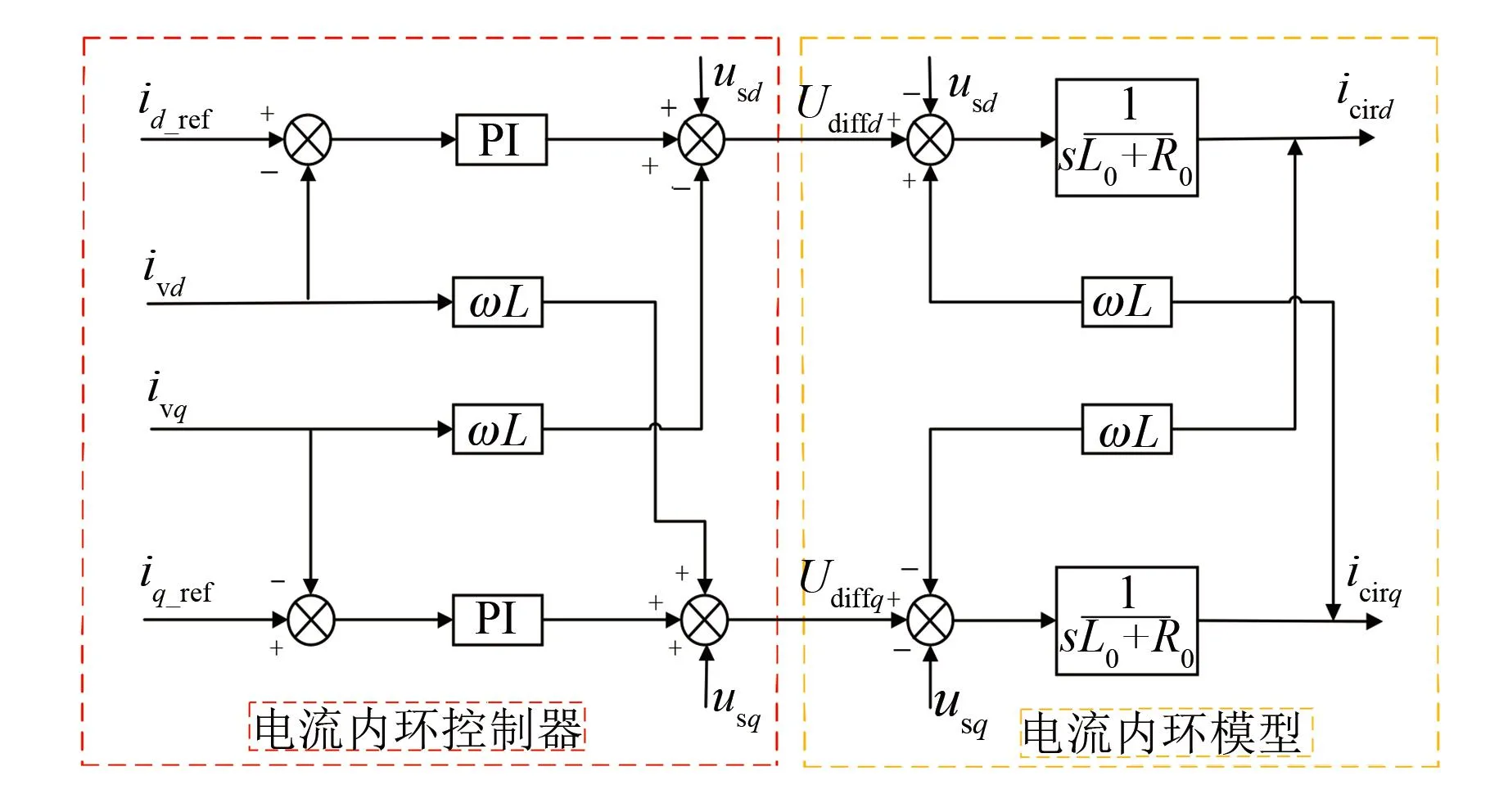
图4 电流内环控制框图
1.3 MMC环流的数学模型
以图2所示的单相MMC拓扑为例建立数学模型。则第j相的上桥臂和下桥臂的电流可分别表示为

(12)
因此第j相的环流可以表示为

(13)
忽略内阻,由电流定律可列方程:
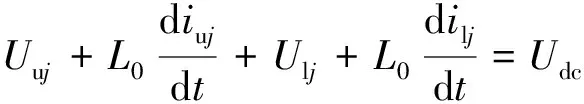
(14)
单相输出参考电压可表示为
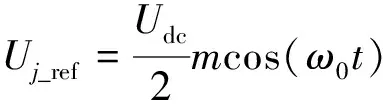
(15)
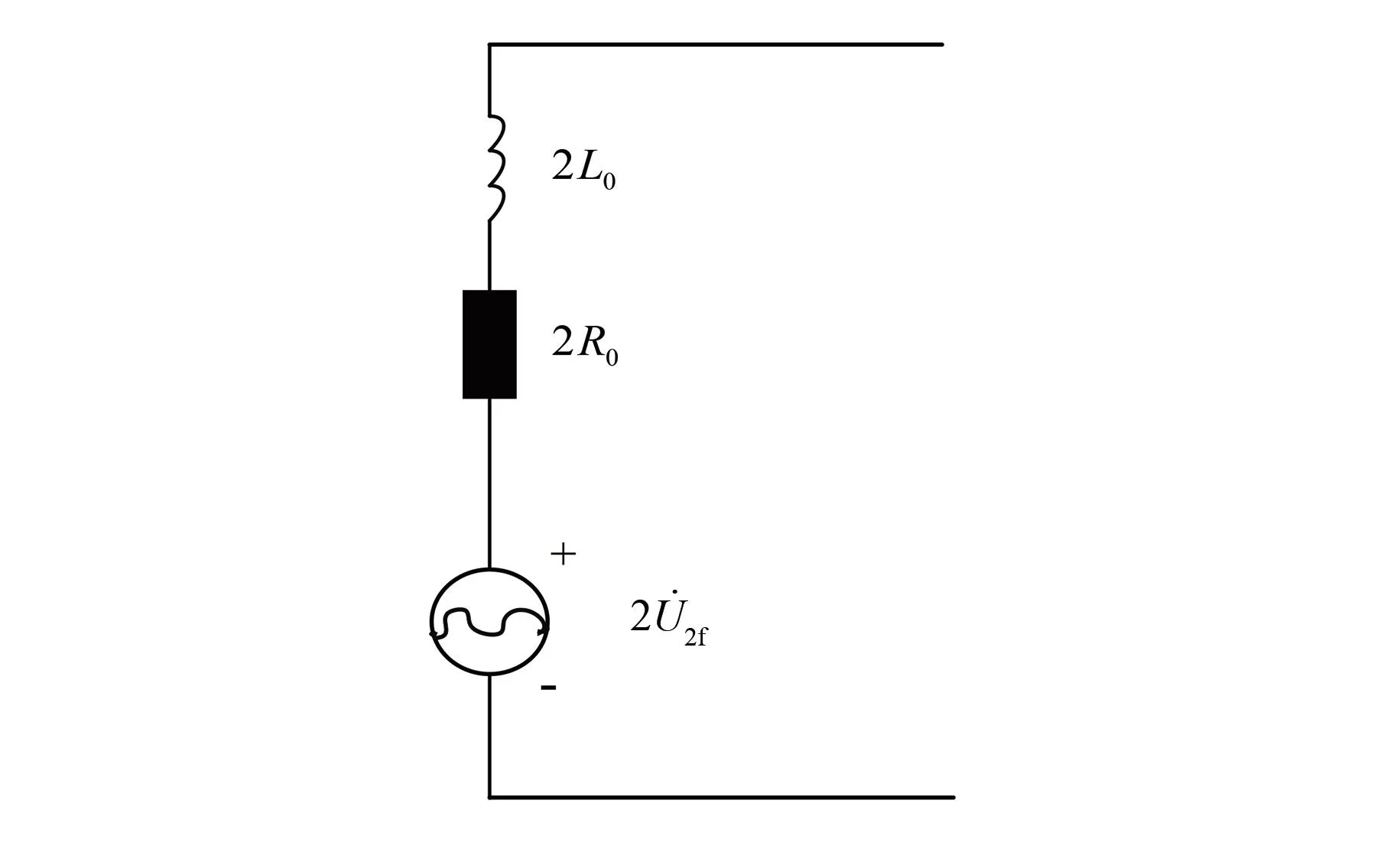
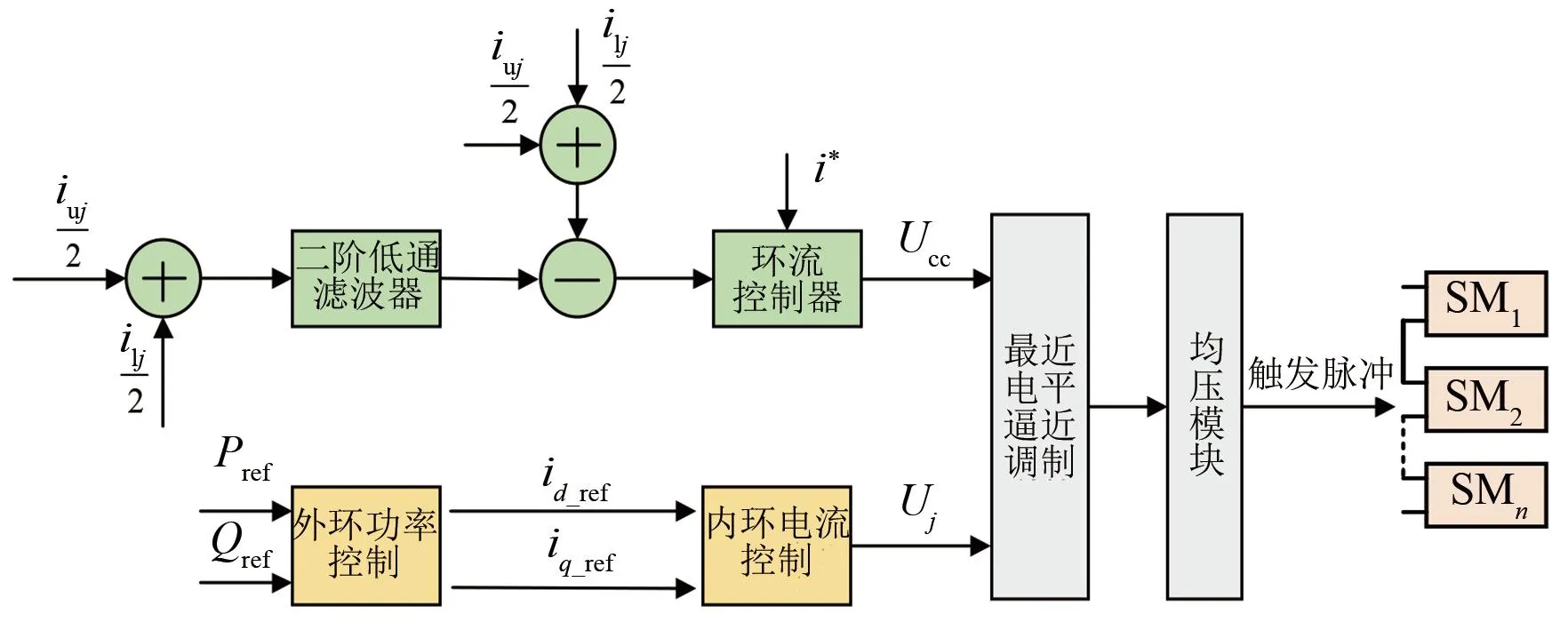
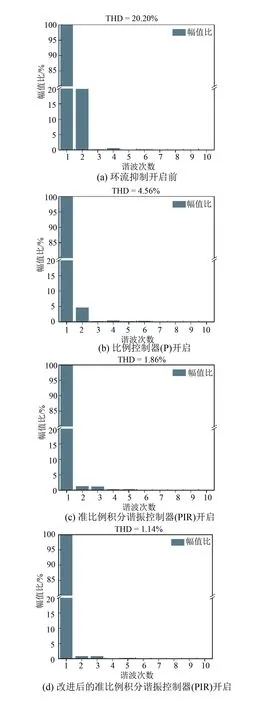
式中:m为调制比,0 设模型的子模块电压为恒定值,桥臂电感上的电压为0,即: (16) 根据基尔霍夫定律,由式(14)~(16)可得第j相的输出电压为 (17) 根据式(14)和式(16),上桥臂和下桥臂的参考电压可表示为 (18) 但在实际运行时子模块的电容电压不是恒定的,即使在理想的情况下,由于交流电的流过也会产生谐波分量。因此,上桥臂电压Uuj和下桥臂电压Ulj实际都是由直流基频分量和交流谐波分量共同组成的,即: 根据式(12)和(14),桥臂电感两端的电压可以表示为 (19) 一般情况下,MMC正常运行时处于投入状态的子模块数量始终占每相子模块总数量的二分之一,因此上桥臂电压和下桥臂电压的和的平均值可近似为Udc,则式(19)可改写为 (20) 由式(20)可以看出上桥臂和下桥臂电压中的谐波分量通过桥臂上的电感向环流中引入了含有谐波成分的电流,同时环流中的谐波成分会再次流入子模块电容。由于桥臂上的电感和子模块电容之间的这种相互作用,即使输入的交流电流为正弦时,环流也会发生畸变产生偶次谐波,在稳态时环流可以表示为[17] (21) 式中:Ik为第k次谐波电流的峰值且k为正偶数。 由此可知,实际的环流中除了含有基频成分以外还含有更高次的谐波成分。在理想情况下,由于MMC子模块电容电压的波动,环流中包含有二、四、六等更高次的偶数次谐波分量。 基于上述分析,环流中除含有基波成分外,必然存在着二倍频及以上的环流,环流产生的本质是由于交流量中的高频成分与线路上的阻抗作用后产生的谐波电流。环流产生的等效模型如图5所示。 图5 MMC环流等效模型 (22) i*=I0+I2f (23) 式中:I0为环流中的基频成分;I2f为环流中的二倍频成分;i*为采集到的环流量。 设计一个比例调节控制器,使用比例控制相当于对线路中的阻抗进行调节产生一个虚拟的阻抗,含有二倍频的电压分量与调节后的阻抗作用后会产生含有反向二倍频分量的环流。再将产生的新环流与原环流叠加,这样就能够将原环流中的二倍频抵消,从而得到新的调制波信号i*′。使用P控制的控制框图如图6所示,ic(s)为经过比例控制器调节后得到的反向二倍频环流分量;i*′为经过调节后的环流值,其表达式为 i*′=i*+ic(s)=I0+I2f+(-I2f)=I0 (24) 通过理论分析可知,比例控制器可以对环流进行抑制,且具有控制结构简单、容易实现以及响应速度快等优点。但控制环节单一,由于MMC子模块电容电压的波动使得环流中依然会存在一定的二、四、六等高频次的谐波分量,因此想要使输出的谐波畸变更小,还应该增加额外的控制环节。 图6 比例控制器控制框图 文献[18]均采用了准谐振控制器对环流进行抑制。谐振控制器属于二阶广义积分器,其在指定的频率处可以实现无穷大的增益效果,因而可以选择性地针对某一频率谐波进行控制。 常规的准比例谐振控制器的传递函数为 (25) 该控制器仅在谐振角频率ωr附近狭窄的频带内有较高的增益。为了提高其抗频率扰动性能,在实际的应用中通常选择针对二倍频环流的准比例谐振控制器,同时加入PI控制器实现对环流中直流成分的无静差跟踪,最终得到环流准比例积分谐振(Proportional Integral Resonant,PIR)控制,其传递函数为 (26) 式中:Kp为比例系数;Ki为积分系数;Kr2为二倍频谐振控制器增益;ωc为截至频率;ωr为谐振角频率。 由环流模型可知环流中除了有二倍频分量,还含有更高频次的谐波分量。因此针对环流中的各次谐波,分别可以在对应的偶次谐波频率处引入谐振控制器,如图7所示。 图7 多偶次谐波谐振控制框图 图7中:Res(2ωr)为针对二倍频设计的谐振控制器;Res(4ωr)为针对四倍频设计的谐振控制器。 (27) 图8 改进后的准PIR控制器结构图 将实际值和给定值的偏差值作为控制器的输入,其中PI环节对环流量中的直流成分可以实现准确地无静差跟踪,谐振控制部分分别对环流中的二、四、六倍频的谐波进行抑制,在保证环流中的基频部分稳定的同时实现对环流中的高频成分的抑制。 为了验证所提策略的可靠性,在MATLAB/SIMLINK平台上搭建了一套23电平的MMC双闭环控制系统。整体控制框图如图9所示。 图9 MMC整体控制框图 环流的提取采用二阶低通滤波器,将原环流与经过滤波后的环流作差即可提取出环流中的谐波分量,再将这些高频谐波与参考值i*(在环流抑制的过程中取i*=0)比较,通过环流控制器进行调节得到参考电压补偿信号Ucc。系统的功率外环和电流内环则采用传统简单可靠的PI控制方式,经过内外环控制后的电压信号与经过环流抑制器抑制后的信号相结合。其中Pref、Qref为功率外环的理想参考值;id_ref、iq_ref为电流内环的理想参考值。最后运用最近电平逼近调制和冒泡排序法对子模块进行均压控制,可生成用来控制子模块开通和关断的触发脉冲,完成对整个MMC系统的控制。模型的主要参数的选取如表1所示。模型中的比例控制器的参数KP=21.4,改进前的针对二倍频抑制的准谐振控制器参数KP=21.4,Ki=47.5,Kr2=415,改进后针对二、四、六高倍频次的准谐振控制器参数KP=21.4,Ki=47.5,Kr2=415,Kr4=205,Kr6=100。 表1 MMC仿真系统参数表 仿真波形以及FFT分析结果如图10和图11所示。环流抑制器开启前波形的FFT分析如图11(a)所示,此时环流的THD值为20.20%,高次谐波的占比较高。环流抑制器开启,三种控制器的输出波形分别为图10(a)、(b)、(c)所示。从图10(a)可见P控制开启后经过0.2 s的调节,环流得到明显抑制,由图11(b)可知此时环流的THD值为4.56%,环流中的二倍频成分被大幅抑制,相比于开启前的THD值下降了77.42%。从图10(b)可见准PIR控制器开启后,经过0.3 s的调节达到稳态,更大程度地抑制了环流,由图11(c)可知此时波形的THD值为1.86%,相比于开启前THD值下降了90.79%。从图10(c)可见改进后的准PIR控制器开启后经过0.3 s的调节,环流的畸变程度同样得了明显的改善,由图11(d)可知此时THD值为1.14%,与控制器开启前相比下降了94.36%。 图10 三种环流抑制器仿真波形 图11 三种策略下的环流波形FFT分析 综上,比例控制器能够快速地达到稳态并对环流起到一定的抑制效果。相比于文献[18]只针对二倍频进行抑制的准谐振控制器,改进后的准比例积分谐振控制器能够分别降低二、四、六倍频的谐波分量,从而优化波形质量。因此比例控制器更适合注重调节时间的应用场合,而改进后的准比例积分谐振控制器更加适合注重波形质量的场合。 为了改善环流谐波的畸变程度,本文设计了一种比例控制器,使其产生反向的谐波分量与原环流中的谐波分量相抵消从而调节环流中的谐波分量。仿真结果表明该控制器经过0.2 s后快速达到稳态,相比于开启前,THD值下降了77.42%。 针对环流中的高频谐波分量,对传统的准谐振控制器进行了改进。经过仿真对比,在调节时间和波动程度基本一致的情况下,改进后的准比例积分谐振控制器相比于改进前,THD值优化了3.56%,对环流抑制的研究具有一定的工程意义。 MMC Circulating Current Suppression Strategy Based on Proportional and Improved Quasi-Resonant Control XU Shizhou1, ZHONG Yiming1*, ZHANG Mengjie1, PEI Tianyi2, YAO Jingying3 (1.Collage of Electronic and Electrical Engineering, He’nan Normal University,Xinxiang 453000, China; 2.Power China He’nan Engineering Co., Ltd., Zhengzhou 450000, China; 3.School of Energy and Environmental Science, Yunnan Normal University, Kunming 650000, China) Keywords: modular multilevel converter (MMC); circulating current suppression; proportional control; resonance control Modular multilevel converter (MMC), as a new type of voltage source type converter, is now widely used in high voltage direct current (HVDC) transmission systems. It enables efficient and reliable DC transmission for long-distance power transmission, such as cross-country power transmission, offshore wind farm-to-land power transmission and so on. However, the modular multilevel converter generates circulating currents flowing between phases due to fluctuations in capacitor voltage, which increases energy loss and adversely affects the insulated gate bipolar transistors (IGBTs) in the sub-modules. In order to suppress the circulating current, the dynamic mathematical model of MMC circulating current is firstly established, and a proportional controller capable of generating inverse two-fold frequency components is constructed, which is simple in structure and has the advantages of low cost, fast response speed and easy to be implemented. Then the conventional quasi-resonant controller is improved for higher harmonics based on the existing literature, and the control link for two-fold frequency has been added on the basis of the control link for four- and six-fold frequencies, and the control link for four- and six-fold frequencies is designed to control the circulating currents. A control strategy combining proportional-integral control and resonance control is designed, in which the proportional-integral part can track the fundamental frequency component of the circulating current without static difference, and the resonance part can regulate the harmonic components of higher frequencies to achieve the effect of suppressing the circulating current and ensure the stability of the system. Finally, the feasibility of the proposed strategy is verified by simulation. The overall control block diagram of the MMC is shown in Fig.1. The simulation results show that the proportional controller can quickly reach the steady state and provide some suppression effect on the circulating current. The conventional quasi-resonant controller is able to further reduce the harmonic components of the second octave, and the improved quasi-resonant controller for higher frequency harmonics is able to reduce the harmonic components of the second, fourth, and sixth octave to optimise the quality of the waveform. Therefore, the proportional controller is more suitable for applications that focus on regulation time, while the improved quasi-resonant controller is more suitable for applications that focus on waveform quality. Fig.1 MMC overall control block diagram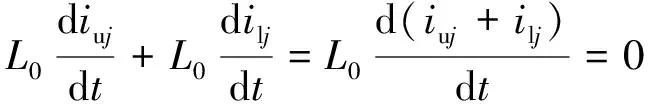



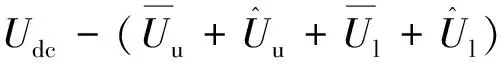
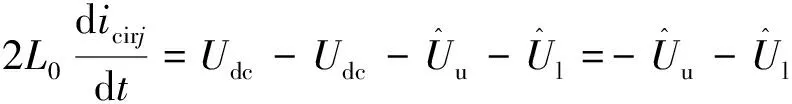
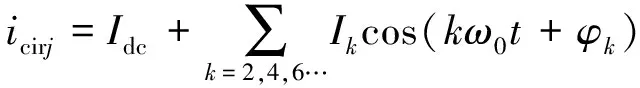
2 环流抑制器设计及控制策略
2.1 基于比例控制的环流抑制器


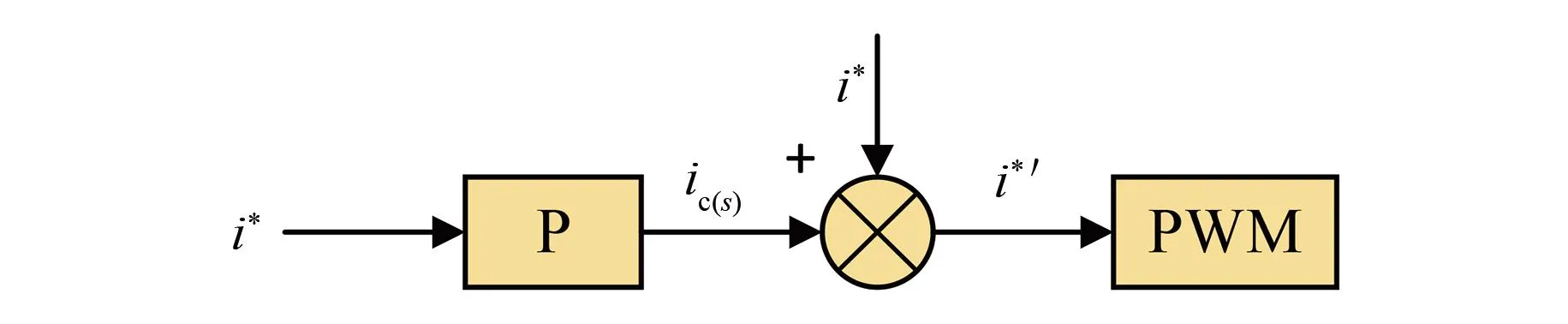
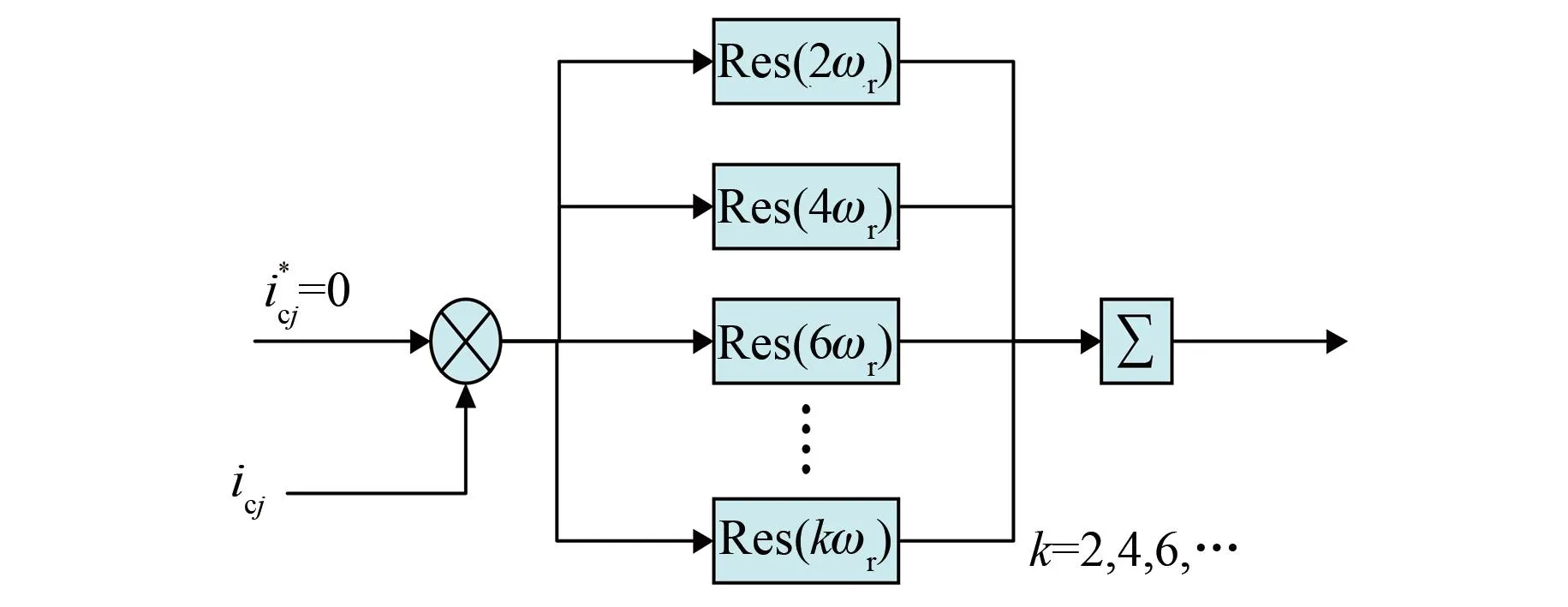
2.2 基于改进型准谐振控制的环流抑制器
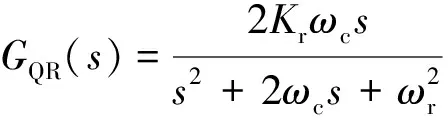
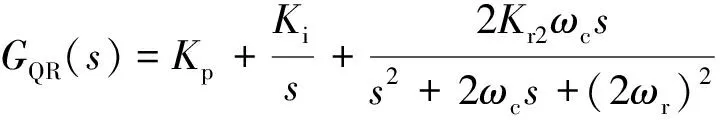
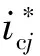

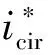

3 仿真分析
3.1 MMC整体控制策略

3.2 结果与分析

4 结语


