单相级联H桥整流器平方电压反馈控制算法
李延帅, 徐传芳, 宋阳阳
(大连交通大学 自动化与电气工程学院,辽宁 大连 116000)
0 引言
电力电子牵引变压器主要应用于高电压、大功率的实际工况,为提高系统转换效率、降低开关器件的压力,无工频级联模块化结构已经成为新的研究热点。单相级联H桥整流器(Cascaded H-Bridge Rectifier,CHBR)作为无工频变压器的前级,不仅要为网侧输入端提供高质量的电流波形,还要对各H桥电压的稳定输出提供保障。深入研究单相CHBR及其控制策略对新一代无工频牵引变压器的发展具有重要意义[1-3]。
针对CHBR的控制要求,文献[4]提供了一种间接电流控制策略,用标准的正弦脉宽调制(Pulse-Width Modulation,PWM)控制取代内部迟滞电流反馈环路,降低了系统的成本,但是开环控制对参数波动敏感,动态响应能力差。相对于间接控制[5-6],直接电流控制以快速电流反馈控制为特征,可以获得高品质的电流响应,主要以比例积分(Proportional-Integral,PI)控制[7-11]与比例谐振(Proportional-Resonance,PR)控制[12-14]最为普遍。但对于单相CHBR来讲,仅对主控制回路进行调制,不足以满足控制需求,在面对负载差异、电网电压幅值、频率畸变等非理想因素时,各H桥输出电压很难快速响应,且会产生较大电压差。因此,文献[15]提出了一种基于模糊PI控制的电压平衡策略,有效减小了CHBR负载投切载时的最大不平衡电压,提高了抗干扰能力,但控制器精度不高,且存在较长延迟时间。文献[16]提出了一种无锁相环电压平衡方法,解决了实际工况中输出电压不平衡的问题,但忽略了耦合项对系统的影响。文献[17]提出了一种以输出电压平方为反馈的电压控制方式,加快了动态响应速度,减小了输出电压在投切载时的误差。
基于上述分析,本文以单相级联H桥整流器为研究对象,从理论和仿真两个角度对单相CHBR的主电路、控制策略以及各H桥输出电压控制进行了研究。基本控制回路采用基于dq前馈解耦的PI控制,使用二阶广义积分算法构建虚拟交流相位,该方法不仅具有良好的谐波抑制能力,而且可以快速提取信号的基波分量,有效提升了网侧电流对电压的追踪能力。另外,通过对功率平衡关系进行推导,发现使用输出电压平方作为控制信号,其参数可随系统的运行状态进行实时调整,在面对扰动时,可有效降低输出电压的最大不平衡电压差,具有很好的动态响应和稳态性能。最后,构建了单相三级联单元的H桥整流器仿真模型,仿真结果验证了所提策略的有效性。
1 主电路
单相级联H桥整流器直流侧输出电压采用串联的连接方式,各单元相互独立,易于扩展,其拓扑结构如图1所示。

图1 单相级联H桥整流器拓扑结构
CHBR模型电路是由交流回路、直流回路以及功率开关管桥路组成。其中交流回路包括网侧输入电感L、电阻Rs;直流回路包括各级联单元直流侧电容Ci和等效负载Ri(i=1,2,…,n);每个级联单元的功率开关管桥路由4个绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor,IGBT)开关器件Si组成。
定义Si的通断状态如式(1)所示:

(1)
式中:Udci为各级联单元直流侧电压;uabi为各级联单元输入侧电压;idci为各单元输出侧负载电流;is为网侧电流。
根据基尔霍夫定律,结合式(1)可得单相级联H桥整流器数学模型为

(2)
式中:us为网侧电压;uab为输入侧电压。
网侧电压、电流关系为
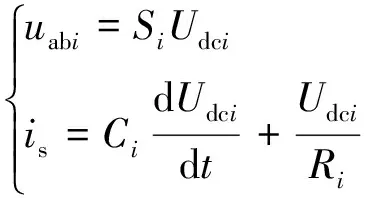
(3)
将式(3)代入式(2),并采用平均运算,使用占空比di代替开关函数Si,即可得平均意义下的数学模型为
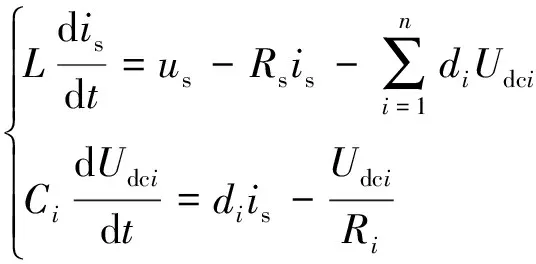
(4)
2 双闭环控制策略
根据单相级联H桥整流器的控制要求,本文采用双闭环的控制策略,控制框图如图2所示。

图2 双闭环控制框图

单相级联H桥整流器网侧电压仅有一个相位,不能通过直接坐标变换实现dq矢量控制,需要构建一个滞后于实际相位“α”为90°的虚拟交流相位“β”。本文采用二阶广义积分(Second-Order Generalized Integrals,SOGI)法构建虚拟交流信号,其结构框图如图3所示。
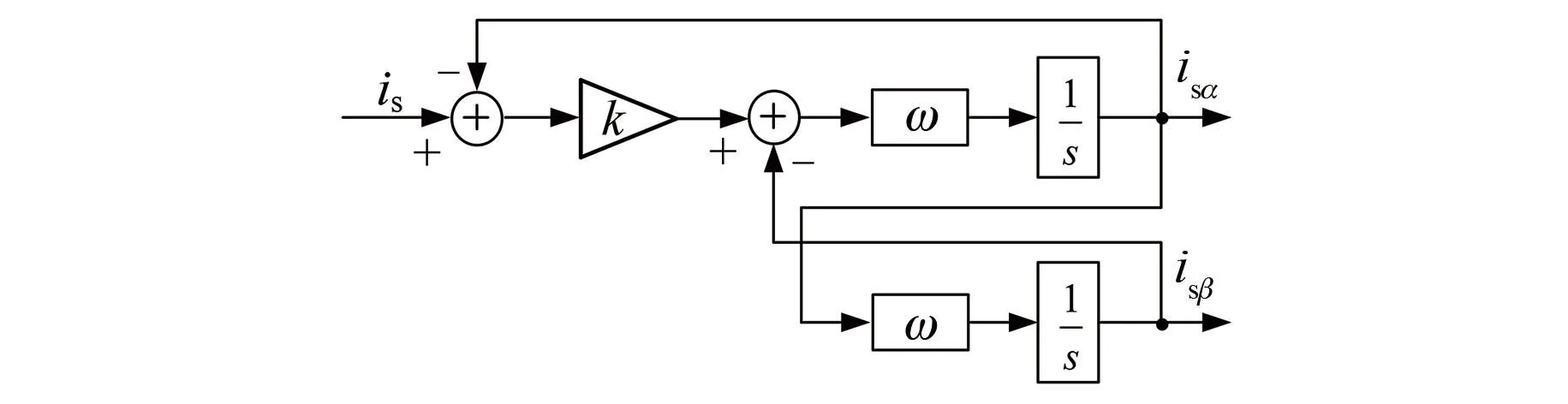
图3 SOGI结构框图
虚拟交流电流分量isβ与网侧电流is之间的传递函数为
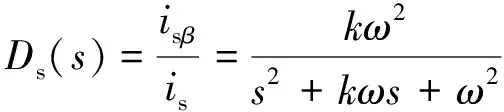
(5)
式中:k为SOGI的控制参数,k越低,系统对谐波噪声抑制效果越明显,但同时也会增加响应时间;ω为网侧电压角频率,构建的交流信号的频率可随系统运行的状态进行实时动态调整。
结合图3所示电路,根据基尔霍夫电压定律可得:
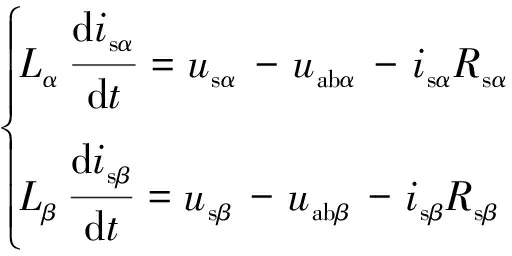
(6)
αβ-dq坐标系之间的变换及其逆变换分别为
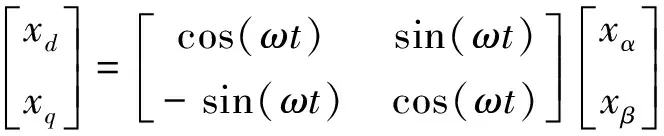
(7)

(8)
将式(7)、(8)代入(6),可得:
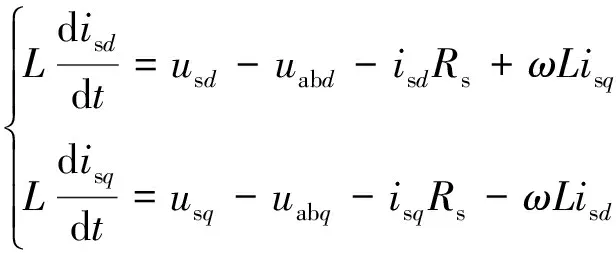
(9)
由式(9)可知,有功和无功电流的动态方程中分别存在耦合项ωLisq和-ωLisd,可以通过dq前馈解耦消除耦合项,实现对其有功分量和无功分量的独立控制。两电流环具有对称性,因此取有功电流isd为例进行电流环的设计,其控制框图如图4所示。

图4 前馈解耦电流内环控制框图
图4中:PI模块的传递函数为WPI(s)=KiP+KiI/s;KPWM为PWM模块等效增益,其开环传递函数为

(10)
式中:KiP和KiI和分别为电流内环控制中PI模块的比例系数和积分系数。
CHBR电流环的总延时时间Td为
Td=3Ts/2
(11)
式中:Ts为系统的采样周期。
系统设计为典型Ⅰ型[18],PI控制器参数方程如式(12)所示:
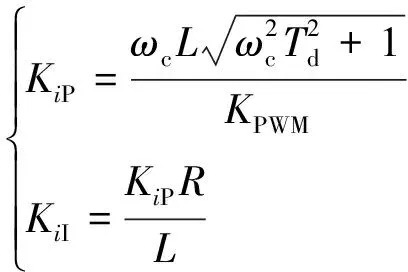
(12)
式中:ωc为系统截止频率。

图5 基于前馈解耦的电压外环控制框图
基于电流内环控制基础,对电压外环进行设计,控制框图如图5所示。其中:h1(s)为电流内环的闭环传递函数;dd为系统公共有功占空比,其表达式为

(13)
在系统保持单位功率运行时,电流内环的带宽远大于外环,h1(s)可近似等效为1[19],则电压外环开环传递函数可表示为
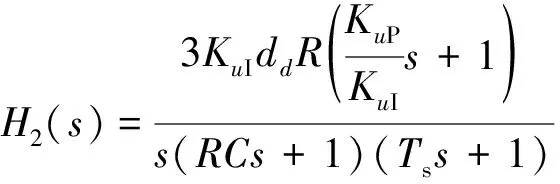
(14)
式中:KuP和KuI分别为电压外环控制中PI模块的比例系数和积分系数。
系统同样采用典型Ⅰ型,PI控制器参数方程为
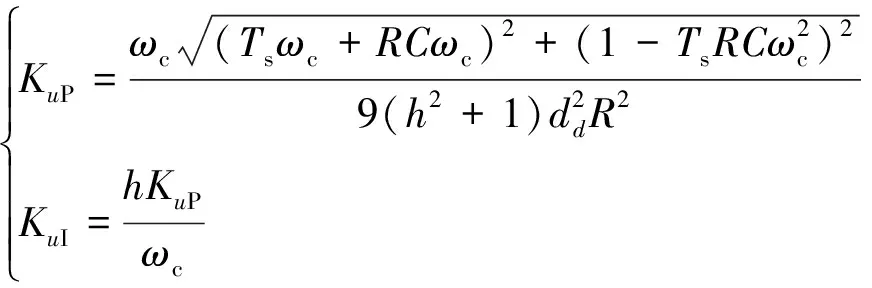
(15)
但这种直接将调节器作用在dq坐标系的设计方式忽略了虚拟正交分量解耦项对系统性能的影响,需要额外设计电压平衡策略进行处理。
3 电压平衡控制策略
为解决CHBR直流侧电容电压不平衡的问题,文献[20]提出了一种传统电压平衡控制器模型,其控制策略框图如图6所示。
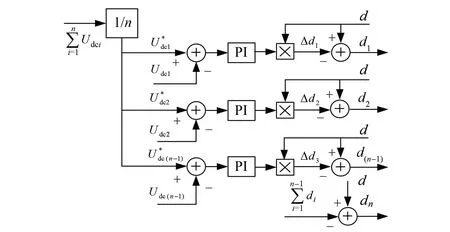
图6 传统电压平衡控制策略框图
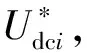
di=d+Δdi
(16)
式中:d为公共占空比;di和Δdi分别为每个级联单元的占空比和占空比增量。
但整流器的瞬时输入功率具有二倍频脉动的特性,输出电压含有纹波信号,在系统进行大范围投切载时,直流侧会产生较大的电压差,影响系统稳定性。为此,本文基于传统电压平衡控制策略进行改进,提出了一种更符合实际模型的平方电压反馈控制策略,如图7所示。

图7 平方电压反馈控制策略框图
通过对模型功率平衡关系式的定义,可得到交流侧的瞬时功率Pabj为
Pabj=uabis
(17)
直流侧的瞬时功率Pdci为
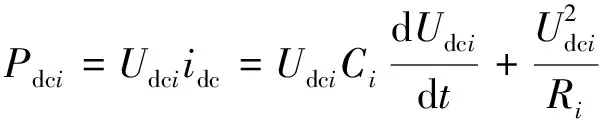
(18)
忽略H桥开关器件的功率损耗,根据功率守恒定律,各模块直流侧和交流侧的功率满足:
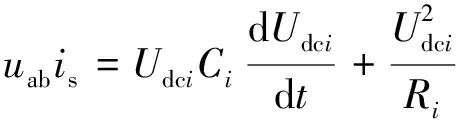
(19)
对式(19)进行变换后可得:

(20)
结合图7的控制结构及式(20),取电压的偏差信号为
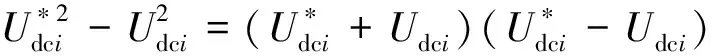
(21)

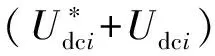
另外,也需考虑电压平衡控制器对dq解耦控制器所造成的影响。经过αβ-dq坐标系变换后,CHBR在dq坐标系中的动态方程为
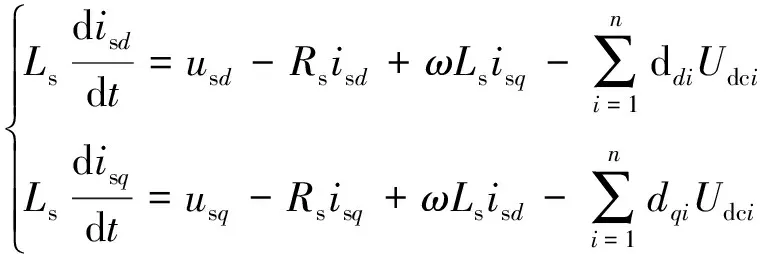
(22)
设d、q轴引入电压平衡控制后的耦合项分别为A1、A2,其表达式为
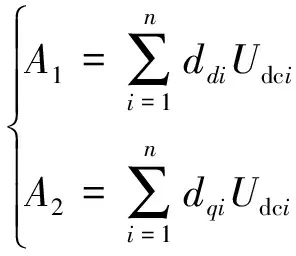
(23)
A1、A2越接近0,电压平衡控制器对基本dq解耦控制器所造成的影响越小。且由于系统保持单位功率因数工况下运行,Δdqi=0,能够实现无功功率平衡控制。因此只需对有功占空比进行修正,对其第N个模块的占空比进行开环调节,如式(24)所示:
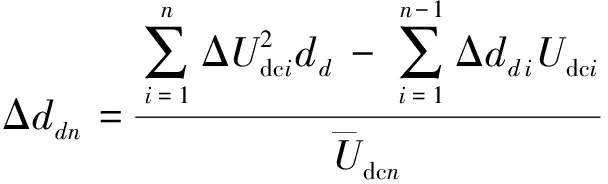
(24)
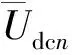
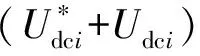
4 仿真分析
本文基于MATLAB/Simulink软件构建了三级联模块的CHBR仿真模型,仿真参数如表1所示。

表1 仿真参数表
4.1 与传统电压平衡策略的对比
默认设置电压平衡模块在0.6 s前不作用,在0.5 s时,设置电阻R1不变,将R2和R3分别设置为8.5 Ω和7 Ω。图8(a)和8(b)分别为采用传统电压平衡算法和平方反馈电压算法的直流侧电压波形。

图8 两种电压平衡策略负载变化时仿真波形
由图8可知,在0.5 s负载发生改变时,各级联单元产生了压差;0.6 s时,电压平衡模块起动,两种策略下输出电压经波动后均趋于平衡,采用平方反馈电压控制算法的系统在负载切换时产生电压差更小。在1 s时,将R1、R2和R3分别设置为8.5 Ω、7 Ω和5.5 Ω,可以观察到采用平方反馈电压控制的系统在负载切载时,产生的波形压差较小。而且在整个仿真过程中,平方反馈电压控制系统电压波动更平缓,具有更好的静态特性。综上可得,相较于传统电压平衡方法,平方反馈电压控制算法在负载投切载时具有更好的动态和稳态性能。
4.2 系统负载不平衡时的仿真验证
在0.6 s时,设置电阻R1不变,将R2和R3分别设置为9 Ω和8 Ω;在1.1 s时,设置R2和R3分别为11.5 Ω和13 Ω;在1.6 s时,R1、R2和R3均恢复为10 Ω。负载投切载时仿真波形如图9所示。
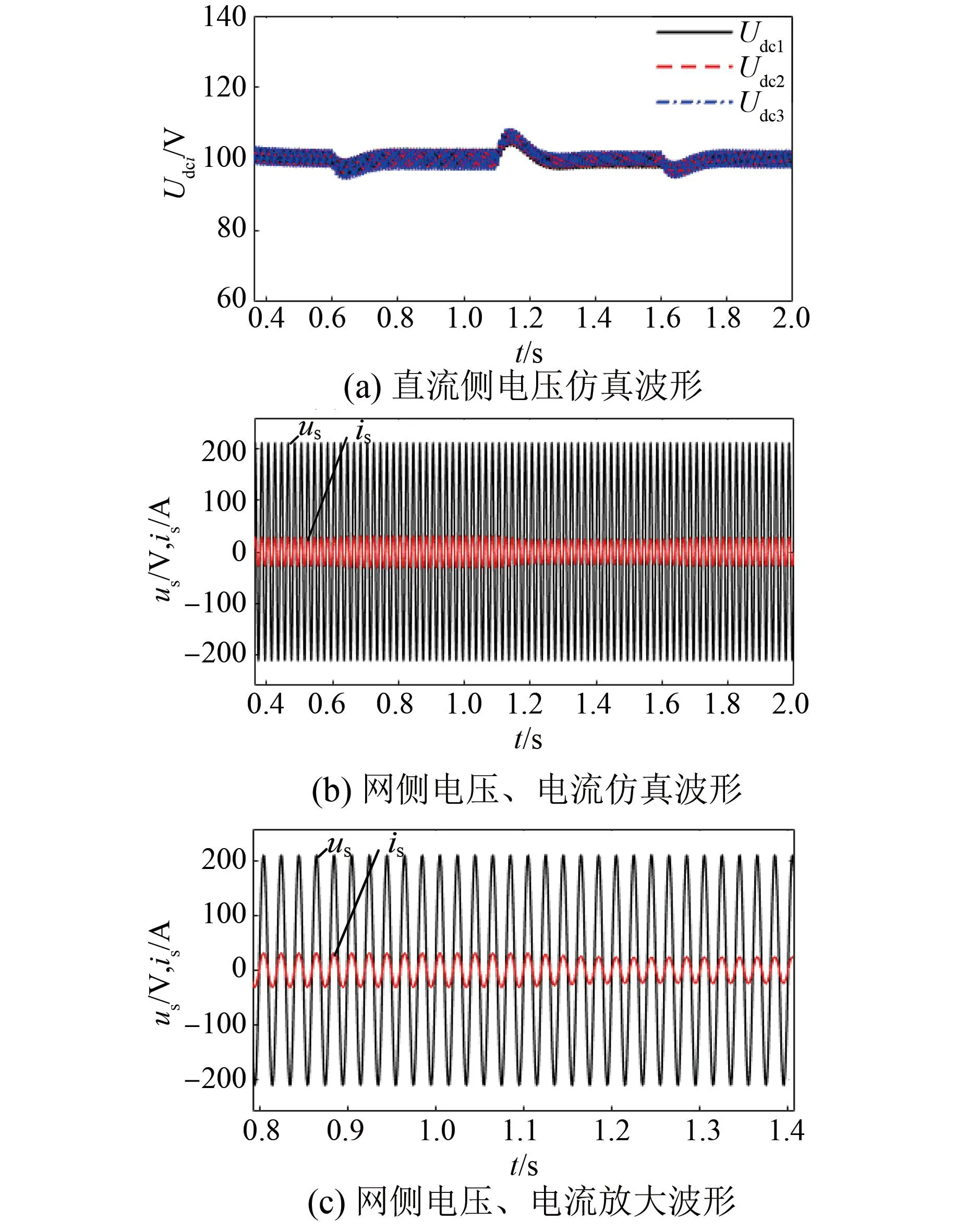
图9 负载投切载时仿真波形
虽然负载不平衡,但从图9(a)和(b)中可以看出,系统直流侧电压面对扰动时,具有较快的响应速度和抗扰能力;网侧电压、电流波形同相位,实现了单位因数控制。由图9(c)所示的网侧波形放大图可见网侧电压、电流在切换时也能平滑过渡,保持同频同相位,无畸变信号。仿真结果表明该方法能很好地应对负载不平衡的现象。
4.3 系统工作在非理想电网时的仿真验证
设置网侧电压在0.6 s时幅值提升20%,升高至250 V;在1.1 s时,电压频率改变至60 Hz;在1.6 s时,电压幅值和频率均恢复正常,仿真波形如图10所示。

图10 电压幅值、频率发生改变时仿真波形
由图10可知,在网侧电压幅值、相位发生变化时,直流侧电压在经过短暂扰动后,能够迅速恢复平衡;网侧电流能始终追踪电压相位变化,在系统切换时也能够平稳过渡。进一步对网侧波形进行放大,如图10(c)所示,可见在0.6 s时,电压、电流幅值发生改变,但仍保持同频同相位,正弦度良好。仿真结果表明在电压幅值、频率改变时,该方法能够有效减小电压平衡响应时间,维持直流侧电压恒定,保持系统单位功率运转。
5 结语
本文以单相级联H桥整流器为研究对象,主控制模块采用电流电压双闭环策略,在基于dq前馈解耦的PI控制的方法上,加入二阶广义积分算法,构建虚拟交流分量。电压平衡模块采用直流侧电压平方作为控制信号,并针对有功占空比对解耦项设置了开环调节。通过仿真,验证了所提策略的有效性,得到如下结论:
(1) 相较于传统电压平衡控制算法,在负载投切载时,平方电压反馈控制算法在平衡直流侧电压。降低扰动时的电压差以及缩短平衡恢复时间方面具有显著的优越性。
(2) 在电网幅值、频率波动,或负载不平衡时,所提策略具有良好的动态性能。一方面表现为网侧输入端能够保持单位功率运转,在切换时电压、电流也能完成平滑过渡;另一方面,各单元直流电压面对扰动具有极快的响应速度,产生的波动电压差较小,降低了在实际工况下的运行风险。
Square Voltage Feedback Control Algorithm for Single-Phase Cascaded H-Bridge Rectifier
LI Yanshuai, XU Chuanfang*, SONG Yangyang
(School of Automation and Electrical Engineering, Dalian Jiaotong University, Dalian 116000, China)
Keywords: single-phase cascade H-bridge rectifier; double closed-loop; square voltage feedback control;dqfeed-forward decoupling control
Power electronic traction transformer is mainly used in high voltage, high power actual working conditions. In order to improve the conversion efficiency of the system and reduce the pressure of switching devices, the non-power frequency cascade modular structure has become a new research hotspot. As the precursor stage of the non-power frequency transformer, the single-phase cascaded H-bridge rectifier (CHBR) not only has to provide a high-quality current waveform for the grid-side input, but also has to provide a guarantee for the stabilized output of each H-bridge voltage. The in-depth study of CHBR is of great significance to the development of a new generation of non-power frequency traction transformers.
In this paper, the single-phase cascaded H-bridge rectifier is taken as the research object, the main circuit, control strategy and output voltage control of each H-bridge of the single-phase CHBR are investigated from from both theoretical and simulation perspectives. The basic control loop adopts PI control based ondqfeed-forward decoupling, and uses the second-order generalized integral algorithm to construct the virtual AC phase, which not only has good harmonic suppression capability, but also can quickly extract the fundamental component of the signal, effectively improving the tracking capability of grid-side current to voltage. In addition, through the derivation of the power balance relationship, the output voltage squared is used as the control signal, and its parameters can be adjusted in real time with the operating state of the system, which effectively reduces the maximum unbalanced voltage difference of the output voltage in the face of disturbance, and has a very good dynamic response and steady-state performance. Finally, a simulation model of the H-bridge rectifier with single-phase three-cascade unit is constructed, and the simulation results verify the effectiveness of the proposed strategy.
The single-phase cascaded H-bridge rectifier model is shown in Fig.1, the main control module adopts the current and voltage double closed-loop strategy, and adds a second-order generalized integral algorithm to construct a virtual AC component on the PI control method based on feed-forward decoupling. The voltage balancing module redefines the power balance relationship of the system, uses the DC side voltage square as the control signal, and sets up open-loop regulation for the decoupling term of the active duty cycle. The effectiveness of the method is verified by simulation.

Fig.1 CHBR control block diagram

