STATCOM并网侧LCL谐波抑制器新设计方法
宋亮
(南阳理工学院数理学院,河南南阳473004)
无功补偿装置中PWM变流器的开关频率一般为2~15 kHz,开关引起的谐波会对挂在电网上的对EMI敏感的设备有干扰。
为了降低变流器引起的电流谐波,需要大的滤波电感。但对于容量比较大的PWM变流器而言,电感既大又贵,而且系统的动态响应受到影响,影响到直流母线电压的利用率[1-3]。
应用于逆变器的输出谐波抑制器的类型一般有L型和LCL型。传统的STATCOM装置一般通过单个电抗器L并联接入系统,仅依靠单个连接电感需要很大的电感量才能获得满意的谐波抑制效果,这将大大增加装置的成本,过大的电感还会影响装置的动态性能。1995 年M.Lindgren 和J.Svensson 首先提出用1个三阶LCL型谐波抑制器代替原有L 型谐波抑制器的思路[4],随着研究的深入,LCL型谐波抑制器在并网逆变器中得到了深入研究和广泛应用。
本文主要对静止同步补偿器LCL 型谐波抑制器的数学模型进行详细分析,并详细提出了LCL型谐波抑制器新设计方法的思路和步骤,而后在仿真实例中按照上述步骤来设计LCL 型谐波抑制器的各个参数,同时也对LCL型谐波抑制器和L型谐波抑制器的谐波抑制效果进行了对比研究,并在PSIM中搭建了基于上述两种谐波抑制器下的系统仿真模型并进行仿真实验对比分析,最后通过实验平台验证了理论分析的正确性。
1 LCL型谐波抑制器参数取值新方法分析
LCL 谐波抑制器的目标是降低输入电网的高次谐波,但如果谐波抑制器设计得不好,不但不会对高次谐波进行衰减,反而会增加电流的畸变。变换器产生的电流谐波会引起电感和谐波抑制器谐振。因此,电感值的选取必须考虑电流的波动情况,谐波抑制器应有阻尼以避免谐振的产生。
LCL 谐波抑制器参数的选择主要由输入功率的定额、电网的频率和开关频率来确定。
因此,谐波抑制器参数的阻抗基值Zb为

式中:En为线电压的有效值;Pn为视在功率。

式中:ω 为市电的频率;Cb为滤波电容的基值。
谐振角频率与开关角频率的关系可以表示为

式中:ωres为谐振角频率;ωsw为开关角频率;k为表征二者之间相距远近的1个系数。
单相LCL 谐波抑制器的等效电路图如图1所示。

图1 LCL谐波抑制器的示意图及传递函数框图Fig.1 Schematic and transfer function block diagram of LCL type harmonic current suppressor
由传递函数框图可以看出:

根据式(4)可以得到v与ig之间的关系:

由上式可见,电感电容取不同的值时,传递函数的形式不变,所以电感电容的选值很有讲究。

当s→0时,式(7)可以近似为

式(8)表明了流向电网电流与逆变器输出电流之间的关系。
由式(4)的第3 式去掉电网电压后代入第2式得到:

进而得到:
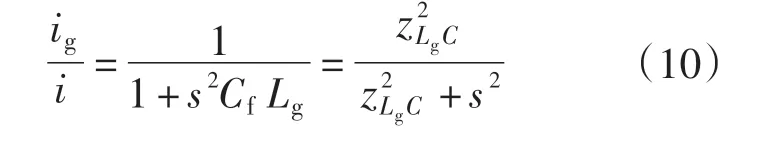
而由式(6)和式(8)相除得到近似表达式为

把式(6)、式(8)、式(11)中的s换成jωsw就得到在开关角频率下各量的频域的幅值关系(不包括相位关系):

2 LCL型谐波抑制器新方法的设计步骤
有很多文献都讲述了LCL 的参数设计[5-9],一般对于电感参数的设计都是进行总电感L+Lg的设计,主要是参考了L型谐波抑制器的设计方法,如下式所示:
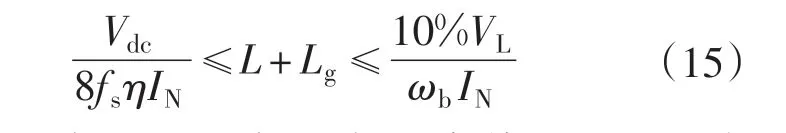
对于电容Cf的设计,一般要求其吸收的基波无功功率不大于系统额定功率的5%。因此可得:

式中:k 为比例系数,满足k<5%;VS为电网相电压有效值。
对于网侧电感Lg其对高频谐波电流呈现高阻抗,大部分谐波电流从电容支路流通,根据文献[9]所述,可以按照要求通过计算即可得到Lg的取值,再根据式(15)计算所得的总电感取值范围,即可确定L的取值范围。
对于阻尼电阻R,一般取值为谐振点容抗的1/3,即:

式中:fres为滤波器的谐振频率。
上述方法是工程经验方法,不利于我们对于LCL谐波抑制器的深入理解和调整设计,下面本文介绍一种程序设计的方法对LCL 谐波抑制器进行参数设计,设计步骤如下:
1)根据变换器端输出电流或输入电流的波动量的上限值来选择变换器侧电感L 的下限值,可以根据式(13)所给出的变换器输出电压与电感电流的传递函数来计算。
电网侧的电感Lg与变换器侧的电感成比例:

式中:r为1个系数。
2)滤波电容Cf值的选择是由在额定功率时所能允许的功率因数决定的,即变换器和谐波抑制器所允许吸收的无功的上限所决定的。

其中,x是在额定工作状态下吸收无功的百分比,即一般状态下吸收的无功与额定工作状态下吸收的无功的比例。
3)选择流向电网的电流波动的范围,从而求出r,也就得到了Lg。
将式(18)、式(19)代入式(14)中可得:

实际上根据式(10)会推出不一样的结果,而这个结果却是精确的结果,如下式所示:

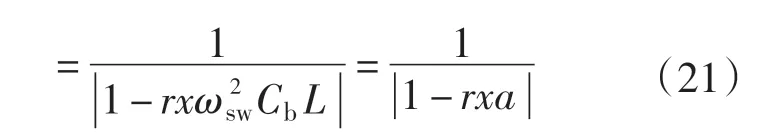
在利用式(20)或式(21)进行计算r之前,必须对这2个电流的衰减比留有裕量,即2个电感的阻抗之和不能超过10%的阻抗基值。如果超过了,则可以调整这个衰减比或者说调整电容的值。
4)校验谐振频率:

令ωres=kωsw,于是有:

谐振频率应保证在10 倍的工频和一半的开关频率之间,如果不能满足这个条件,就要重复上面的步骤2)和步骤3),使之符合要求。
5)根据被动阻尼的限制条件来设计阻尼电阻。在谐振频率点,LCL谐波抑制器的阻抗为0,阻尼的目的就是插入1 个阻抗,使得在这一个频率时,LCL阻抗不为零,以避免振荡。因此,阻尼的值设定为与电容在谐振点的阻抗值相同的数量级。
如果LCL谐波抑制器的衰减不够,设计过程返回到步骤3),重新设计,如果结果还是不行,则返回步骤2),并且选择一个比较大的无功分量。
6)校验谐波抑制器在其它负载和开关频率下的性能。
上述程序过程,可以通过C 语言编程进行迭代计算,将符合上述要求的取值都挑选出来,或者通过EXCEL表格计算列出所有符合要求的取值,本文中是通过Matlab 中的编程得出关系图,选取图中符合条件的LCL 电流谐波抑制器各参数值。
3 LCL型谐波抑制器仿真参数计算并与L型谐波抑制器的性能比较
线电压为380 V,总功率为10 kvar,开关频率为20 kHz和10 kHz两种情况来考虑,根据这些原始条件来设计。通过下面计算可以得到:

1)选择2.7%的阻抗基值作为变换器侧电感的感抗,这样可以获得10%的电流波动。LC部分的作用是将这10%的电流波动衰减为2%。通过计算得到变换器侧电感为1.24 mH 的电感值,这里取1.28 mH。
2)最大的电容值为220×5%=11μF,选10 μF的电容,也可以先取一半。
3)通过选择电流的衰减比和谐振频率来选择2 个电感之间的比例。根据式(17)、式(18)可以得到如图2和图3所示的波形。谐振频率与开关频率无关,但谐振频率要高于控制系统的带宽,也就是谐振发生在控制带宽以内,可以通过控制加以抑制,但是一般采用开关频率1/4~1/2左右。本文决定选在4~5 kHz 之间,以便开关频率可以选在10 kHz和20 kHz。

图2 电流衰减比与Lg/L之间的关系Fig.2 The relationship diagram between current attenuation ratio and Lg/L
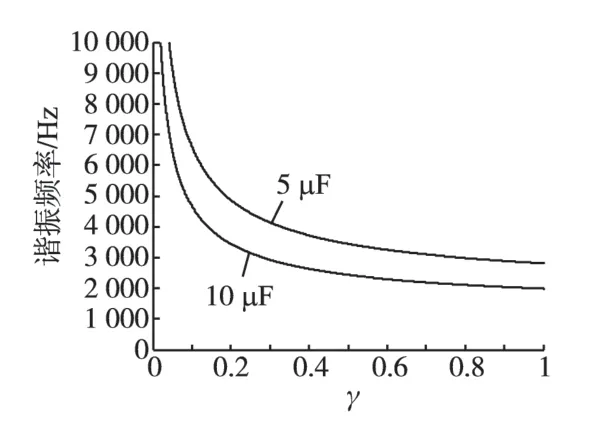
图3 谐振频率与r之间的关系图Fig.3 The relationship diagram between the resonant frequency and r
根据图3,可以看出当电容为5 μF时,如果r=0.2,谐振频率为4~5 kHz 之间。当电容为10 μF时,如果r=0.1,谐振频率为4~5 kHz之间。选择谐振频率在10 倍的工频和1/2 的开关频率之间,主要是为了防止谐振对地工频量的控制产生影响。
由图2a 可以看出,当开关频率为20 kHz 时,r=0.1 或更大时,2 个电流的衰减比很理想,在大约8 倍以上。由图2b 可以看出,当开关频率为10 kHz 时,r=0.2(C=10 μF)和r=0.4(C=5 μF)时才能达到8倍左右的衰减率。此时,谐振频率为3~4 kHz之间,对于10 kHz的开关频率,这也是可以满足要求的。
综上所述,设计电感主要有以下几个:一是变换器侧电感1.28 mH;二是网侧电感,可以选择128 μH,256 μH,512 μH。电容值分别选择5 μF和10 μF,开关频率可能选10 kHz和20 kHz。
为了对比分析L 型谐波抑制器和LCL 型谐波抑制器对网侧谐波电流的抑制效果,取L=L+Lg=1.536 mH,R=1.2 Ω,Cf=10 μF,分别绘制变换器的并网电流与输出电压的波特图,如图4所示。

图4 相同电感量下的幅频响应曲线Fig.4 Amplitude-frequency response curves with the same value of inductance
由图4 可以看出总电感量相同时,在高频段LCL 型谐波抑制器对注入到电网的谐波电流的衰减幅度远远大于L型谐波抑制器,这说明在抑制网侧谐波电流方面LCL 型谐波抑制器有着明显的优势,特别是在开关频率较低的大功率场合,达到网侧谐波电流要求所需的总电感量LCL 型谐波抑制器远小于L 型谐波抑制器,这将在很大程度上减小谐波抑制装置的体积、损耗和成本。
因此在总电感量相同的情况下,和L 型谐波抑制器相比,在抑制网侧谐波电流方面LCL型谐波抑制器有着绝对的优势。
4 系统仿真分析验证
4.1 仿真模型参数的选取
在PSIM中搭建了整个系统的仿真模型[10-12],其主要参数为:电网线电压380 V,无功补偿容量±10 kvar,基波频率50 Hz,载波频率10 kHz,直流侧电压630 V,直流侧电容330 μF。
谐波抑制器参数的选取按照上述理论来计算:
1)如果本系统模型按照L 型谐波抑制器设计,则通过计算得出L 的取值范围为:0.54 mH <L <1.74 mH,因此实际仿真模型中的L值在此范围选取;
2)如果本系统模型按照LCL 型谐波抑制器设计,则通过计算和综合考虑仿真调试的结果可得:L1=1.28 mH,L2=0.256 mH,R=1.2 Ω,Cf=10 μF。
4.2 L和LCL型谐波抑制器滤波效果对比分析
为了对比分析L 和LCL 型谐波抑制器的性能,主要是对在保持总电感量相同时情况下谐波抑制效果的对比分析。
根据前文谐波抑制器参数计算结果,首先取L=L1+L2=1.536 mH,观测总电感量相同时谐波抑制效果的差别,LCL 型谐波抑制器的具体参数为:L1=1.28 mH,L2=0.256 mH,R=1.2 Ω,Cf=10 μF。
L型谐波抑制器网侧和变换器侧三相电流的波形及其FFT 分析分别如图5、图6 所示。其中ICa,ICb,ICc为逆变器输出的补偿电流,ICas,ICbs,ICcs为输入电网的补偿电流。

图5 L谐波抑制器下三相补偿电流波形Fig.5 Three phase compensating current waveforms based on L type harmonic current suppressor

图6 L谐波抑制器下三相补偿电流FFT分析Fig.6 Three phase compensating current FFT analysis based on L type harmonic current suppressor
由图5、图6 可以看出输入电网的电流谐波含量和变换器端输出的电流谐波含量相同约为4.2%,高频谐波主要分布在fsw,2fsw,3fsw,4fsw附近。
基于LCL 型谐波抑制器的网侧和逆变器侧三相电流的波形及其FFT 分别见图7、图8。

图7 LCL谐波抑制器下三相补偿电流波形Fig.7 Three phase compensating current waveforms based on LCL type harmonic current suppressor

图8 LCL谐波抑制器下三相补偿电流FFT分析Fig.8 Three phase compensating current FFT analysis based on LCL type harmonic current suppressor
由图7 和图8 可以看出,网侧补偿电流波形明显更加接近正弦波,其谐波电流含量约为1.4%,较逆变器侧明显降低,取得了很好的谐波抑制效果。
5 实验结果
逆变器实验系统带阻感性负载。具体实验参数为:隔离变压器变比K=380∶340,阻尼电阻R=2.8 Ω,变压器漏感Lg=0.8 mH,直流母线电压UDC=760 V,逆变器侧电感L=4 mH,直流侧电容C=2 200 μF,电容Cf=10 μF,开关频率fsw=9.6 kHz。
实验中L 型谐波抑制器由制作的4 mH 电感和0.8 mH 的隔离变压器漏感组成,即L=4+0.8=4.8 mH。采用L滤波的逆变器侧和网侧补偿电流的波形如图9所示。

图9 L谐波抑制器下A相逆变器侧和电网侧补偿电流波形Fig.9 Inverter-connected and grid-connected compensating current waveforms of A phase based on L type harmonic current suppressor
从图9可以看出逆变器侧和网侧电流波形基本一致,谐波抑制效果不明显。
采用L型谐波抑制器的补偿电流FFT分析情况如图10所示。
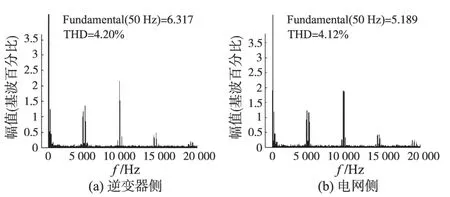
图10 L谐波抑制器下A相逆变器侧和电网侧补偿电流FFT分析Fig.10 Inverter-connected and grid-connected compensating current FFT analysis of A phase based on L type harmonic current suppressor
图10 a为逆变器侧补偿电流FFT分析,图10b为电网侧补偿电流FFT分析,可以看出谐波电流主要分布在开关频率及其整数倍附近,总谐波含量约为4.1%。
采用LCL 型谐波抑制器时逆变器侧和网侧补偿电流的波形如图11所示。

图11 LCL谐波抑制器下A相逆变器侧和电网侧补偿电流波形Fig.11 Inverter-connected and grid-connected compensating current waveforms of A phase based on LCL type harmonic current suppressor
从图11 可以看出网侧电流波形明显优于逆变器侧,说明LCL型谐波抑制器起到了良好的谐波抑制效果。
采用LCL 型谐波抑制器的补偿电流FFT 分析情况如图12所示。

图12 LCL谐波抑制器下A相逆变器侧和网侧补偿电流FFT分析Fig.12 Inverter-connected and grid-connected compensating current FFT analysis of A phase based on LCL type harmonic current suppressor
图12 a为逆变器侧补偿电流FFT分析,图12b为电网侧补偿电流FFT分析,可以看出逆变器侧谐波电流主要分布在开关频率及其整数倍附近,总谐波含量为6.29%,经LCL 型谐波抑制器之后开关频率及其整数倍附近的高频谐波被大幅衰减,并网电流谐波含量为2.32%(<5%),并网电流质量非常好。
6 结论
本文主要对静止同步补偿器LCL 型谐波抑制器的数学模型进行详细分析,并介绍了LCL型谐波抑制器新设计方法的思路和步骤,而后在仿真实例中按照上述步骤来设计LCL 型谐波抑制器的各个参数,并进行了仿真实验。
在保持总电感量相同的情况下,分析研究了L 型谐波抑制器和LCL 型谐波抑制器对谐波的抑制效果,并得出LCL型谐波抑制器的谐波抑制效果显著,优势突出。
最后通过实验平台在感性负载下进行了无功补偿实验,并对L型谐波抑制器下和LCL型谐波抑制器下的逆变器侧和网侧波形进行FFT 分析,得出LCL型谐波抑制器能很好地抑制高次谐波达到并网的要求,该研究对电流谐波抑制技术在电力系统并网应用中起到重要的作用。
[1] 王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2005.
[2] 陈坚.电力电子学──电力电子变换和控制技术[M].第2版.北京:高等教育出版社,2002.
[3] Wu E,Lehn P W.Digital Current Control of a Voltage Source Converter with Active Damping of LCL Resonance[J].IEEE Trans.on Power Electronics,2006,21(5):1364-1373.
[4] Lindgren M,Svensoon J.Connecting Fast Switching Voltagesource Converters to the Grid-harmonic Distortion and its reduction[C]//IEEE Stock Power Tech Conference,Stockholm,1995:191-195.
[5] 同向前,焦妍莹,申炜.静止同步补偿器滤波电感的选择[J].电力电子技术,2007,41(2):93-95.
[6] Wang Timoty CY,Ye Zhihong,Gautam Sinha,et al.Output Filter Design for a Grid-interconnected Three-phase Inverter[C]//Power Electronics Specialists Conference,2003 IEEE 34th Annual,2003,2:779-784.
[7] 孙蔚.LCL 滤波的PWM 整流器控制策略研究[D].北京:中国矿业大学,2009.
[8] 魏星,肖岚,姚志垒,等.三相并网逆变器的LCL 型滤波器设计[J].电力电子技术,2010,44(11):13-15.
[9] 刘飞,查晓明,段善旭.三相并网逆变器LCL型滤波器的参数设计与研究[J].电工技术学报,2010,25(3):110-116.
[10]熊卿.配电变压器一体化静止无功补偿器(D-STATCOM)关键技术研究[D].武汉:华中科技大学,2011.
[11]荣飞.配电网静止同步补偿器技术研究[D].长沙:湖南大学,2008.
[12]佟艳.基于DSP 的静止无功发生器的研究[D].天津:天津大学,2007.

