混合直流系统中直流侧故障暂态电流的解析表达与故障特性的研究

李 涛, 胡 迪, 刘宏达, 杨 为, 陈 忠, 官玮平

(1.国网安徽省电力公司 电力科学研究院,安徽 合肥 230022;2.国网浙江省电力公司 宁波供电分公司,浙江 宁波 315000)

0 引言

常规直流输电[1-2]也被称作线性换流器高压直流输电(Line Commutated Converter Based on High Voltage Direct Current,LCC-HVDC)通常需要控制晶闸管的关断来实现换流,易发生换相失败,同时需要消耗大量的无功功率。柔性直流输电也被称作基于电压源换流器高压直流输电(Voltage Source Converter Based on High Voltage Direct Current,VSC-HVDC)[3-4],其工程经济成本较高,尤其是直流输电线路上配置的高压直流断路器其成本接近整个工程的1/3。

结合常规直流输电技术和柔性直流输电技术的优缺点,研究学者将两种输电技术相结合,提出了混合直流输电技术的概念[5-7]。混合直流输电技术可有效解决多直流馈入问题,避免换相失败,且可实现远距离、大容量的多端电能输送。但作为一种新兴的高压直流输电技术,混合直流尚无运行经验,对于含混合直流的多端交直流电网,故障运行技术是保障系统安全运行的首要问题。因此,研究混合直流输电系统的故障特性,明确其交直流侧故障传播的机理,具有重要的理论和工程意义。

混合直流输电系统中直流线路两端包含换相换流器(Line Commutated Converter,LCC)换流站和电压源换流器(Voltage Source Converter,VSC)换流站,故其直流故障特性分析可参考单一的LCC-HVDC系统或VSC-HVDC系统。针对传统LCC-HVDC系统中直流故障特征,文献[8-9]利用状态空间方程分析了该系统中直流线路短路时的故障电流表达式。文献[10]利用相位模型转换理论剖析了直流故障特征。文献[11]利用等效电路理论计算出直流线路故障时短路电流时域表达式。然而,上述方法均未详细考虑故障发生时送端LCC侧换流站触发角的动态变化对故障电流的影响。

同样,针对VSC-HVDC系统的故障特性,部分学者进行了详细地研究。文献[12-14]利用拉普拉斯变换理论构建了多端直流输电系统的等效模型,求解了直流线路故障电流的高频分量与其暂态平均值,剖析了故障电流的暂态特征。文献[15]利用电容充放电理论分析了直流侧故障时由VSC侧电容放电引起故障电流的变化特征。文献[16]将VSC型换流站等效为RLC型简单电路,利用叠加定理分析了系统模型并推导出直流侧故障电流解析表达式。然而,上述文献均没有考虑交流网络的影响。针对上述文献的研究不足,文献[17]提出了考虑交流网络阻抗的短路电流表达式,并分析了不同阻抗的取值对故障电流的影响。文献[18]解析了充分考虑VSC换流站中三相桥臂电流的短路电流表达式,探讨了直流侧故障电流的变化特征。但上述两种方法均没有考虑VSC换流站的控制策略对直流侧短路电流的影响。

部分学者对混合直流输电系统中直流线路短路电流进行了研究。文献[19]针对受端电网同时含有LCC换流站和模块化多电平换流器(Modular Multilevel Converter,MMC)换流站的混合直流输电系统,分别解析了高压阀组LCC出口短路和低压阀组MMC出口短路时的故障电流表达式,然而,该文献并没有详细分析两侧短路电流的变化特征。文献[20]考虑了LCC侧触发角的动态变化和VSC侧交流电流馈入至直流侧的分量,解析了两侧短路电流的表达式,然而,该文献只分析了单个LCC-HVDC或VSC-HVDC系统的故障电流表达式,并没有考虑混合直流输电系统中短路电流的变化特征。文献[21]针对LCC-MMC型混合直流输电系统首先建立了考虑LCC换流站和MMC换流站控制系统的复频域等效模型,然后计及直流输电线路的频域特性,推导出直流短路电流的复频域数值,最后利用拉氏反变换计算出短路电流的时域表达式。然而,该方法需要进行时域、频域以及复频域之间的数值转换,计算过程比较繁琐。

因此,本文建立了两端LCC/VSC型混合输电模型,利用拉氏变换理论获得了直流侧故障时系统等效模型,推导出两侧故障电流解析表达式。并从故障电流幅值、谐波等方面对比分析了三种高压直流系统中直流侧故障电流的变化特征。

1 系统拓扑与等效拉普拉斯变换电路

送端电网和受端电网分别由LCC换流站和VSC换流站构成的混合直流输电系统如图1(a)所示。图中送端电网通过Y/Δ变压器连接至送端LCC换流站,直流线路一端连接LCC换流站、另一端连接VSC换流站,受端VSC换流站通过Yg/Δ变压器连接至受端电网。忽略线路电容参数的影响,图1(b)给出了两端混合直流输电系统的等效电路图。其中：Ldc、Rd及Ld分别为直流线路的限流电抗器、电阻及电感;Ed、r分别为送端LCC换流站的等效内电动势、等效内阻;udc为直流侧电压。Ed和r的数学关系为

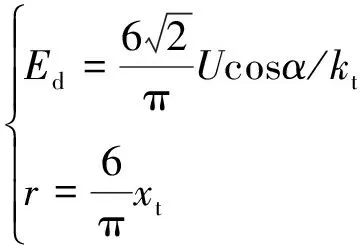
(1)

式中：U、kt、α及xt分别整流侧换流站的交流母线电压、变压器变比、触发角及换相电抗。

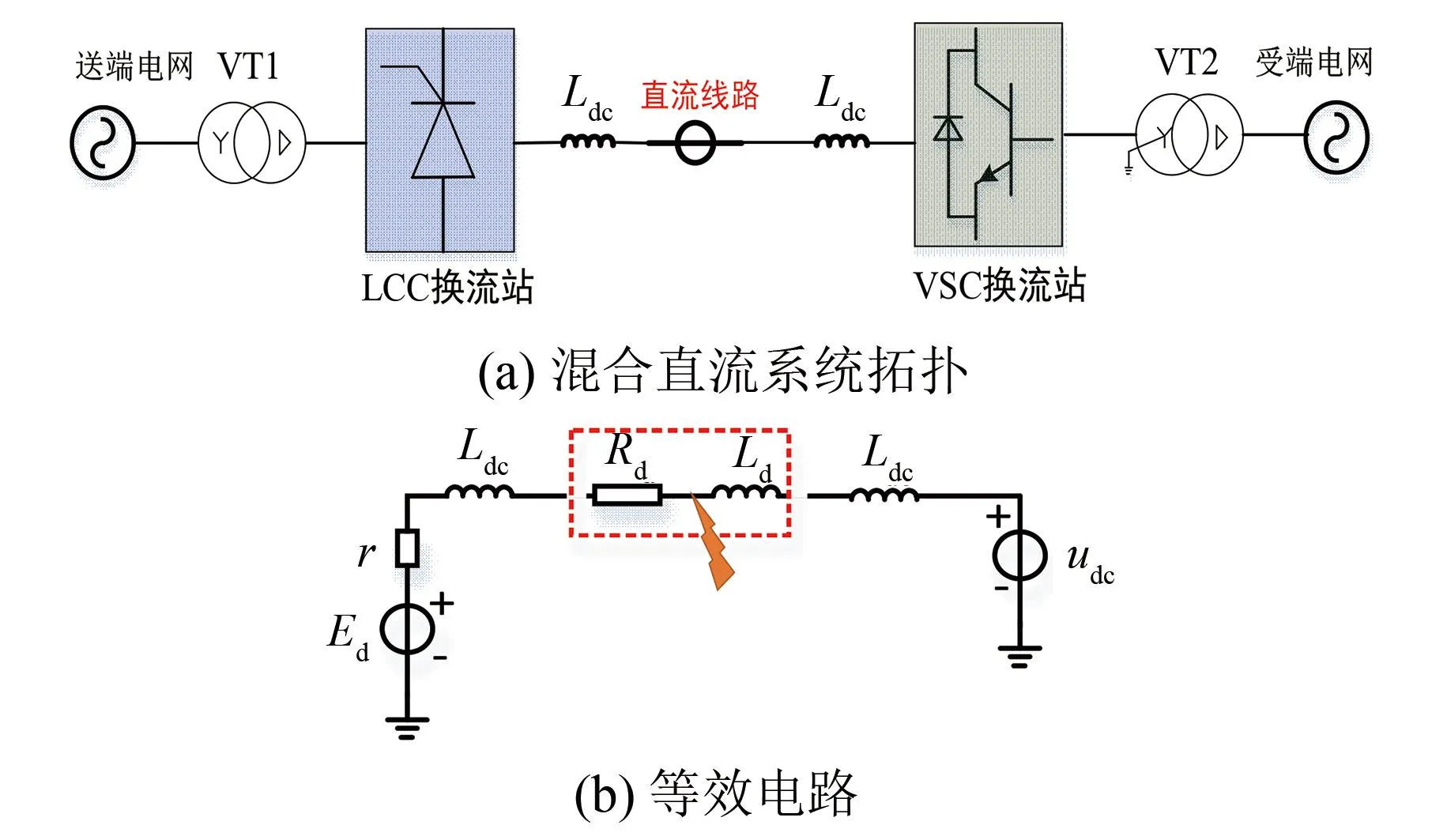
图1 系统拓扑与等效电路

对图1(b)所示的等效电路进行拉式分析,并考虑在非零的独立初始条件下附加电源函数的影响[22],拉式变换电路拓扑如图2(a)所示。令R10=r+Rd1,L10=Ld1+Ldc,R20=Rd2,L20=Ld2+Ldc,可得到其简化电路如图2(b)所示。

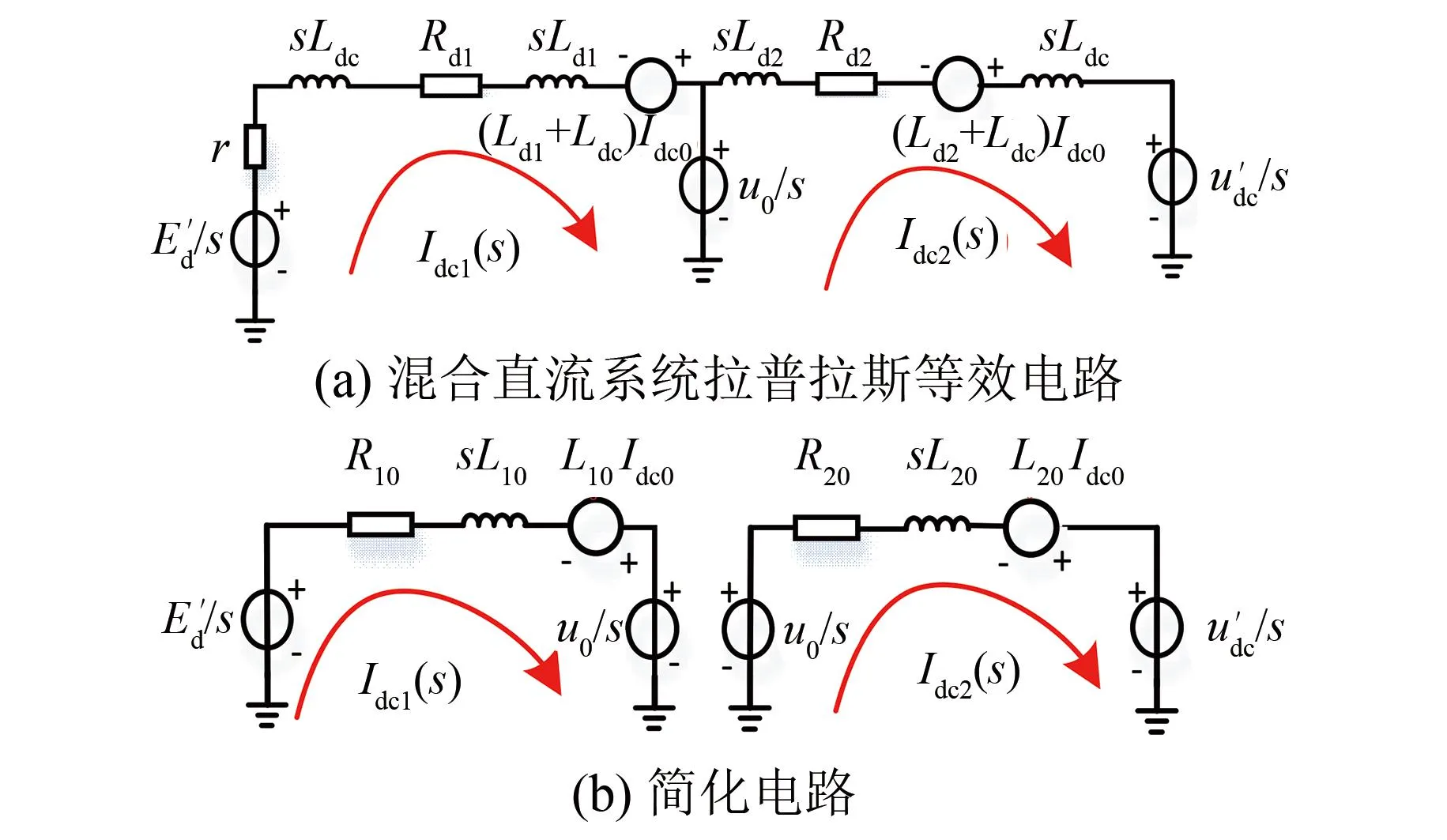
图2 拉普拉斯变换等效电路

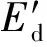
设定图2(b)中的环路电流为Idc1(s)和Idc2(s),可得环路电流方程为

(2)

求解上述环路电流方程,得到时域内的方程的解为

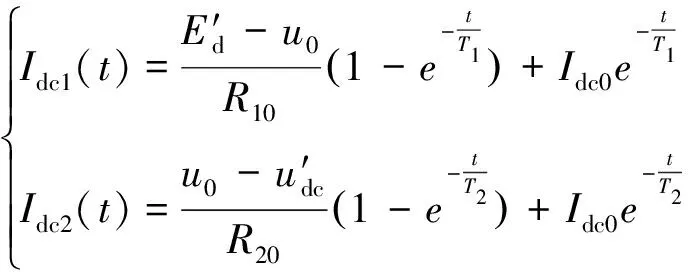
(3)

其中：

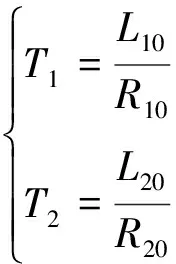
(4)

图3 LCC侧、VSC侧故障电流的仿真值和计算值

2 直流侧精确故障电流解析表达式

由于前述LCC侧、VSC侧故障电流表达式的计算值与仿真值存在一定的差异,故本节将着重考虑LCC侧换流站触发角的动态变化过程和VSC侧换流站交流电流馈入至直流侧的成分。

2.1 考虑触发角动态变化过程的LCC侧故障电流表达式

利用最小二乘法对触发角的非线性过程做近似线性化处理,定义直流系统故障后LCC侧换流站触发角变化函数为f(α),可得：

f(α)=k(α-α0)+cosα0

(5)

式中：α0和α分别为故障前后的触发角;k为变化系数。

由式(5)可知,k的取值至关重要。定义以下最小函数存在于触发角变化区间[α0,α1]：

minS=min‖f(α)-cosα‖2

(6)

对上式做最小二乘法处理,可得：

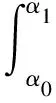
(7)

式(7)两边同对k求导,可得：

(8)

当∂S/∂k=0时,由式(8)可得：

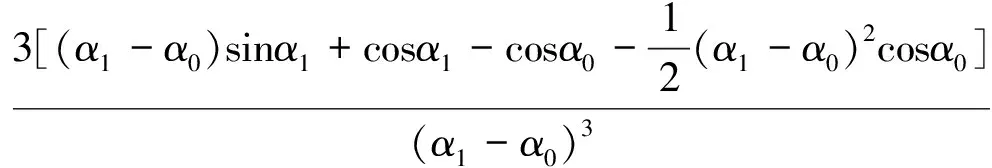
(9)

结合式(1)、(5)和(9)可得故障后LCC侧换流站的等效电动势为

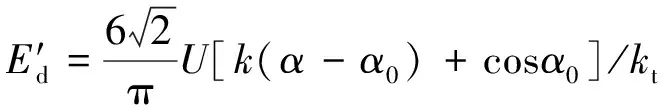
(10)

最后,将式(10)代入式(3)可得到新的短路电流表达式。根据以上分析,得到了考虑触发角近似线性化过程的LCC侧故障电流的计算值,其与仿真值波形对比如图4所示。由图可知,所提的短路电流表达式误差较小,验证了上述分析的正确性。

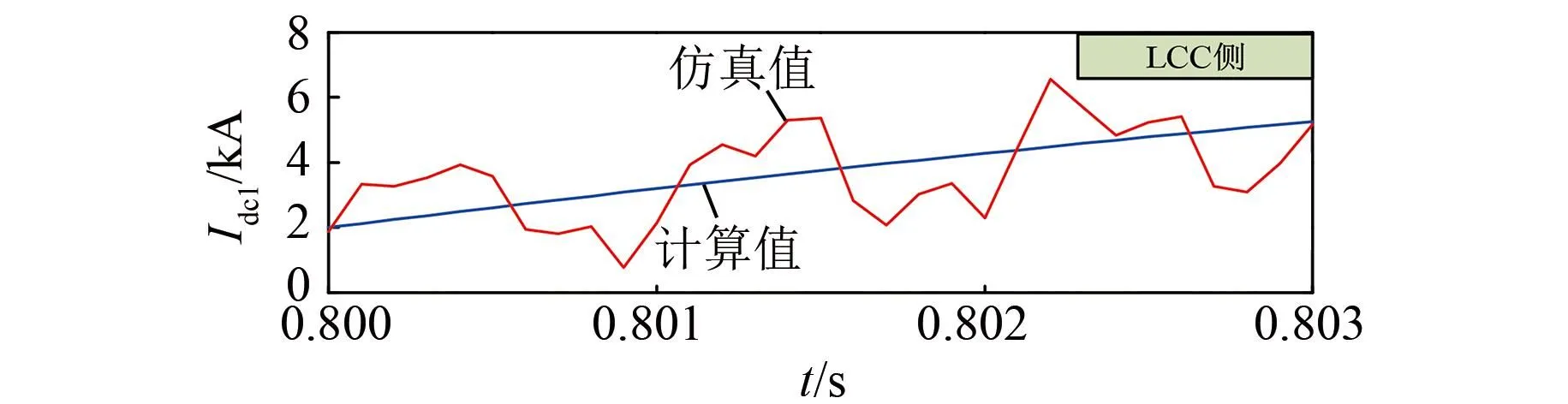
图4 考虑触发角线性化的LCC侧故障电流的仿真值和计算值

2.2 考虑交流电流馈入至直流侧成分的VSC侧故障电流表达式

逆变侧VSC换流站其直流侧和交流侧的等效电路如图5所示。

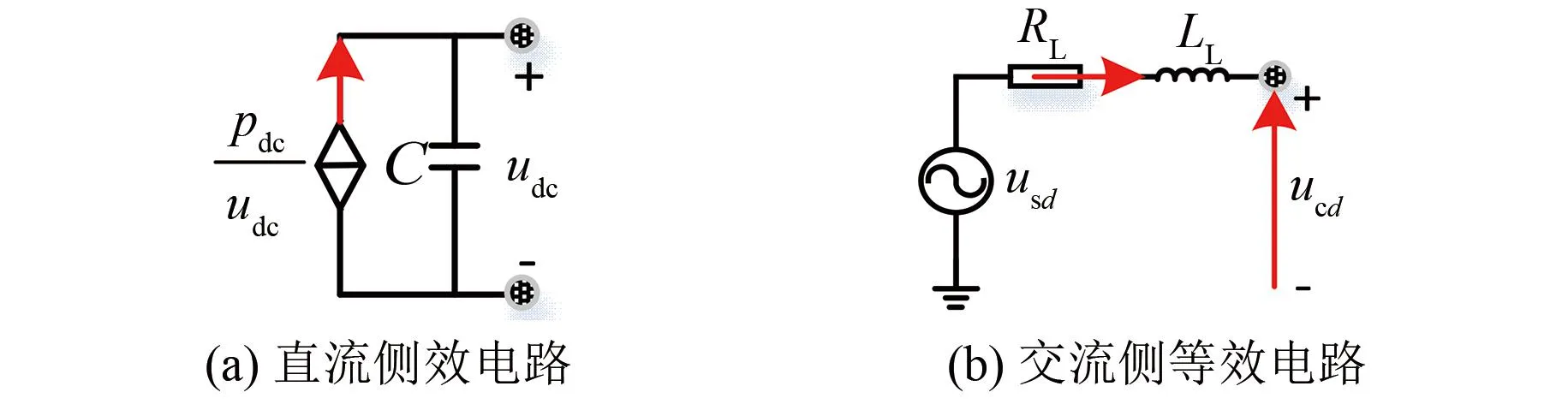
图5 逆变站VSC的直流/交流等效电路

图5中：pdc、usd及ucd分别为直流功率、VSC侧交流电网电压d轴分量以及换流站出口电压d轴分量;RL、LL分别为交流线路的电阻、电感。

根据KCL和KVL定理,可得：

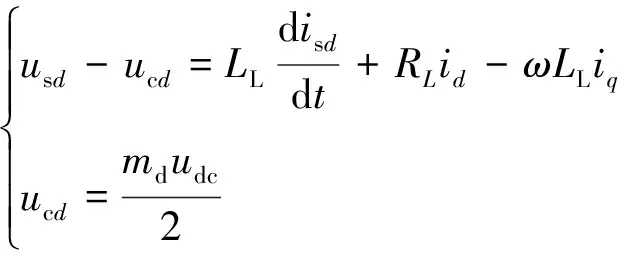
(11)

式中：md为调制比;id、iq分别为交流电流的d、q轴分量。

通常,VSC侧换流站的调制比通过内环PI控制器得到,其表达式为

(12)

式中：udcN和idref分别为直流电压的额定值和d轴电流的参考值;ki和kp分别为积分系数和比例系数。

由于VSC侧换流站的分压电容相对较大,因此假设在直流故障后的初始阶段,VSC侧的直流电压不发生较大变化[10-12]。此外,VSC站内环PI控制器也不会转入限流控制模式。因此,可根据故障前的条件对式(11)和(12)建立小信号模型,即：

(13)

式中：udc0为直流电压的初始值;md0为调制比的初始值。

求解式(13)可得：

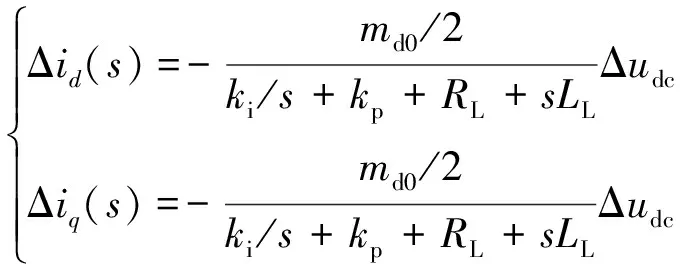
(14)

根据理想状态下的功率守恒定律可知：

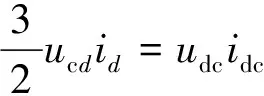
(15)

化简式(15)可得：

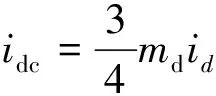
(16)

对式(16)做小信号分析可得：

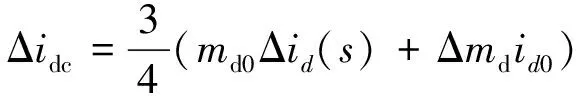
(17)

式中：id0为电流id的初始值。

忽略并网电压积分项和q轴分量的影响,结合式(13)、(14)和(17)可得：

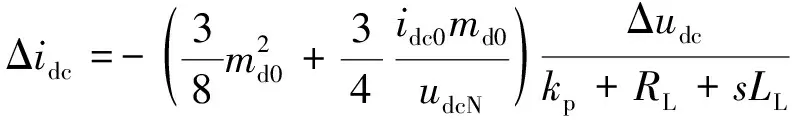
(18)

式(18)即为交流电流馈入至直流侧的分量,结合式(3)可得VSC侧新的故障电流表达式为

(19)

式中：T3=LL/(RL+kp)。

根据式(19),可得考虑交流电流馈入的VSC侧故障电流的计算值,其与仿真值的对比如图6所示。由图可知,当考虑交流电流馈入时,仿真值与计算值之间的差异显著减小,验证了上述分析的正确性。

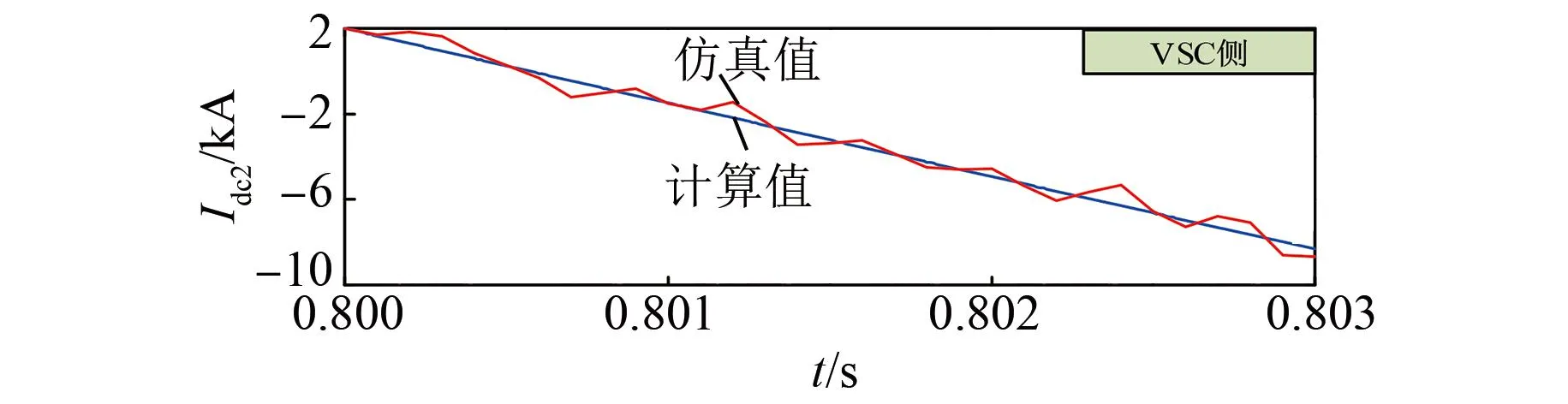
图6 考虑交流电流馈入至直流侧的VSC侧故障电流的仿真值和计算值

2.3 接地电阻故障

图7 考虑接地电阻的等效拉普拉斯变换电路

短路电流表达式的求解主要基于金属性接地故障,因此对接地电阻故障时短路电流表达式的解析情况进行分析。基于图2的等效电路,得到了接地电阻故障下直流系统的等效电路如图7所示,其中Rf为接地电阻。

接地电阻故障下直流系统两侧故障电流表达式为

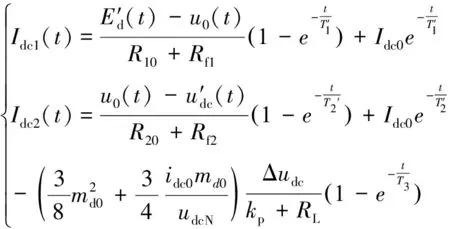
(20)

其中：

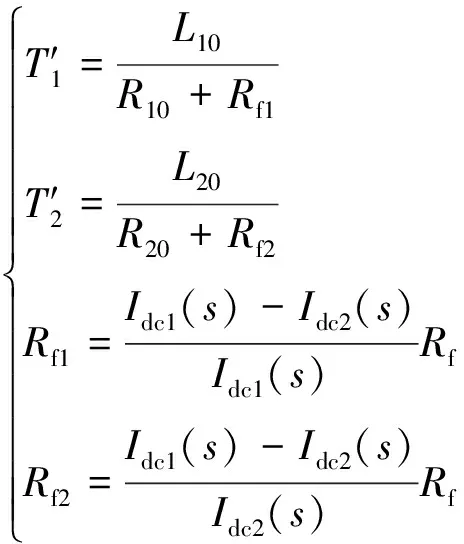
(21)

由式(20)可知,若能求解出Rf1和Rf2,则短路电流表达式将被较好解析。对图7(b)所示的简化电路做进一步简化得到图8所示的无源等效电路,可得：

(22)

将式(22)代入式(21),可得：

(23)

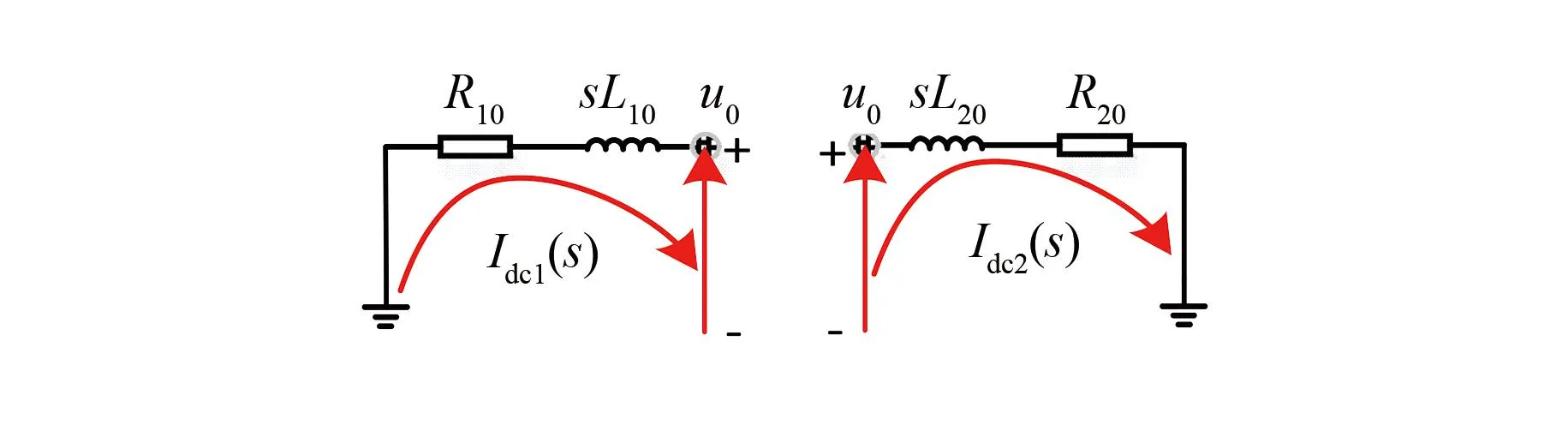
图8 无源等效电路

根据上述计算即可得到接地电阻故障下的短路电流表达式。

3 混合直流系统与传统LCC-HVDC、VSC-HVDC系统直流侧故障特征比较

3.1 故障解析表达式在不同系统中的应用

为了验证所提的直流侧故障解析表达式在不同直流系统中的适用性进行了仿真。仿真中,三种直流系统的电压等级为300 kV,额定直流电流为2 kA。三种直流输电系统中直流侧故障电流的计算值和仿真值波形如图9所示。由图可知,通过所提故障电流解析表达式得到的计算值波形与仿真值波形在故障初始阶段基本变化趋势一致,误差较小。对于LCC-HVDC系统,整流侧故障电流的计算值和仿真值在故障发生2.1 ms内变化趋势基本吻合;对于VSC-HVDC系统,整流侧故障电流的计算值和仿真值在故障发生4 ms内变化趋势基本吻合;对于LCC/VSC混合系统,整流侧故障电流的计算值和仿真值在故障发生7 ms内变化趋势基本吻合。

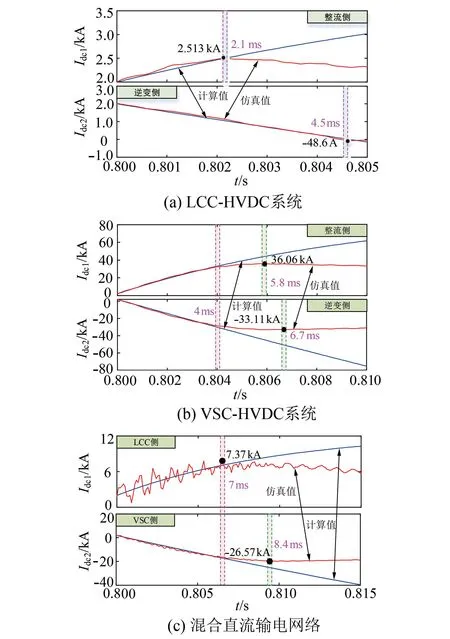
图9 三种不同输电网络的直流侧故障特性比较

然而,随着故障时间的延长,故障电流的计算值与仿真值误差较大。以LCC/VSC混合系统为例,故障发生7 ms后,故障电流的计算值与仿真值出现了明显差异。这是由于故障发生7 ms后两侧故障电流呈现非线性变化,而上述对于短路电流表达式都是基于线性化过程分析得到的,故7 ms后故障电流的计算值需做分段线性化处理。

LCC-HVDC系统和VSC-HVDC系统的分析与上述一样。同样需对非线性化的故障电流做分段线性化处理,再利用本文所提方法求得不同阶段的短路电流表达式。综上,本文所提方法优先适用于故障发生的初始阶段,即故障电流呈线性趋势变化的阶段,其可为直流线路的保护原理提供一定的参考。

3.2 不同系统直流侧故障电流的变化特征

由图9可知不同系统的直流侧故障电流的变化特征不一样。因此,需对不同系统中直流侧故障电流的变化特征进行分析。

仿真设定直流线路的中间段在0.8 ms发生短路故障。由图9(a)可知,传统的LCC-HVDC输电系统中整流侧故障电流约在故障后的2.1 ms达到最大值2.513 kA,逆变侧故障电流约在4.5 ms达到最小值-48.6 A。此时,两侧故障电流的变化率分别为0.244 kA/ms和-0.455 kA/ms。

由图9(b)可知,VSC-HVDC输电系统中整流侧故障电流约在5.8 ms达到最大值36.06 kA,逆变侧故障电流约在6.7 ms达到最小值-33.11 kA。此时,两侧故障电流的变化率分别为5.872 kA/ms和-5.24 kA/ms。

由图9(c)可知,混合直流输电系统中整流侧故障电流约在7 ms达到最大值7.37 kA,逆变侧故障电流约在8.4 ms达到最小值-26.57 kA。此时,两侧故障电流的变化率分别为0.767 kA/ms和-3.401 kA/ms。

综上可知,相较于传统的LCC-HVDC系统,混合直流输电系统中VSC-HVDC子系统的接入延长了LCC-HVDC子系统直流故障电流上升至最大值的时间,增加了两侧换流站直流故障电流的幅值;相较于传统的VSC-HVDC系统,混合直流输电系统中LCC-HVDC子系统的接入,延长了VSC-HVDC子系统直流故障电流上升至最大值的时间,降低了两侧换流站故障电流的幅值。

另外,根据三种系统中故障电流的变化速率可知,VSC-HVDC系统中故障电流的变化速度最快,其次为LCC/VSC-HVDC混合系统,LCC-HVDC系统中故障电流的变化速度最慢。

为了对比不同系统故障电流的谐波特征,对LCC-HVDC、VSC-HVDC以及LCC/VSC-HVDC混合系统中故障电流进行了谐波分析,其结果如图10～12所示。选定时间段为0.8-0.9 s的故障电流做谐波分析。由图可知,LCC-HVDC系统中整流侧故障电流谐波畸变率为234.48%,逆变侧故障电流谐波畸变率为326.61%;VSC-HVDC系统中整流侧故障电流谐波畸变率为50.33%,逆变侧故障电流谐波畸变率为33.66%;LCC/VSC-HVDC混合系统中整流侧故障电流谐波畸变率为241.67%,逆变侧故障电流谐波畸变率为185.09%。

分析上述谐波数据可知,相较于传统的LCC-HVDC系统,混合直流系统中受端VSC-HVDC子系统的接入降低了送端LCC-HVDC子系统的谐波畸变率;相较于VSC-HVDC系统,混合直流系统中送端LCC-HVDC子系统的接入,增加了受端VSC-HVDC子系统的谐波畸变率。

综上所述,三种直流输电方式的直流侧故障特征差异明显,可根据实际需求借鉴相应的故障电流波形,提供相应的保护原理或提出相应的抑制故障电流变化的控制策略。

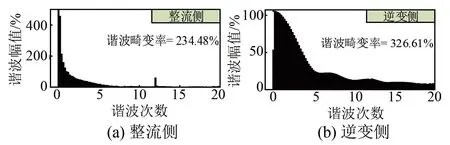
图10 LCC-HVDC系统直流侧故障电流谐波分析

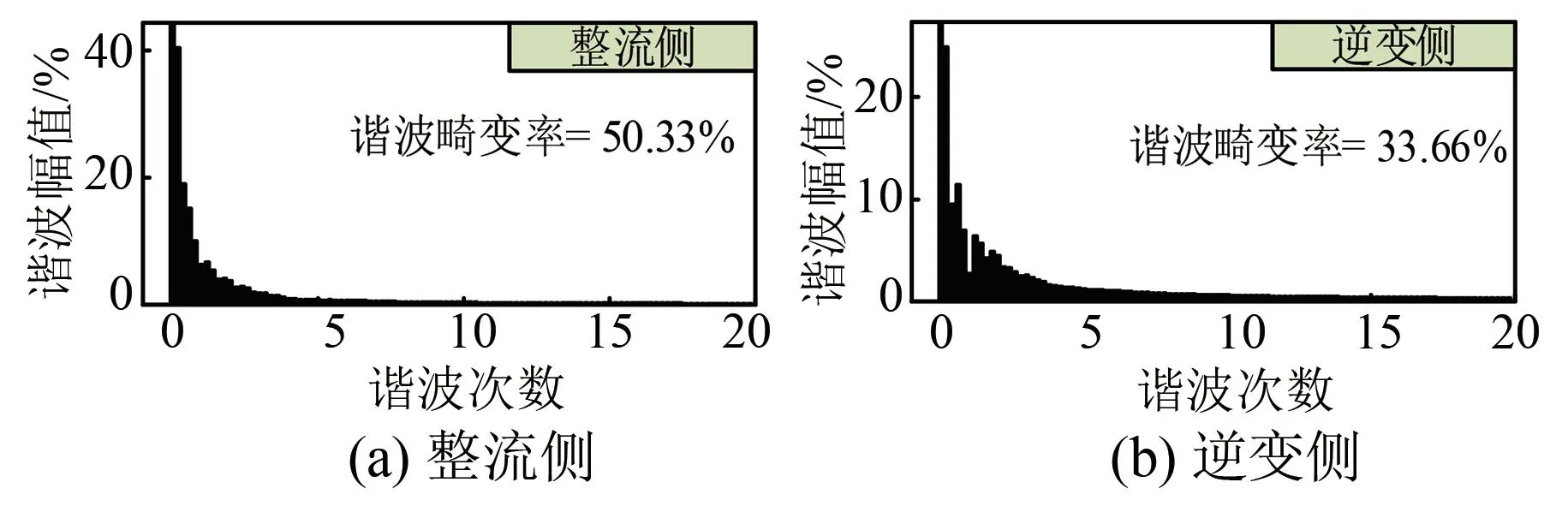
图11 VSC-HVDC系统直流侧故障电流谐波分析

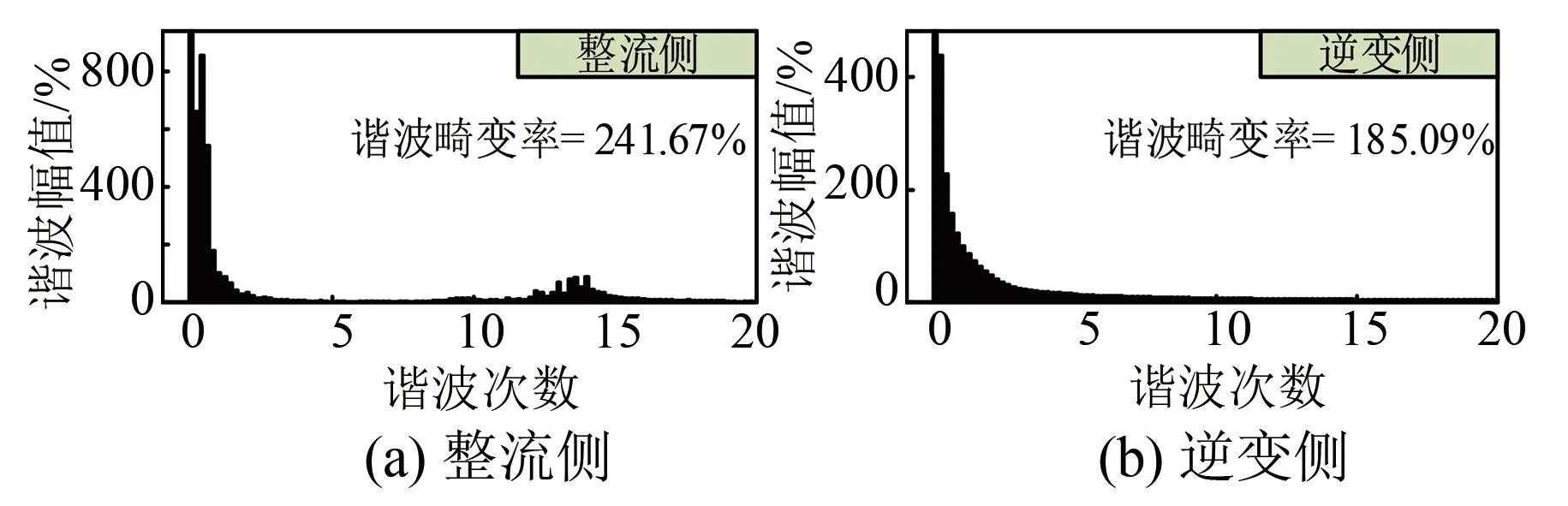
图12 LCC/VSC-HVDC系统直流侧故障电流谐波分析

4 仿真验证

为了验证上述理论分析和设计的正确性,基于MATLAB/Simulink软件搭建了图1(a)所示的两端混合直流输电拓扑。仿真中设定直流线路在0.8 s时发生短路故障,故障点的位置位于1/2线路处。具体仿真参数如表1所示。

表1 仿真参数

4.1 不同时间尺度的短路电流表达式的验证

图13中为1 ms、2 ms和15 ms时间窗口的两侧短路电流仿真值和计算值比较波形。由图13(a)和13(b)可知,两侧短路电流的计算值与仿真值的变化趋势基本一致。由图13(c)可知,两侧故障电流计算值和仿真值的变化趋势在故障发生的7 ms内基本保持一致,7 ms后两侧故障电流的实际变化趋势将呈现非线性化。本文求解短路电流的过程都是以线性化趋势的数值代入,这是7 ms以后计算值与仿真值出现差异的主要原因。但是,这种差异并不影响短路电流表达式的实用性。要想准确获得7 ms以后故障电流的波形,可先将其分段线性化,再使用本文所提的故障分析方法进行求解。

图13 不同时间窗口的短路电流的仿真值与计算值

4.2 不同故障点位置的短路电流表达式的验证

上述理论和仿真的故障点位置都位于1/2线路处,因此还需进一步进行验证本文所提方法对不同故障点位置的短路电流的适用性。基于此进行了仿真分析,得到了不同故障点处两侧短路电流的计算值和仿真值波形如图14所示。由图可知,故障点位置位于直流线路的1/4和3/4处时,两侧短路电流仿真值和计算值波形的变化趋势也基本保持一致。

图14 不同故障点处两侧短路电流的仿真值与计算值

4.3 不同接地电阻的短路电流表达式的验证

图15(a)～(d)分别为接地电阻为10 Ω、20 Ω、30 Ω以及40 Ω情况下短路电流仿真值和计算值波形。由图可知,四种接地电阻取值情况下短路电流计算值与仿真值的变化趋势基本一致,尤其是受端VSC侧短路电流计算值与仿真值波形基本吻合,其平均误差约为100 A。

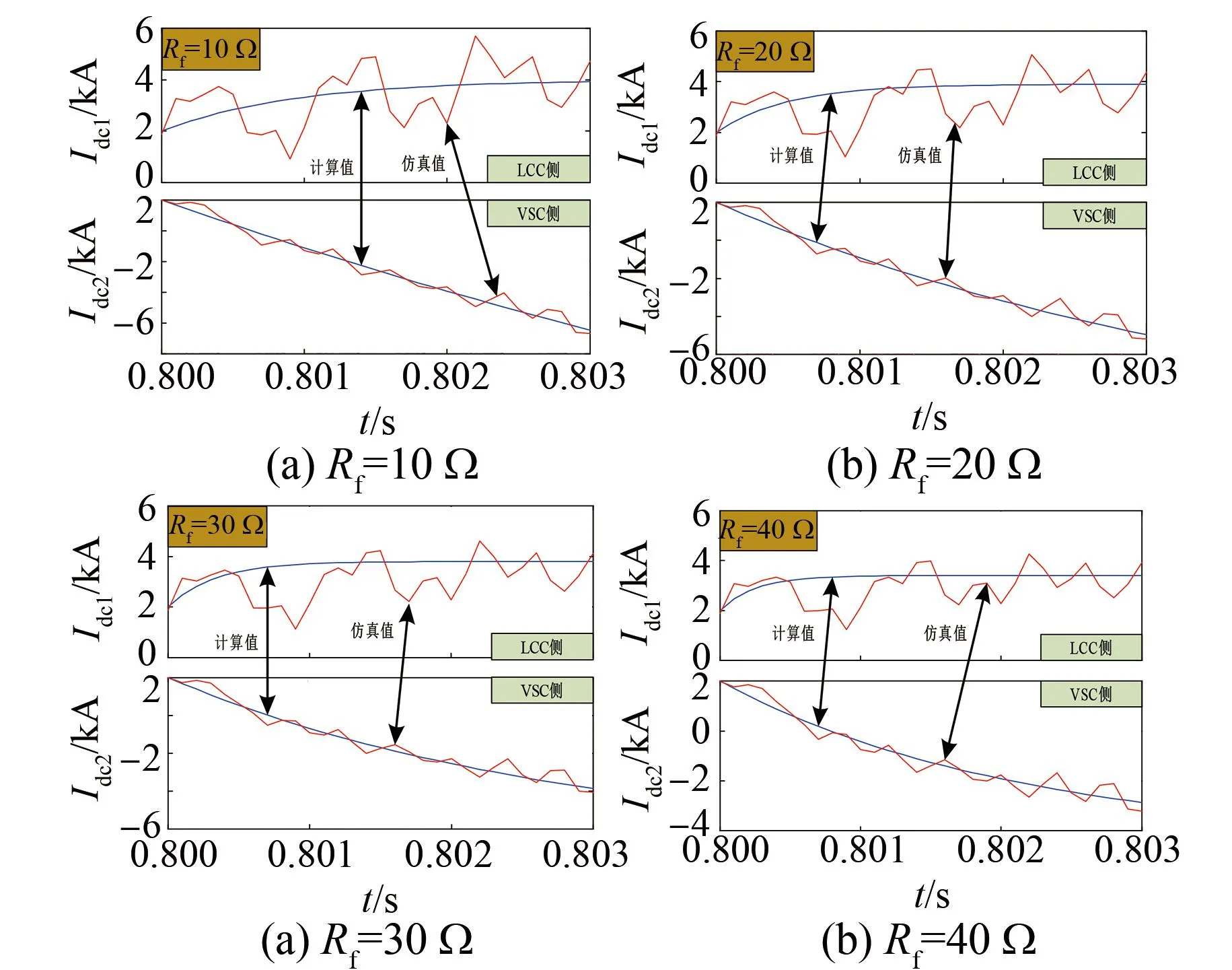
图15 不同接地电阻下两侧短路电流的仿真值与计算值

5 结语

本文提出了一种适用于混合直流系统中充分考虑LCC侧换流站触发角的动态变化以及VSC侧换流站交流电流馈入至直流侧的故障分析方法,并将其与传统的LCC-HVDC和VSC-HVDC系统的故障特性进行对比。得出以下结论：

(1) 本文所提故障分析方法的计算值与仿真值变化趋势基本一致,差异较小。尤其是VSC侧故障电流的计算值与仿真值的误差小于100 A;

(2) VSC-HVDC系统的直流侧故障电流幅值变化率最高,LCC/VSC-HVDC混合直流系统次之,传统的LCC-HVDC系统最小;

(3) 传统LCC-HVDC系统直流侧故障电流谐波畸变率最高,LCC/VSC-HVDC混合直流系统次之,传统的LCC-HVDC系统最小;

(4) 针对故障点的位置不同和接地电阻的数值变化,本文所提故障特性方法仍然适用;

(5) 本文所提的直流侧故障特性方法适用于故障发生7 ms以内的线性化过程,对于7 ms以后的非线性化过程需要使用所提方法进行分段线性化处理。

Research on Analytical Expression of DC Side Fault Transient Current and Fault Characteristics in Hybrid HVDC System

LI Tao1*, HU Di1, LIU Hongda2, YANG Wei1, CHEN Zhong1, GUAN Weiping1

(1.Electric Power Research Institute, State Grid Anhui Electric Power Co., Ltd., Hefei 230022, China;2.Ningbo Power Supply Branch, State Grid Zhejiang Electric Power Co., Ltd., Ningbo 315000, China)

Keywords： line-commutated converter based on high-voltage direct current (LCC-HVDC); voltage source converter based on high voltage direct current (VSC-HVDC); hybrid HVDC transmission; DC fault characteristics; trigger angle; the feeding of AC current

With the development of the power grid, more and more voltage source converter based on high voltage direct current (VSC-HVDC) will be fed into the load center, forming a pattern where line-commutated converter based on high-voltage direct current (LCC-HVDC) and VSC-HVDC are mixed and fed into the grid. When two types of HVDC transmission systems form the same transmission network, they exhibit different fault characteristics from single-infeed HVDC transmission systems. Therefore, studying the fault characteristics of hybrid multi-terminal HVDC system, especially solving the analytic expressions of the fault current on the LCC-side and the VSC-side when the DC side fails, has important theoretical and engineering significance for the research of the hybrid multi-terminal HVDC system.

Firstly, this paper establishes the equivalent Laplace transform model of the three-terminal LCC-VSC-VSC network, and analyzes the simple expression of the short-circuit current on both sides when the DC line fails. Secondly, considering the shortcomings of the simple current expressions on both sides, the least square method is used to linearize the trigger angle on the LCC-side and the common inner-loop PI controller model on the VSC-side is used to analyze the AC current fed to the DC side, which obtain the accurate expression of fault current on both sides. Then, the variation characteristics of DC side fault current in three HVDC systems are comparatively analyzed in terms of fault current amplitude and harmonic. Finally, the correctness of the proposed analytical expression of DC side fault current is verified by MATLAB/Simulink simulation.

Fig.1 shows the simulated and calculated waveforms within 15 ms during the post-fault. As observed, the variation trend between the simulated value and the calculated value is basically the same within 7 ms of the fault occurrence, because the dynamic process of the fault current during this period can be approximately considered to be linear. The fault analysis approach described in this paper is solely directed at the linearized process at the beginning of the fault, it concentrates on assessing the 7 ms fault current waveform during the post-fault. For the nonlinear process of the whole fault process, it is necessary to use the data of different stages and the method of this paper to solve the short-circuit current expression. For example, if the current expression between 7-15 ms is to be solved, it is necessary to use the data at 7 ms as the initial value and the data at 15 ms as the final value. The purpose of this study is to solve the short-circuit current expression from the fault occurrence to the maximum value, which provides a theoretical reference for the protection principle of hybrid HVDC system.

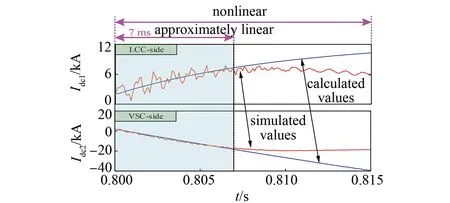
Fig.1 Simulated and calculated values of short-circuit current in different time window