点阵夹芯圆柱壳自由振动分析的波有限元方法
韩少燕, 高汝鑫
(1. 西安交通大学城市学院 机械工程学院, 西安 710018;2. 北京理工大学 先进结构技术研究院, 北京 100081;3. 大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024)
0 引 言
点阵夹芯结构被认为是最具应用前景的下一代轻量化多功能结构形式之一,其有着传统材料结构所不具备的力学性能,例如较高的比刚度、比强度、能量吸收能力和性能可设计等[1].常见的点阵夹芯结构单胞的拓扑构型有金字塔型[2]、四面体型[2]、Kagome型[2]、三维全三角型[3]和八面体型[4]等.点阵夹芯结构,如点阵夹芯梁、板和壳结构,因其上述的优异性能已成功应用于航空航天领域[5].国内外学者针对点阵夹芯结构的力学和热学性能开展了众多研究[6-7].根据点阵夹芯结构的构成特点,其多用于抗冲吸能结构设计[8].点阵夹芯结构应用于航空航天、船舶等机械结构时,通常会遭遇复杂的振动环境,所以研究点阵夹芯结构的振动特性是十分必要的.近年来,学者们针对点阵夹芯结构的线性和非线性振动开展了相关研究工作[9-11].
波在周期结构中传播时满足Bloch定理[12],点阵夹芯结构通常具有周期性,故波有限元法为周期结构的振动分析提供了一种快速求解方案.然而,波有限元方法往往面临较多的数值问题,通常可分为三类[13]: ① 当频率较高时出现的有限元离散误差和色散误差[14]; ② 当胞元长度与变形波长相当时出现的空间离散和周期结构效应[12,15]; ③ 传递矩阵的条件数过大,矩阵病态导致本征值和本征向量无法求解[16].对于前两种数值问题,可以通过减小单元尺寸加密网格来避免;而传递矩阵数值病态的问题,就只能通过建立高精度的数值求解方法来解决.为此,学者们针对传递矩阵本征值和本征向量的求解提出了众多方法:Zhong和Williams[16]应用结构力学和最优控制理论的类比关系,提出了一种直接求解方法,该方法将传递矩阵的本征值的求解转化为两个非病态矩阵的广义特征值的求解;传递矩阵的本征值问题可以转化为回文二次特征值问题,Huang等[17]针对回文二次特征值问题提出了保结构算法;Wang等[18]进一步扩展了Zhong和Williams的直接求解法,突破了原方法只能处理单根的限制,使得该方法可以处理多重根问题.但是上述传递矩阵特征值的求解方法多用来处理较为简单的胞元或者自由度规模较小的传递矩阵,当矩阵规模较大时,上述方法会出现累积误差.鉴于上述原因,目前波有限元方法通常将较为规则的一维或二维单元作为单胞求解均质结构的振动分析问题[19-21],或用来处理胞元构型较为简单的周期(点阵)结构的振动分析问题[22-24].
本文基于波传播理论和有限元方法,针对点阵夹芯圆柱壳的自由振动分析,发展了波有限元方法.首先,根据自由波在圆柱壳轴向和周向的传播规律,基于波有限元方法建立了胞元的振动控制方程.该振动控制方程虽然建立在胞元自由度上,但可描述整个点阵夹芯圆柱壳的自由振动行为.其次,对于胞元振动控制方程,基于Neumann级数推导了约束刚度矩阵的逆矩阵的显式表达式,不仅提高了求逆效率,而且将振动控制方程中的频率分离出来,从而将点阵夹芯圆柱壳的固有频率求解转化为胞元边界自由度规模的二次特征值问题.最后,根据驻波形成的条件,给出了圆柱壳轴向和周向的波传播参数,进而求解二次特征值问题即可得到点阵夹芯圆柱壳的固有频率.相比于全尺寸有限元模型,本文的方法可显著降低计算模型的自由度规模,从而显著降低计算成本,提高计算效率,且没有数值病态的问题.另外,推导过程不指定胞元的结构形式,且其刚度矩阵和质量矩阵可以方便地从任意的商业有限元软件中导出,便于工程应用.
1 胞元的波有限元控制方程
考虑点阵夹芯圆柱壳的自由振动,其中一个胞元的有限元模型如图1所示,该胞元的有限元振动方程可以写为
Dq=f,
(1)
其中
D=K-ω2M
(2)
为胞元的动刚度矩阵,q为胞元的节点自由度向量,f为胞元的节点力向量,K和M分别为胞元的刚度矩阵和质量矩阵,ω为点阵夹芯圆柱壳自由振动的圆频率.
根据图1对节点自由度的划分,可以将式(1)写为分块的形式:
(3)
其中
(4)
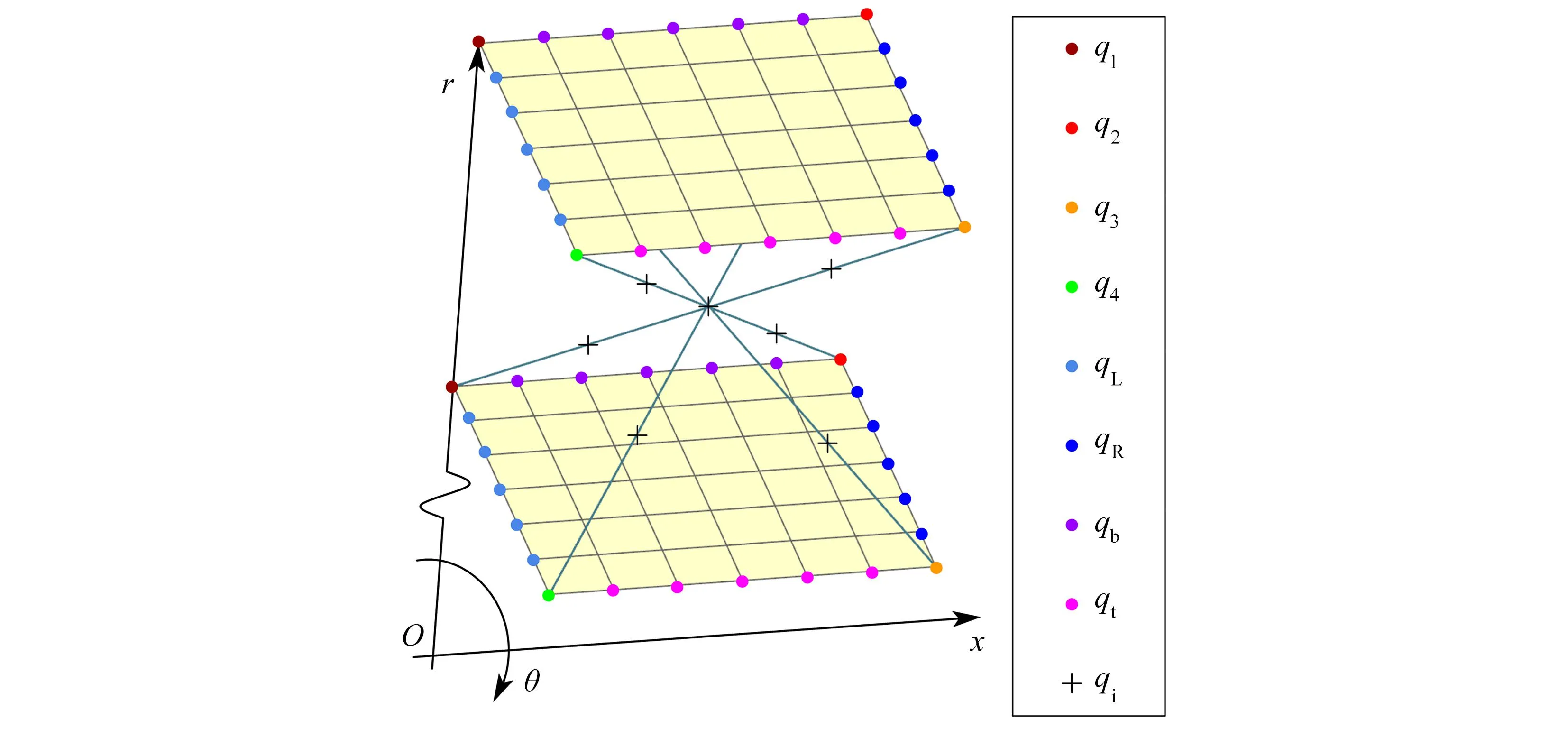
图1 点阵夹芯圆柱壳胞元的有限元模型
胞元内部节点作用力为零,即fi=0,展开式(3)第2行并移项可得
(5)
将式(5)代入到式(3)第1行可得
(6)
根据Bloch-Floquet定理,胞元相邻边界上的节点自由度向量具有以下关系:
q2=λxq1,qR=λxqL,q4=λθq1,qt=λθqb,q3=λθλxq1,
(7)
其中λx和λθ分别为胞元在轴向和周向的波传播参数.
根据式(7)和(4),可以将qe表示为
qe=ΛQ,
(8)
其中
(9)
(10)
将式(8)代入式(6)得到
(11)
根据胞元力的平衡条件[25]有
(12)
(13)
(14)
将式(12)—(14)写为矩阵形式有
ΛHfe=0.
(15)
将式(11)代入式(15)有
(16)
其中
(17)
式(16)即为点阵夹芯圆柱壳胞元的波有限元控制方程.
2 约束动刚度矩阵的显式求逆
(18)
利用Neumann级数[26]将式(18)近似为
(19)
将式(19)代入到式(17),可得
工艺过程:将汉生胶分散在甘油里面,再倒入适量烧开的去离子水,搅拌均匀,加入B相剩余组分,加热搅拌至 85 ℃;混合A相并加热至85 ℃;混合A,B两相,均质5 min,并保温搅拌30 min;冷却至60 ℃加入C相(用少量水分散),继续冷却搅拌至45 ℃以下加入D相组分,继续搅拌冷却至室温。
(20)
其中
(21)
(22)
(23)
将式(20)代入到式(16),可得
(μ2A+μB+C)Q=0,
(24)
其中
(25)
(26)
(27)
μ=ω2.
(28)
取z=[μQTQT]T,则式(24)变换为
(29)
从式(29)容易看出,其中的系数矩阵是轴向波传播参数λx和周向波传播参数λθ的函数,均与圆频率ω无关.对于给定的轴向波传播参数λx和周向波传播参数λθ,点阵夹芯圆柱壳的频率求解转换为求解式(29)的广义特征值问题.另外,从式(29)还可以看出,本文方法的求解自由度规模为通常不大于一个胞元的自由度,不需要对整个点阵夹芯圆柱壳进行建模,且对胞元的具体构型没有特别要求,即胞元的结构矩阵可由现有的商业软件导出.
3 点阵夹芯圆柱壳中的波传播分析
根据结构中自由波的传播与自振模式的对应关系:当波传播参数取适当的值,使得波在结构中反射叠加后形成驻波时,结构达到了某一阶自振模式[27-28].圆柱壳自由振动涉及周向和轴向两个方向的波传播.首先考虑周向,考虑周期性边界条件,容易知道圆柱壳周向的波数为整数,则胞元在周向的波传播参数为
λθ=einθcell,n=0,±1,±2,…,
(30)
其中θcell为胞元在周向掠过的弧度.
其次考虑胞元轴向波传播参数的求解,本文利用自由波在梁中的传播分析来求解圆柱壳轴向的波传播参数.根据驻波形成的条件,波在轴向传播一个周期需要满足以下条件:
2kL+(φL+φR)=2mπ,m=0,±1,±2,…,
(31)
其中L为圆柱壳的长度,k为轴向半波数,φL为入射波和反射波在圆柱壳左端边界上的相位差,φR为入射波和反射波在圆柱壳右端边界上的相位差.对于简支边界条件,入射波和反射波的相位差为-π,对于固支或自由边界条件,入射波和反射波的相位差为-π/2[27-28].
将式(31)移项可得轴向半波数,进而轴向的波传播参数为
(32)
其中Lcell为胞元沿轴向的长度.
需要注意的是,根据文献[27-28],自由波在梁中传播的通解可以由4个分量叠加而成,分别为e-ikx,eikx,e-kx,ekx,其中k的正负号分别代表着波的传播方向.可以看出,前两个分量为传播波分量,后两个分量为近场波(near field wave),也称倏逝波(evanescent field wave).随着传播距离的增加,近场波呈指数衰减.考虑不同的边界条件,在两端简支的边界条件下,近场波为零[27-28];而在其他边界条件,如固支、自由边界条件等情况下,近场波不为零.然而,需要指出的是,由于近场波衰减很快,且频率越高,衰减越快,所以当频率较高、波数较大时,近场波的影响可以忽略不计.鉴于上述分析,本文方法在推导过程中没有考虑近场波的影响,故本文方法在两端简支边界条件下,具有较高的计算精度,而在其他非简支边界条件下,精度受近场波的影响:对于较低阶的自振频率,本文方法的计算精度较差;对于高阶自振频率的求解,波数的增加使得近场波影响变小,计算精度会越来越高.
最后,点阵夹芯圆柱壳的模态可以通过入射波和反射波叠加得到[27-28],例如,对于两端简支的点阵夹芯圆柱壳,其模态φ可以表示为
(33)
综上,本文方法求解点阵夹芯圆柱壳自振频率和模态的步骤如下:
① 根据式(30)和(32),求得点阵夹芯圆柱壳在轴向和周向的波传播参数λx和λθ;
② 将两个方向的波传播参数代入式(9),并结合式(25)—(27)可得式(29)中的系数矩阵A,B和C;
③ 求解式(29)的广义特征值问题即可得到广义特征值μ和广义特征向量z;
④ 结合广义特征值μ和式(28)即可得到自振频率ω,结合广义特征向量z、式(8)和(10)即可得到qe; ⑤ 将qe代入式(5)可以得到qi,进一步利用式(33)即可得到点阵夹芯圆柱壳的模态.
4 数 值 算 例
本节利用一个点阵夹芯圆柱壳来验证本文方法的正确性和高效性,其周向有300个胞元,轴向有250个胞元,如图2(a)所示.胞元为金字塔型,如图2(b)所示,其前后面板分别为半径为0.99 m和1.01 m的圆柱面,轴向长度均为20 mm,周向掠过的角度均为1.2°,厚度均为2 mm,四根连接梁的截面为圆形,连接梁半径为1 mm.胞元材料的质量密度为2 711 kg/m3,弹性模量为68.98 GPa,Poisson比为0.33.点阵夹芯圆柱壳两端的边界条件依次考虑为简支-简支(SS)、固支-固支(CC)、自由-自由(FF)、固支-简支(CS)和固支-自由(CF),分别利用本文方法和有限元方法对其进行自由振动分析.

(a) 点阵夹芯圆柱壳 (b) 金字塔型胞元 (a) A lattice core sandwich cylindrical shell(b) A pyramidal lattice truss core element图2 点阵夹芯圆柱壳及其胞元示意图
4.1 两端简支
首先考虑两端简支边界条件,胞元的上下面板均使用4个相同大小的壳单元建模,芯子中的4根连杆均使用3个梁单元建模,胞元有限元模型共有156个自由度;全尺寸有限元模型由胞元有限元模型在两个方向上阵列得到,共有7 207 200个自由度.
本文方法中使用的胞元刚度矩阵和质量矩阵从Nastran中导出,并使用MATLAB编写计算程序,使用CPU为8核*3.60 GHz,内存为32 GB的桌面级电脑,单核计算一个工况所花费时间大概为1 s.全尺寸有限元模型使用Nastran建模,计算在CPU为80核*2.3 GHz、内存为512 GB的高性能工作站上进行,使用18核计算一个工况(前100阶模态)所花费时间大概为40 min.需要指出的是,计算时间除了受计算规模、硬件配置影响以外,还受其他因素的影响,故此处两者的计算时间为多次计算时间取的平均值.以上的计算时间对比验证了本文方法的高效性.
表1给出了本文方法和全尺寸有限元模型计算得到的频率结果,由于本文重点关注圆柱壳的呼吸模态,所以表中没有给出周向波数为0或1对应的固有频率.可以看出,两端简支边界条件下,本文方法计算的点阵夹芯圆柱壳的固有频率与全尺寸有限元模型的结果吻合很好,验证了本文方法的有效性.

表1 两端简支边界条件下(SS)点阵夹芯圆柱壳的自由振动频率对比
图3给出了本文方法和有限元方法计算得到的点阵夹芯圆柱壳的模态形状(m=4,n=3)对比,可以看出两种方法计算的模态形状吻合较好.
4.2 其他边界条件
本小节考虑了其他边界条件下的点阵夹芯圆柱壳的自由振动问题,依次为固支-固支(CC)、自由-自由(FF)、固支-简支(CS)和固支-自由(CF).表2—5给出了上述4种边界条件下,本文方法和有限元方法计算得到的点阵夹芯圆柱壳的固有频率对比.从表中数据可以看出,在上述4种边界条件下,本文方法的计算结果与有限元方法的计算结果误差比在两端简支边界条件下的结果误差大,这是由上述4种边界条件下近场波的影响造成的.随着波数的增加近场波迅速衰减,其对结果的影响越来越小,表2—5中的误差数据验证了这一点.另外,从表中还可以看出,虽然本文方法在上述4种边界条件下的计算结果与有限元计算结果存在误差,但是误差大小整体在可接受范围内.
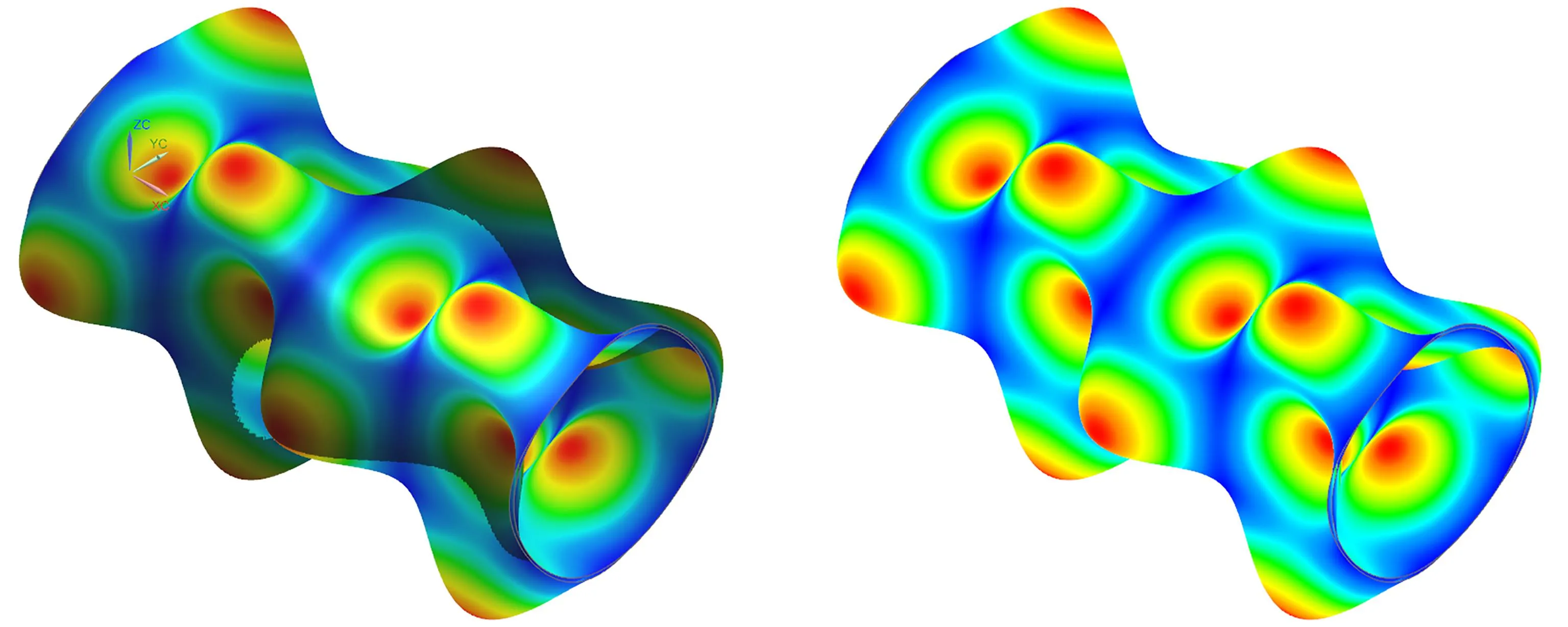
(a) 有限元方法 (b) 本文方法(a) The finite element method (b) The present method图3 本文方法和有限元方法计算的模态对比(m=4, n=3)
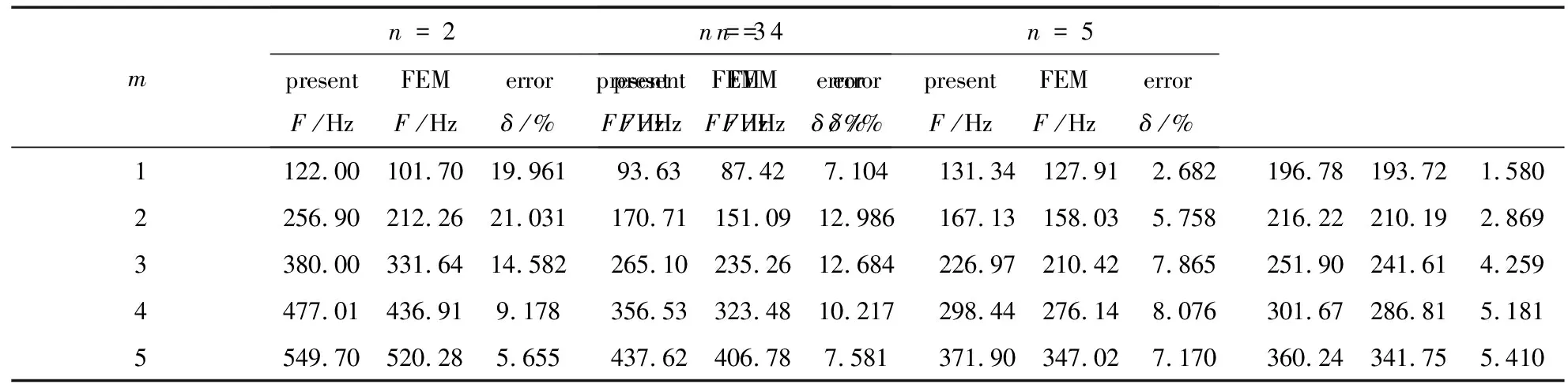
表2 两端固支边界条件下(CC)点阵夹芯圆柱壳的自由振动频率对比

表3 两端自由边界条件下(FF)点阵夹芯圆柱壳的自由振动频率对比

表4 一端固支一端简支边界条件下(CS)点阵夹芯圆柱壳的自由振动频率对比
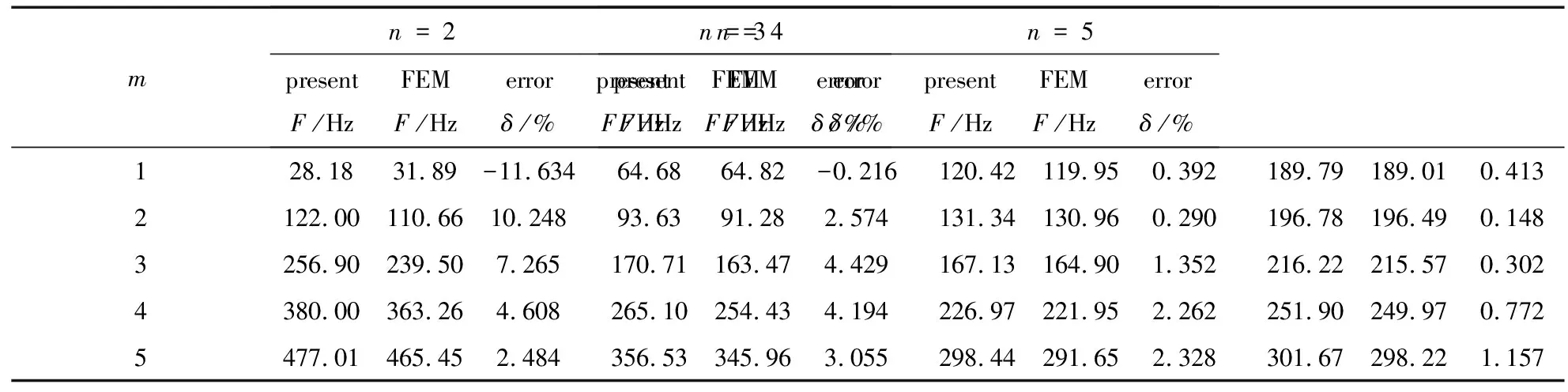
表5 一端固支一端自由边界条件下(CF)点阵夹芯圆柱壳的自由振动频率对比
5 结 论
本文针对点阵夹芯圆柱壳的自由振动分析发展了波有限元方法.首先,基于二维波有限元方法建立了点阵夹芯圆柱壳单个胞元的控制方程,该控制方程的自由度规模显著小于全尺寸有限元模型;然后,利用Neumann级数推导了约束刚度矩阵的显式表达式,使得控制方程中的频率分离出来,从而将固有频率求解转化为胞元的二次特征值问题;最后,考虑驻波的形成条件求得圆柱壳轴向和周向的参数,得到了点阵夹芯圆柱壳的固有频率.数值算例表明:本文方法对两端简支点阵夹芯圆柱壳的自由振动具有很高的预测精度,而对于其他边界条件,受近场波的影响预测精度略差,然而随着波数的增加,近场波快速衰减,本文方法的预测精度会越来越高.
致谢本文作者衷心感谢大连理工大学工业装备结构分析国家重点实验室开放课题(GZ21110)对本文的资助.

