空穴效应下泡沫金属复合相变材料热性能数值模拟

潘涵婷, 许 多, 徐洪涛, 罗祝清

(上海理工大学 能源与动力工程学院, 上海 200093)

0 引 言

人类社会的发展与能源密切相关,为解决能源紧缺及环境污染等问题,开发利用可再生能源已成为必由之路[1]．风能、太阳能等可再生能源不排放温室气体,对环境污染小,但均存在稳定性差及时间、空间分布不均的缺点[2],因此迫切需要发展储能技术．由于相变材料(phase change material,PCM)具有较高的储能密度和在近乎恒定温度下释放或吸收热量的特性,从根本上平衡了能量供需之间的矛盾[3]．目前,利用PCM来进行潜热储能被广泛应用于太阳能发电系统[4]、余热利用[5]、电池热管理系统[6]、航天航空仪器恒温及动力供应[7]等领域．

然而传统PCM普遍存在导热率低的问题,填充泡沫金属骨架是当前一种有效的解决方案[8-9]．Huang等[10]通过研究泡沫金属复合PCM的传热性能,发现其在较高的孔隙率下能够加快PCM的熔化速度．Yang等[11]利用蓄放热实验研究了纳米颗粒与泡沫金属对不同PCM传热性能的影响,研究结果表明泡沫金属在缩短凝固及熔化时间上比纳米颗粒更具优势．马预谱等[12]研究发现在储能密度方面,泡沫金属铜的性能优于铝翅片．上述文献都表明了泡沫金属骨架对于相变传热的增益作用．

此外,PCM会在相变过程中重复收缩膨胀,产生局部压力,导致在内部空间产生充满气体的空穴,从而引发热应力集中分布,对PCM的使用寿命造成损伤[13-14]．Chiew等[15]通过实验研究了两种PCM储能系统(100%的PCM与带有20%空穴的PCM),研究表明空穴的作用类似绝热层,明显削弱了系统的储热性能．Janghel等[16]提出了考虑空穴存在的半解析模型,分析了其在PCM凝固过程中的影响,结果表明形成于冷壁上的空穴会降低凝固速度,使凝固时间变长．Solomon等[17]分析了内部空穴位置对相变胶囊储能性能的影响,发现当空穴集中分布于胶囊中心时,PCM的完全熔化时间最短,相比于随机分布及集中顶部的情况,分别快22%与39%．Li等[18]分析了微重力条件下复合PCM中空穴体积分数对储能性能的影响,研究发现仅在热传导作用下,近壁空穴和随机分布空穴的储能量均随空穴体积分数的增加而减小．

由于泡沫金属的复杂结构,针对复合PCM熔化过程中的空穴问题研究尚少,并未明确其传热机理．此外,模拟工作大多采用二维模型,忽略了泡沫金属骨架的三维效应．本文通过构建三维复合PCM模型,克服了二维泡沫金属骨架导热性不连通的问题．同时,为模拟相变过程中存在的空穴效应,本文提出了一种随机分布的空穴结构．基于焓法的多松弛时间格子Boltzmann方法(multiple-relaxation time lattice Boltzmann method,MRT-LBM),对于处理复杂固液相变界面运动及边界条件有着很大优势[19-20],且依靠高性能计算显卡(GPU)大幅减少模拟计算时间成本[21]．

因此,本文采用GPU加速MRT-LBM,基于泡沫金属骨架强化传热下的复合PCM,对不同空穴体积分数、空穴分布位置及骨架导热系数比下的瞬态熔化过程进行数值模拟,进而探究随机分布空穴对于复合PCM熔化性能的影响效应．

1 物理与数学模型

1．1 物理模型

泡沫金属结构是由骨架和孔隙空间组成,如图1(a)所示．结合实际骨架结构,本文首先建立了三维复合PCM模型(孔隙率为0.956),如图1(b)所示．图1(c)为在此模型基础上构建了随机分布空穴结构, 方腔的L∶W∶H为2∶1∶2,左壁面设置为高温面, 其余面为绝热面, 其中, 球形空穴尺寸为方腔长度L的1/35．图 1(d)—1(g)为4种不同空穴分布位置模型,同时固定空穴的体积分数为3%,其中方腔内空白部分均填充PCM,深蓝色网状结构代表泡沫金属骨架模型,灰色球体代表空穴．

(a) 实际泡沫金属结构 (b) 泡沫金属骨架模型(c) 随机分布空穴模型 (a) The actual metal foam structure (b) The metal foam skeleton model (c) The randomly distributed cavity model

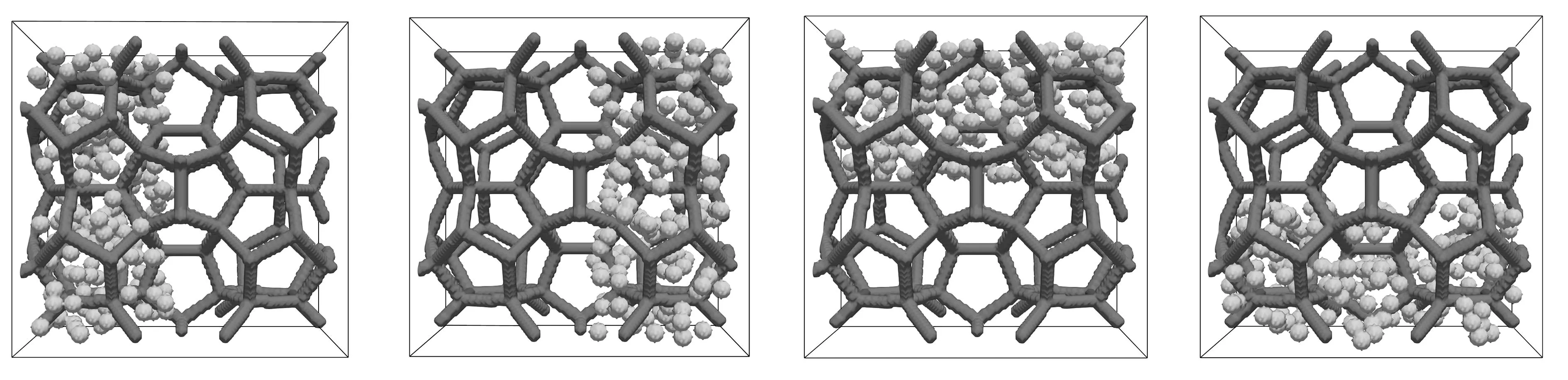
(d) 靠近热壁面侧空穴 (e) 远离热壁面侧空穴(f) 上半侧空穴(g) 下半侧空穴(d) Cavities near the hot wall side (e) Cavities away from the hot wall side (f) Cavities on the upper side (g) Cavities on the lower side图1 三维模型介绍

1．2 数学模型

复合PCM的相变过程采用了以下假设：

① 根据Boussinesq假设,PCM被认为层流、不可压缩的;

② 除了导热率,PCM的液体和固体热物性可认为是一致的;

③ 忽略空穴内的相变问题,同时它们的位置和形状不随时间改变．

空穴体积分数ξ被定义为

(1)

式中,Vc和Vd分别表示空穴和矩形腔所占网格数．

PCM各阶段的导热系数λPCM、温度T和液体分数fl通过以下公式计算：

(2)

(3)

(4)

式中,Tm表示相变温度,K;cp表示比热容,J·kg-1·K-1;下标s和l分别表示固态和液态．

PCM、泡沫金属和空穴的焓的定义式如下：

hf=cpf(T-Tm)+flLa,

(5)

hw=cpw(T-Tm),

(6)

hv=cpv(T-Tm),

(7)

式中,La表示潜热,kJ·kg-1;下标f、w和v分别表示PCM、泡沫金属和空穴．

本文涉及4个无量纲参数：Stefan数Ste,Prandtl数Pr,Rayleigh数Ra和Fourier数Fo的定义式如下：

(8)

式中,Th为热壁面温度, K;υf为流体的运动黏度, m2/s;αf为流体的热扩散系数, m2/s;g为重力加速度, m/s2;β为热膨胀系数, K-1;L为特征长度, m．

本文在Pr=1,Ste=0.4,Ra=25 000,λs/λl=1.3,λv/λl=0.1的工况下进行模拟．

矩形腔的初始和边界条件设定如下：

(9)

式中,u,v,w分别为x,y,z方向上的无量纲速度分量．

2 格子Boltzmann方法

2．1 流体流动

本文采用D3Q19模型,同时选用Huang等[22]提出的浸入式移动边界方法,其分布函数fi的演化方程为

(10)

式中,x为粒子的坐标位置,Δt为时间步长．

(11)

式中,ωi,ei和cs分别为权重系数、离散速度和格子声速．

外力项Fi定义为

(12)

式中,浮力项fb=ρfβg(T-Tm)．

权重函数B的表达式为

(13)

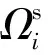
(14)

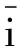
基于以上算式,宏观速度u可通过如下公式计算：

(15)

2．2 固液相变

本文采用Li等[23]提出的基于焓法的D3Q7 MRT模型,焓分布函数gi表达式为

gi(x+eiΔt,t+Δt)=gi(x,t)-M-1S[m(x,t)-meq(x,t)]．

(16)

碰撞过程实现形式为

m(x,t+Δt)=m(x,t)-S[m(x,t)-meq(x,t)]．

(17)

平衡态分布函数meq定义为

(18)

式中,ωT=0.25．

转换矩阵M和松弛矩阵S为

(19)

S=diag(s1,s2,s3,s4,s5,s6,s7),

(20)

式中,s1=1,s2=s3=s4=1/τ,s5=s6=s7=2-1/τ,松弛时间τ的定义式为

(21)

焓值h通过如下计算式得出：

(22)

3 网格无关性验证及模型验证

为验证复合PCM的传热过程和熔化过程,首先对正二十烷(Z<0)与金属铜(Z>0)界面之间的一维耦合传热过程进行验证,其耦合传热模型图如图2(a)所示．图2(b)展示了在无量纲位置坐标Z方向上两种物质的温度分布曲线图,可以发现LBM模拟结果与解析解[24]吻合良好,验证了LBM实现耦合传热过程的准确性．其次,为了准确模拟PCM的相变熔化过程,对两组工况下(case 1：Ra=25 000,Pr=0.02,Ste=0.1; case 2：Ra=25 000,Pr=10,Ste=0.1)的瞬态熔化过程进行了模拟．PCM熔化过程中的平均液化率和热壁面Nusselt数曲线如图3所示,这与Li等[23]的结果吻合良好．

最后,基于相同的模拟工况,对填充金属骨架的复合PCM的熔化过程进行了网格独立性验证．图4显示了不同网格数下,随无量纲时间Fo变化的fl,ave及Nuave,可以发现不同网格数下的差异非常小, 最大误差为0.82%．基于模型结构的复杂性和计算成本的控制,采用140×70×140网格数进行后续的工作．

(a) 耦合传热模型图 (b) 耦合传热验证 (a) Diagram of the coupled heat transfer model (b) Verification of the coupled heat transfer图2 界面耦合传热验证

(a) 平均液化率fl,ave (b) 热壁面平均Nusselt数Nuave(a) The average liquid fraction fl,ave (b) The average Nusselt number Nuave图3 三维固液相变验证

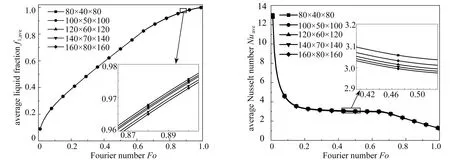
(a) 平均液化率fl,ave (b) 热壁面平均Nusselt数Nuave(a) The average liquid fraction fl,ave (b) The average Nusselt number Nuave图4 网格无关性验证

4 结果与讨论

4．1 不同空穴体积分数下复合PCM的热性能

为探究空穴耦合作用下复合PCM的热性能,对三种不同空穴体积分数(ξ=0%,2.4%和7.6%)下的整体及截面温度云图进行了对比分析,如图5所示．其中,黑色部分表示泡沫金属骨架结构,白色球体表示空穴结构．当Fo从0.15变化到0.40时,可以发现PCM熔化量增多,固液相界面开始向上弯曲,这是因为在浮升力的驱动作用下,液体PCM向上流动,增加了上半部分PCM之间的热传递．

此外,随着ξ的增加,熔化界面的弯曲程度降低,越趋近于平行热壁面,这是因为空穴的存在抑制了自然对流作用．在y=35(中间)处的截面图中可以观察到,空穴附近的等温线比金属骨架附近的等温线更密集,这说明了空穴限制了PCM内部的热量传递,同时空穴在矩形腔内分布的位置也会左右其传热特性．

图5 矩形腔整体及截面处温度分布图

为定量研究复合PCM的热性能,引入熔化参考比X来评价空穴效应,其定义式如下：

(23)

式中,ξi,fl,ave表示不同ξ下空穴的fl,ave,ξ0,fl,ave表示无空穴情况下的fl,ave．

图6(a)为不同ξ下的熔化参考比X曲线．依据曲线趋势,将整个过程划分为三个熔化区域．以ξ=7.6%为例,在阶段Ⅰ,由于空穴的存在减少了PCM的总量,同时在熔化前期大部分随机分布的空穴尚处于固体PCM中,因此空穴效应还未显著影响PCM的熔化过程,所以出现X值大于0的情况．在阶段Ⅱ,X值从0减小到最小值,随着熔化过程的推进,更多的PCM开始熔化,致使更多的空穴存在于液体PCM中,这将阻碍PCM的熔化过程,因此X值一直小于0．此现象可以由以下两个原因来解释：首先,空穴低热导率的特性增加了过程的传热热阻;其次,空穴的存在增加了自然对流过程中的流动阻力．在阶段Ⅲ,X值从最小值变化到0,熔化过程进入末期,无空穴的PCM最先完全熔化,因此X值开始接近于0,最终达到稳定．

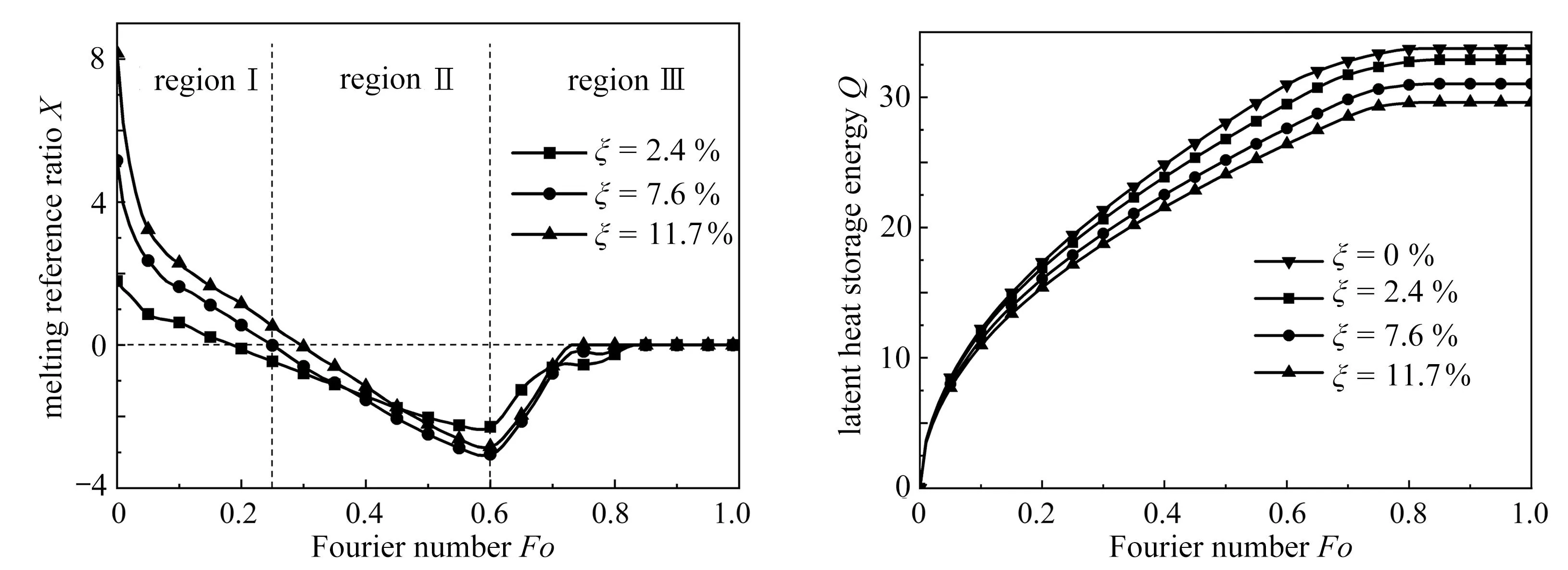
(a) 熔化参考比X (b) 潜热储能量Q(a) The melting reference ratio X (b) The latent heat storage energy Q图6 不同ξ下复合PCM的熔化参考比X和潜热储能量Q

图6(b)为不同ξ下潜热储能量Q的变化曲线图,可以观察到空穴的存在显著降低了PCM的储热能力．在Fourier数Fo=0.7时刻下, 当ξ=2.4%,7.6%和11.7%时, 相较于无空穴情况下的Q分别减少了3.2%,9.0%和13.0%．这极大地影响了储热容器的储热能力,因此控制储能单元中空穴的形成对提高储热效率至关重要．

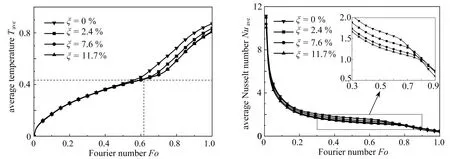
(a) 平均温度Tave (b) 热壁面平均Nusselt数Nuave(a) The average temperature Tave (b) The average Nusselt number Nuave图7 不同ξ下复合PCM平均温度和热壁面平均Nusselt数

图7(a)为随时间变化的不同ξ下复合PCM的平均温度．在Fo=0.6之前,温度变化比较缓慢,且有无空穴对复合PCM的平均温度没有明显的影响．当Fo>0.6时,不同ξ下复合PCM内的平均温度出现明显差异,无空穴时的平均温度最高,且随着ξ的增加,平均温度降低．这是因为大部分空穴处于液体PCM中,增加了传热热阻,同时温度差异在显热升温时表现更加明显．

图7(b)为不同ξ情况下热壁面平均Nusselt数Nuave的变化趋势．熔化起始阶段,液体层厚度很小,温度梯度很大,Nuave数值较高．随着熔化过程的进行,Nuave逐渐下降并趋于稳定值,同时随着空穴数量的增加,Nuave值越小,表明空穴的存在增加了对流的阻碍作用,从而抑制了流动．在熔化后期,随着PCM内部温差逐渐减小,熔化界面因接触到右壁面而面积减小,Nuave显著下降,并趋于0．

4．2 不同空穴位置下复合PCM的热性能

根据4.1小节的介绍可以知道空穴位置对PCM熔化过程有着至关重要的影响．因此本小节讨论了四种不同空穴位置分布下复合PCM的热性能,且ξ=3.0%．图8为不同空穴位置排布下的温度分布图,可以观察到在PCM熔化过程中,在无空穴存在时等温线相对平整,而有空穴存在时等温线开始变得密集,且向空穴方向收缩,这说明热量传递的速率减缓．在Fo=0.40时,发现随着更多的空穴暴露在液体PCM中时,PCM的熔化界面移动变缓．当空穴集中在远离热壁面侧时,PCM的熔化界面移动得最快,因为热量从左侧开始向右侧移动,左侧PCM中热量传递并未受到空穴的抑制作用．当空穴集中于靠近热壁面侧时,等温线分布最密集,这对热壁面传递热量是最不利的．

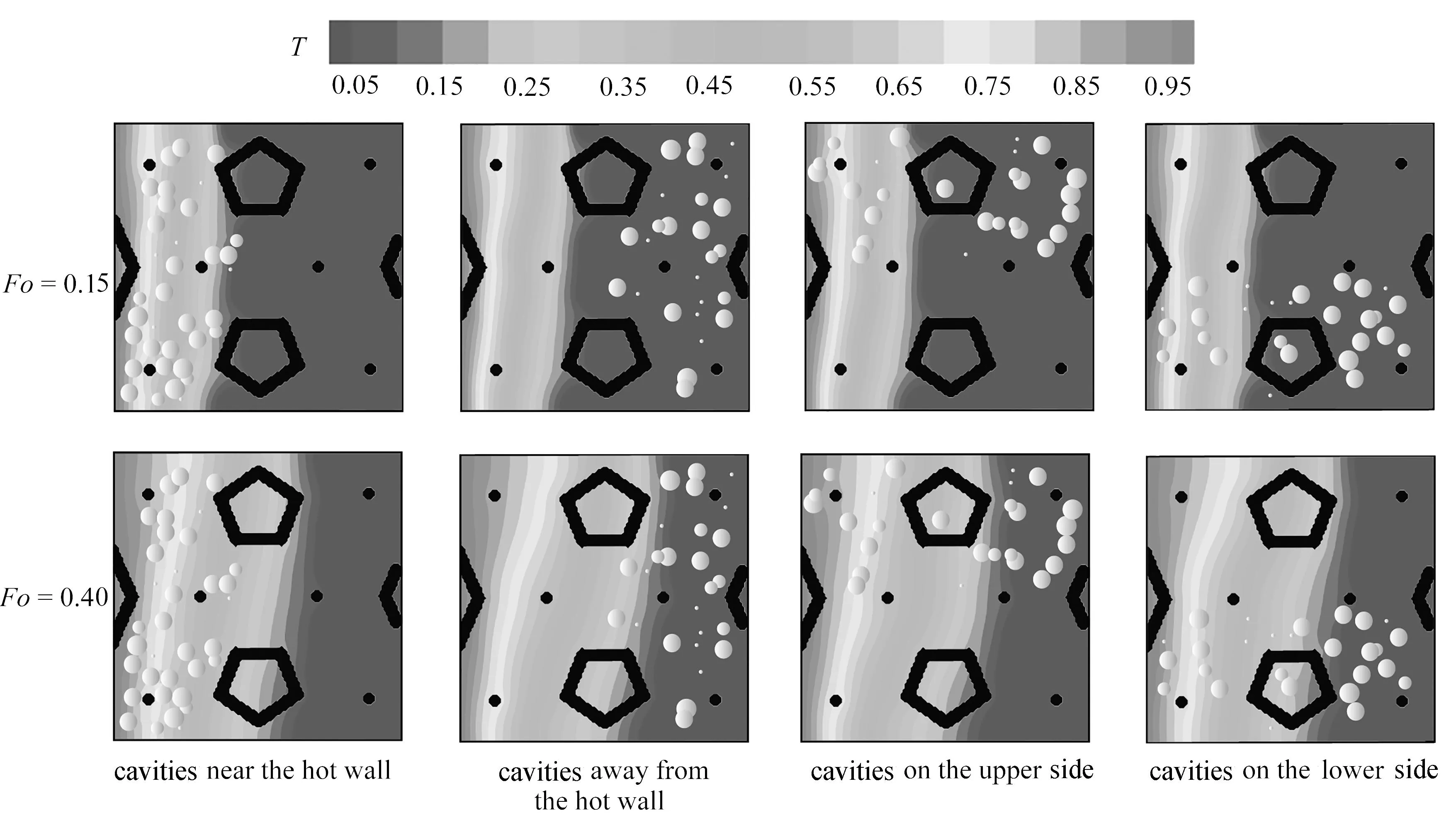
图8 不同空穴分布位置下的截面y=35处的温度分布图(ξ=3%)

图9(a)对具有不同空穴位置的PCM的熔化参考比X进行了比较．可以发现当空穴远离热壁面侧时,X曲线先保持不变,说明在这段时间内,空穴效应并未影响PCM内部的熔化过程．由于PCM总量的减少,且远离热壁面侧的空穴对流动过程的阻碍作用较小,使得X值一直大于0．而空穴靠近热壁面侧情况下,曲线处于X=0的下方,这是因为空穴的低导热率对PCM内部传热的阻碍作用以及对流体流动的抑制效果,充当了绝热层,削弱了传热过程．而空穴集中在上、下半侧时,其作用于熔化的影响相对较小．

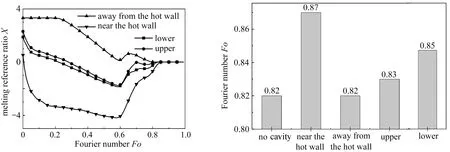
(a) 熔化参考比X (b) 完全熔化时间 (a) The melting reference ratio X (b) The total melting time图9 不同空穴分布位置下复合PCM的熔化参考比X和完全熔化时间

图9(b)为不同空穴位置情况下复合PCM的完全熔化时间,无空穴时为Fo=0.82,当空穴存在时,都在一定程度上延长了熔化时间．可以发现当空穴靠近热壁面侧时,对复合PCM熔化速率的延缓效果最强烈,使其完全熔化时间增加了6.1%．当空穴远离热壁面侧时,它的阻碍作用最小．值得关注的是,当空穴位于上半侧时的复合PCM完全熔化时间小于其位于下半侧时的情况,这是因为在热浮升力的影响下,方腔上侧PCM的熔化速率快于下侧PCM,且当空穴集中在下半侧时,这使得下半侧PCM的传热速度进一步减慢．

4．3 不同泡沫金属导热系数比下复合PCM的热性能

泡沫金属与PCM之间的导热作用不仅决定了传热速率,同样也会影响空穴的耦合效应．图10(a)为不同ks下复合PCM的熔化参考比曲线图(ξ=7.6%),随着ks减小,X曲线的波动范围越大,说明空穴效应越显著．当ks=250和500时,X值一直大于0,说明空穴效应在高导热系数比的情况下可以忽略,这得益于泡沫金属与PCM间的传热主导地位,削弱了空穴带来的抑制效果．

图10(b)对比了不同ks情况下复合PCM的全熔时间．当ks=20时,有无空穴下的差异最为明显,无空穴时PCM的全熔时刻为Fo=1.01;而当存在空穴时,全熔时刻为Fo=1.12,无量纲熔化时间增加了10.9%．随着ks的进一步增加,空穴效应的影响逐渐减小,当ks=50时,有空穴情况下PCM的熔化时间比无空穴情况仅增加了2.4%．然后,当ks进一步增大到100,250和500时,存在空穴情况下的无量纲熔化时间均比无空穴情况下降了0.1．因此,可以合理推断当采用导热系数比大于100时,存在空穴的复合PCM的熔化时间小于无空穴情况,可有效缓解空穴带来的负面效应．

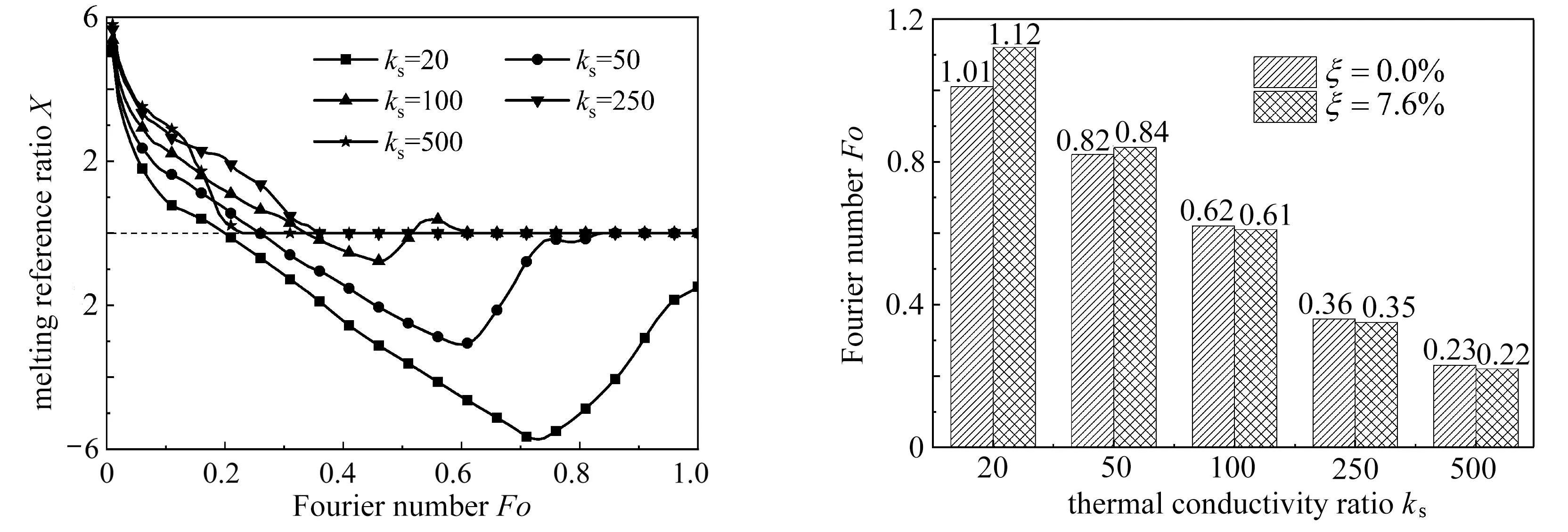
(a) 熔化参考比X (b) 完全熔化时间(a) The melting reference ratio X (b) The total melting time图10 不同ks下复合PCM的熔化参考比X和完全熔化时间

5 结 论

本文建立了耦合空穴的泡沫金属复合PCM模型,基于焓法的三维MRT-LBM模拟了不同空穴体积分数ξ、位置分布以及导热系数比ks对复合PCM热性能的影响,对温度云图、熔化参考比和完全熔化时间等因素进行了数值分析,得出了以下结论：

1) 空穴主要通过增加传热热阻和阻碍流体流动两方面来抑制复合PCM的传热过程．空穴的存在不仅使PCM内部的等温线分布更加扭曲,同时降低PCM的潜热储热量．在Fourier数Fo=0.7时刻下,当ξ=2.4%,7.6%和11.7%时,相较于无空穴情况下的储热量分别减少了3.2%,9.0%和13.0%．

2) 当空穴靠近热壁面侧时,其对复合PCM熔化过程的抑制作用最为明显,这时的空穴类似于绝热层．而空穴位于热壁面侧较远时对复合PCM的熔化过程影响最小,因此在实际工程中,当空穴无法避免时,尽可能使空穴远离热壁面侧．

3) 相较于无空穴情况,当复合PCM中存在ξ=7.6%的空穴时,选用ks=20的泡沫金属时,其全熔时间增加了10.9%．随着泡沫金属和PCM的导热比的进一步增大,空穴效应被弱化．为削弱空穴效应,可以选择导热系数比超过100的泡沫金属骨架来强化热传导．