非均匀磁场下Maxwell磁纳米流体的拉伸流动与磁扩散分析

吴学珂, 刘春燕, 白 羽, 张 艳

(1. 北京建筑大学 理学院, 北京 100044;2. 建筑结构与环境修复功能材料北京市重点实验室, 北京 100044)

0 引 言

聚合物是经聚合反应生成的高分子化合物,而熔融的聚合物在力的作用下可以流动,是一类同时具有黏性和弹性的黏弹性流体[1]．在聚合物中加入纳米颗粒可有效改善聚合物的性能,提高其韧性和传热速率,在工业和生物医学等领域被广泛应用,增加了能源的利用率[2-3]．磁性纳米颗粒具有磁性特征且具有纳米颗粒的独特效应,常见的磁性纳米颗粒有金属铁、钴、镍、金属氧化物Fe2O3和Fe3O4等,在熔融聚合物中加入微量的磁性纳米颗粒,可以使材料的各种性能如导电性、导热性、阻隔性等提高．Zainal等[4]应用边界层理论研究了包含电磁流体动力学在拉伸板上复合纳米流体的非稳态常驻点流动．Sheikholeslami等[5]研究了非均匀磁场对Fe3O4-水基纳米流体强制对流换热的影响．

对磁性纳米流体施加外磁场,可以在非接触的条件下对其流动产生影响．这种非接触操控方式在实际操作中更便于实现,且操控范围广,不受pH值、离子强度、表面电荷和温度的影响[6]．在多数实际情况下,外加磁场是可变的,近年来,很多研究探讨了非均匀磁场对纳米流体流动的影响．Sheikholeslami等[7]研究了变磁场下磁场力对纳米流体传热的影响．Shaker等[8]研究了非均匀磁场对磁性纳米流体在开腔通道内混合对流换热的影响,发现腔加热壁的上角附近产生了涡流．磁流体力学(MHD)是结合经典流体力学和电动力学的方法研究导电流体和磁场相互作用的学科[9],在天体物理、地球物理、宇航工程、电磁学以及工程技术中都有广泛的应用．Bég等[10]研究了导电金属流体在感应磁场作用下的流动,发现增加磁参数会使速度提高、感应磁场降低．Hayat等[11]采用有限差分格式数值计算了随时间变化的黏性纳米流体在感应磁场中的流动, 并讨论了Brown运动和热泳运动．但在现有的关于非均匀磁场的数值模拟研究中, 尚未清楚阐明感应磁场的物理机制．

考虑到黏弹性磁纳米流体在流动过程中的复杂特性[12],将分数阶导数引入本构关系能更灵活地描述黏弹性流体的性质．杨旭等[13]基于分数阶微积分理论,采用空间分数阶导数建立了圆管内分数阶非Newton流体本构模型,为非Newton流体的记忆特征提供了一种建模方法．Zhao等[14]通过在本构关系中引入分数阶Maxwell剪切应力和Cattaneo热流模型,研究了Maxwell流体在平面上的非稳态Marangoni对流换热．然而上述模型中分数阶导数参数固定,导致了有限的记忆特性和非局部特性,且无法准确描述一些复杂的动力学过程,例如复合材料的流变特性[15]．分布阶本构模型是分数阶导数在参数值范围内的积分,具有不同的时间和空间特征[16],作为更有效的工具引起了很多学者的关注．Yang等[17]建立了空间分布阶本构关系来研究边界层中的流动和传热．Long等[18]基于Maxwell流体流动和Cattaneo传热的传统本构关系,建立了分布阶导数的非稳态Marangoni对流边界层流动和传热模型．Liu等[19]将分布阶导数引入Maxwell流体的本构模型,并分析了相关参数的影响．

基于上述研究发现,在感应磁场作用下,非稳态时间分布阶的Maxwell磁纳米流体流动的问题很少有人研究．本文将时间分布阶Maxwell本构关系代入动量方程,并与磁扩散方程建立流动和感应磁场的控制方程,然后结合有限差分方法与L1算法获得控制方程的数值解,最后分析相关参数对流动和感应磁场的影响．

1 数 学 模 型

时间分布阶Maxwell流体的本构方程为

(1)

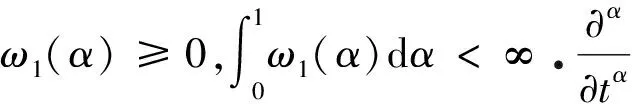
其中,Γ(·)为Gamma函数．

考虑线性拉伸板上的二维不可压缩非稳态Maxwell磁纳米流体的边界层流动问题,如图1所示．建立二维直角坐标系,其中x轴与平板平行,y轴垂直于平板．施加非均匀磁场He=H0(cos(x/L)+1),假设(u,v)和(H1,H2)分别是沿着板和垂直于板的速度和感应磁场的分量,并假设感应磁场的法向分量H2在壁处消失、平行分量H1在边界层边缘接近给定值．则时间分布阶Maxwell磁纳米流体的边界层流动和磁扩散控制方程为

(2)

(3)

(4)

满足下列初始条件和边界条件：

(5)

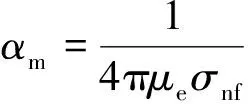
图1 物理模型示意图

纳米流体的物理性质参数为

(6)

其中φ是磁性纳米颗粒的体积分数,μf是流体的黏度,ρf和ρs分别是流体和磁性纳米颗粒的密度,σf和σs分别是流体和磁性纳米颗粒的电阻率．磁性纳米颗粒铁、钴、Fe2O3和Fe3O4主要的物理性质如表1所示[21-22]．

表1 磁性纳米颗粒的物理性质

对方程(2)—(5)进行无量纲化：

(7)

其中M是磁参数,Pr是磁Prandtl数,Re是Reynolds数,得到无量纲控制方程如下(为了方便,后面将省略标记“*”)：

(8)

(9)

(10)

无量纲化后的初值和边界条件为

(11)

因此,建立了二维非稳态Maxwell磁纳米流体的控制方程(8)—(11),方程(11)为相应的初始条件和边界条件．

2 数值差分格式

采用有限差分法与L1算法[23]相结合来求解耦合的二维分布阶控制方程(8)—(11)．对时间和空间进行网格划分,设hx,hy分别为沿x轴和y轴的空间步长,τ为时间步长．定义

其中Mx,My,N是网格划分的数量．

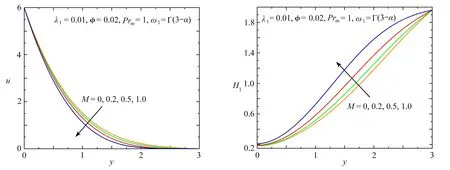
定理1 设0

称之为L1算法,其基本思想是将被积函数中出现的f的分数阶导数直接用数值微分公式逼近,还可改写为

(12)

其中cj=(j+1)1-α-j1-α,j=0,1,2,…,N．

根据中点Gauss求积规则,使用多个分数项的加权和变换时间分布阶分数导数,可以获得分布项的数值离散格式：

(13)

对于离散区域[0,1]中αr阶的时间分数阶导数,利用定理1中的L1数值离散格式(13),可得到

(14)

(15)

其中

cr,0=1,cr,s=(s+1)1-αr-s1-αr,s=0,1,…,N．

将离散格式(12)、(14)和(15)代入控制方程(8)—(10)和初边值条件(11),得到求解问题的数值差分格式．

3 结 果 分 析

利用第2节中的有限差分方法得到动量方程和磁扩散方程的数值解,并说明相关参数对速度和感应磁场的影响．构造解析解验证了差分格式的收敛性,如图2所示．

图2 数值解和解析解的比较

图3和图4描绘了磁性纳米颗粒Fe2O3、Fe3O4、Fe和Co对速度和感应磁场的影响．从图3可以看出,密度相近的Fe2O3和Fe3O4纳米颗粒对速度的影响几乎相同,而密度最大的Co使流速受到最大限制,速度边界层厚度最薄．从物理角度看,当磁性纳米颗粒的体积分数相同时,密度越大,颗粒间的间隙越小,从而阻碍了流体的运动．图4表明,添加的Fe2O3纳米颗粒电阻率最小,则感应磁场最大,磁边界层厚度最厚;对于电阻率相近的Fe和Co,感应磁场的分布几乎相同．由于磁性纳米颗粒的电阻率与电导率呈反比,所以当电阻率增大时,感应磁场减小．

图5和图6为变化的磁参数M对Fe3O4纳米流体速度和感应磁场的影响．图5中的曲线表明流动的模式一致,流速值随着磁参数的增加而降低．在非均匀磁场作用下,边界层内产生与流体运动方向相反的磁场力,所以当M>0时,磁场力对流体的速度起抑制作用,使得边界层厚度变薄．当M=0时,无磁场力,Fe3O4纳米流体速度由于内摩擦阻力作用逐渐减小．如图6所示,在边界层内感应磁场随M的增大而增大．因为M增大时磁导率增加,磁扩散效应显著,从而感应磁场增加．

图3 不同磁性纳米颗粒对速度的影响

图5 不同M对速度的影响

图7和图8显示了速度和感应磁场随磁性纳米颗粒Fe3O4体积分数φ的变化．当φ增加时,速度增大,边界层厚度变厚,感应磁场减小．由于拉伸板的运动导致固体颗粒运动增加,从而速度随着磁纳米颗粒的加入而增加．而在外加磁场的作用下,随着φ的增加,速度的增大导致磁对流项增大,使得磁扩散效应减小,从而在边界层内感应磁场减小．图9和图10显示了松弛时间参数λ1对Fe3O4纳米流体中速度和感应磁场的影响．当选择权重系数ω1(α) =Γ(3-α),无量纲时间t=1时,可以观察到λ1越大,速度和感应磁场越小,这是由于流体的黏性增加,阻碍了流体的运动进而导致磁场减小,这和应力松弛现象是一致的．

图7 不同φ对速度的影响

图9 不同λ1对速度的影响

4 结 论

磁性纳米颗粒可以改善聚合物的性能,线性拉伸板上非稳态流动与磁扩散的研究为其提供了良好的理论基础．本文利用分布阶本构模型,研究了黏弹性基磁纳米流体在非均匀磁场下的二维不可压缩边界层流动,并考虑了高Reynolds数下的感应磁场分布．将时间分布阶Maxwell方程引入动量方程,建立了速度和磁扩散控制方程组．使用有限差分法和L1算法耦合求解偏微分方程组的数值解,并验证了收敛性,结合图像分析了相关物理参数对速度和感应磁场的影响．所得主要结论如下：Maxwell流体的速度和感应磁场在添加Fe2O3纳米颗粒时达到最大,此时速度边界层和磁边界层的厚度最厚;由于磁场力的影响,增大的磁参数阻碍了流体的运动,增强了磁扩散;随着Fe3O4纳米流体体积分数增加,速度增大,感应磁场减小;此外,较高的松弛时间参数会使Maxwell流体的流动和磁场的扩散减弱．因此,本文从数值解的角度研究了添加磁性纳米颗粒的熔融聚合物在非均匀磁场下的边界层拉伸流动与磁扩散,对制备出高性能的聚合物材料具有重要意义．

致谢本文作者衷心感谢北京建筑大学金字塔人才培养工程项目(JDYC20220829)、北京建筑大学促进高校内涵发展定额项目(X21027)和北京建筑大学研究生创新项目(PG2023144)对本文的资助．