带有指数变换效应的复发事件数据的半参数估计*

张思琪,韦程东,何国源

(南宁师范大学 数学与统计学院,广西 南宁 530100)

某一事件随着时间的推移而重复发生的过程称为复发事件过程,这种过程提供的数据称为复发事件数据.复发事件数据广泛出现在医药公共卫生、工商业、社会科学和保险等领域,如呼吸病患者的哮喘发作、新型冠状病毒肺炎的重复感染、抑郁症患者的再次发作、肝癌肝移植术后复发、同一片区域多次发生地震、重要路段交通事故重复出现等[1].

对于复发事件数据,学者们根据协变量对复发事件过程的影响建立不同的模型,主要有两类.一类是强度模型,针对危险率函数和强度函数,将死亡事件作为复发事件的删失进行处理,但并未明显区分复发事件和终止事件.另一类是基于边际均值或边际比率模型,不再将终止事件看作独立删失,将终止事件与复发事件联系起来.例如Lin等[1]在不考虑历史条件的情况下研究了计数过程的比例均值和比率模型,该模型与强度模型相比更为稳健.对于带终止事件的复发事件数据,一般采用边际模型方法和随机效应模型方法来处理.

边际模型方法主要研究复发事件和终止事件的边际模型,不考虑两者之间的相关性,如Ghosh[3]通过一个任意计数过程的模型,提出协变量改变基线速率函数的时间尺度的加速速率模型.随机效应模型借助潜变量刻画复发事件和终止事件的相关性,并假设在给定脆弱变量时复发事件与终止事件独立,如Wang等[4]通过潜在变量的非平稳泊松过程对复发事件的发生进行模拟,将乘法强度模型扩展到半参数回归模型,提出了估算乘法强度下累积速率函数和回归参数的估算程序.然而在某些情况下,复发事件的终止时间可能与复发事件的过程相关,不符合独立删失的假设,这时就需要考虑复发事件过程和失效时间联合建模.如Huang等[5]使用共同的潜在变量对复发事件过程的强度和失效时间危险之间的关联进行建模,提出“borrow-strength”估计方法,从复发事件数据中估计潜在变量的值.戴家佳等[6]对带有终止事件的复发事件数据,提出了加性加速比率回归模型,运用广义估计方程的思想给出了参数的估计.Huang等[7]提出一种既不依赖于脆弱变量的分布,也不依赖于失效时间的一种半参数估计方法,允许协变量将删失时间与复发事件联系在一起,这种方法虽然很灵活,但它是基于复发事件过程的泊松分布的,在某些方面无法应用.因此Kalbfleisch等[8]在完全没有泊松过程假设的情况下进行参数估计,所得结果具有极大的稳健性,其中的共享脆弱性的估计仅与复发事件过程和终止事件过程之间的关联有关.Xu等[9]用共享脆弱性变量对复发事件和失效时间建立联合尺度变换模型,不需对复发事件过程进行泊松假设,回归参数具有边际解释.Xu等[10]提出了一种既不需要脆弱性分布的参数假设,也不需要重复事件过程的泊松假设估计模型参数.在处理复发事件数据时,复发事件的均值函数比风险函数具有更强的解释能力[11].据文献所知,目前还未有学者研究协变量对于复发事件过程的改变时间指数的尺度效应.本文所提出的模型与文献[5]中考虑的联合模型相比,并未对给定Z的N(t)条件分布施加泊松型假设.本文的复发事件模型与文献[10]中提出的模型相比,共同点是均包含两种类型的协变效应,不同之处是本文中模型的协变效应是改变时间指数尺度效应和改变风险的乘法变化效应.

本文提出一种带有指数变换效应的半参数估计,放宽了应用条件,无需对复发事件过程进行泊松假设,不需要了解未观察到的脆弱变量的信息,在适当的正则条件下,建立了估计量的相合性和渐近正态性.估计程序使用MATLAB,数值模拟结果表明本文提出的估计量几乎是无偏的,真实值与估计值曲线拟合度高.因此本文提出的半参数模型是有效的.

1 模型建立

设[0,τ]是观察复发事件发生的时间段,N(t)为时间区间[0,t]内复发事件发生的次数.将删失时间Y定义为Y=C∧D,∧表示最小值,C为非信息性删失时间,D为信息性删失时间.在研究复发事件数据时,可以假设在给定协变量的基础上,删失时间Y与个体所发生的事件次数是独立的.

设Z是取非负值的潜在脆弱变量,用来表示复发事件过程N(·)和删失事件(C,D)之间的关联.设X是改变风险的乘法效应的p维协变量,W是改变时间指数尺度效应的q维协变量,注意这两者可能相同.设N(·)、C、D是相互独立的.

以(Z,X,W)为条件,由λ(t)dt=E[dN(t)|Z,X,W]定义的计数过程N(·)的速率函数采用以下形式:

(1)

在模型(1)的条件下,定义N(·)的累积均值函数为Λ(t)=E[N(t)|Z,X,W],即

Λ(t)=ZΛ0(tWTβ+1)exp(XTα).

(2)

模型(2)显示了W和X的不同效应.

2 参数估计

2.1 参数β的估计

假设对i=1,…,n,观察数据Xi、Wi、Ni(t),Yi(0≤t≤Yi)是独立同分布的.设mi是个体i在时间Yi之前的事件数,如果mi>0,则Ni(t)的跳跃时间为观测事件时间tij,j=1,…,mi.对于p维向量b,考虑变换

t*(b)=tWTb+1,Y*(b)=YWTb+1.

变换后的复发事件的计数过程为

在模型(1)的基础上有

特别地,当b=β时有

(3)

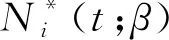
首先考虑的Λ0(t)一致估计量.对于任意固定的b,定义两个经验过程Qn(t;b)和Rn(t;b):

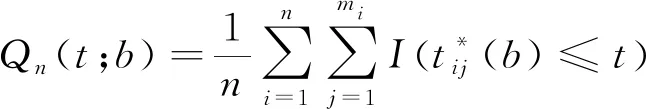
Qn(t;b)和Rn(t;b)的极限函数分别记为Q(t;b)和R(t;b).在模型(1)和(2)的条件下有

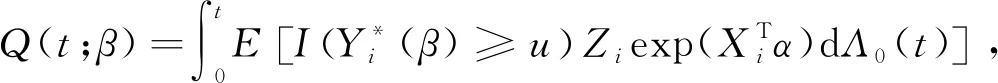
由Λ0(τ)=1得

(4)

由此得到Λ0(t)的一致估计量

(5)

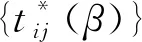
前面的讨论假设β是已知的.现在构造β的估计方程.定义[0,τ]上的随机过程

根据模型(3),对于t∈[0,τ]有

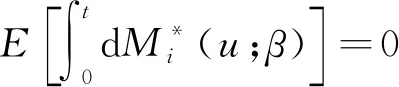
(6)

由(6)的第一式得到H的一致估计量

(7)

2.2 参数α的估计

在参数β的估计的基础上进一步对参数α进行估计.由(1)和(2)可得

当β和Λ0为已知条件时,有估计方程

(8)

3 估计量的渐近性质

为了研究所提出的估计量的大样本性质, 本文加了如下的正则性条件:

条件2协变量W和X是一致有界的,并且E(Z2)<∞.

条件3在(X,W,Z)的条件下,Y条件概率密度函数是连续且一致有界的.

条件4速率函数λ0(t)在区间[0,τ]上恒取非负值,且有有界的二阶导函数.

条件5定理中定义的J和J2是非奇异矩阵.

在上述条件下有以下渐近结果.

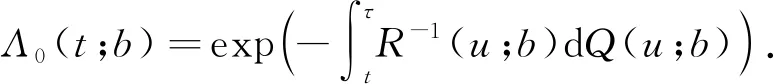
于是有

其中

由泰勒展开公式可得

(9)

我们有以下事实(证明参考[9,Theorem3.1]):

又由于

故由泰勒展开公式得

因此对于‖b-β‖≤dn→0,t∈[0,τ],有如下表示:

进一步有

因为

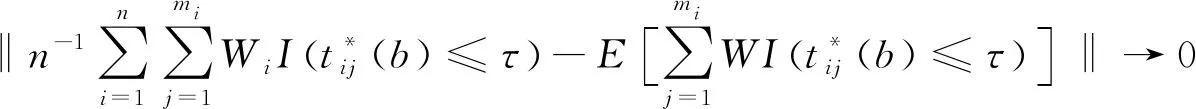
故由Glivenko定理([12,Theorem 2.4.3])得

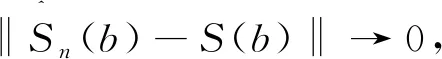
其中

又因为

故

故有

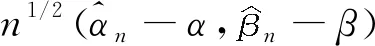
证明定义

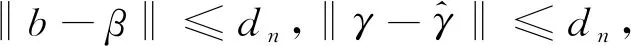
因此,下列结果对于考虑的结果是一致的:

其中

进一步推导Un(γ;β)的渐近正态性.Un(γ;β)可写为

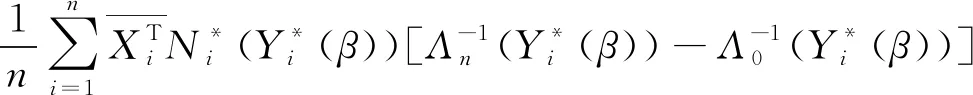
这里V(x,y,w,m)是(X,Y,W,m)的联合分布函数.因此

给出了n1/2Un(γ;β)的渐近正态性,其渐近均值为0,协方差矩阵为E[ci(γ;β)ci(γ;β)T].

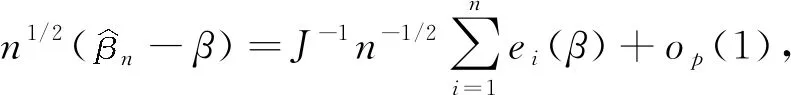
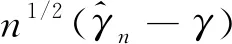
4 数值模拟

本节通过数值模拟研究前面提出的估计的样本性质,其中样本偏差(Bias)、样本均方误差(MSE)、平均标准误差(SE)和95%的经验覆盖概率(CP)用来评估估计结果.

4.1 数值模拟参数设置

在本次数值模拟中总共生成500个数据集, 每个数据集的样本量n分别设置为n=100和n=400.对于研究的个体i,设置协变量Xi=(Xi1,Xi2),其中Xi1为成功概率为0.5的二项分布,Xi2由均匀分布U=(0,1)独立生成.脆弱变量Zi设置为由均值为0.4,方差为0.08的伽马分布生成Z～Gamma(2,5).假设协变量Wi=Xi,复发事件过程观测截止时间τ=10,失效事件时间Di是当Xi1=1时由均值为10的指数分布生成的,当Xi1≠1时由均值为100/Zi的指数分布生成的,删失时间为Yi,Yi=min(Ci,Di).对于样本量n,回归参数α和β设为

(α,β)=((-3,3)T,(-0.5,0.5)T), (α,β)=((-3,3)T,(-0.3,0.1)T), (α,β)=((-3,3)T,(-0.2,0.4)T).情形1基准强度函数为λ0(t)=t/10.

情形2基准强度函数为λ0(t)=log(1+t).

4.2 数值模拟结果

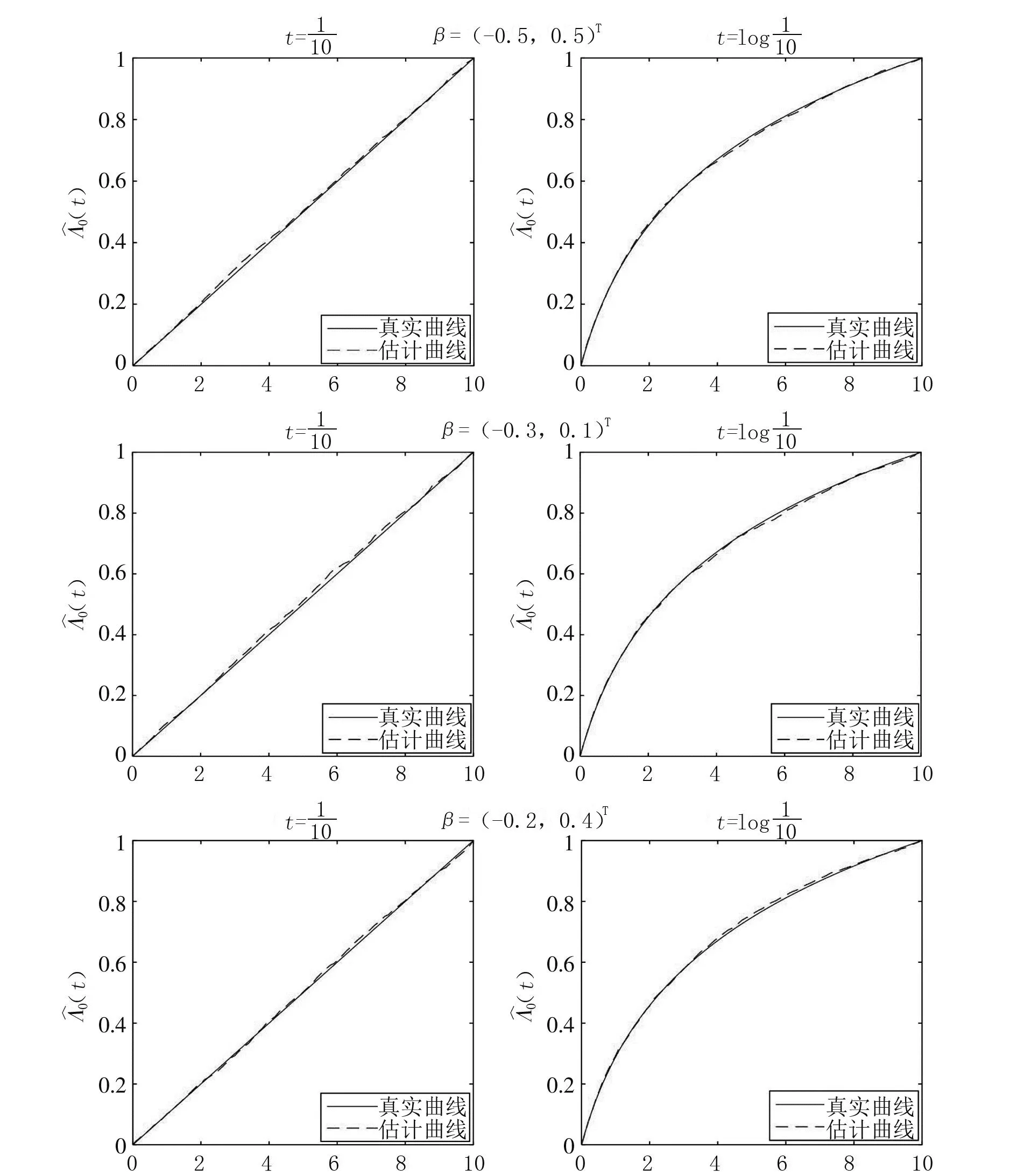
图1 n=100时的拟合曲线

图2 n=400时的拟合曲线

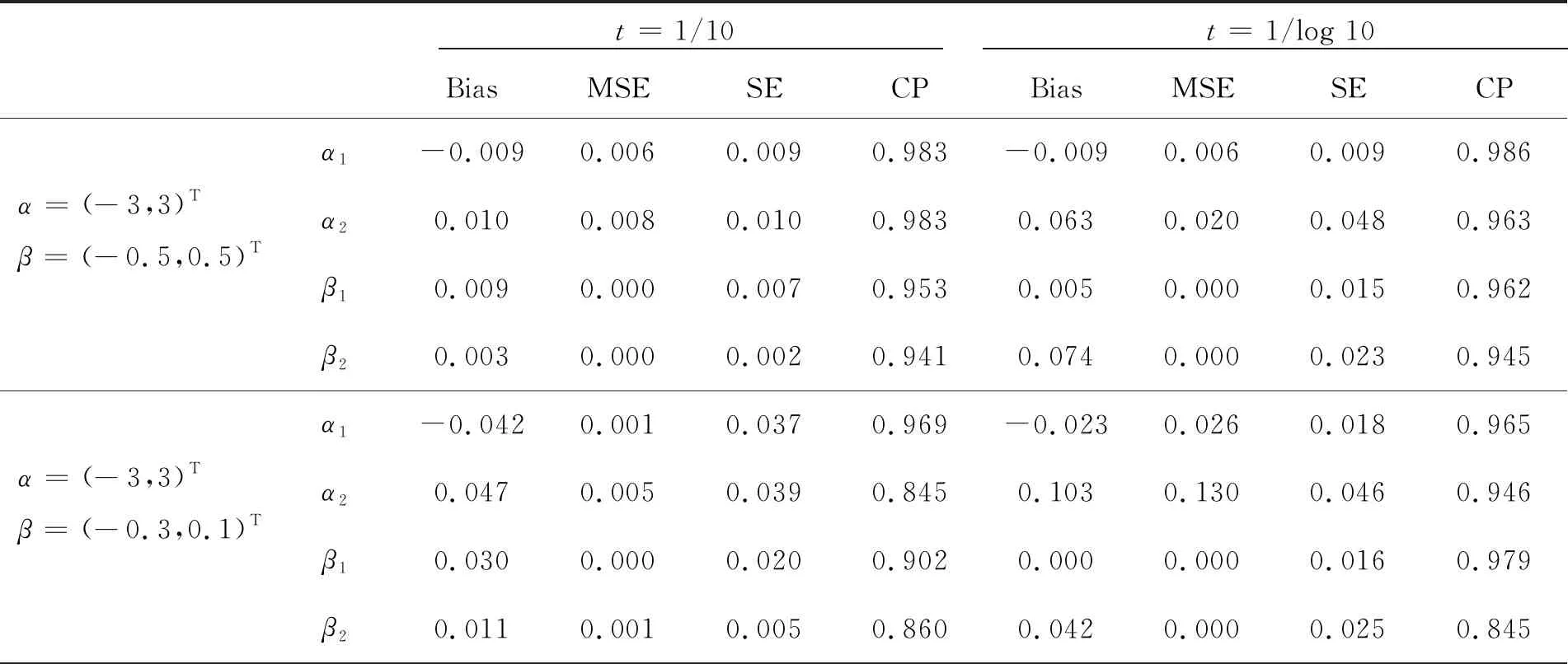
表2 n=400时的模拟效果

5 总结

本文拓宽了现有文献中模型的应用条件,提出了一种既不需要脆弱性分布的参数假设,也不需要重复事件过程的泊松假设的半参数估计模型.该模型协变效应分别为改变时间指数尺度效应和改变风险的乘法变化效应.本文对于模型的可识别性,假设Λ0(τ)=1,同时估计uz.使用广义估计方程的方法和随机过程理论对模型参数进行估计,证明估计参数的相合性和渐近正态性.利用MATLAB软件对估计参数进行数值模拟检验,验证了估计参数的渐近正态性.数值模拟结果表明,本文提出的估计方法表现良好,估计值与真值偏差较小,几乎无偏.