Frobenius函子和投射余可解Gorenstein平坦模*

刘义佳

(重庆师范大学 数学科学学院,重庆 401331)

本文中的环均指有单位元的结合环,模均指酉模.对于环R,用Rop表示R的反环,RM和MR分别表示左R-模范畴和右R-模范畴,I(R)和P(R)分别表示内射左R-模范畴和投射左R-模范畴.记号SMR表示M是(S,R)-双模.

Gorenstein同调代数可追溯到1969年Auslander和Bridger[1]对双边Noether环上的有限生成模的G维数的研究.20世纪90年代,Enochs等[2]对结合环引入了Gorenstein投射(内射、平坦)模的概念.2004年Holm[3]研究了Gorenstein同调模及其维数的性质.在Gorenstein同调代数的研究中,人们发现经典同调代数中一些关于投射(内射、平坦)模的同调性质和不变量的结论在Gorenstein同调代数中有对应的版本.众所周知投射模都是平坦模,但Gorenstein投射模是否都是Gorenstein平坦模仍是一个未解决的问题.为了研究这个问题,2020年Saroch和Stovivcek[4]引入了投射余可解Gorenstein平坦模的概念.

环的Frobenius扩张是一个经典的问题.1954年Kasch[5]引入了Frobenius扩张的概念,它是域上的Frobenius代数的推广.1960年Nakayam[6]等和Morita[7]发展了Frobenius扩张理论.1999年Kadison[8]引入了Frobenius双模的概念.Frobenius双模与模范畴之间的Frobenius函子具有一一对应关系[7,9],因此Frobenius函子可看作Frobenius双模的范畴版本[10].近来,Hu等[11]研究了Frobenius函子和Gorenstein平坦模及其维数之间的关系,Chen等[10]研究了Frobenius函子作用下的Gorenstein同调性质.

受以上研究的启发,本文研究投射余可解Gorenstein平坦模及其维数在Frobenius函子作用下的同调不变性.设R和S是环,SMR是Frobenius双模且MR是生成子.我们先证明了对任意R-模X,X是投射余可解Gorenstein平坦的当且仅当M⊗RX是投射余可解Gorenstein平坦S-模.然后证明了当F:RM→SM是忠实的Frobenius函子时有PGfd(RX)=PGfd(SF(X)).接着说明投射余可解Gorenstein平坦模及其维数在环的Frobenius扩张下是保持的.最后证明了若环的Frobenius扩张是可裂的,则环的PGF整体维数也具有不变性.

1 预备知识

定义1[8]如果(S,R)-双模M满足以下条件,则称M是Frobenius双模:

(1)SM和MR均是有限生成投射的.

(2) 存在(R,S)-双模的同构:

*M∶=RHomS(M,S)S≅RHomRop(M,R)S=∶M*.

定义2[6]称环扩张S→R是Frobenius扩张,如果下列等价条件之一成立:

(1)SR是有限生成投射的,且

RRS≅(SRR)*≅HomS(SR,SS).

(2)RS是有限生成投射的,且

SRR≅(RRS)*≅HomSop(RS,SS).

由以上定义可知环扩张S→R是Frobenius扩张当且仅当R作为(S,R)-双模是Frobenius双模.

定义3[9,12]设A和B均为Abel范畴,F:A→B,G:B→A是两个函子.

(1) 称(F,G)是伴随对,如果存在自然同构

HomB(F(-),-)≅HomA(-,G(-)).

此时称G是F的右伴随,F是G的左伴随.

(2) 称(F,G)是Frobenius对,如果G既是F的左伴随又是它的右伴随.

(3) 称函子F是Frobenius函子,如果对函子G,(F,G)是Frobenius对.

由定义可知若(F,G)是Frobenius对,则F和G均是Frobenius函子,即Frobenius函子总是成对出现的.根据[9,Theorem 2.1],函子F:RM→SM是Frobenius函子当且仅当存在Frobenius双模SMR使得F≅M⊗R-.

以下是一些常见的Frobenius函子.

例1[10](1) 设SMR是Frobenius双模,N是(R,S)-双模,则(M⊗R-,N⊗S-)是RM与SM之间的Frobenius对.

(2) 设S→R是环的扩张,则有纯量扩张函子R⊗S-:SM→RM和遗忘函子U:RM→SM,且环扩张S→R是Frobenius扩张当且仅当(R⊗S-,U)是Frobenius对.

本文将用到Frobenius双模的如下基本性质.

引理1[8,13]设R和S是环,SMR是Frobenius双模,记N∶=*M,则有:

(1)RNS是Frobenius双模.

(2)M⊗R-≅HomR(N,-),N⊗S-≅HomS(M,-).

(3) HomRop(M,-)≅-⊗RN, HomSop(N,-)≅-⊗SM.

(4) 若X是投射(内射,平坦)R-模,则M⊗RX是投射(内射,平坦)S-模.

(5) 若Y是投射(内射,平坦)S-模,则HomS(M,Y)是投射(内射,平坦)R-模.

(6) 对任意i≥0、任意Rop-模X和R-模Y,有

下面叙述投射余可解Gorenstein平坦模的概念及相关结论.

定义4[3,4]设X是R-模.

(1) 称X是Gorenstein投射的,如果存在投射R-模的正合列

P:…→P-2→P-1→P0→P1→P2→…,

使得X≅Ker(P0→P1),且对任意Q∈P(R),序列HomR(P,Q)仍正合.用GP(R)表示Gorenstein投射R-模类.

(2) 称X是Gorenstein平坦的,如果存在平坦R-模的正合列

F:…→F-2→F-1→F0→F1→F2→…,

使得X≅Ker(F0→F1),且对任意I∈I(Rop),序列I⊗RF仍正合.用GF(R)表示Gorenstein平坦R-模类.

(3) 称X是投射余可解Gorenstein平坦的(简称为PGF模),如果存在投射R-模的正合列

P:…→P-2→P-1→P0→P1→P2→…,

使得X≅Ker(P0→P1),且对任意E∈I(Rop),序列E⊗RP仍正合.用PGF(R)表示投射余可解Gorenstein平坦R-模类.

由以上定义可知PGF(R)⊆GF(R).由[4,Theorem4.4]知PGF(R)⊆GP(R).

引理2[4]PGF(R)关于扩张和直和项封闭.

引理3[14]对于R-模X,下列条件等价:

(1)X∈PGF(R).

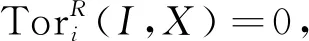
(3) 存在R-模的短正合序列0→X→P→G→0,使得P∈P(R),G∈PGF(R).

2 主要结果

本节先讨论在Frobenius函子作用下PGF模及其维数的同调不变性,作为应用给出PGF模及其维数在环的Frobenius扩张S→R下的同调不变性;然后讨论在Frobenius函子作用下Gorenstein平坦模、Gorenstein投射模和PGF模之间的关系;最后讨论环的PGF整体维数在可裂Frobenius扩张下的保持性.

引理4 设SMR是Frobenius双模,则有:

(1) 若X是PGFR-模,则M⊗RX是PGFS-模.

(2) 若Y是PGFS-模,则HomS(M,Y)是PGFR-模.

证明(1) 设X是PGFR-模,则存在投射R-模的正合列

P:…→P-2→P-1→P0→P1→P2→…,

使得X≅Ker(P0→P1),且对任意E∈I(Rop),序列E⊗RP仍正合.由引理1,有投射S-模的正合列

M⊗RP:…→M⊗RP-1→M⊗RP0→M⊗RP1→M⊗RP2→…,

且M⊗RX≅Ker(M⊗RP0→M⊗RP1).设I∈I(Sop),则I⊗SM是内射Rop-模,因此序列I⊗SM⊗RP正合.故M⊗RX是PGFS-模.

(2) 设Y是PGFS-模.因为RNS是Frobenius双模,因此由(1)可知N⊗SY是PGFR-模.由引理1知N⊗SY≅HomS(M,Y),故HomS(M,Y)是PGFR-模.

由[11,Theorem 2.2]知,函子F:RM→SM是忠实的Frobenius函子当且仅当存在Frobenius双模SMR使得F≅M⊗R-且MR是生成子.由此可得

定理1设SMR是Frobenius双模且MR是生成子,则有:

(1)X是PGFR-模当且仅当M⊗RX是PGFS-模.

(2)Y是PGFRop-模当且仅当HomRop(M,Y)是PGFSop-模.

证明(1) 必要性由引理4可得.下证充分性.设X是R-模,使得M⊗RX是PGFS-模.以下只需证明X是PGFR-模.

设E是内射Rop-模,则HomRop(M,E)是内射Sop-模.因M⊗RX是PGFS-模,故对任意i>0有

由同构

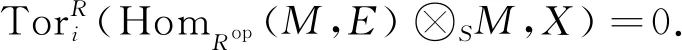
由引理4知HomS(M,M⊗RX)是PGFR-模,故存在短正合列

0→HomS(M,M⊗RX)→P0→L1→0,

使得P0是投射R-模,L1是PGFR-模.由[11,Theorem2.2]知,存在R-模的短正合列

考虑推出图

用函子M⊗R-作用后可得

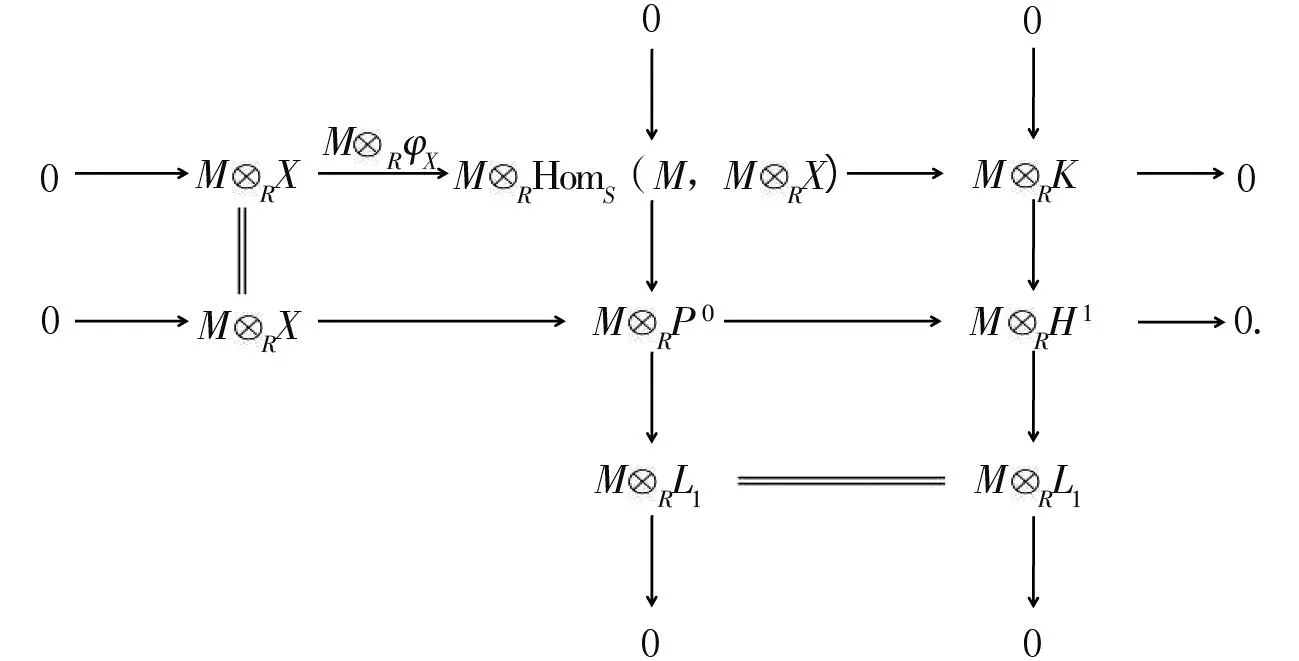
(2) 由于SMR是Frobenius双模且MR是生成子,故RNS是Frobenius双模且RN是生成子.由(1)知Rop-模Y是PGF模当且仅当Y⊗RN是PGFSop-模,故由同构Y⊗RN≅HomRop(M,Y)知HomRop(M,Y)是PGFSop-模.证毕.

若S→R是环的Frobenius扩张,则SRR是Frobenius双模且RR是生成子,因此R⊗R-:RM→SM是忠实的Frobenius函子.于是由定理1可得

推论1设S→R是环的Frobenius扩张,X是R-模,则X是PGFR-模当且仅当X是PGFS-模.

文献[15]证明了任意PGFR-模在环的可分Frobenius扩张下是保持的,因此上述推论是对[15,定理1]的推广.鉴于PGF模既是Gorenstein平坦模又是Gorenstein投射模,下面讨论在Frobenius函子作用下Gorenstein平坦模、Gorenstein投射模和PGF模之间的关系.由定理1和[11,Theorem 3.3,Theorem 3.4]可得如下推论.

推论2设SMR是Frobenius双模且MR和SM均是生成子,则有:

(1) 每个Gorenstein平坦R-模都是PGF模当且仅当每个Gorenstein平坦S-模都是PGF模.

(2) 每个Gorenstein投射R-模都是PGF模当且仅当每个Gorenstein投射S-模都是PGF模.

证明只证(1).必要性:设Y是Gorenstein平坦S-模,则由[11,Theorem 3.3(2)]知HomS(M,Y)是Gorenstein平坦R-模,从而是PGFR-模.因为SM是生成子,故由定理1(2)知Y是PGFS-模.

充分性:设X是Gorenstein平坦R-模,则由[11,Theorem 3.3(1)]知M⊗RX是Gorenstein平坦S-模,从而是PGFS-模.因为MR是生成子,故由定理1(1)知X是PGFR-模.

定义5[16]设X是任意R-模,X的投射余可解Gorenstein平坦维数(简称为PGF维数)为

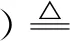
若不存在这样的n,则记PGfd(RX)=∞.环R的PGF整体维数为

引理5[15]设X是R-模,则下列两条件等价:

(1) PGfd(X)≤n.

(2) 若存在正合列

0→K→Pn-1→…→P1→P0→X→0,

其中Pi是PGFR-模,则K是PGFR-模.

下面利用上述引理讨论PGF维数在忠实的Frobenius函子作用下的不变性.

定理2设F:RM→SM是忠实的Frobenius函子,X是R-模,则PGfd(RX)=PGfd(SF(X)).证明因F是忠实的Frobenius函子,故存在Frobenius双模SMR且MR是生成子,使得F≅M⊗R-.设X是R-模,易知PGfd(SM⊗RX)≤PGfd(RX),所以只需证明PGfd(RX)≤PGfd(SM⊗RX).

PGfd(SM⊗RX)=∞时结论显然成立.设PGfd(SM⊗RX)=m<∞.考虑R-模的正合列

0→K→Gm-1→…→G1→G0→X→0,

其中Gi是PGFR-模(0≤i≤m-1).由定理1知M⊗RGi是PGFS-模,故有S-模的正合列

0→M⊗RK→M⊗RGm-1→…→M⊗RG1→M⊗RG0→M⊗RX→0,

其中M⊗RGi是PGFS-模(0≤i≤m-1).因PGfd(SM⊗RX)=m,故M⊗RK是PGFS-模,于是由定理1知K是PGFR-模,从而由引理5可得PGfd(RX)≤m.证毕.

由定理2可得如下推论.

推论3设S→R是环的Frobenius扩张,X是R-模,则PGfd(RX)=PGfd(SX).

文献[15]中证明了模的PGF维数在环的可分Frobenius扩张下是保持的,故推论3是该结论的一个推广.

推论4设SMR是Frobenius双模,则有:

(1) 若MR是生成子,则PGF-gl.dim(R)≤PGF-gl.dim(S).

(2) 若SM是生成子,则PGF-gl.dim(S)≤PGF-gl.dim(R).

证明只证(1).PGF-gl.dim(S)=∞时结论显然成立.设PGF-gl.dim(S)=m<∞,X是R-模.由定理2可得PGfd(RX)=PGfd(SM⊗RX),进而PGfd(RX)≤m.故PGF-gl.dim(R)≤PGF-gl.dim(S).

称环扩张S→R是可裂的[17],如果作为(S,S)-双模S是R的一个直和项.众所周知,如果环的Frobenius扩张S→R是可裂的,则SR是生成子.从而有以下推论.

推论5设S→R是环的可裂Frobenius扩张,则有:

(1) PGF-gl.dim(R)=PGF-gl.dim(S).

(2) 每个Gorenstein平坦R-模是PGF模当且仅当每个Gorenstein平坦S-模是PGF模.

(3) 每个Gorenstein投射R-模是PGF模当且仅当每个Gorenstein投射S-模是PGF模.