面向复杂曲面力控抛光的变阻抗控制研究*

刘钦超,崔 龙

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室,沈阳 110016;2.中国科学院机器人与智能制造创新研究院,沈阳 110169;3.中国科学院大学,北京 100049)

0 引言

随着现代工业化的发展,机器人开始在加工行业逐步取代人工。部分作业对机器人的接触力与位置协调控制性能有较高的要求,如抛光、磨削、装配等。在复杂曲面的力控抛光作业中,刀具的进给速度与接触力的波动或误差较大会影响抛光的质量,严重时甚至会对机器人本身造成损害。因此,研究如何同时精确对机器人末端刀具进给速度与刀具与环境之间接触力对提高抛光加工质量有着重要意义。对此许多学者进行了大量研究,并取得了很多的成果[1-2]。

力控抛光属于柔顺控制作业,其控制方法方法可大致分为直接法和间接法两大类[3]。直接法是RAIBERT等[4]提出的力位混合控制,其将任务空间分为力控子空间和位控子空间,直接控制力及位。间接法是HOGAN[5]提出的阻抗控制,通过阻抗模型构建力和位置的动态关系以实现柔顺控制。在非结构化环境下阻抗控制鲁棒性更强,其中导纳控制(基于位置的阻抗控制)在力控制领域应用较为广泛。有许多研究者将力位混合的思想与阻抗控制相结合使用,即混合阻抗控制[6]。

固定参数的阻抗控制难以实现复杂曲面接触力的稳定跟踪。研究表明,基于环境参数实时估计以修正阻抗系数可扩大控制器的稳定域[7]。SERAJI等[8]使用接触力误差动态更新阻尼系数的方式以降低环境参数误差对力跟踪的影响。ERICKSON等[9]使用接触力误差在线估计环境阻尼刚度模型以提高控制性能。许多研究者也使用神经网络、模糊系统、强化学习等方法来优化柔顺算法,但此类方法计算性能要求较高、系统的实时性差,目前难以在工业上应用。

混合阻抗算法通常使用选择矩阵确定控制模式,故在期望进给速度和接触力方向时变的曲面抛光任务中,只能先将期望速度及力投影到选择矩阵设定好的方向,再以相应的力位控制模式间接实现对时变力位的同时控制。此方法会使力位控制信号之间存在严重的耦合,在期望速度及力的方向对应算法设定好实际力位控制方向偏差较大时,则难以同时控制力位。

针对上述问题,本文提出了一种基于时变力位混合框架及自适应导纳控制的力位混合控制算法。通过被加工曲面实时修正力位混合框架,减小接触力控制与切削速度控制之间的耦合,保证进给速度与接触力单独精确控制。并使用接触力与力位框架修正速度实时调节阻抗模型的阻尼参数,减小抛光作业的恒力跟踪误差。

1 时变力位混合框架设计

如图1所示建立坐标系。不失一般性,将曲面切削加工问题简化为机器人末端工具在世界坐标系{ow}的xw-zw平面进行力位混合控制,工具坐标系{ot}随曲面实时改变,将力位混合框架搭建在{ot}中,在xt方向跟踪进给速度、zt方向跟踪接触力。α为{ot}沿yw方向旋转的角度。

图1 坐标系示意图

Tr(k+1)=Tr(k)dTr(k)

(1)

(2)

位控子空间只跟踪进给速度,只需将力控子空间的控制量与dTr相结合。记zt方向的力控制修正速度为vc,记Td为最终期望轨迹,dTc为力控制修正矩阵,令dTrc=dTrdTc,可得:

Td(k+1)=Td(k)dTr(k)dTc(k)=Td(k)dTrc(k)

(3)

(4)

式(3)和式(4)为时变力位混合框架的力位控制量结合方法,示意图如图2所示,图中符号Λ表示由角度与位置得到齐次变换矩阵的组合过程。

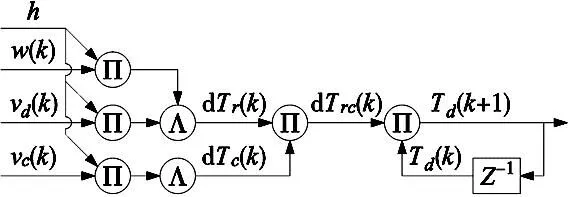
图2 时变力位混合框架的期望轨迹

2 自适应导纳控制算法设计

2.1 导纳控制模型推导及误差分析

推导时变力位混合框架的导纳控制器并分析接触力误差。时变力位混合框架只使用工具坐标系的姿态信息,为方便后续推导新增坐标系{oτ},坐标原点与{ow}重合,姿态与{ot}一致。

环境模型通常可采用一阶弹簧模型简化:

(5)

导纳控制的核心是通过阻抗模型计算力误差对应的位置修正量。用于力跟踪的阻抗模型通常使用刚度系数为0的二阶线性系统,所以力误差与位置修正速度vc的关系可用下式表示:

(6)

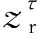
根据式(3)可求得关系:

(7)

(8)

将式(4)和式(7)代入式(8)可得:

(9)

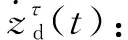
(10)

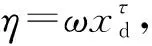
(11)

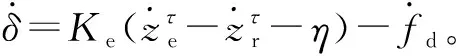
拉式变换可得δ到ef的传递函数:

(12)

式中:Ef(s)和Δ(s)为ef和δ的拉式变换。

(13)

2.2 自适应阻尼调节策略设计

令式(6)的b=b0+Δb,b0为阻尼初始设定值,Δb为阻尼修正值,整理可得:

(14)

文献[10]指出可通过添加ef的积分环节减小导纳控制的力跟踪误差,此外因为ω是扰动产生的根本原因,所以要加以补偿,故Δb采用下面的策略调整:

(15)

(16)

(17)

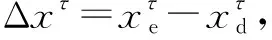
由式(16)可得:

φ(t)-φ(t-h)=ef(t-h)

(18)

拉式变换可得:

(19)

式中:Φ(s)是φ(t)的拉式变换。

所以新的传递函数为:

对上下左右四个方向产生的结果进行评估，评估方式为建立多个子算法加权得分，而得分最高的方向即为当前行动的最佳方向，下一步向该方向移动，为局部最优策略。由于不同子算法之间评判标准的不同，可能出现相互干扰，甚至相互对立的情况，同时不同时期受到的影响也可能不同，所以我们需要通过调整数字权重以及子算法权重完成优化，找到较好的评判标准，提高胜率。

(20)

因为控制周期h相较于系统其它参数非常小,所以可近似e-hs=1-hs,代入式(20)可得:

(21)

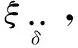
(22)

ef积分环节提高了系统的级数,降低了力控制器在接触力跟踪过程中的误差。并且可以通过合理设置ω补偿项的系数ρ减小式(22)的分子部分,也能减小误差。为直观展示本文控制算法的结构,给出算法框图,如图3所示。

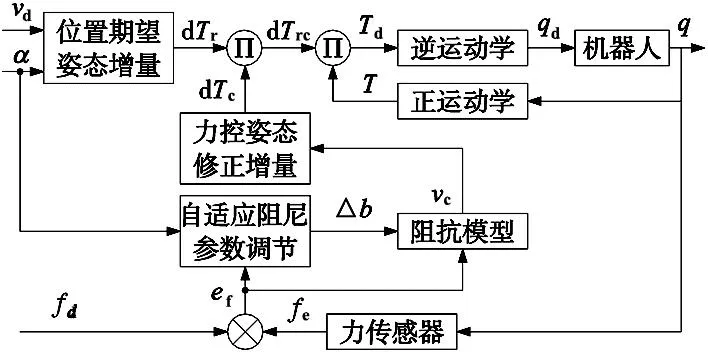
图3 算法框图

2.3 稳定性证明

由式(21)可得系统的特征方程为:

hms3+hb0s2+hKe(1-σ)s+σKe=0

(23)

可通过劳斯判据证明系统稳定性,如表1所示。

表1 控制器的劳斯表

令第1列的数据都大于0可得到系统稳定的条件:

(24)

3 算法验证

仿真硬件平台为配置了2.9 GHz的Intel(R) Core(TM) i7-10700F CPU的PC机,仿真软件为MATLAB R2020a的Simulink模块,仿真周期h设置为5 ms,环境刚度Ke设置为100 N/mm。

3.1 力位控制解耦仿真

期望进给速度为0.06 m/s,接触力为10 N。抛光曲面为内凹半圆型,如图4所示。控制器参数如表2所示,控制器1为基于选择矩阵的力位混合控制器,xw方向为位控子空间,zw为力控子空间,控制器2、3为本文基于时变力位混合框架的控制器。在半圆内部切削时的接触力误差、进给速度误差与曲面梯度信息α的仿真结果如图5所示。

表2 控制器参数

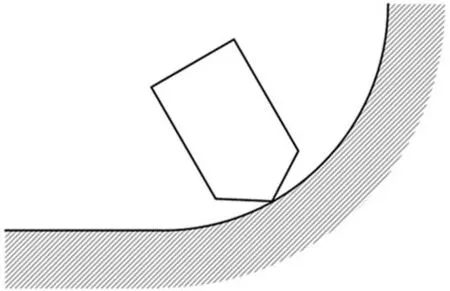
图4 半圆型曲面加工场景

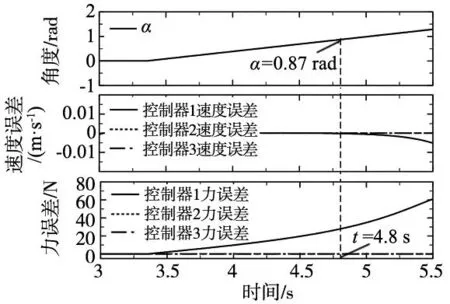
图5 半圆型曲面的控制器跟踪误差

从图5可以看出,在曲面的接触力跟踪中,基于选择矩阵的力位混合控制器难以对方向时变的期望接触力进行精确控制。并且在4.8 s之后,随着α的增加,当期望接触力方向与位置控制子空间夹角减小到一定角度(本场景为0.7 rad)后,进给速度的误差也逐渐增大,无法实现对速度精确控制。对于基于时变力位混合框架的控制器2、3,则可有效降低力位控制的之间的耦合作用,无论是否采用自适应阻尼调整策略都可实现期望力与切削速度的同时精确控制。

3.2 自适应阻尼调节策略仿真

由前文分析可知,接触力误差产生的原因主要是时变力位混合框架的修正速度ω。将图6中的控制器2、3的力误差曲线放大并与ω对比,可见对于固定参数的导纳控制器,当ω为恒定值时,力误差也近似为恒定值,且α的增大也会对力误差产生影响。使用自适应阻尼调节策略改进算法后则可保证力误差处于很小的值。

图6 半圆型曲面的控制器2、3接触力误差与力位框架修正速度关系

为进一步研究自适应阻尼调节策略下ef和ω的关系,继续在ω时变的曲面仿真,曲面方程按下式给定:

(25)

式中:θ为曲面调整参数。

θ取85°时的仿真数据如图7所示,结果验证了自适应阻尼调节策略能有效抑制ω对接触力误差的影响。为探究不同自适应参数对控制效果的影响,θ取89.99°以增大ω的变化速度及幅度,不同参数对力误差影响的仿真结果分别如图8所示。结果显示,在保证系统稳定下的条件下σ越大ef越小,而随着ρ的增加ef先减小后增大,所以需要合理设置参数ρ。将最佳参数所对应的最大力误差绝对值整理在表3,数据显示仅使用可降低误差93%,仅使用ρ可降低误差81%,同时使用则可降低误差97%,证明了本文的自适应阻尼调节策略的有效性。

表3 算法参数与最大力误差

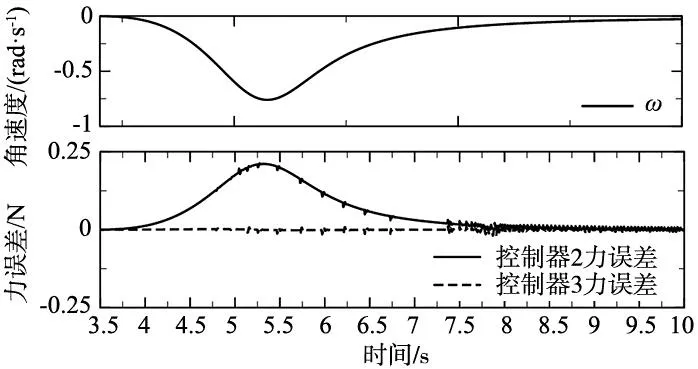
图7 控制器2、3的力误差与力位框架修正速度关系

图8 σ、ρ与接触力误差的关系

4 结论

本文主要研究了复杂曲面力控抛光作业中对同时控制方向时变的进给速度与接触力所面临的控制量相互耦合导致误差较大的问题,提出了一种基于时变力位混合框架及自适应导纳控制的力位混合控制算法。对仿真结果分析可得结论:

(1)时变力位混合框架相较于选择矩阵法可有效解耦进给速度与接触力,实现二者在复杂曲面抛光任务中的单独精确控制;

(2)使用接触力离散积分与力位框架修正速度的自适应阻尼调节策略可明显减小力控抛光作业的恒力跟踪误差。