基于WTMSE-AMCNN_1D的协作机器人故障诊断*

戴天赐,王 华,2,汪 健,董凌浩,李帅康

(1.南京工业大学机械与动力工程学院,南京 211816;2.江苏省工业装备数字制造及控制技术重点实验室,南京 211899)

0 引言

协作机器人是一种多模块集成的结构体,它作为一种新型工业机器人,长期以来被广泛应用于生产制造系统。但是在复杂的工况环境下,其出现故障的可能性也越来越大。协作机器人出现的不同故障会导致不同的影响结果,轻则影响生产效率,重则造成企业大规模经济损失。因此,对协作机器人进行有效故障诊断是尤为重要的[1]。

对于机器人故障诊断方法,主要分为模型驱动和数据驱动两大类。SABRY等[2]提出一种基于模型的故障诊断方法,建立Bode方程矢量拟合的模型来拟合机器人功耗,通过监视能耗率诊断故障轴。然而,该模型质量受诸多因素影响,因此,基于模型的机器人故障诊断精度较难提高。

近年来,数据驱动方法不断涌入故障诊断领域,其主要分为浅层学习和深度学习。浅层学习难以抽取故障信息,且准确率取决于提取的输入特征是否准确。在深度学习方面,主要包括CNN[3-5]、RNN[6]、自编码器[7]等。其中,由于CNN的端到端训练和其独有共享机制的优势,使得它在一维信号的故障诊断方面得到了广泛应用,李振东等[8]提出一种小波包能量谱和卷积神经网络结合的工业机器人故障诊断,然而该研究在将小波包能量谱转化为二维矩阵时增加了数据复杂度和矩阵稀疏性,不利于后续卷积处理。姜保军等[9]利用小波分解和样本熵构建特征向量,并最终准确诊断故障,可见小波分解和样本熵是一种有效的故障特征构建方法,且不会过于增加数据维度和矩阵稀疏性。

协作机器人是关节连接体,某关节的故障会影响其他关节的数据变化。因此,必须作整机为对象来研究。在机器人运行过程中,振动数据难以采集,而电流可以直接从控制箱拉取。针对协作机器人诊断问题,本文提出一种基于多尺度小波分解、样本熵(WTMSE)和一维注意力卷积神经网络(AMCNN_1D)相结合的协作机器人故障诊断方法,其可强化故障信息,增强模型泛化能力,提高模型效率。该方法首先是对原始电流数据采用随机采样的方法进行数据增强;接着将增强后的数据作小波分解,对分解系数进行样本熵计算,使结果作为引入注意力机制的一维卷积神经网络的输入并进行端到端训练;最后利用训练后的模型对协作机器人整机快速诊断分类。通过实验测试,并与其它模型对比,结果表明WTMSE-AMCNN_1D模型可以有效诊断协作机器人的故障。

1 协作机器人故障诊断模型构建

1.1 故障诊断模型结构

本文提出的基于WTMSE-AMCNN_1D故障诊断模型如图1所示。它包含两个部分,一部分是利用多尺度小波分解后的分解系数来进行多尺度样本熵计算的特征提取,另一部分是引入注意力层的一维卷积神经网络故障诊断分类。第一部分是特征提取,首先将原始六关节电流数据进行随机采样,然后对采样后的数据进行小波分解并根据分解系数计算其多尺度样本熵(MSE),将各个尺度的MSE合并成一个特征向量,最终得到多个MSE特征向量。第二部分是故障识别,即利用引入注意力层的一维卷积神经网络来诊断分类,它包含3个卷机块、1个注意力层和1个全连接层。后一部分将前一部分得到的MSE特征向量作为网络输入,最终输出是故障类别。

图1 WTMSE-AMCNN_1D模型

1.2 随机采样

通常情况下,由于获取故障样本比正常样本更困难,导致故障诊断数据集中不同类别的数据量不易平衡。因此,训练出来的模型对少量数据量的故障类型诊断效果较差。为了解决样本不平衡和训练过程中出现过拟合问题,本文采用随机采样[10]的方法,使各个故障类型的数据量在扩充的基础上又达到平衡,以此来提高模型的泛化能力。

随机采样是通过对原始时序序列随机选取采样点,并根据样本长度抽取所需样本量的过程。

1.3 多尺度小波分解和样本熵

在协作机器人运行过程中,由于所处工况环境问题,控制箱内部电路运行时可能会受到各种因素的影响,如电磁干扰、温度变化等,导致输出电路信号带有一定的噪声。对于原始的电流数据来说,它是一种非平稳且非线性的时间序列。为了解决该类时间序列数据中的信噪分离问题,小波分解方法得到了广泛应用。

多尺度小波分解是一种正交小波基构造方法,它可以将任意信号f(x)∈L2(R)分解为低频部分和高频部分,即近似部分和细节部分,其中近似部分能体现出信号的本质特征,而高频部分则能提现噪声相关信息。随着分解尺度的增加,其分解的系数长度会变得更短。所以f(x)可分解为:

f(x)=An+Dn+Dn-1+…+D2+D1

(1)

式中:An代表最后一层的近似部分,Dn到D1代表各分解层的细节部分,n是层数。对于任意Ψ∈L2(R),若小波函数Ψ(t)的傅里叶变换Ψ(w)满足式(2):

(2)

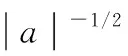
经过小波分解后,原始数据的故障特征也保留到了分解子频带中。为了提取到小波分解后的故障特征,本文计算了分解系数的多尺度样本熵(MSE)。这种方法是在样本熵的基础上改进的,具有较为强大的抗噪和抗干扰能力。下面是MSE的详细计算步骤:

步骤1:对于分解得到的分解系数X(i),(i∈[1,N]),利用以下粗粒化公式得到序列y(τ):

(3)

式中:τ是尺度因子,τ∈[1,N/τ]。

步骤2:对y(τ)计算不同尺度因子τ下的样本熵值,则多尺度样本熵为:

(4)

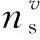
1.4 CNN神经网络

在深度学习里面,CNN神经网络是一种较为常见的网络,它是由卷积层,池化层和全连接层组成的。其中,卷积层的主要功能是通过卷积输入信号的局部感受域和卷积核来提取局部特征。每个卷积核都能够捕捉输入信号的一些局部特征,并在通过激活函数处理后构建输出特征向量。每一层的输出特征向量都是由多个输入特征通过卷积操作得到的。每一个卷积层的输出如下:

(5)

池化层的引入是为了减少输入特征的网络参数、在一定程度上防止过拟合。为了更好保留多尺度熵的主要特征,本文选取最大池化。

在卷积层和池化层组成的卷积块之后安排两个全连接层,第1个全连接层是把特征向量平铺成一维向量;第2个全连接层则采用Softmax分类器来进行最后的故障分类。

1.5 注意力机制

由于机器人在操作过程中会受到电磁干扰,在同种工况的不同时间内采集的协作机器人电流信号会有差异,从而导致提取出的特征不同。有些特征能表征故障信息,但有些会引入干扰,降低模型泛化能力。注意力机制[11]是通过自适应加权不同信号片段特征来筛选信息,突出有用的故障特征并抑制无效的特征。

近年来,注意力机制的结构得到很大改进,通过通道和空间注意力的结合实现了与卷积神经网络的联用,可在故障诊断和图像处理领域取得比单一CNN更好的效果。卷积注意力模块(CBAM)[12]结合通道注意力和空间注意力,可加入到不同的卷积层间实现特征权重的自适应调整。

1.6 协作机器人故障诊断流程

基于WTMSE-AMCNN_1D模型的协作机器人诊断流程分为3个部分,即数据预处理、模型训练、模型测试。诊断流程图如图2所示。

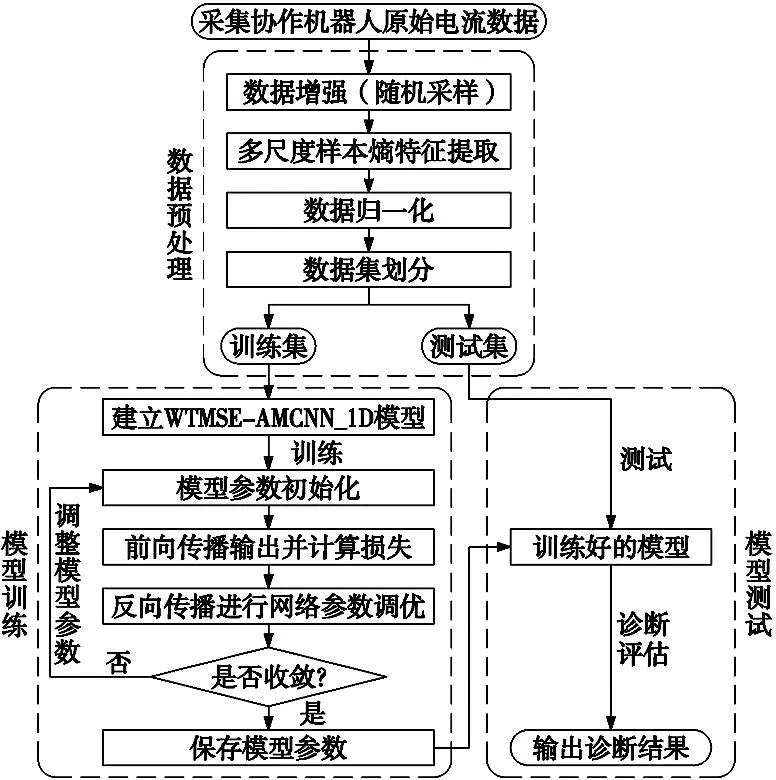
图2 协作机器人诊断流程

2 实验及故障数据集

在机器人运行过程中,关节螺栓可能会受到振动和冲击,长时间工作后会松动,最终导致机器人精度下降或者停机,而关节螺栓松动也可影响关节电流,所以本文使用某国产协作机器人运行时所采集的电流故障数据集作为数据来源,实验模拟关节螺栓松动为故障,实验采集频率为100 Hz,装置如图3所示。实验故障数据集包括4种工况下的电流数据,即正常运行数据、二关节故障数据、三关节故障数据和四关节故障数据。

图3 实验装置图

在采集过程中,设置在相同工况下运行,保证3种故障类型和一种正常类型的机器人运行动作一致。协作机器人电流故障数据集如表1所示。

表1 协作机器人故障数据集

由于关节较多,所以只展示二关节电流时序波形图,其如图4所示,可以看出即使在相同工况和同一运行动作下,二关节电流也有所差异,这说明采集电流信号可以有效诊断协作机器人故障。

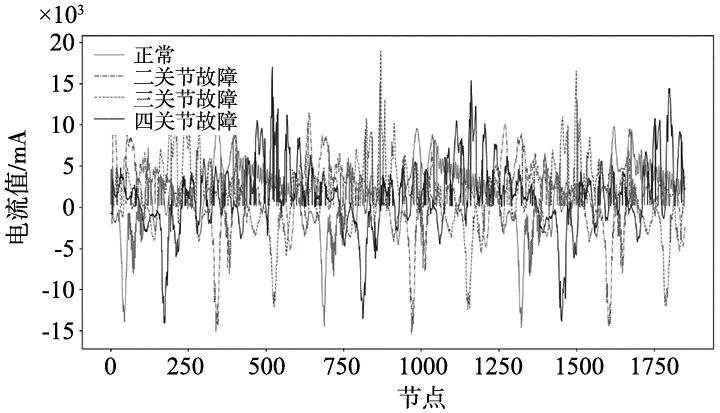
图4 二关节电流波形图

3 结果分析

本部分分为4个步骤:首先,为了验证随机采样方法对诊断准确率的影响,将采集的原始电流数据和经过随机采样处理的电流数据分别进行简单一维卷积(CNN_1D)诊断;然后对随机采样后的数据利用多尺度小波分解和样本熵的方法提取特征,分析不同小波分解层数对WTMSE-CNN_1D模型诊断准确率的影响程度;接着对比本文所提的WTMSE-AMCNN_1D模型与CNN_1D模型、WTMSE-CNN_1D模型诊断结果;最后为验证本文所提模型对协作机器人诊断的优越性,对比浅层学习的BP神经网络、随机森林以及较新的Transformer模型。

3.1 随机采样对比分析

随机采样可以解决样本不平衡和训练过程中出现过拟合问题。若将每类20万采样点作为数据,当样本长度为1000时,每类仅可生成200个样本,故在没有进行随机采样的方法下,每类样本量较少。而当原始数据进行随机采样后,可生成每类2000样本,总共8000个样本。为了验证随机采样方法对诊断准确率的影响,本文将采集的原始电流数据和经过随机采样处理的电流数据分别进行简单一维卷积诊断,诊断平均准确率如表2所示。

表2 CNN_1D下的平均诊断准确率

从表2可知,在得到采集的原始电流数后,将其直接作为简单一维卷积神经网络的输入,得到的诊断准确率为88.32%,在经过随机采样处理后,诊断精度提升了5%左右,这表明在样本较多的情况下,故障特征可以被模型更好的学习到。

3.2 小波分解层数对WTMSE-CNN_1D模型诊断准确率影响

由于采集的关节电流只有6个,特征数较少,进行卷积时可能会失去部分数据信息,影响模型的诊断性能。为此,采用第1.3节中的多尺度小波分解和样本熵的方法,在降噪的基础上提取更丰富的特征,有效学习数据中的信息。通常来说,小波分解层数不宜过多也不宜过少,因为层数越高,分解出的信息包含噪声信号可能就越多,从而影响诊断结果;分解层数越低时,可能会导致不能全面地反映原始信号特征。所以为探究小波不同分解层数对诊断准确率的影响,本文分别对6个关节电流进行2、3、4、5、6层小波分解来比较最终诊断准确率,结果如图5所示。

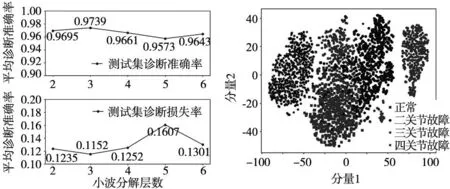
图5 WTMSE-CNN_1D下不同分解层数的诊断结果 图6 样本熵值可视化

由图5可知在3层小波分解后,特征模型诊断准确率最高,为97.39%。因此,在实际应用中,要根据信号和数据情况合理选择分解层数。

为了进一步说明选择小波分解来提取特征的可行性,取诊断准确率最高时小波3层分解后计算出的样本熵值,利用T-SNE[13]方法对计算出的样本熵值进行二维可视化,结果如图6所示。

从图中可以看出,对于小波分解后计算出的多尺度样本熵值,同一种类别的的值大致可以被聚集在一起,而不同类别的值被较好的分离开来。这说明原始电流信号经过多尺度小波分解和样本熵提取后所得到的特征可以有良好的分类效果。

3.3 WTMSE-AMCNN_1D与CNN_1D、WTMSE-CNN_1D诊断结果比较

由于注意力机制可以突出有用的故障特征并抑制无效的特征,故在WTMSE-CNN_1D模型中第3个卷积块后加入注意力层。在此层中,先通过一个全连接层计算出能量值,然后对其作归一化处理,得到注意力权重,接着将第3个卷积块的输出作为输入张量,并与注意力权重作加权处理,最终将得到加权后的输出传递给后面全连接层。本部分的故障数据集选取第3.1节中经过随机采样后的电流数据,即样本长度为1000,每类2000个样本,一共8000个样本,训练集和测试集按7∶3分配。对于WTMSE-AMCNN_1D模型,选取第3.2节中诊断准确率最高的三层小波分解来计算的多尺度样本熵值作为引入注意力层的一维卷积输入,其分析结果如下。

图7是利用T-SNE方法对全连接层输出值进行的二维可视化图,可以看出经过引入注意力层的一维卷积处理后,不同类别的输出值呈现出更好的分离状态,这远好于初始卷积输入的样本分类效果。

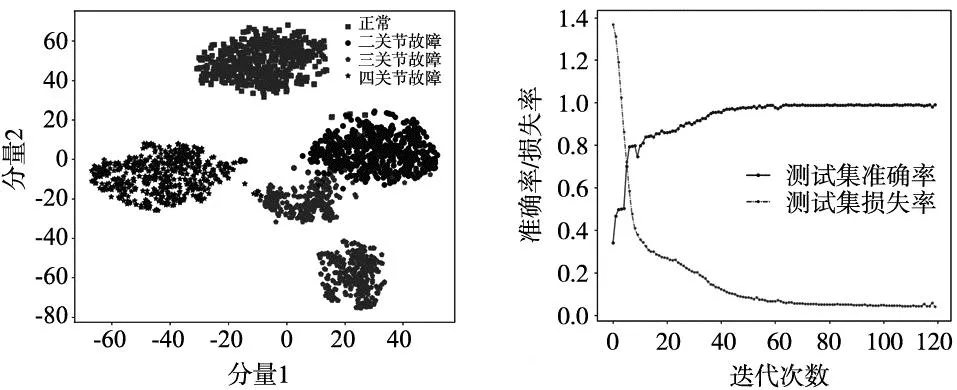
图7 全连接层输出值可视化 图8 WTMSE-AMCNN_1D训练过程

图8为本文所提诊断模型(WTMSE-AMCNN_1D)训练过程,测试集的诊断准确率可达到99.21%,损失率逐步下降并且趋于稳定。

根据第3.1和3.2节可知,没有经过多尺度样本熵特征提取的准确率为93.47%,经过特征提取的模型(WTMSE-CNN_1D)诊断准确率最高为97.39%,而引入注意力机制的模型(WTMSE-AMCNN_1D) 诊断准确率最高,为99.21%。由此可知在一维卷积中引入注意力层可以更好的区分有用信息和噪声,使得模型的诊断准确率提高。

为了进一步反映本文模型的故障识别能力,引入多分类的混淆矩阵来对故障详细分析,混淆矩阵如图9所示。

图9 混淆矩阵

由图9可知,根据8000个样本按照7∶3划分训练集和测试集,可以划分出测试集2400个样本,每种类别600个样本。其中仅有19个样本被误判,其余样本都被正确分类。由此可以看出WTMSE-AMCNN_1D模型的诊断精度最高,对于协作机器人具有更好的诊断效果。

3.4 其它模型诊断分析对比

为了进一步说明本文所提出的模型(WTMSE-AMCNN_1D)的优越性,将浅层学习的BP神经网络、随机森林模型以及较新的Transformer模型与之比较。诊断结果如表3所示,从中可以看出基于BP神经网络和随机森林的平均诊断准确率均远小于本文模型的平均诊断准确率,而专注分类任务的Transformer模型平均诊断准确率为96.57%,其也小于本文模型的平均诊断准确率。因此,本文所提的WTMSE-AMCNN_1D模型能够有效提高故障诊断准确率,且对协作机器人关节螺栓松动的故障分类任务具有较好的适用性。

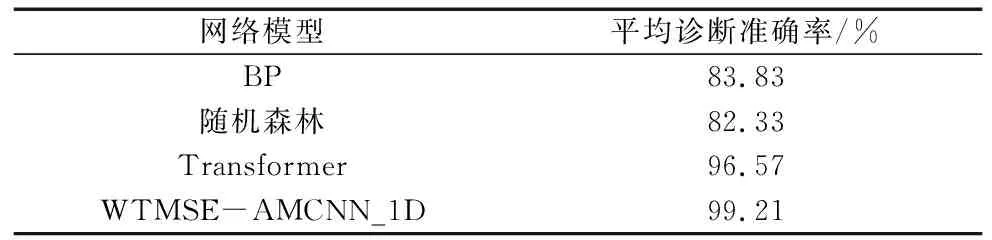
表3 浅层学习模型与WTMSE-AMCNN_1D的平均诊断准确率

4 结论

针对协作机器人故障诊断精度低且振动数据难以采集的问题,本文提出了一种基于WTMSE-AMCNN_1D的协作机器人电流信号故障诊断方法,首先对采集的电流信号数据进行随机采样,对比随机采样后的数据和原始数据的诊断效果,结果验证了随机采样的可行性;然后对比不同小波分解层数下WTMSE-CNN_1D模型的诊断精度,发现经过三层小波分解,诊断准确率最高,同时也说明了其计算出的多尺度样本熵值分类效果更好;接着对比本文所提模型与CNN_1D、WTMSE-CNN_1D的诊断结果,说明注意力机制可以充分挖掘出故障信息;最后为进一步说明本文模型的优越性,对比BP神经网络、随机森林和较新的Transformer模型,结果显示WTMSE-AMCNN_1D模型诊断准确率最高,可达99.21%,这表明本文所提模型可以有效诊断协作机器人故障,且对其关节螺栓松动的故障分类任务具有较好的适用性。