新型滑模观测器下的表贴式永磁同步电机控制*

纪明阳,孙志锋,,马风力,,黄 颖

(1.浙江大学电气工程学院,杭州 310027;2.杭州力超智能科技有限公司,杭州 311200)

0 引言

永磁同步电机(PMSM)以其自身结构简单、噪声小、可靠性强、高功率因数等优点,在实业领域应用广泛,如新能源汽车、医疗器械等[1]。在PMSM的实际使用中,需要准确地获取转子转速以及转子位置,从而实现对电机的精确控制。传统方法通过传感器实现电机转子信息的获取,但是也会产生电机控制系统整体成本增加、系统体积变大、传感器在外部环境中可能会受到干扰等问题,因此目前无传感器控制技术更加引人关注[2-3]。

PMSM的无传感器控制技术可分为基于高频信号数学模型的无传感器控制技术与基于基波数学模型的无传感器控制技术[4]。前者主要用于电机零速或低速运行时的场合;后者主要用于电机的中高速运行时的场合,通过定子的给定电流与反馈电流之间的差值重构反电动势,对反电动势的基波进行分析,估算出对应时刻转子速度与转子位置[5]。目前在基于基波数学模型的无传感器控制技术中,常用方法为滑模观测器算法[6]、模型参考自适应控制算法[7-8]、扩展卡尔曼滤波器算法[9-11]、神经网络算法[12]等。在诸多算法中,ZHANG等[13]进行了对比,其中龙贝格观测器实用性更好,但是滑模观测器整体系统的稳定性更好,而且由于其算法简单、对模型参数变化以及外部扰动不敏感,在实际应用中最为广泛,得到了许多学者的重视。

鲁文其等[14]提出将滑模观测器中的符号函数替换为饱和函数从而降低系统的抖振。随后许多学者提出了滑模观测器中切换函数的优化方案,彭思齐等[15]设计了边界层可变的分段二次函数,SONG等[16]设计了边界层可变的分段三次函数,袁潇等[17]提出将切换函数更换为光滑的Sigmoid函数。GONG等[18]提出了一种延时抑制的滑模观测器,利用双采样策略的电流补偿方案,提高电机转子位置估计的精度。张祺琛等[19]提出将传统滑模观测器中的等速趋近律替换为双幂次趋近律,并引入边界层可变的分段幂函数作为切换函数,降低系统的高频抖振。

本文提出了一种基于新型的滑模观测器下的电机控制系统。利用幂次趋近律与指数趋近律形成一般趋近律,采用积分滑模面替代传统滑模面,采用Sigmoid函数替代符号函数,采用模糊控制系统对切换函数的边界层相关系数进行自适应控制。尽可能削弱系统的抖振,同时提高对电机的转子速度以及转子位置的观测精度。通过Lyapunov第二方法验证系统稳定性。通过MATLAB/Simulink搭建系统模型进行仿真,并且与传统滑模观测器进行对比,证明了新型滑模观测器的更加良好的特性。

1 传统滑模观测器

目前大多数的传统滑模观测器均基于静止坐标系下的电机数学模型进行设计,针对表贴式PMSM的传统的SMO的设计为:

构建电机的电流状态方程:

(1)

式中:Ls为定子电感,uα与uβ为定子电压,iα与iβ为定子电流,R为定子电阻,Eα与Eβ为扩展反电动势。

为了获取扩展反电动势的估计值,从而作为传统SMO的控制输入,传统SMO的设计为:

(2)

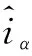
传统滑模观测器采用传统滑模面:

(3)

当SMO的状态变量达到sα=sβ=0之后,SMO的状态将一直保持在滑模面上。采用符号函数作为切换函数,根据滑模控制理论,此时的SMO控制输入可以看作为等效的控制量,即:

(4)

对式(5)中a的要求为:

a>max{-R|sα|+Eαsgn(sα),-R|sβ|+Eβsgn(sβ)}

(5)

在对于转子位置的估计中,由于传统SMO的控制量中符号函数的存在,因此扩展反电动势是一个不连续的高频切换信号,需要加入一个低通滤波器从而获取连续的扩展反电动势,方便后续计算。

(6)

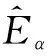
传统SMO中,对于转子位置信息的获取采用如下公式:

(7)

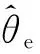
通过电机转子的位置信息,可以通过求微分运算获取转速信息。特殊情况下,对于表贴式的三相PMSM,可以通过下式对电机转速进行估算:

(8)

式中:φf为电机磁链。

综上所述,传统SMO的实现原理如图1所示。

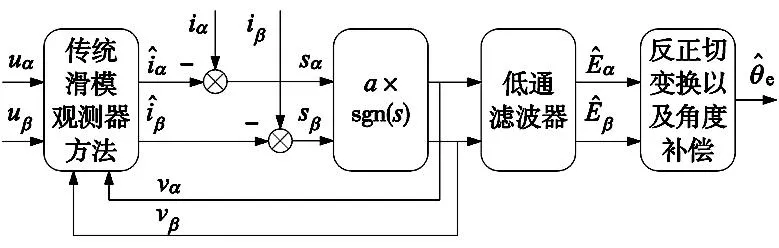
图1 传统滑模观测器的实现原理框图

2 针对表贴型永磁同步电机的新型滑模观测器的设计

2.1 滑模面的设计

在滑模面设计上,由于传统的SMO的滑模面基本采用定子电流的观测值与实际值之差作为滑模面,根据公式可见无法消除定子电阻带来的影响。为此采用王方凯文等[20]提出的积分滑模面代替传统滑模面,可以针对表贴式PMSM定义积分滑模面为:

(9)

式(9)与传统滑模面相比,积分滑模面由于含有了电机定子电阻作为参数,在后续的计算过程中会将定子电阻这一因素抵消,从而提高了滑模观测器的适用性。

2.2 切换函数设计

在切换函数设计上,传统的SMO采用了滑模变结构控制中的等速趋近律,即:

(10)

式中:a表示系统的运动点趋近切换面s=0的速率,a的值较小时,趋近速度较慢,导致系统响应速度慢;当a的值较大时,则运动点到达切换面会有较大的速度,引起的抖动也较大。

对切换函数的设计分为两部分。①将等速趋近律更改为指数趋近律与幂次趋近律结合的一般趋近律,即:

(11)

式中:第一项称为幂次趋近项,第二项称为指数趋近项。指数趋近项能保证当s较大时,系统状态能够以较大的速度趋近于稳定滑动模态;而当s较小时,指数趋近项会导致运动点到达切换面时的速度很小,并不能保证在有限时间内到达,此时幂次趋近项就能够保证在s接近于0时趋近速度不为0,保证在有限时间内到达切换面。而对于幂次趋近项来说,调整ε的值,可以保证当s较大时,运动点能够以较大的速度趋近滑动模态,s较小时保证较小的控制增益,降低抖振。因此该一般趋近律通过调整ε与k的值,从而保证系统稳定在滑动模态附近。

②将趋近律中的符号函数进行替换。传统SMO中在等速趋近律里采用符号函数,不仅会导致电机运行过程中产生较大的抖振,同时也需要增加低通滤波器以及相位补偿等冗余环节,因此需要将符号函数替换为效果更好的函数。一般而言,该函数需要有着这样的一些性质:函数有上下界,函数是连续的,函数最好是可导的。从而使切换函数尽可能是一个光滑的有界函数,避免电机运行过程中产生较大的抖振。

采用Sigmoid函数作为切换函数,从而减轻系统的抖振,表达式为:

(12)

此时滑模观测器的数学模型为:

(13)

定子的电流误差方程为:

(14)

2.3 切换函数特性分析

对于滑模观测器而言,切换函数是其中非常重要的一部分,不同的切换函数所带来的不同的曲线特性会导致滑模观测器的效果也不尽相同。传统SMO中使用的切换函数包括:符号函数、饱和函数、指数型切换函数等。将上述函数与Sigmoid函数作为对比,对比图如图2所示。图中的±σ定义为切换函数的边界层。

图2 滑模观测器中应用的不同切换函数

针对不同的切换函数进行分析:符号函数本身是不连贯的函数,因此控制量会在滑模面的附近产生突变,导致电机在运行过程中会存在较为严重的抖振现象,而且观测量与实际量之间的误差也会较大。

饱和函数作为连续函数,与符号函数相比,控制量不会产生突变,能够明显的削弱抖振,但是由于其本身不是平滑曲线函数,所以在边界层附近的抖振情况依旧存在。与符号函数相比,饱和函数应用在SMO中,观测量与实际量之间的误差会变小,但是其在边界层内不同误差下的增益变化单一的特点,只能确保一定程度上的观测精度的提高。

指数型切换函数在边界层内的平滑连续性很好,可以较好地削弱抖振现象。但是在边界层附近由于函数不平滑,因此当电流误差较大时会产生一定程度的抖振现象。此外,由于指数型切换函数自身在零点附近导数为0,因此当电流误差为0时,此时扩展反电动势为0,扩展反电动势的变化率也为0,导致根据SMO观测得到的扩展反电动势会产生一定程度的零点钳位现象,这会导致电机的转子位置计算出现偏差。

Sigmoid函数与上述函数相比有着自身的优点:无论是边界层内还是边界层附近,函数自身的平滑连续性会明显削弱抖振。Sigmoid函数也避免了零点附近导数为0或者导数无穷大的现象,既能避免扩展反电动势的钳位,又能避免系统的抖振。

3 新的滑模观测器的稳定性分析

对于滑模观测器系统而言,需要事先验证其稳定性,一般均采用Lyapunov稳定性判据对SMO进行稳定性分析,从而验证使用SMO观测PMSM的反电动势是否可靠。定义Lyapunov函数为:

(15)

(16)

对式(16)进行后续的详细计算可知:

(17)

4 模糊控制器设计

根据滑模控制理论,在滑模观测器中,切换函数的边界层厚度越大,系统的抖振程度越小,但是运动点到滑动模态的趋近速度会变慢,导致整体系统的响应速度变慢;而边界层厚度越小,运动点到滑动模态的趋近速度会加快,但是系统的抖振幅度会增加。因此需要在SMO的设计中对相关参数进行自适应调节,尽可能地削弱系统抖振的同时提高整体系统的响应速度。

可以采用模糊控制对参数进行调节,模糊控制是一种建立在人工经验基础上的控制系统,与传统控制方法相比较不需要了解被控对象的数学模型,其主要方法是将输入变量进行模糊化,通过设定的知识库与模糊逻辑,给出模糊化的输出集合,最后将输出集合进行反模糊化得到一个最佳的估计值作为输出变量。本文对于滑模观测器设计了新的切换函数:

(18)

式中:

1>ε>0,a>0,k>0

针对新的切换函数,有3个参数需要调节,ε、a与k。主要的调节思路为:将定子电流的观测值与实际值的差即s作为模糊控制系统的输入变量,ε、a与k作为模糊控制系统的输出变量。其中当s较大时,表明电流的误差较大,此时需要适当增大ε、a与k的值,令边界层厚度减小,同时加快运动点到滑动模态的趋近速度;当s较小时,表明此时运动点在滑动模态附近运动,此时需要适当减小ε、a与k的值,增加边界层的厚度,同时尽可能削弱系统的抖振现象。

对于模糊控制系统而言,首先需要定义输入输出变量并定义各个变量的模糊化条件。对于本文中设计的新型滑模观测器而言,输入变量为s,输出变量则为ε、a与k。输入变量的论域定义为{-1,1},输出变量ε的论域定义为{0,1},输出变量a的论域定义为{0,30},输出变量k的论域定义为{10,20}。输入变量s的模糊语言定义为为{NB,NM,NS,Z,PS,PM,PB},输出变量ε的模糊语言定义为{Z,PS,PM,PB},输出变量a的模糊语言定义为{Z,PS,PM,PB},输出变量k的模糊语言定义为{Z,PS,PM,PB}。各个输入以及输出变量所对应的隶属度函数采用常用的三角形函数,各个输入输出变量的隶属度函数如图3～图6所示。

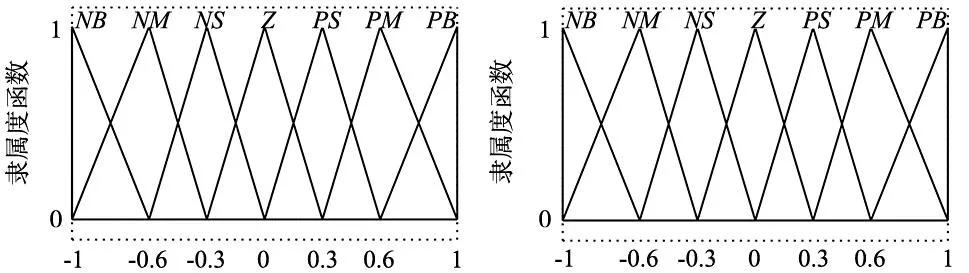
图3 输入变量s隶属度函数 图4 输出变量ε隶属度函数

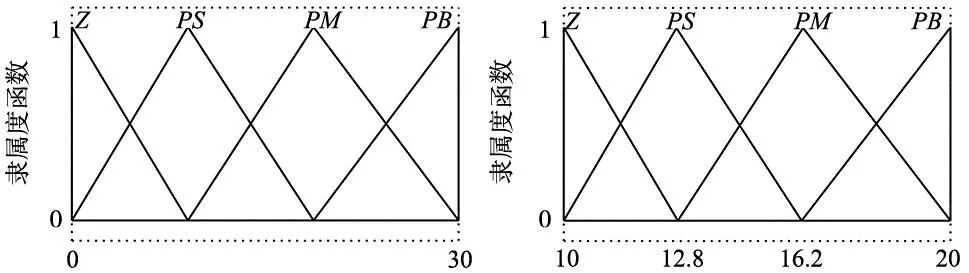
图5 输出变量a隶属度函数 图6 输出变量k隶属度函数

根据上述条件,以及预期的参数调节目标,设计模糊控制规则如下:

Rule 1:ifsisZthenεisPB,aisZandkisZ.

Rule 2:ifsisNSorPSthenεisPM,aisPSandkisPS.

Rule 3:ifsisNMorPMthenεisPS,aisPMandkisPM.

Rule 4:ifsisNBorPBthenεisZ,aisPBandkisPB.

在模糊控制系统中,采用Mamdani推理算法进行模糊推理,反模糊化过程中采用重心法,该方法具有更加平滑的输出推理控制效果。根据各个输入输出变量的隶属度函数以及模糊控制规则可以看出,当输入变量s的值发生变化时,输出变量的值符合预期设计。

将设计好的滑模面、切换函数与模糊控制系统相结合,形成新型的滑模观测器,其原理框图如图7所示。

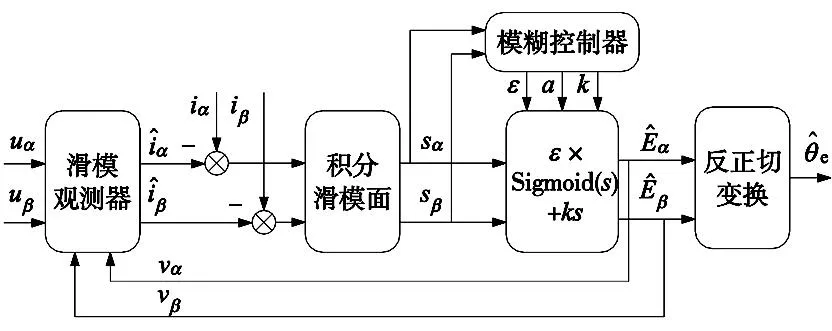
图7 新型滑模观测器的实现原理框图

5 仿真结果以及分析

采用MATLAB/Simulink平台搭建模型进行仿真从而对本文提出的新的滑模观测器的性能进行验证。在MATLAB/Simulink平台中搭建表贴式三相PMSM的无位置传感器控制系统。对于电机的矢量控制采用id=0控制,整体控制系统主要包括:SVPWM算法控制、电流环PI调节、转速环PI调节,滑模观测器用于提供电机的转子位置估计信息与转子速度估计信息。表贴式三相PMSM的无位置传感器控制系统的结构框图如图8所示。

图8 应用新型滑模观测器下的PMSM控制系统框图

仿真实验中表贴式PMSM的参数设计如表1所示。

表1 仿真实验中的表贴式PMSM参数

为了验证新型滑模观测器的优点,仿真实验采用对照实验的方式进行。电机的启动采用空载启动,参考转速设定为1000 rpm,在0.05 s时将参考转速提高至1500 rpm,在0.1 s时对电机施加10 N·m的转矩。下面各个波形为新型滑模观测器与传统滑模观测器在同一条件下得到的仿真波形。图9～图15分别为两种滑模观测器下的电机转速变化曲线、电机转速误差变化曲线、电机转子位置变化曲线、电机转子位置误差变化曲线、电机转矩变化曲线、电机三相电流变化曲线以及电机反电动势变化曲线。

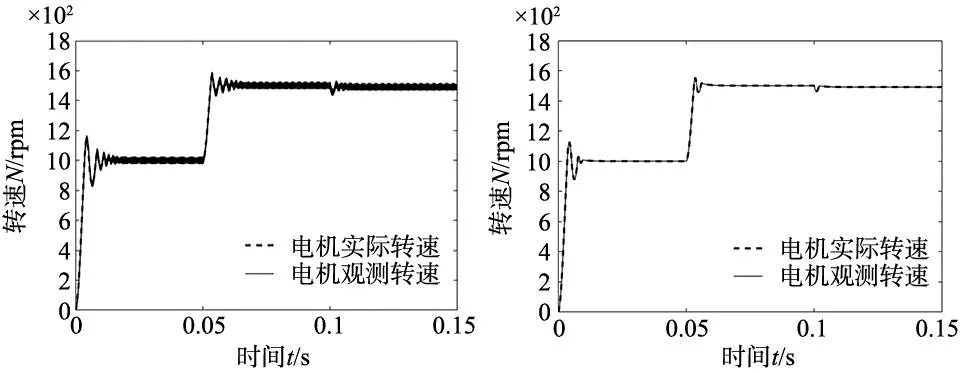
(a) 传统SMO电机转速 (b) 新型SMO电机转速图9 电机转速变化曲线

根据图9可知,无论是在电机转速出现突变还是在电机负载出现突变时,与传统滑模观测器相比,新型滑模观测器下电机能够更快地稳定电机转速,同时有着更小的转速波动。

根据图10可知,在电机转速稳定时,传统滑模观测器下电机转速的误差在-30～20 rpm之间,新型滑模观测器下的电机转速误差在±0.02 rpm以内。这意味着在电机稳定运行时,新型滑模观测器能够更好地对电机转速进行检测。

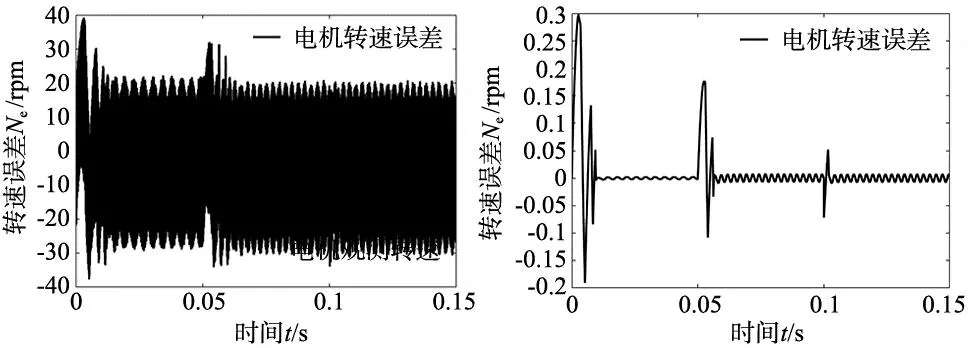
(a) 传统SMO电机转速误差 (b) 新型SMO电机转速误差图10 电机转速误差变化曲线

根据图11与图12可知,在电机稳定运行过程中,传统滑模观测器下电机转子位置的误差在变化范围在±π/2之间。新型滑模观测器下的误差在0-π/2之间。在电机启动阶段,传统滑模观测器下转子位置的观测值与实际值有着较大的误差,新型滑模观测器下则能够较好地追踪转子位置的变化。

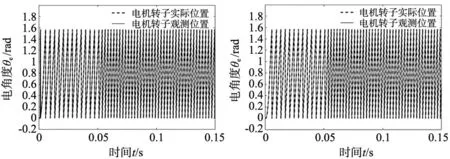
(a) 传统SMO电机转子位置 (b) 新型SMO电机转子位置图11 转子位置变化曲线

根据图13与图14可知,在电机稳定运行时,新型滑模观测器下的电机转矩与电机三相电流畸变更小,在电机转速与电机负载产生突变时,电机转矩与电机三相电流能够在更短的时间内恢复稳定。

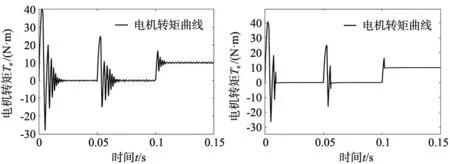
(a) 传统SMO电机转矩 (b) 新型SMO电机转矩图13 电机转矩变化曲线

根据图15可知,由于传统滑模观测器中采用符号函数作为切换函数,其不连续的特性导致电机扩展反电动势会产生抖动。新型滑模观测器下的反电动势有着更好的正弦性,从反电动势提取出的转子位置相关信息准确性得到明显提升。

(a) 传统SMO电机反电动势 (b) 传统SMO电机反电动势局部放大

综合上述仿真曲线可知,新型滑模观测器下的PMSM控制系统的动态响应特性与稳态响应特性都有着显著提升,整体系统具有更好的鲁棒性以及抗干扰性。

6 结论

本文针对目前永磁同步电机的无传感器控制方法中常用的传统滑模观测器算法进行了分析,同时对其进行了改进:

为了避免电机参数中的定子电阻的影响,将传统滑模观测器中的传统滑模面更换为积分滑模面;

为了削弱传统滑模观测器的抖振,将传统滑模观测器中的等速趋近律更改为指数趋近律与幂次趋近律结合的一般趋近律,同时将切换函数从传统滑模观测器中的符号函数更改为更为平滑的Sigmoid函数;

为了能够应对电机目标转速变化以及负载变化产生的影响,采用模糊控制系统,通过模糊控制系统对滑模观测器相关的函数参数进行调节。

利用MATLAB/Simulink仿真平台搭建电机控制系统的仿真模型,将新型滑模观测器与传统滑模观测器在同一条件下进行仿真,并将仿真结果进行对比。根据结果可见,与传统滑模观测器下的PMSM控制系统相比:

(1)在电机稳定运行时,新型滑模观测器下系统的转速误差、转子位置误差、电机转矩波动与电机三相电流波动更小,反电动势正弦性更强,系统的稳态响应性能更好。

(2)在电机转速突变时,新型滑模观测器下系统的电机转速、电机转矩与电机三相电流恢复稳定时间更短,转速误差变化幅度更小,系统的动态响应性能更好。

(3)在电机负载突变时,新型滑模观测器下系统的电机转速、电机转矩与电机三相电流恢复稳定时间更短,系统的抗干扰性更强。