基于折算齿形法的高阶非圆斜齿轮设计

刘 炀,宁少甫,胡绍东,李文波

(合肥工业大学机械工程学院,合肥 230041)

0 引言

非圆齿轮的设计方法主要有解析法、折算齿形法、包络法等[1-4]。解析法通过啮合角函数求解非圆齿轮的齿廓方程,其齿廓精度与齿廓采样点间距及数量有关,计算量较大。折算齿形法将每个轮齿位置处的节曲线近似为标准直齿轮分度圆,确定每点曲率中心并通过曲率半径的大小绘制对应的齿廓,其计算量较小,根据刘永平等[1]发现,解析法和折算齿形法的误差不超过2%,故折算齿形法对于非圆齿轮设计方面的广泛性较强。包络法模拟范成法加工齿轮的原理生成齿廓,其生成的齿廓精度和齿轮或滚刀刀具的精度及包络的步长相关,生成齿廓的过程较为复杂。

相比于圆柱斜齿轮,非圆斜齿轮同样拥有传动平稳、重合度大、承载能力强等特点。非圆斜齿轮的设计方法主要有两种:折算齿形法和包络法。前者是在此方法设计非圆斜齿轮端面的基础上,通过基圆半径参数和螺旋角确定每个齿的螺旋线,最终通过CAD建模完成非圆斜齿轮的建模并利用3D打印技术生成非圆斜齿轮[5-6];后者可以看作是非圆齿轮毛坯和滚刀刀具之间的切削运动生成非圆斜齿轮齿廓,通过非圆斜齿轮与滚刀刀具之间的啮合关系可以得到非圆齿轮的齿廓方程进而完成非圆斜齿轮设计[7]。二者方法各有侧重,折算齿形法设计思路简单,但三维建模重复性工作强,满足于精度较低的情况;包络法更侧重于制造生产,常用于要求精度较高的场合。

本文以折算齿形法为核心,详细梳理非圆斜齿轮的建模方法。同时,本文首次利用渐开螺旋面方程重新构造新的非圆斜齿轮“螺旋线”-截交线,完成建模。最后,对非圆斜齿轮模型进行运动学仿真,检查主、从动轮的啮合及干涉情况,以验证模型的合理性。

1 非圆齿轮的基本理论

1.1 非圆齿轮的节曲线相关参数设计

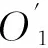
图1 主、从动轮节曲线

主、从动轮的节曲线极坐标表达式[8]分别为:

(1)

(2)

式中:n1、n2为主、从动轮的阶数,n为主、从动轮阶数的反比,n=n2/n1;k1、k2为主、从动轮偏心率,A1、A2为主、从动轮长半轴长。

当主动轮的基本参数确定时,从动轮的相关基本参数确定。主、从动轮的基本参数关系为:

(3)

(4)

(5)

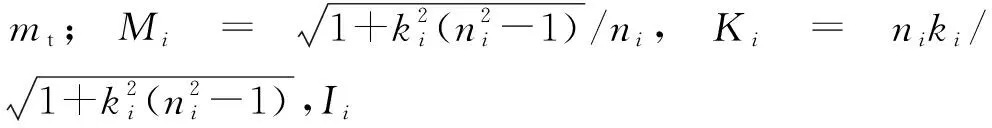
1.2 非圆齿轮的相关校验

非圆齿轮的校验包括压力角校验、根切校验和凹凸性校验[8]。三者的校验公式分别为:

(6)

式中:α为齿形角,i12为主、从动轮传动比函数,α12L为主动轮(i=1)逆时针转动时,左侧齿廓工作的压力角且保证α12L≤65°。

(7)

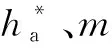
(8)

式中:ni=1时,齿轮为1阶椭圆齿轮,肯定无内凹。

1.3 非圆斜齿轮的螺旋线改进

在圆柱斜齿轮中,将齿廓曲面与分度圆柱面相交得到的螺旋线投影到分度圆所在平面上,螺旋线和分度圆重合。依据折算齿形法,在确定非圆斜齿轮的螺旋线时,需要计算每个轮齿位置处的曲率中心坐标及对应的分度圆半径,确定轮齿处的螺旋线。

1.3.1 非圆斜齿轮螺旋线的缺陷

由于每个轮齿处节曲线的曲率不同,对应的螺旋线偏向有所差异。如图2所示,将螺旋线投影至节曲线所在平面上,在节曲线ρ曲率较小处a1,螺旋线L1偏内;在节曲线ρ曲率较大处a2,螺旋线L2偏外。故由螺旋线生成的斜齿偏向不均,对非圆斜齿轮啮合性能影响较大,有必要对非圆斜齿轮螺旋线进行改进。

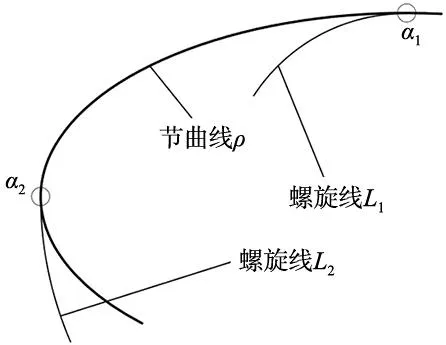
图2 投影面上螺旋线和节曲线关系示意图

1.3.2 渐开螺旋面的特点

如图3所示,在相对坐标系σ1x1y1z1上,当发生面KMN沿着半径为rb的基圆柱面Rb作纯滚动时,其上面的一条与基圆柱上母线JKN呈夹角为基圆柱螺旋角βb的斜直线KM展成的曲面ABCDE为渐开螺旋面,斜直线KM与基圆柱母线JKN的交点K形成的路径ABC为基圆柱螺旋线,且斜直线KM与基圆柱螺旋线ABC始终保持相切。

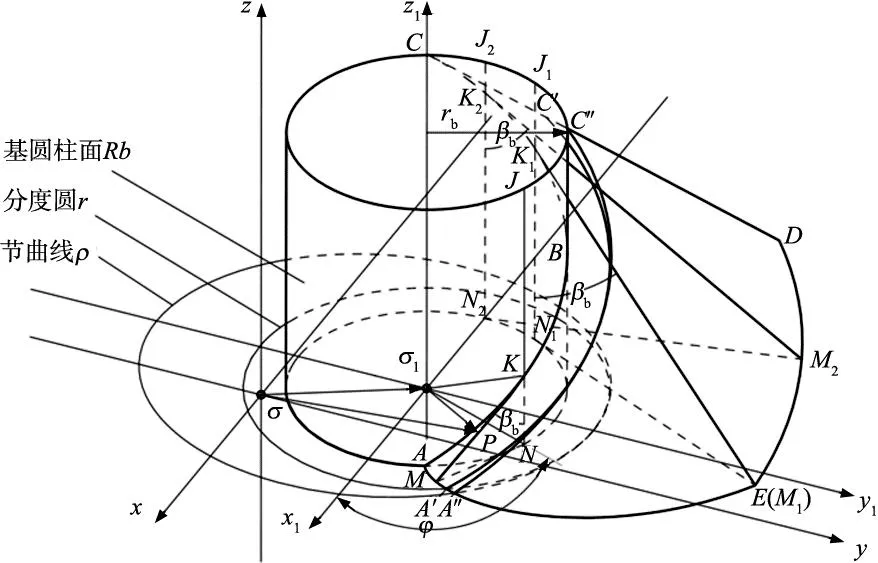
图3 渐开螺旋面形成原理

根据周建军、肖扬等[9-10]研究,以任意一个空间平面z1=C(C为任意常数)截取渐开螺旋面,则二者的交线为渐开线。对于圆柱斜齿轮,当C=0时,截得的渐开线AE即为斜齿轮端面的渐开线;C=B(B为齿宽)时,截得的渐开线是斜齿轮另一端面的渐开线。基圆柱对应分度圆r形成的柱面和渐开螺旋面ABCDE截得的空间曲线A′C′即为斜齿轮的螺旋线。

在相对坐标系σ1x1y1z1上,渐开螺旋面的曲面参数方程为:

(9)

式中:p=rbtanβb,βb为基圆柱螺旋角,rb=σ1N为基圆半径,φ为发生面KMN在基圆柱上滚动时,其与基圆柱相交的切线KN在基圆柱上划过的角度;PK=u,由基圆柱螺旋线ABC与PK的切点K到渐开螺旋面上任一点P的线段;KN=pφ,螺旋上升运动中转过角度φ时切点K上升的距离。

1.3.3 非圆斜齿轮的螺旋线求解

为克服非圆斜齿轮的螺旋线偏向不均问题,拟确定一节曲线柱面,使其与渐开螺旋面ABCDE相交,截得的交线为空间曲线A″C″,其不再是螺旋线,称此曲线为截交线,之后不再赘述。将截交线A″C″投影至节曲线所在平面上,其与节曲线重合,解决了螺旋线偏向不均问题。下面将对截交线A″C″进行求解,求解步骤为:

步骤1:依据图3,将绝对坐标系σxyz固定在非圆斜齿轮回转中心O,将相对坐标系σ1x1y1z1扩展为σjxjyjzj(j代表轮齿标号,即第j个轮齿)并固定在非圆斜齿轮端面处轮齿的曲率中心cj处。

步骤2:求得第j个轮齿对应处的曲率中心在坐标系σxyz中的向量表示。

设节曲线上第j个轮齿处对应的极坐标为(θj,ρj(θj),0),通过变换得到曲率中心cj在绝对坐标系σxyz下的坐标cj(=σσj)为:

(10)

(11)

式中:rj(θj)表示第j个轮齿处的曲率半径,nj(θj)表示第j个轮齿处的法线方程倾斜角。

同理可求得其他轮齿得其他轮齿的曲率中心坐标得到曲率中心坐标集合矩阵C3×z=(c1…cj…cz),其中z为齿数且j≤z。

步骤3:根据式(9)参数方程求其向量形式,即所求的第j个轮齿处渐开螺旋面(ABCDE)j的向量方程表示为:

pj=σjP=(xj(φj),yj(φj),zj(φj))T

(12)

其参数方程形式为:

(13)

式中:pj=rbjtanβb,rbj为第j个轮齿对应的基圆半径。

同理可求得其他轮齿渐开螺旋面的向量集合矩阵P3×z=(p1…pj…pz)。

步骤4:将第j个轮齿处的渐开螺旋面(ABCDE)j在绝对坐标系σxyz中表示并写出节曲线柱面方程。

依据图3,渐开螺旋面(ABCDE)j在绝对坐标系σxyz中表示为:

oj=σP=cj+pj

(14)

根据式(10)～式(14),oj具体表示为:

(15)

其函数形式为:

Fj(xj(θj,φj,uj),yj(θj,φj,uj),zj(φj,uj))=0

(16)

经过上述分析,所有的渐开螺旋面的向量集合矩阵O3×z=(o1…oj…oz)表示为:

O3×z=C3×z+P3×z

(17)

又根据式(1),平面节曲线ρ(θ)的直角坐标柱面方程为:

(18)

其函数形式为:

F(x(θ),y(θ),z(θ))=0

(19)

可通过式(18)计算出轮齿在节曲线处的直角坐标为T3×z=(t1…tj…tz)。

将式(16)和式(19)化简并联立得到第j个轮齿的截交线一般方程Gj(θj,φj,uj,θ,ρ(θ))为:

(20)

G=(G1…Gj…Gz)

(21)

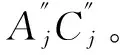
2 高阶非圆斜齿轮的建模过程

2.1 非圆斜齿轮的基本参数设置

非圆斜齿轮主动轮的主要参数如表1所示。从动轮的相关参数需要根据主动轮参数及凹凸性校验确定从动轮的阶数n2,偏心率k2、z2和中心距a。

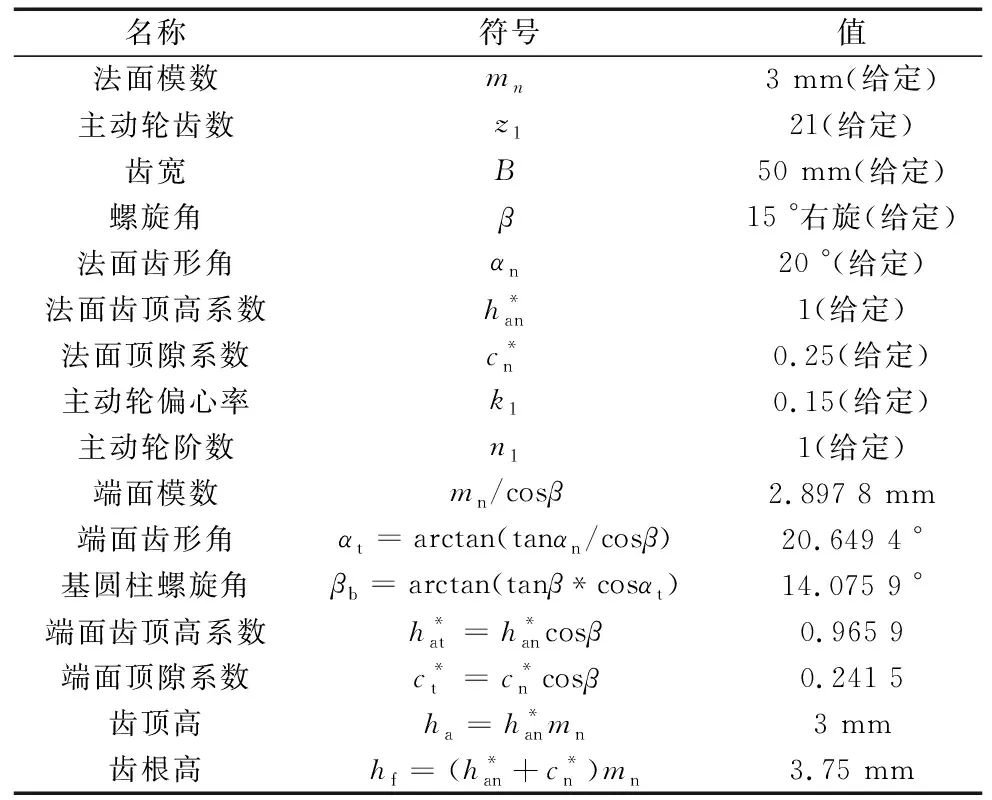
表1 主动轮基本参数表

从动轮无内凹的最大阶数n2为[8]:

(22)

式中:floor()函数为向下取整函数。

经式(22)计算得到n2max=6,选择适中的计算量,确定从动轮阶数为n2=3。

通过式(2)计算得到从动轮偏心率k2=0.050 508。

通过式(3)计算得到中心距a=130.197 mm。

根据式(4)求得的节曲线周长满足关系I2=n2I1,故为使从动轮齿数z2均布于整个节曲线周长,其齿数满足z2=n2z1=63。从动轮的参数如表2所示。

表2 从动轮基本参数表

2.2 轮齿的位置确定

对于非圆斜齿轮,由于其节曲线曲率半径不相等,啮合的轮齿必须一一配对,确保非圆斜齿轮的正常运转。

根据吴序堂等[8]研究,当齿轮的阶数ni=1时,齿轮齿数zi一般设计为奇数,规定主动轮节曲线长轴的一端应为轮齿,所对的另一端应为齿槽,从动轮相反;当齿轮的阶数ni=2时,齿轮齿数zi应满足zi=4C+2(C为正整数);当ni>2时,齿轮齿数zi=niC1(C1为奇数)。根据图1所示,在啮合过程中,起始啮合处应从图1处的节曲线相切处开始计算。最终,轮齿的位置分布如图4所示,“·”点代表轮齿位置。

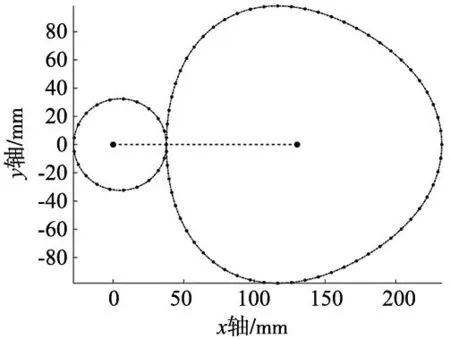
图4 主、从动轮的轮齿分布图

2.3 计算曲率半径及曲率中心位置

通过式(7)、式(10)和式(11)可分别计算出每个轮齿对应的曲率半径R1×z=(r1…rj…rz)和曲率中心坐标矩阵C3×z=(c1…cj…cz)。图5展示了在转动一周的过程中,主、从动轮的曲率半径变化,图5中“·”点代表以确定轮齿位置处的曲率半径。

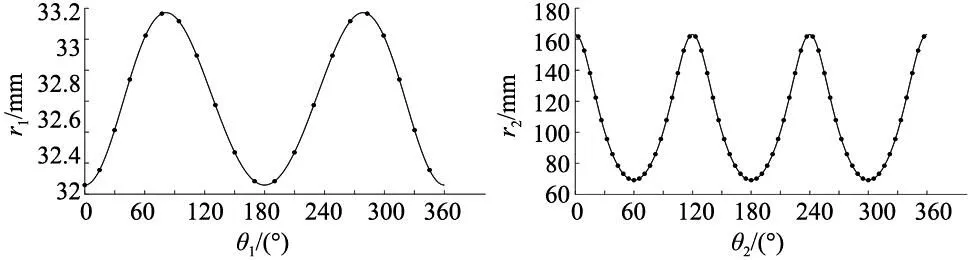
(a) 主动轮曲率半径化图 (b) 从动轮曲率半径变化图图5 曲率半径变化图

如图5所示,主、从动轮曲率半径呈周期性、对称性变化。可根据此变化对齿廓进行对称操作以增加非圆斜齿轮建模效率。

2.4 计算其他参数

RB1×z=R1×zcosαt

(23)

(24)

(25)

(26)

由于在2.5节建模环节通过方程式绘制渐开线时,渐开线的展角起点是轮齿中心处,并未在齿根处,故通过式(24)计算其旋转角度,根据渐开线的展角方向确定其旋转方向。

在建模环节中,端面齿廓沿着截交线进行路径扫掠时,需要扭转角度以避免其端面渐开线齿廓形状变化。主动轮(i=1)是右旋,扭转角度为正;从动轮(i=2)是左旋,扭转角度为负。

2.5 非圆斜齿轮建模

将表1、表2及上述计算涉及的相关参数在excel中进行整合,利用中望3D的批量提取变量操作,将数据导入,完成建模前的准备工作。

2.5.1 相关曲线的绘制及坐标点、直线的绘制

将数据导入中望3D后,依次点击“线框-曲线-方程式”,输入节曲线方程,由于节曲线相关参数已导入,直接输入式(27)并点击确定即可。

(27)

通过偏移命令,分别绘制齿顶曲线和齿根曲线,偏移量分别为ha(向外)和hf(向内)。应再绘制一条基准为齿根曲线、偏移量足够小(0.5 mm)向内的布尔曲线,以便建模最后实现齿根曲线拉伸操作时可实现布尔加操作。

通过点的绘制命令,在其变量浏览器中分别选择曲率中心坐标C3×z=(c1…cj…cz)和轮齿心坐标T3×z=(t1…tj…tz),完成相关点的绘制。最后绘制所有对应两点(cj,tj)控制的直导线集合L,其结果如图6所示。

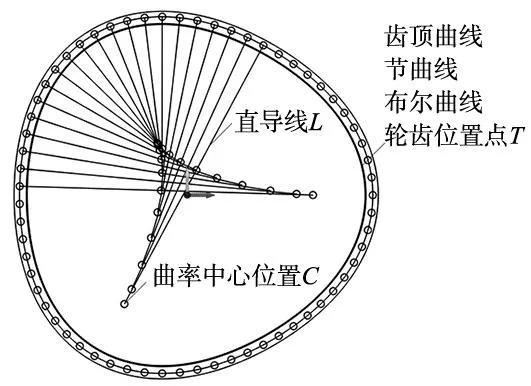
图6 从动轮相关点、线的绘制

2.5.2 渐开螺旋面绘制及截交线、渐开线的获取

根据图3,渐开螺旋面的形成的主要几何曲线包括基圆柱螺旋线ABC和斜直线KM,其绘制过程步骤为:

步骤1:绘制轮齿基圆柱螺旋线集合HLrb。绘制基圆柱螺旋线时,选择轮齿对应轴位置(曲率中心位置C)、对应起点(轮齿位置T)、对应基圆半径(RB)螺旋线高度(S/2)和螺距(S),完成基圆柱螺旋线绘制。

步骤2:绘制斜直线KM集合OL所在草绘平面集合PF。以基圆柱螺旋线远处端点为定位点,以对应直导线集合L所指方向为平面z轴(平面法线方向),完成建立定位点处基圆柱螺旋线的切平面集合PF,单个轮齿切平面绘制如图7所示。

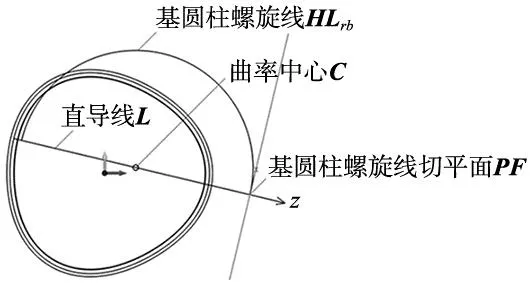
图7 单个轮齿处基圆柱螺旋线、切平面的绘制

步骤3:绘制斜直线KM集合OL。以步骤3绘制的切平面集合PF为草绘平面,再以基圆柱螺旋线远处端点为起始点绘制斜直线KM,使其与基圆柱螺旋线相切,斜直线长度适中,最终的绘制效果如图8所示,其夹角为基圆柱螺旋角βb数值,验证了绘制方法的正确性。

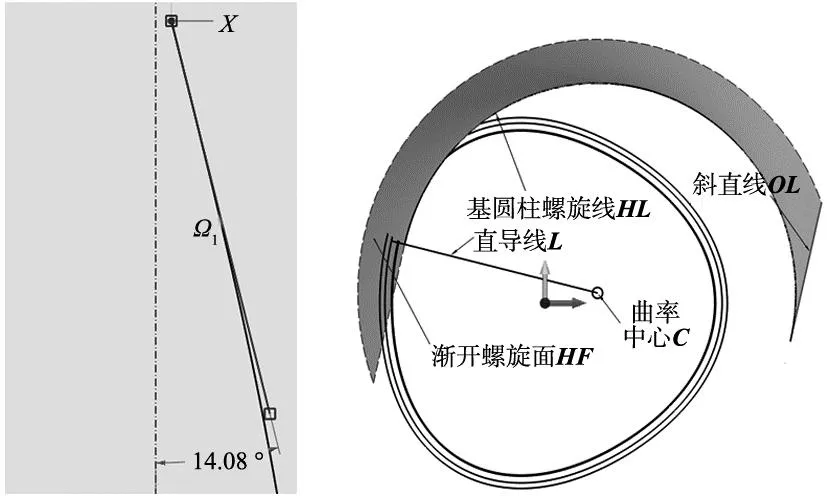
图8 单个螺旋线斜直线KM 图9 单个渐开螺旋面绘制

步骤4:绘制渐开螺旋面集合HF。以斜直线KM集合OL为轮廓,以对应基圆柱螺旋线集合HLrb为路径进行扫掠得到渐开螺旋面集合HF,其单个渐开螺旋面绘制效果如图9所示。

步骤5:截取渐开螺旋面集合HF至齿宽B内,拉伸节曲线为曲面,节曲线柱面和渐开螺旋面集合HF的相交曲线即为1.3节所求的截交线G。底平面与渐开螺旋面集合HF的相交曲线即为端面一侧的渐开线,如图10所示。

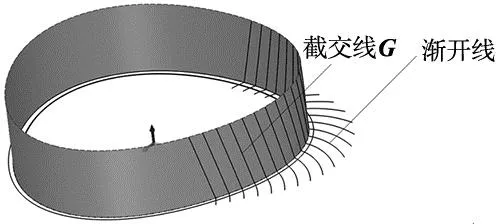
图10 截交线、渐开线的获取

2.5.3 端面齿廓及斜齿的绘制

对曲率中心坐标C建立局部坐标系,令x轴指向其对应直导线L方向。建立轮齿处节曲线的法平面SF。在此坐标系上对生成的左侧渐开线旋转ROT1角度并镜像对称,镜像面为SF,生成完整的渐开线绘制。最后对其进行修剪,完成渐开线齿廓INV的绘制,如图11所示。

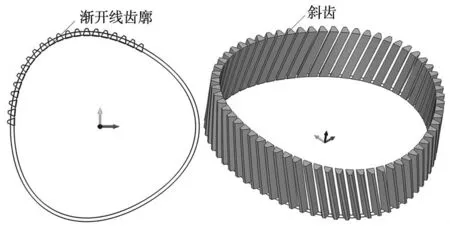
图11 渐开线齿廓 图12 斜齿的绘制

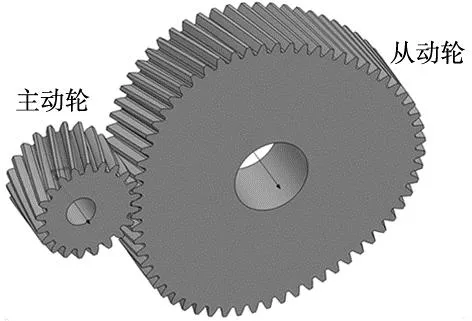
图13 主、从动轮模型

以渐开线齿廓INV为扫掠轮廓,以截交线G为扫掠路径,以ROT2为扭曲角度,生成扫掠实体,最后进行多边形阵列,生成完整的斜齿。

2.5.4 非圆斜齿轮的收尾工作

以节曲线进行拉伸,拉伸长度为齿宽B,执行布尔加运算,使其与斜齿成为整体。最后对齿根处倒圆角并进行多边形阵列,绘制轴孔,完成高阶非圆斜齿轮的建模,主动轮建模同方法。

3 运动学仿真分析

建模完成后需要对非圆斜齿轮进行运动学仿真分析,以检查非圆齿轮副是否干涉及满足要求的变传动比传动。将中望3D建立的模型导入Creo中,并按照要求添加转动副及相关约束,完成主、从动轮的装配。由于非圆斜齿轮传动比呈函数形式,无法使用一般齿轮副进行连接,故拟对主、从动轮分别添加不同的伺服电动机作为驱动源,使主、从动轮按照各自的电机参数进行转动,并检查此过程中的干涉情况[11]。设置主动轮为转速为ω1=60 °/s,即主动轮按照此转速匀速转动;从动轮转速应按照式(28)进行计算,即根据传动比函数i12及ω1,从动轮按照函数形式进行转动。

(28)

驱动源设置完成后运行,并利用Creo的全局碰撞检测功能对运行数据进行分析,当齿轮副啮合区域出现红色区域时,即发生干涉。在对非圆斜齿轮进行运动仿真分析时,发现其整体运转性能良好,但部分轮齿出现颜色区域,即模型存在微小的干涉情况,需要解决干涉问题。

对于非圆齿轮,解决干涉的方法主要有修正齿形和调整中心距等。本实例通过适当调整中心距解决了干涉问题。相比标准中心距a=130.197 mm,调整后的中心距a′=130.658 mm能完全规避干涉问题,其中心距增量不超过0.36%,满足大部分应用场合。

4 结论

(1) 由于绘制非圆斜齿轮的参数数量过多,需要利用MATLAB的强大计算功能处理其相关参数,再利用中望3D的excel参数批量导入操作,大大节省非圆斜齿轮的绘制时间;

(2)本文采用渐开螺旋面和节曲线柱面的相交曲线(截交线)替代传统的轮齿螺旋线,有效地解决了传统螺旋线因偏向不均问题,一定程度上减少轮齿的干涉率并增强其重合度。通过推导证明了截交线的合理性,并通过建模证明其可行性;

(3)针对非圆斜齿轮进行CAD建模时,详细描述了基于折算齿形法的高阶非圆斜齿轮建模过程,对于大部分非圆斜齿轮和非圆直齿轮建模有重要的借鉴意义;

(4)利用Creo的全局碰撞检测装置检查非圆斜齿轮的干涉情况,通过调整中心距解决其干涉问题,其调整增量不超过0.36%,证明模型满足大部分应用场合,对于后期研究非圆斜齿轮的啮合刚度有重要意义。