基于3D相机的拆垛机器人手眼标定方法研究

郭 源,张爱军

(南京理工大学机械工程学院,南京 210094)

0 引言

近年来,随着机器人技术与机器视觉技术不断地革新,催生了许多形态各异的机器人[1]。其中,拆垛机器人是通过视觉引导定位抓取目标物的一类机器人。拆垛机器人由机械臂、相机以及计算机设备组成,先由相机对目标垛堆进行图像采集,再由计算机设备对采集的数据做物体姿态估计,最后将位姿结果反馈至机械臂,由机械臂进行抓取[2]。其中,手眼标定是机械臂抓取中的重要一步,手眼标定技术的准确性直接影响了目标物抓取准确性[3]。所以,改善拆垛机器人的手眼标定关键技术,是整个拆垛系统的准确度的关键所在。

业界对手眼标定有许多研究成果。如TSAI等[4]首次提出了手眼标定方程AX=XB,并利用线性二分法来进行解算,但在求解旋转向量时易引入较大的误差。DANIILIDIS[5]提出基于对偶四元数改写手眼方程,但在实际标定中易受到噪声的干扰,影响标定的准确度。基于此,TABB等[6]使用迭代算法进行手眼标定的求解。但迭代求解过程复杂且依赖初值,才能有较为精确的结果。王一凡等[7]利用对偶四元数的最小二乘法进行迭代。李巍等[8]采用了LMI优化算法,结合对偶四元数求出刚性变换矩阵,但是利用LMI算法求解矩阵依赖于问题参数模型的选取及相关工具箱,算法复杂不易工程化。在数据获取方面,YANG等[9]使用标定球来获取标定数据,但标定球制作不易。王连庆等[10]设计了一种标定块,利用点云匹配算法来获取转换关系,虽然利用点云算法会更为精确,但点云运算耗时过长。程麒等[11]利用标定板对龙门架机器人进行手眼标定,但其轨迹规划及去噪处理不适用于拆垛机器人,故需对其进行改进。

综上所述,为了提高拆垛机器人的精度,提出一种基于对偶四元数和3D相机的手眼标定方法。刘屹东等[12]利用粒子群对相机参数进行标定,证明其在标定领域可进行非线性优化,故本文将其运用在手眼标定方面。并采用自适应粒子群算法避免手眼标定求解过程陷入局部最优值,在数据获取方面,采用普通的圆形标定板,并利用加权奇异值分解算法提高算法稳定性。经检验该方法具备较高的准确度,可以用于拆垛机器人的定位抓取工作。

1 手眼标定问题描述和求解

1.1 手眼标定方程构建

拆垛机器人进行拆垛工作时需要先获取机器人基座坐标系和相机坐标系之间的位置关系,对此刚体转换矩阵的获取过程即手眼标定。手眼标定问题分为眼在手上和眼在手外,眼在手上即相机固定在机械臂末端,此方法拥有较高的精度,可用于焊接、自动化贴片等。眼在手外即相机被固定在机械臂外某一位置,有较广的视场,虽然精度较低,但可用于机器人大范围抓取等领域。故拆垛机器人较为适合选用眼在手外的拆垛系统进行工作。

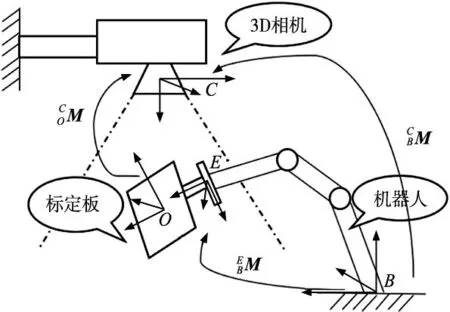
图1 拆垛机器人眼在手外标定模型

已知对于每张图片,都有以下关系:

(1)

由式(1)结合机械臂变换情况可推导出式(2):

(2)

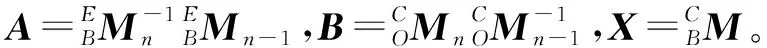
AX=XB

(3)

式中:A可以有机械臂的示教器获得,B可以由相邻点云标定板的变换矩阵求得。因此,求解手眼标定方程的解,即是对X进行求解。

1.2 传统的对偶四元数算法

为了构建目标函数以供解算,可根据手眼标定方程AX=XB,将其分解为旋转和平移两部分:

RARX=RXRB

(4)

(RA-I)tX=RXtB-tA

(5)

式中:R为旋转矩阵,t为平移向量,I为单位矩阵,下标表示它们所对应的齐次矩阵。

由于采用对偶四元数可以用两个四元数同时描述旋转和平移部分,避免了万向节死锁。故根据文献[5]引入对偶四元数进行手眼标定方程的模型构建与解算。

对偶四元数是四元数的对偶形式,可以将其表示为:

(6)

(7)

根据式(7),可将式(4)和式(5)变形为对偶四元数形式:

a·qx=qx·b

(8)

(9)

(10)

对该方程进行解算即可求得手眼标定的对偶四元数解。

1.3 基于自适应粒子群的手眼标定改进算法

由于传统的对偶四元数解算法易受噪声干扰引入旋转误差,故本文使用粒子群优化算法,将对偶四元数的旋转部分和平移部分分开解算,避免3D相机带来的平移误差对旋转部分的影响。

粒子群算法是一种出色的全局搜索策略算法,可以用于工程实践之中,能有效解决非线性函数寻优问题。粒子群算法将诸多粒子当做鸟类,并赋予各个粒子初速度vi和初位置xi。每个粒子经过速度和位置的变换,会不断地更新个体极值Pbest,i,并与其它粒子共享,并经过比较得出群体极值Gbest,通过个体极值与群体极值进行比较,各个粒子将会通过式(11)和式(12)进一步进行迭代,直到获得最终的全局最优解。

vi(k+1)=ωvi(k)+c1r1(Pbest,i(k)-xi(k))+
c2r2(Gbest-xi(k))

(11)

xi(k+1)=xi(k)+vi(k+1)

(12)

式中:r1、r2为(0,1)内的随机数,ω为惯性权重,c1、c2为学习因子,c1引导粒子向个体极值方向飞行,而c2引导粒子向群体极值方向飞行。由于标准的PSO(粒子群)算法易陷入局部最优解,且需要设置诸多参数,故在应用中受到了限制。基于此,需要对标准PSO算法进行改进,使其更为适应手眼标定方程的求解。

其中,惯性权重ω的值与粒子的搜索能力有直接的关联,ω的值越大,则粒子的全局搜索能力越强,反之则粒子的局部搜索能力越强。为了平衡粒子的全局寻优能力和局部寻优能力。可采用正弦曲线函数,在粒子寻优的前期,赋予较大的ω,使粒子进行大范围搜索。在寻优后期,使粒子更注重局部搜索,因此可使用正弦惯性权重函数:

ω=ωmax-(ωmax-ωmin)sin(tπ/(2Niter))

(13)

式中:ωmax取0.9,ωmin取0.45,t为当前迭代次数,Niter为总迭代次数。

同理,为了增强前期全局寻优能力和后期局部寻优能力,可将学习因子c1、c2进行改进,采用闫群民等[13]提出的方法,使c1逐渐减小、c2逐渐增大。

c1=c1max-t(c1max-c1min)/Niter

(14)

c2=c2min-t(c2min-c2max)/Niter

(15)

式中:c1max、c2max为2.5,c1min、c2min为1.25。

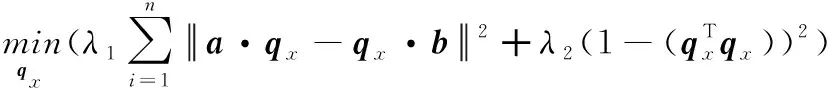
(16)

同理,将模型1的解算结果代入,利用平移矩阵的性质,最终可得到平移矩阵的求解模型:

(17)

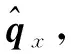
2 手眼标定数据的预处理

2.1 手眼标定数据的获取及轨迹规划

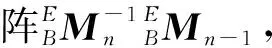
但与点云坐标系相关的数据需要通过对标定板进行多次移动,通过采集标定板圆心点坐标的变换量进行计算。为了获取不同方位下标定板的数据,以及配合3D视觉相机下的锥形视野,故提出3层梯状采样法来获取相关数据。为了获取标定板的角度信息,可在点Q处,进行5次以上不同方向的旋转,每次旋转角度不低于30°。标定板移动轨迹如图2所示。

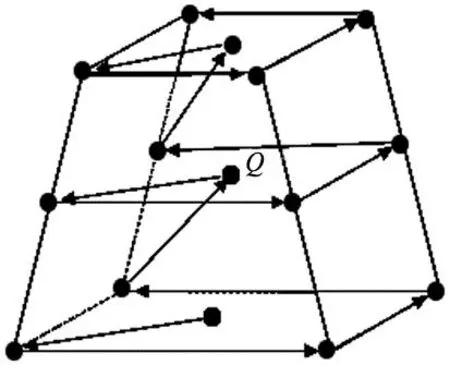
图2 标定板的3层梯状移动轨迹

2.2 标定板圆心的点云坐标获取

采用标定块进行标定点提取的方法在三维标定邻域十分热门,但标定块制作不易,成本高昂,对于拆垛机器人只需使用抗噪性强的4×5圆形标定板进行圆心点云坐标提取,可以显著降低成本,标定板如图3所示。

图3 点云中标定板圆心提取效果

本文使用3D结构光相机。通过3D相机提供的深度信息,便可以由图片生成点云,并获取图片中任意像素点的三维坐标。利用这一性质,可利用Opencv提取出二维状态下圆形标定板的圆心坐标,再通过深度值则可计算出三维坐标下圆心的坐标值。其标定板点云圆心提取效果如图3所示。

2.3 基于IGGⅢ的加权奇异值分解算法

(18)

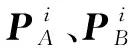
(19)

(20)

令U为左奇异矩阵,V为右奇异矩阵,W为对角系数权重矩阵,则由SVD分解可得:

[U,S,V]=SVD(AWBT)

(21)

则旋转变换矩阵R为:

R=VUT

(22)

平移矩阵为:

t=-R*CA+CB

(23)

至此,便可初步得到标定板点云间的变换矩阵。为了追求计算简便,普通的SVD方法只是将权重值都设为相同值。但是使用标定板的缺点便是易受光照及相机畸变所影响,导致提取的部分圆心坐标不准确,为此有必要引入合适的加权函数来进行降噪,增加算法的稳定性。

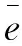
(24)

根据各点的测量误差并结合实际情况,可选取加权函数IGGⅢ来进行权重系数的计算,该函数满足误差小的点位权重保持不变,误差稍大的点位降低权重分配,而误差较大的点位权重置0,该函数的表达式如下:

(25)

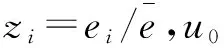
3 实验结果与分析

本文使用如图4所示的拆垛机器人手眼标定系统对本文提出算法进行验证。在CPU为Intel(R) Core(TM) i5-8300H,内存为16 G的主机上进行运行。

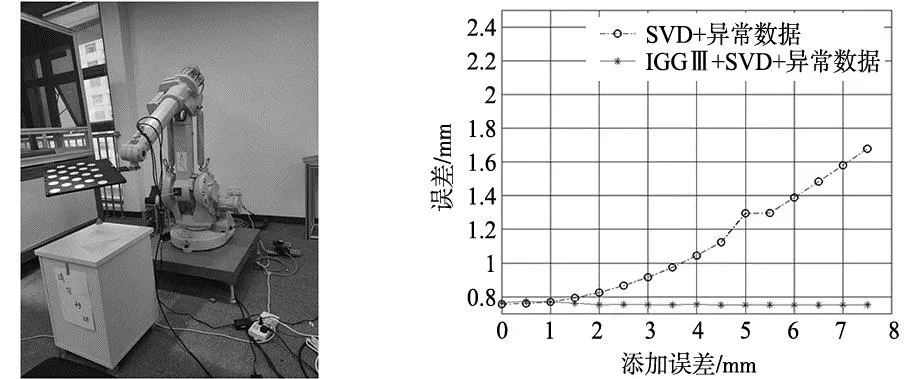
图4 眼在手外标定系统 图5 SVD与IGGⅢSVD方法比较

该系统按照上述方法进行手眼标定,每组实验使用标定板在20个方位上采集20张照片及其对应点云,并获取20组机械臂末端位姿。

为验证加权SVD算法的有效性,实验中选择一组标定板的点云坐标变化数据,共20个点位。任取20%,随机选择X或Y坐标赋予0～7 mm的误差模拟光照等因素对标定板的影响,分别采用SVD算法和加权SVD算法进行验证,可以看出加权SVD算法对粗大误差的抑制效果较好,结果如图5所示。

(26)

用3种算法分别在不同噪声水平下进行200次模拟计算,可得到不同高斯噪声水平下的误差。可以看出,本文算法在不同高斯噪声条件下保持着较优的精度,如图6所示。

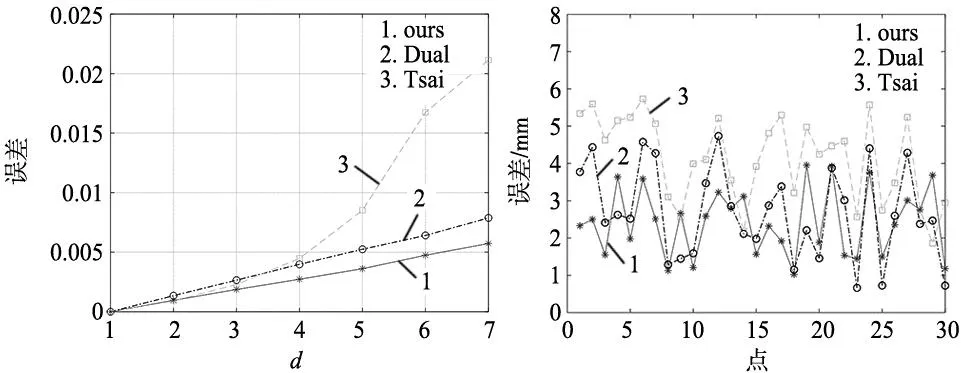
图6 不同噪声水平下的误差曲线图 图7 不同点位的误差曲线图

后续经过实际实验计算,可以得出最优的一次手眼标定矩阵Xbest,即:

为了增加实验结果的可靠性,本文提出一种误差验证方法,仿造图2所示的标定过程中标定板的移动轨迹,将标定板放置在三层平面上,并将标定板分别放置在每层平面的5个方位由机械臂末端对圆形标定板的对角圆心碰触,以获取标定板在不同方位的准确坐标。再由所获取的点云坐标以及计算得出的刚体变换矩阵X,来计算得出标定板在基座坐标系下的理论坐标pmath,将其与实际坐标ptrue进行误差计算,便可得到刚体变换矩阵的准确性。计算投影误差如式(27)所示。

(27)

实验结果表明,Tsai法的平均精度为4.135 4 mm,Dual法的平均精度为2.677 4 mm,本文所提方法的平均精度为2.421 4 mm,小于2.5 mm,最大误差为3.9 mm,不超过4 mm,满足拆垛要求,平均精度高于其余两种方法。

4 结论

本研究采用对偶四元数对手眼标定进行模型构建,利用三层梯状采样法和加权SVD算法得到了鲁棒性较强的待处理数据,而后采用自适应粒子群算法得到了较优的手眼标定结果。

实验结果表明,加权SVD算法在获取手眼标定数据中具备较强的鲁棒性,而且使用自适应粒子群算法求解手眼标定方程的平均精度高于Tsai法、略优于Dual法,最终结果的平均误差小于2.5 mm,且所提的算法在本文所述的模拟环境下,赋予其不同水平的高斯噪声时,有较好的稳定性。对于同类型拆垛机器人的手眼标定工作具有一定的参考价值。