基于即插即用框架的脉冲噪声图像复原算法
梅金金
(阜阳师范大学 数学与统计学院,安徽 阜阳 236037)
引言
图像复原是图像处理研究中不可或缺的一个步骤,被广泛地应用于计算机视觉处理、压缩感知、医学成像和高光谱遥感成像等诸多领域。图像在采集和传输过程中经常会出现一定的模糊、失真以及受到各类噪声的污染,这就导致图像的清晰度受到严重的影响。近年来,很多学者提出了经典的图像复原算法。比如,Tikhonov 正则化模型可以有效地去除图片的噪声,但是随着去噪效果逐渐增强,会导致图片的边缘信息越来越模糊[1]。为了在去除噪声的同时保留图像的边缘信息,基于全变分(Total Variation,简称TV)的ROF模型引起了广大学者的关注,但复原图像中出现一定程度的阶梯效应[2]。为抑制去噪图像中的阶梯效应,学者在TV 正则的基础上进行改进,陆续提出了高阶全变分(Higher Degree Total Variation,简称HOTV)[3]、广义全变分(Total Generalized Variation,简称TGV)[4]、非局部全变分(Nonlocal Total Variation,NLTV)[5]、分数阶全变分(Fractional Order Total Variation,简称FOTV)[6]与交叠组合稀疏高阶全变分(Overlapping Group Sparsity Total Variation,简称OGSTV)[7]等。这些正则化方法在一定程度上抑制了TV 所引起的阶梯效应,但图像复原算法还有进一步提升的空间。Kostadin 等人根据图像块之间的相似性,结合空域思想和转换变换的方法提出BM3D 算法,以此来提升图像的去噪复原效果[8]。Gu 等人提出的加权核范数最小化方法(简称WNNM),结合矩阵奇异值稀疏性与核范数权重,有效利用测试图像的相似结构,但算法运行需要耗费大量的时间[9]。Zhang 等人结合卷积神经网络方法提出将噪声图作为网络输入的FFDNet 算法,其训练时间短、迭代次数小,而且能处理不同噪声水平及空间变化的噪声[10]。
因此,根据以上各类去噪算法的优势,我们提出一个新的基于Lp 保真项的数学优化模型[11],能够保证在去除脉冲噪声的同时更多地保留图像的细节信息。同时,结合即插即用算法框架的特点[12,13],利用变量分离算法将目标函数解耦为保真项与正则项,为利用基于FFDNet 去噪器提供了可能性。然后,应用交替方向迭代算法求解所提出的数学模型,并对算法进行加速处理。数值上,与L1 保真项的模型算法相比,改进方法获得的复原图像视觉效果更好,在量化指标上也具有一定的优势。
1 脉冲噪声
针对脉冲噪声下的图像复原问题,图像退化模型可以表示为
其中f∈Rmn为模糊图像,u∈Rmn为原始图像,K为模糊算子,N(·)为脉冲噪声。这类噪声包含椒盐噪声和随机值噪声,具体如表1 所示。

表1 脉冲噪声类型
其中fmin,fmax表示退化图像f所有像素值的最小值与最大值,θ是均值等于0 服从正态分布的随机变量。
2 模型建立
近年来,学者们已经开始广泛关注脉冲噪声下的图像复原问题。研究表明,L2 范数下的保真项会使得复原图像中出现大量的伪同心圆,不适用于消除脉冲噪声。L1 范数下的保真项符合脉冲噪声的统计学特性,可以很好地抑制脉冲噪声。因此,在文献[14]中,Nikolova 等人结合TV正则项和L1 数据保真项提出一种新的凸优化模型,其离散形式表示如下:
其中‖ ‖·1表示向量1 范数,∇表示梯度算子,‖ ∇u‖1表示TV 的离散形式,μ>0 表示正则参数,起到调节TV 正则项与L1 数据保真项的作用。同时,我们把上面的模型简称为L1TV 模型。在文献[15]中,利用Lp 非凸保真项解决稀疏信号复原与矩阵补全问题,验证Lp 保真项比L1 保真项的复原结果更好。
因此,为了利用图像的相似性和神经网络方法,提高图像的复原效果,我们提出了一种新的去除脉冲噪声的数学优化模型:
其中Re(u)表示隐式的去噪器,可以应用KSVD[16],non-local means[17,18],BM3D[8],WNNM[9],FFDNet[10]等去噪器。
3 模型求解
根据非凸问题下ADMM 算法[19]的收敛性质和即插即用算法框架[12,13]的优点,我们考虑利用该算法求解模型(3)。首先,引入两个新的变量v,z∈Rmn,将(3)式转化为如下离散约束非凸模型:
令λ1为约束条件v=u的Lagrange 乘子,λ2为约束条件z=Ku-f的Lagrange 乘子,则可得到共增广的Lagrange 函数:
其中β1,β2是大于0 的罚参数。因此,求解的数学模型(3)式的ADMM 算法归纳总结如下:

为计算v-子问题,我们考虑利用基于学习的隐式去噪器,具体计算公式表示如下:
其中D(·)为去噪器算子。为了深度提取图像的特征信息,同时考虑到运行时间和计算的复杂度,我们在数值实验中仅采用BM3D[8]和FFDNet算法[10]进行去噪处理。
同时,对于z-子问题,令tk=(Kuk-f)-,则上述问题可写为
上述问题是一个Lp 范数优化问题,它的极小值点可以利用Lp 范数的近端算子[15]表示,具体计算公式为:
针对u-子问题,我们求解它的Euler-Lagrange 方程,即
经过简单的整理后,上述方程可转化为
在周期边界条件下,考虑利用快速傅里叶变换求解,即:
其中F,F-1分别表示快速傅里叶变换与逆傅里叶变换。
为进一步加快算法的收敛速度,我们考虑利用FISTA 算法[20,21]对z-子问题加速。结合上述三个子问题的计算,加速的PnP-Lp 算法可以详细整理如下:

4 数值实验
本文通过一些数值实验展示所提出的数学模型与算法在去除脉冲噪声的有效性。以灰度图像Boat 为测试图像(如图1 所示),像素值均映射到数值范围[0,1]。同时,为了验证所提出模型去除脉冲噪声的有效性,我们将基于Lp 保真项的算法PnPBM3D-lp、PnPFFDNet-lp 与基于L1 保真项的算法PnPBM3D-l1、PnPFFDNet-l1 做对比。数值实验是在Matlab R2021a 的编程环境、CPU2.80 GHz Inter Core 处理器和内存为8GB 的台式计算机。

图1 测试图像
在实验过程中,为客观评估复原图像的质量,我们考虑如下两个度量标准:峰值信噪比(Peak Signal-to-Noise Ratio,简称PSNR)和结构相似度(Structural Similarity Index Measurement,简 称SSIM)[22]。峰值信噪比的计算公式表示如下:
其中μu,σu是原始图像u的均值和标准差,μuˉ,σuˉ是复原图像-u的均值和标准差,c1,c2是大于0 的常数,σu-u是u与uˉ的协方差。当结构相似度越趋向等于1,说明复原图像与原始图越相似。
对于算法2,设置参数在0 到1 范围之内,参数μ,β1,β2的选择对复原结果有着很大的影响。为获得更好的图像复原结果,获得最大的PSNR 值,手动调整参数μ,β1,β2。对于z-子问题,涉及到计算变量的牛顿内迭代算法,将其迭代次数设为5。对于算法的收敛性,以30%的椒盐噪声、高斯模糊下的退化图像为实验对象,给出这四个算法的PSNR 值与复原结果的相对误差随着迭代次数变化的曲线图,其中复原图像的相对误差计算公式表示如下:
根据图2 所示,这四种算法的PSNR 值整体上呈现递增趋势,在迭代次数达到30 次时逐渐趋向于平缓。再考虑到算法所需要的CPU 时间,所有算法的迭代次数均设为30。同时,随着算法迭代次数的增加,复原图像的相对误差逐渐降低直至趋于稳定,这说明算法在数值实验上是收敛的。
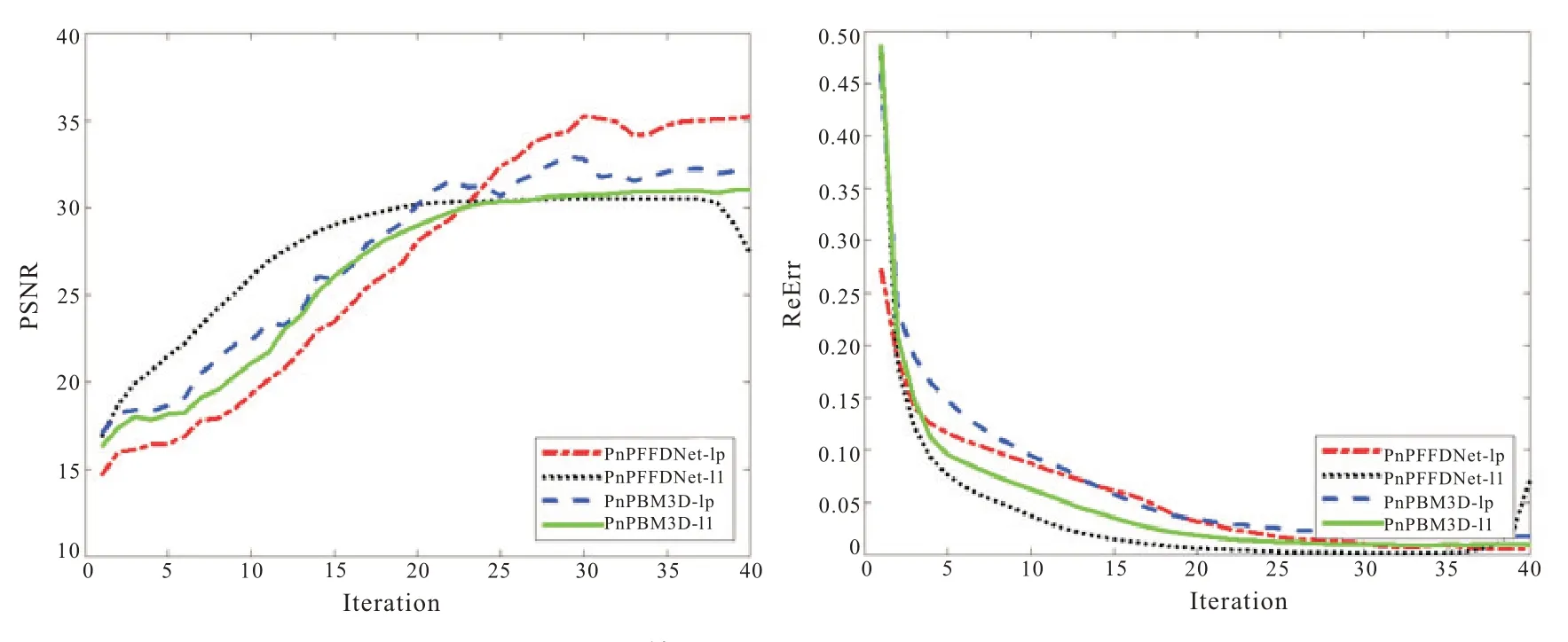
图2 四种算法的PSNR 与ReErr 曲线图
在数值实验中,灰度图“Boat”是被高斯核模糊,同时受到椒盐噪声或随机值噪声的污染,其中高斯模糊核的标准差为5,大小为7×7,脉冲噪声的水平分别为30%,40%与50%。表2 和表3 分别是椒盐噪声与随机值噪声下四种算法得到的复原图像的PSNR 值与SSIM 值。通过对比数值结果,与L1 模型相比,本文提出的基于Lp 保真项的模型获得更高的PSNR 值与SSIM 值。同时,因为BM3D 或FFDNet 去噪器的作用,图像复原的数值结果提升得非常明显。
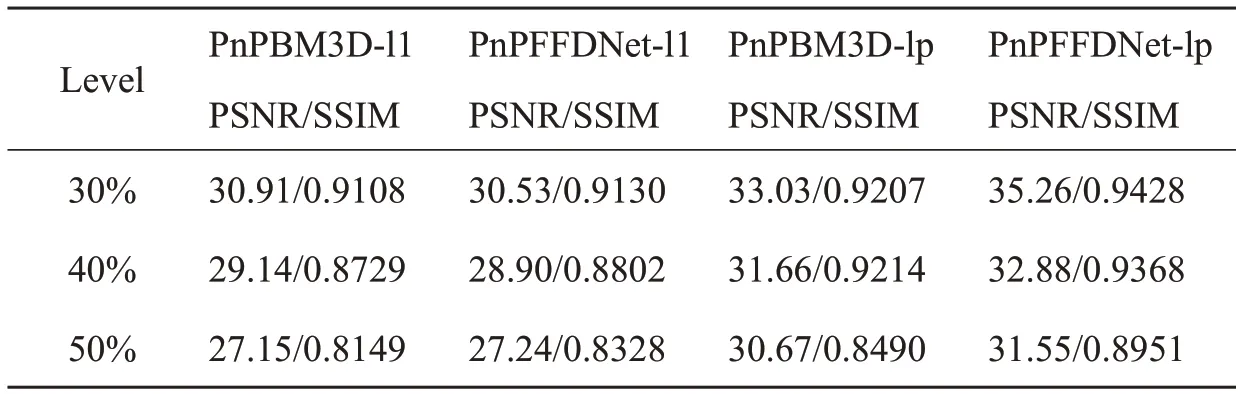
表2 标准差为5、大小为7×7 的高斯模糊核椒盐噪声下的复原结果
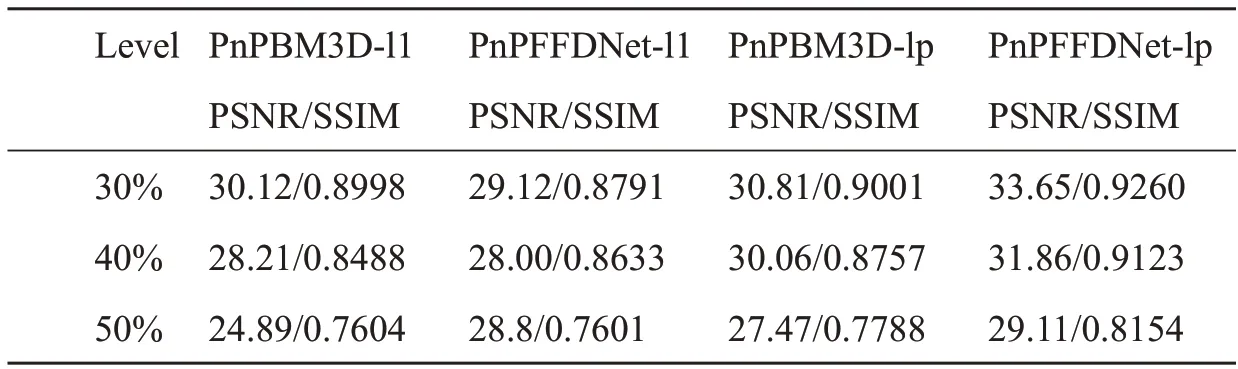
表3 标准差为5、大小为7×7 的高斯模糊核随机值噪声下的复原结果
为了更好地呈现复原图像的效果,图3 和图4给出了椒盐噪声与随机值噪声下的噪声图像与四种算法获得的复原图像。通过观察,我们发现基于Lp 保真项的算法在视觉效果上显得更清晰,能够尽可能多地保留图像的纹理和细节,同时很好地去除脉冲噪声。

图3 标准差为5、大小为7×7 的高斯模糊核椒盐噪声下的复原图像

图4 标准差为5、大小为7×7 的高斯模糊核随机值噪声下的复原图像
5 结束语
本文以基于学习的去噪器为正则项,提出了基于Lp 保真项的脉冲噪声模型。在数值计算上,结合即插即用框架,利用ADMM 算法将优化模型分解为三个子问题。针对子问题,依次应用FFDNet 算法、Lp 近端加速算法与快速傅里叶变换进行求解。经过数值实验对比,与其他脉冲噪声模型相比,所提出的模型获得的PSNR 与SSIM 值都有一定程度的提升。所提出模型得到的复原图像在视觉效果上更清晰,保留了图像中大量的细节和纹理,且去噪效果显著,有效提升了复原图像的质量。但是,由于即插即用(PnP)框架与Lp 保真项的非凸性,所提出算法在理论上的收敛性还无法保证,这也是我们进一步讨论和研究的问题。

