避障路径规划的算法研究

张喜英 崔智超 栾文璐 杨帅

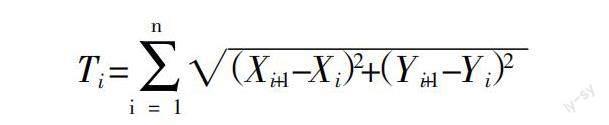
【摘  要】 将遗传算法应用于避障的路径规划，可根据遗传算法的流程，将路径长度设置为个体的适应度。首先将已知的工作环境进行建模，将障碍物与可行方格进行点化处理，并设置好起点与终点；随后设置好相应的变异率等参数；最后，输出适应度最高的路径作为最优路径。文章所应用的算法在MATLAB软件上进行仿真实验，实验结果表明，文章设计出的算法得到了最短的路径。该算法具有一定的可行性与实用价值。

【关键词】 遗传算法；避障路径规划；MATLAB仿真

一、遗传算法

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，它也是一种通过模拟自然进化过程搜索最优解的方法。

遗传算法主要包括编码、初始化种群、适应度函数建立、遗传操作等步骤。应用遗传算法来求解问题时，需要对子代基因进行反复的筛选、交叉和变异操作，最终得到符合条件的解或者迭代次数达到规定次数。遗传算法主要包括编码、初始化种群、适应度函数建立、遗传操作等步骤。

二、路径规划研究概述

（一）按照搜索范围划分

全局规划：通过对已知环境模型信息的处理，按照规划出的路径前进。全局规划得出最优解，取决于周围环境的参数。全局规划往往是适用于范围较小，环境复杂程度较低的空间，当环境模型较大时，全局规划的计算量会增大，运算的时间会变长。

局部规划：相比于全局规划对整个空间的解析，局部规划将所搜索的范围局限于当前位置的周围，使得在未知的环境中能够具有有效的避障能力。应用局部规划的实用性很高，与全局规划相比，当环境发生变化的时候不用再对运行环境进行建模，这大大提高了算法的实用性。然而局部规划可能会产生局部最优解，无法正常完成工作。

（二）按照工作环境划分

静态环境规划：静态环境是指工作的环境已知，不随时间的变化而变化。在这种环境中，障碍物是静止的，因而想要规划出一条最优路径较为简单。静态环境规划主要被应用于工厂等环境单一的地方。

动态环境规划：与静态环境相反，动态环境规划指的是在已知或者部分已知的环境中，存在有运动轨迹不明的障碍物，在这种情况下规划出一条最优的路径。

路径规划有如下特点：

1. 复杂性：当处于含有较多障碍物的环境或者处于动态环境中时，为了得到最优的路径，要进行大量的计算。尤其是动态环境中，规划的难度大幅提高。

2. 随机性：当工作环境相对复杂时，需要处理各种的突发状况以及不确定因素。

3. 约束性：按照规划好的路径前进时需要考虑到自身的大小、形状等物理因素，还要考虑自身移动速度的问题，这些条件是设计过程的重要部分。

4. 多目标性：路径规划的最优解具有多种评判标准，有的要求路径最短为优，有的要求到达时间最短，不可能完全达成所有目标，因此需要实时分析需求进而系统的权衡好各个要求。

三、避障路径规划方案算法的设计

将已知的工作环境进行建模，将障碍物与可行方格进行点化处理，并设置好起点与终点。具体过程如下：采用栅格建模的方法。其工作原理是将工作空间进行格式化处理，将工作的环境分割成大小相同的方格，空白部分表示可以行进的路径，黑色的部分表示障礙物，并设置好Begin（开始）和End（结束）两点，当两方格的中心能够相连时，表示为一条可行路径，否则不能相连。其障碍物环境的构建遵从矩阵。 随后设置好相应的变异率等参数，具体过程如下：

初始参数定义（染色体编码）：在路径规划方面，由起点到终点的可行路径即为遗传算法中的一条染色体。染色体中每一个基因片段对应可行路径片段，整个染色体可以看成是路径结点坐标集合。

适应度函数：通过种群中个体的特征来判断个体的适应程度。这里对适应度的定义即为路径的长度。通过输入一组节点坐标集合（个体），来得到所对应路径的总长度，其用公式表示为：

生成初始种群：种群即个体的集合，这里的种群即为可行路径的所有坐标集合。

计算个体的适应度：即将个体输入至适应度函数。这里是将坐标集合输入至适应度函数得出的路径长度。

预设条件：当达到种群繁殖次数的最大数值或者连续进化次数达到某一数值后最优的解不发生变化。终止条件设置为达到运算规定次数，且连续多次最短路径的结点集合不发生变化。

选择运算：用于筛检出计算至今符合条件的最优个体。这里表示将正在计算得出的路径同上一次计算的路径做比较，较短的一组路径坐标集将会被保留。

交叉运算：指当两条染色体达到配对条件以后，将各自的部分基因片段按照某种交叉方式来进行互换，得到两条新染色体的过程。在该算法中，交叉过程即为在具有一个或者多个相同坐标点的两条路径坐标集合中，随机将几个位于同一位置的坐标进行交换，形成新的两个坐标集合。

变异运算：染色体经过编码后将以编码串的形式表示，变异操作是将某段编码串上的基因编码数值随机替换为新的可用编码值，进而产生新的个体。这里将采用随机变异的方法，将某条路径集合中的坐标随机变化为其他的坐标，形成新的路径坐标集参与下次的运算。

根据遗传算法参数设定方法，种群中个体的数目para.popsize=50，交叉概率para.pcrossover=0.6，进化的最大代数设置为150代。在路径规划的过程中，运动轨迹T可以划分为一个个的线段，每一个有向线段的长度和即为所走路径的长度。线段由两点决定，以此为基础，运动路径可以看成是路径点的集合表示为：

T={（X1，X2），（X2，X2），...（Xn-1，Xn-1）}

在路径规划的数据存储过程中，路径点的存储采用坐标点的方式，根据坐标点Xi的数值来表示在当前环境中的位置。根据遗传算法原理经过编码所得的这条坐标集合路径称为已编码的染色体，在寻路计算的过程中，多条路径将会被记录并进行比较，进而得到最符合条件的一条。

种群可以看成是自然界生物种群的一种形式，一组字符串结构，可以被称为一个群体，通过随机选取的方式可以达成种群初始化的目的。在路径规划算法中，随机选取过程通过在除去起点与终点的空间内，随机选择坐标而表现，体现了种群的随机性。该算法由于存儲的方法为坐标点存储，因而算法中的种群可以看作为从出发点到目标点的所有可行路径的坐标集合。

文章使用初始化种群的方法：通过最优个体不断迭代的方法，以一群随机个体为单位，依照预置的评判标准选择出最优秀的个体，并放置到具有规模的种群中，重复该操作直到种群内个体达到饱和。具体步骤如下：

1. 首先设定好最大种群规模以及迭代次数等参数。

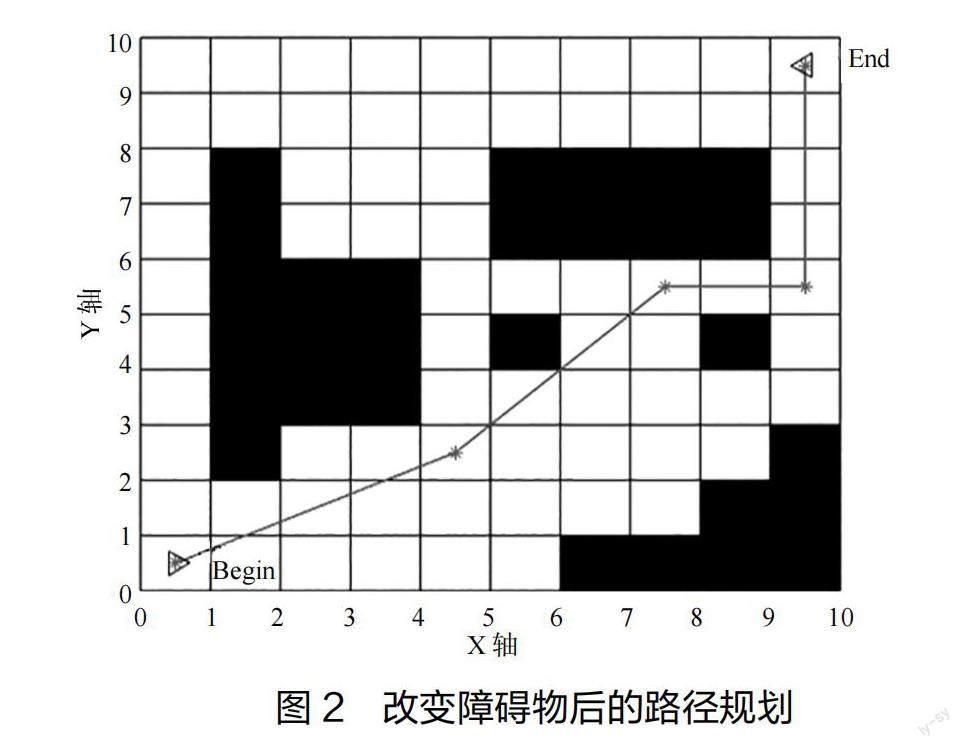
2. 由起点出发，以起点终点的位置方向为依据，随机选择下一个前进的位置，在栅格图上表示为与当前位置相邻的栅格。例如在图2中对应的坐标为（5，9），根据起始点的位置存在有向右（6，9）、向右上（6，10）、向上（5，10）三个方向，可以随机选择。

3. 进行随机选择的过程中，判断当前路径是否为有效路径的情况时，有如下两种情况：一为当前位置遇到了障碍物；二为在当前位置向四周进行移动时超出了边界。因此在算法中，两方格如果不能相连或者路径中存在有结点超出边界的情况则该路径为无效路径，随后重新进行随机选择。

在算法执行搜索的过程中，存在搜索点再次纳入搜索，造成循环路径的问题，为了减少算法的盲目性，将应用如下方法：在当前点附近随机选择一个点作为下次的路径结点，随后不停地重复该过程，在这个过程中所有经过路径的节点均被标记为数字1，其他为0，未被标注的节点才会纳入新路径节点的选择范围。一条路径选择完毕后，标记全部移除。

适应度是个体对环境适应性的评判标准，适应度需要用适应度函数来进行计算，在路径规划当中，适应度函数通过规划出的路径长度作为评价标准，以此标准来构建适应度函数。该算法中忽略了体积速度等物理因素，因而仅结合路径点的坐标数值这一个变量来对适应度函数来进行构建。

单条路径所包含的个体数为n，Xn，Yn分别表示路径节点的横纵坐标，L为该路径的总长度。

文章所使用的选择方法为二元锦标赛选择法，即从原种群中随机选择两个个体进行比较，选择最好的一个进入子代种群，随后重复该过程，直到种群达到原先规模或者达到最大迭代次数。这里具体表现为随机选择两条路径，将其长度数值L进行比较，较短的那一个进入子代种群。

原始种群中无可用个体选择结束。单点交叉法为文章的使用方法，单点交叉法即选出需要执行交叉操作的两个个体，然后随机选择交叉点，将两个个体在此点后的基因片段进行交换，交换后将形成两个新的个体。该算法表现为某两条可行路径结点集合内结点与结点之间的交叉互换，用数学思想表示为坐标与坐标的变换，在该算法的运行过程中，当选择好的两个个体满足了变异的概率p=0.04，则进入变异算子，这里采用的是基本位变异的方法，应用randperm函数随机选取一个基因位进行变异，变异的位置也同样适用randperm函数随机定位，最后，输出适应度最高的路径作为最优路径。整体遗传算法的核心思路就是对可行路径上的路径节点进行随机变异产生新的路径点，进而形成新的可行路径。遗传算法得出最优路径，通过节点之间的坐标平方相减再开方得出部分路径，最后部分路径相加来实现。

四、仿真结果与分析

为了证明设计的算法能够进行在存在有障碍物下进行路径规划，将采用MATLAB R2018a软件来进行对避障路径规划的模拟仿真。

设置好遗传算法的工作环境，起始地点坐标为（1，1），目的地坐标为（10，10）， 图1表示为一个10*10的矩阵，其横纵向的数字个数代表着工作空间中所有的有效结点，其中0表示可移动的区域，1代表障碍物的位置。该算法中Begin起点与end终点的位置分别设置为（0，0）与（10，10）。在障碍物环境下自动寻路的仿真结果与路径种群迭代图如图1、图2所示。

路径规划部分根据种群迭代次数可知，在改变障碍物前，种群随着迭代次数的增加，种群的目标值即运行的最短路径长度不断地减少，目标值曲线在14.94左右达到稳定值不再发生变化。根据结果数据可知在第一种障碍物环境下最短路径为14.9。同理在第二种环境下，曲线在14.7左右达到稳定，根据仿真出来的数据结果可知，最短路径为14.719。由仿真可知，当设置好起点与终点以后，所经过的路径长度是随着时间随机变化的，但最终会在某个数值达到稳定，这个数值就是最短的路径。

参考文献：

［1］ 孙波，姜平，周根荣，等. 改进遗传算法在移动机器人路径规划中的应用［J］. 计算机工程与应用，2019，55（17）：5-17.

［2］ 陈尔奎，吴梅花. 基于改进遗传算法和改进人工势场法的复杂环境下移动机器人路径规划［J］. 科学技术与工程，2018，18（33）：3-11.

［3］ Kai Yit，Parvathy Rajendran. Differential-evolution control parameter optimization for unmanned aerial vehicle path planning［J］. Systems，Man，and Cybernetics：IEEE Transactions on Systems，2019，43（06）：3-17.