基于板-梁理论的槽形截面薄壁杆件组合扭转能量方程与有限元验证

张文福,李沐阳,郭雪妞,邵琰皓,黄 斌,计 静,刘迎春

(1. 苏州科技大学土木工程学院, 江苏 苏州 215031;2. 安徽建筑大学土木工程学院, 安徽 合肥 230601;3. 南京工程学院建筑工程学院, 江苏 南京 211167;4. 东北石油大学土木建筑工程学院, 黑龙江 大庆 163318)

薄壁杆件以其优秀的材料力学性能及经济性能被广泛运用于航天、航海、建筑等领域.组合扭转问题是薄壁构件在工程中极为重要的理论问题.从力学本质上看,任何薄壁构件的扭转都属于组合扭转问题,即约束扭转和自由扭转并存.文献[1]研究了开口薄壁杆件约束扭转的经典理论;文献[2]借鉴传统薄壁杆件理论推导出直接边界元公式,并给出不同扭矩载荷和边界条件下的数值结果;文献[3]对冷弯薄壁开口截面钢梁的纯弯受力问题进行研究,在试验中解释了梁在受到纯弯作用情况下会绕着剪切中心扭转的现象,并给出了影响扭转弯矩的因素;文献[4]采用三种分析薄壁结构梁的有限元方程解释了面外翘曲现象,通过模拟薄壁结构梁模型在纯扭转和弯扭耦合作用下的响应,验证了提出的有限元表达式的准确性;文献[5]基于Vlasov理论建立一阶扭转理论来研究薄壁开口梁的约束扭转,并用半逆解法推导了圣维南自由扭转的表达式;文献[6]在传统开口薄壁杆件中考虑了剪切变形的影响,验证了修正剪切变形后数据的正确性;文献[7]提出一种把薄壁杆件截面进行拆分计算的理论方法,简化了截面畸变状态下的薄壁杆件力学模型,与基于壳单元的ANSYS软件模型分析结果吻合良好.

Vlasov薄壁构件理论是满足工程需要的一种近似工程理论.由于Vlasov引入扇性坐标的概念,因而仅适合分析单一材料薄壁构件约束扭转问题,并不适合弹塑性阶段的单一材料的结构构件屈曲分析,用于弹性阶段组合薄壁构件(如钢-混凝土组合梁)的屈曲分析会造成较大误差.

目前,在薄壁杆件理论研究领域,Euler梁理论和Kirchhoff板理论(简称板-梁理论)已取得众多理论研究成果[8-13].本文采用板-梁理论研究单轴对称槽形截面薄壁杆件组合扭转问题,并通过有限元模拟验证本文理论的正确性.

1 槽形截面梁的组合扭转理论研究

1.1 板-梁理论简介

板-梁理论的基本假设:

1) 平截面假设,即梁发生扭转变形时截面形状不变,据此可以确定板件形心的横向位移;

2) 变形分解假设,即每块板件的变形可以分解为平面内变形和平面外变形,对于开口构件,与此对应的纵向位移、应变能和初应力势能可分别按Euler梁力学模型和Kirchhoff板力学模型确定.

板-梁理论采用两套坐标系描述截面任意点的变形,这与Vlasov关于薄壁杆件问题的研究方法类似,整体坐标系与局部坐标系均符合右手法则,分别为oxyz轴、onsz轴.将整体坐标系的原点置于整体截面形心,局部坐标系的原点置于各板件的形心.槽钢截面坐标系设置与截面变形如图1所示.图1中:bf为翼缘宽度;tf为翼缘厚度;hw为腹板高度;tw为腹板厚度;E、G、μ分别为腹板与翼缘的弹性模量、剪切模量、泊松比;C、S分别为截面的形心、剪心,S在整体坐标系中的坐标为(0,y0);ay为上翼缘与剪心的距离;ef为上翼缘形心与截面形心的距离;ew为左右腹板形心与截面形心的投影距离;θ为梁发生扭转变形时截面产生的扭转角.

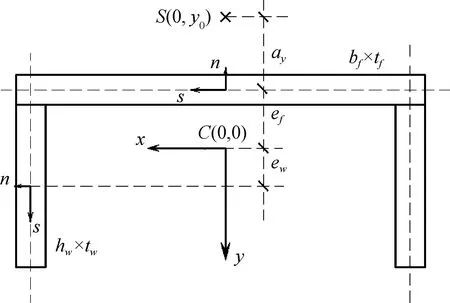
(a) 坐标系及符号

1.2 截面的形心与剪心

1) 形心的求解,根据合力矩为0的条件,图1中形心到上翼缘的距离为:

ef=Aw(hw+tf)/(Af+2Aw)

(1)

式(1)与材料力学的截面形心表达式一致.

2) 剪心的求解,上翼缘及左右腹板的形心不在一条线上,导致剪心位置存在偏移,当悬臂梁末端受到单位扭矩作用时,槽形截面的变形并非绕着自身形心扭转,其扭转中心距板件形心有一定偏移,传统理论扭转刚度推导中令剪心S(0,y0)与临近板件中线距离为ay,由图1可见,y0=-ef-ay,对截面剪心的求解即是对未知数ay的求解.

1.3 槽形截面的能量变分模型

1.3.1 板件截面任意点的位移

在求解变形应变能时可将三块板单独进行分析求解.以上翼缘为例,在整体坐标系下,其形心坐标为(0,-ef),上翼缘板件任意点坐标为(s,-ef-n),上翼缘变形产生的位移可表示为:

α=2π,x-x0=s,y-y0=ay-n

(2)

(3)

式中,rs、rn为板件剪心到s、n轴的距离;

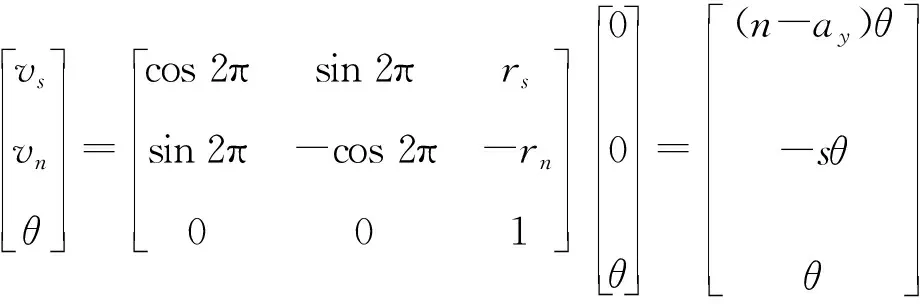
(4)

式中,vs、vn为板件任意点沿s、n轴的距离.

上翼缘形心的横向位移(沿上翼缘n、s轴)和纵向位移(沿梁纵向z轴)为:

(5)

根据变形分解原理,可将变形分解为面内变形与面外变形:

(6)

1.3.2 板件面内扭转产生的应变能

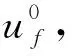
(7)

上翼缘板沿局部坐标宽度方向s轴的位移为:

vf=-ayθ

(8)

纵向位移按整体坐标z轴考虑,需要根据Euler梁力学模型确定:

(9)

采用相同方法对槽形截面另外两块板件进行分析.Vlasov在传统理论中求解主扇形极点和主扇形零点时采用N=Mx=My=0这一条件,即开口截面薄壁杆件仅受有扭转作用荷载时满足条件:在其任何横截面上只产生扭矩,不产生轴向力,且对截面整体坐标系两轴也不产生弯矩.其中轴向力和弯矩的表达式为:

(10)

在板-梁理论求解槽形截面的组合扭转问题时,采用类似的方法,以轴向力的求解为例,三块板的轴向力之和为:

(11)

由式(10)的方程组可求出三块板件局部坐标n轴方向的侧移未知数解.把所得结果代入式(7)中,可求出其应变表达及面内弯曲应变能.以上翼缘为例,其面内弯曲应变能表达式为:

(12)

1.3.3 剪心的求解

三块板件的相交处在理论上是耦合的,以右上角为例,有:

(13)

式中,sf、sw分别为板件在局部坐标s轴方向的位置.

右上角的位移变形协调,即上翼缘的右端与右腹板的上端应变相等,由式(13)可推导出板-梁理论的槽形截面剪心表达式:

(14)

传统理论推导出的槽形截面剪心表达式为:

(15)

表1 板-梁理论ay与传统理论剪心计算结果

1.3.4 板件面外应变能的求解

依据变形分解原理,以上翼缘为例,对板件的变形位移进行分解.沿局部坐标厚度方向s轴的位移为:

uf(s,z)=-sθ

(16)

沿局部坐标宽度方向n轴的位移为:

vf(n,z)=nθ

(17)

纵向位移(沿z轴的位移)依据Kirchhoff薄板模型来确定,即:

(18)

由板-梁理论得到上翼缘面外应变能为:

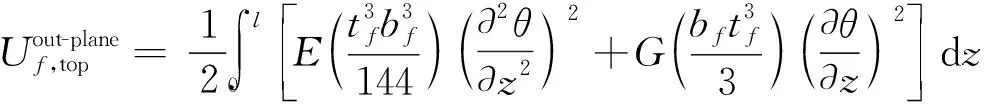
(19)

运用类似方法,可求出左、右腹板应变能表达式.

1.3.5 总应变能

槽形截面梁的总应变能简化为单变量的组合扭转表达式为:

(20)

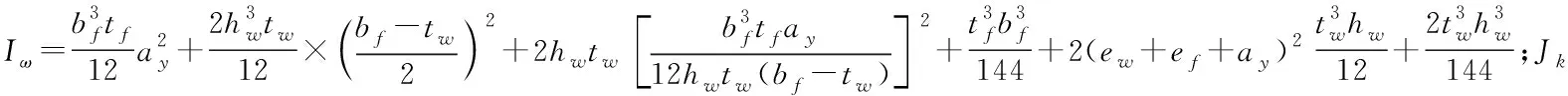
用传统理论推导出的槽形截面自由扭转惯性矩、约束扭转惯性矩表达式为:

(21)

式中:h为截面的高;b为截面的宽;t为板件的厚度;d为当选择剪心为扇形极点时,左、右腹板在传统理论扇性坐标中位移为0处的点到上翼缘中面的距离.

表2为板-梁理论与传统理论截面常数计算结果.由表2可见,4组截面参数两种理论计算得出:自由扭转惯性矩相等;约束扭转惯性矩的对比误差较小,且当截面尺寸越接近薄壁杆件时,其误差越接近于0.

表2 板-梁理论与传统理论截面常数计算结果

1.3.6 总势能方程

在z=L处作用一集中扭矩,则钢梁的总势能为:

Π=U+V=U=

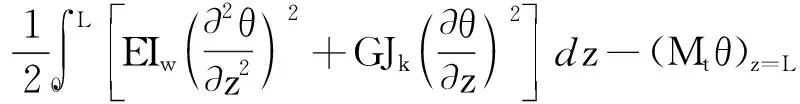
(22)

平衡微分方程为:

EIwθ(4)-GJkθ″=0

(23)

对于悬臂梁的边界条件,方程解为:

(24)

令z=L可得出端部转角的表达式为:

(25)

2 槽形截面梁的组合扭转有限元验证

2.1 槽形钢悬臂梁组合扭转的有限元验证

为确保有限元模拟的正确性,以文献[7]中的案例建立有限元模型.图2所示为两端固定的槽钢,弹性模量为210 kN/mm2,泊松比为0.25,集中荷载1 kN作用于跨中形心正上方,在有限元软件ANSYS中运用SHELL181进行模拟,剪心处扭转角最终计算结果为3.667×10-4rad.

图2 两端固定槽钢的受力情况(mm)

运用本文建立的ANSYS模型,施加文献[7]中的边界条件及荷载,由图3可见,剪心处扭转角的最终计算结果为3.66×10-4rad,和文献[7]结果一致,验证了本文建立有限元模型的正确性.

图3 ANSYS模型施加文献[7]边界条件及荷载的计算结果

在此基础上,选取多组槽形截面梁尺寸进行有限元建模,材料为钢材,弹性模量为2.06×1011N/m2,泊松比为0.3.在有限元建模时,为模拟出悬臂梁边界条件,约束悬臂梁的固定端6个自由度,自由端施加1 kN的单位扭矩,同时在施加端部扭矩的截面设置接触单元CONTA175和TARGE170以保证模型受力变化的均匀,采取CERIG命令模拟刚周边的假定,在同一截面中选取一点作为主节点以保证截面的整体扭转,端部约束及荷载施加如图4所示、截面刚性区域定义如图5所示;整体变形和L/2处截面变形模拟结果如图6、图7所示.

图4 端部约束及荷载施加

图5 截面刚性区域定义

图6 整体变形图

图7 L/2处截面变形图

2.2 槽形钢悬臂梁组合扭转有限元模型收敛性分析

通过网格划分精细化检查有限元模型的收敛性,结果如表3所示.由表3可见,随着网格划分的密度增加,转角θ′逐渐收敛,证明了该模型的模拟结果具有参考价值.

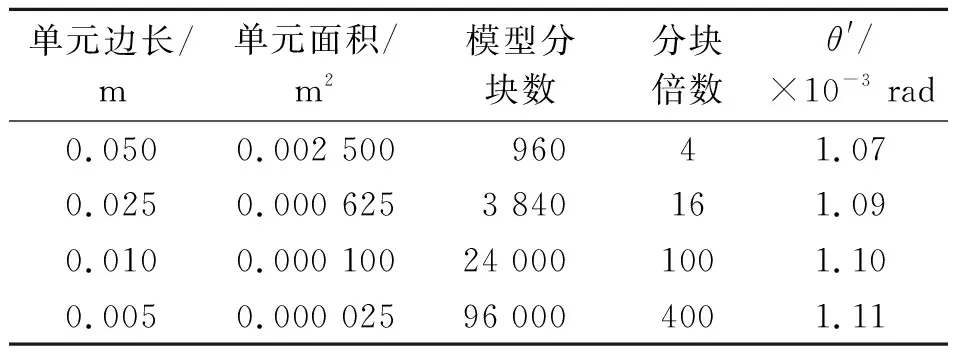
表3 有限元网格细化对结果的影响

2.3 理论计算与有限元模拟结果对比

采用不同的算例进行理论计算和有限元模拟,结果如表4所示.由表4可见,对于等厚度的槽形截面梁,当高跨比为6时,理论计算θ与有限模拟θ′结果误差为-4.85%,当槽形梁的高跨比变大时,θ与θ′误差减小;对于翼缘与腹板非等厚的槽形截面梁,当高跨比为6时,θ与θ′误差为-4.41%,与等厚截面梁类似,其θ与θ′误差随高跨比增大而逐渐减小.

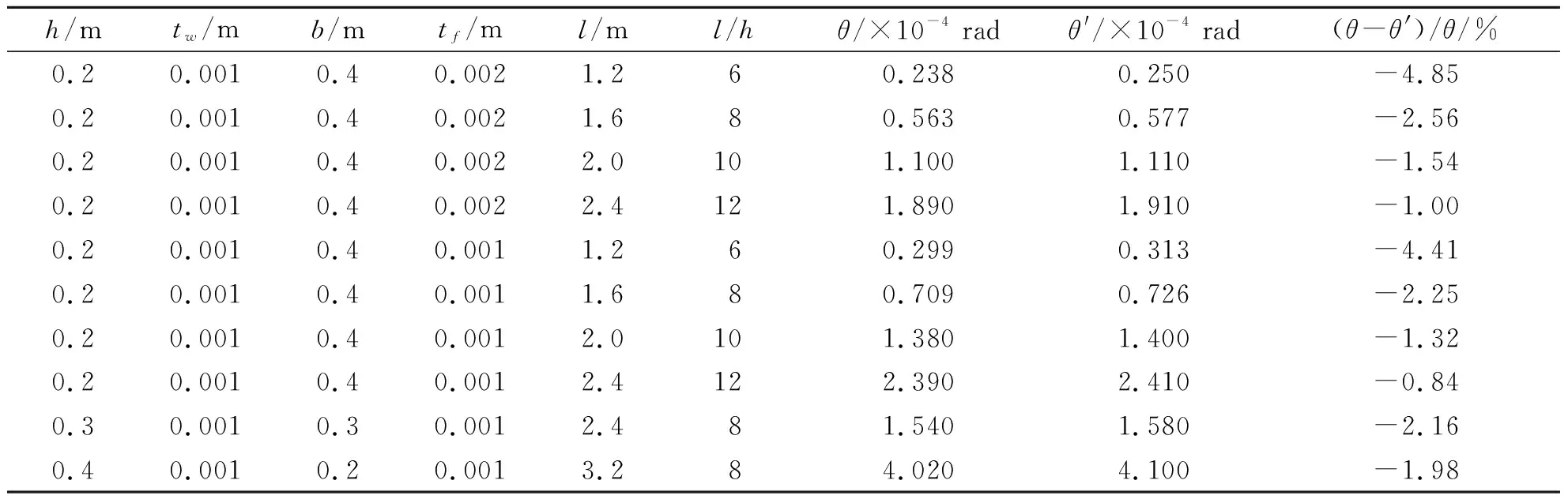
表4 槽型截面悬臂梁扭理论计算θ和有限元模拟θ′结果

本文选取两组不常见的截面,通过理论计算与有限模拟对比,发现其误差保持在较小的合理范围内.通过多组数据的对比,验证了本文方法在进行槽型截面相关问题研究时具有较广泛的适用范围,结果具有一定的正确性.

3 结论

1) 本文基于板-梁理论推导得出槽形截面薄壁杆件悬臂钢梁的组合扭转总势能表达式及槽形截面的约束扭转刚度、自由扭转刚度表达式,基于能量变分模型以及微分方程模型得出槽形悬臂钢梁的扭转角表达式;

2) 利用ANSYS有限元分析软件的SHELL181单元建立有限元模型,在保证模型正确性的前提下,经过对比可知,该单元适用于薄壁构件的相关理论模拟分析,与理论计算对比可知,在悬臂梁的自由端施加接触单元可以有效提高有限元的模拟计算精度,且其后处理结果不会发生畸变变形.

3) 推导出槽形截面的形心表达式、剪心表达式,其中形心表达式采用合力矩为0的条件求解,剪心表达式根据三块板件的轴力以及弯矩为0的条件求解,通过多组截面尺寸的对比得出,形心的理论计算与有限元的截面特性完全相同,而剪心表达式与传统理论得出的表达式形式上一致,剪心的误差最大绝对值为2.81%,证明了本文采用的形心、剪心求解方法的正确性,在求解类似的截面形心、剪心时,具有理论参考价值.