隧道盾构施工地表沉降量预测方法研究

张延彬

(中铁十八局集团有限公司, 重庆 401135)

城市快速发展使得土地资源价值的大幅度提升,城市可用面积越来越少,地下空间的开发逐步引起人们的重视.隧道是地下空间利用最主要的一种方式.但由于各地区土地具有一定差异性,地下隧道在施工过程中还会存在一定的问题[1],如周边建筑物施工方法的不同以及土层地质环境的差异都会导致地表出现沉降现象.地表沉降会导致一系列的安全性问题,若是沉降量过大还会造成周边建筑物的损坏.为了确保隧道的盾构施工不会对周边环境造成过大损害,需要对沉降量进行预测研究.文献[2]通过多种不同的沉降指标,对地表沉降预测进行了综合分析,同时结合遗传算法对BP神经网络进行优化,以此搭建相关的预测模型,该模型可以提高地表沉降量的预测精度,具有较好的拟合性能和收敛效果;文献[3]在小波变换的基础上对地表沉降预测模型进行优化,解决了预测过程不稳定的问题,同时将不同的参数分量叠加处理,经过回溯重构后,大幅度降低了预测误差;文献[4]通过估计地表沉降影响范围,设计一种DE-SVR算法下的预测模型,通过差分进化算法对地表沉降的影响因素进行综合分析,利用该模型得到了更高、更稳定的预测结果.

为进一步提高预测精度,本文设计一种新的隧道盾构施工地表沉降量预测方法.

1 隧道盾构施工地表沉降计算

在隧道的盾构施工过程中,地层会出现一定的损失,这直接导致地表的大幅度沉降.因此,在几乎所有的隧道盾构施工路线上,地表都会呈现出凹型,表现为外围较高、内部较低[5-6].为提高隧道地表沉降的计算精度,本文从横向沉降与纵向沉降出发,设计一种综合的沉降预测模型.

1.1 横向沉降

隧道横向沉降是指隧道侧向发生的沉降现象.隧道横向沉降会导致地面和建筑物的不均匀沉降,进而引起结构破坏、地面下沉、管线断裂等问题.横向沉降的主要表现形式如图1所示.

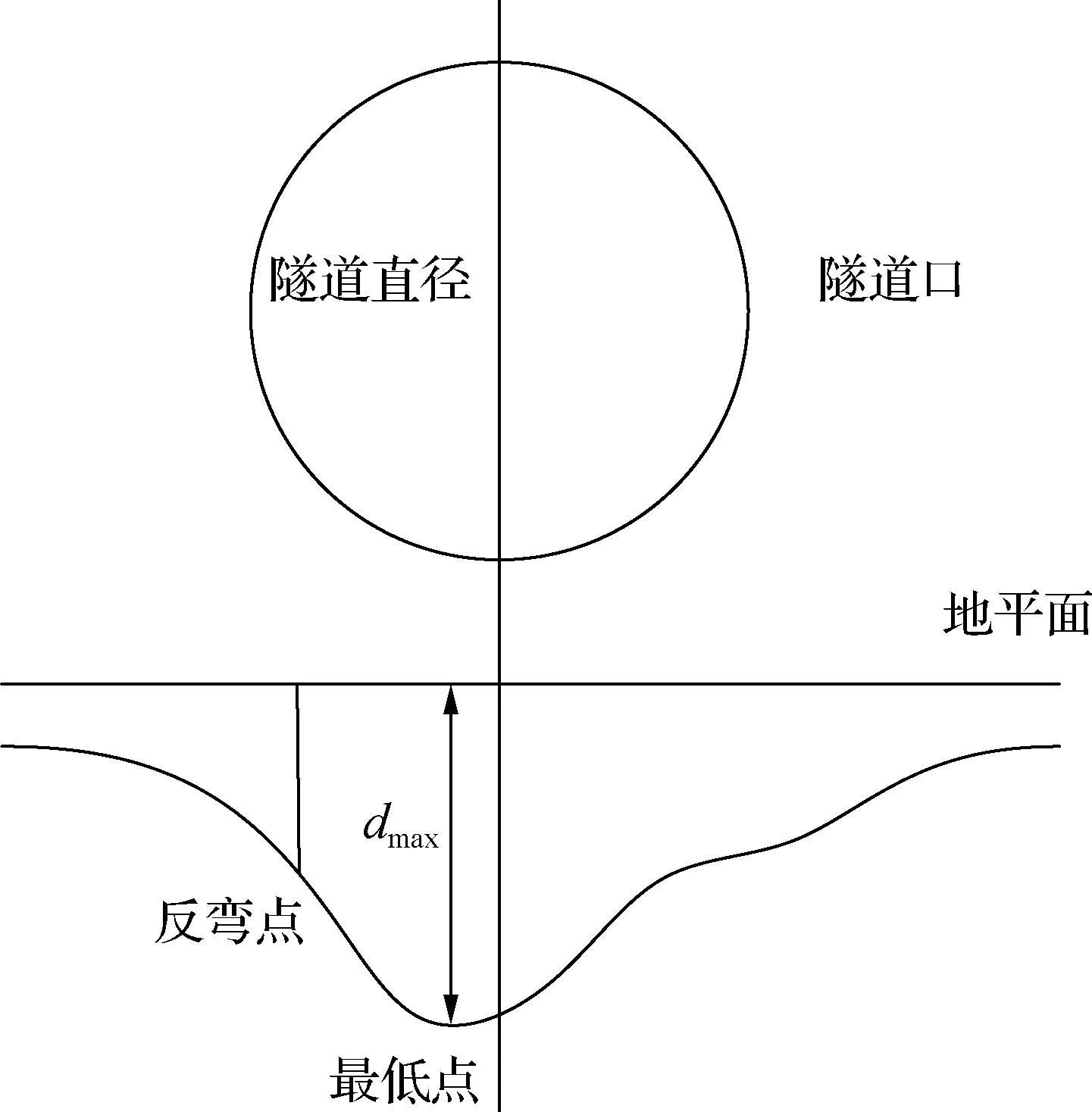
图1 隧道横向沉降示意图

图1中,反弯点和最低点都是描述隧道横向沉降变化的关键点.反弯点是指隧道纵断面中纵向曲率最大的点,也可称为最大下沉点.最低点是指隧道纵断面中沉降最深的点,也可称为最大沉降点.通过监测和分析隧道纵断面上的反弯点和最低点的变化情况,可以了解隧道横向沉降的分布特征、程度和趋势,从而采取相应的修复或补救措施,这对于预测隧道盾构施工地表沉降量、评估隧道结构的稳定性、影响沉降范围和地表破坏等方面具有重要意义.地表沉降槽内的平均沉降量计算公式为:

d(x)=dmaxexp(-dxy2/(2pi2))

(1)

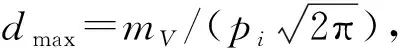
1.2 纵向沉降

隧道盾构施工会带动地层的变化,进而在周边的建筑物上生成应力附加值,其沉降趋势如图2所示.

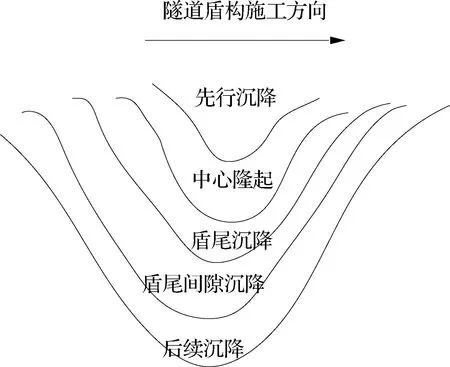
图2 隧道纵向沉降示意图

在纵向沉降中,分为先行沉降、中心隆起、盾尾沉降、盾尾间隙沉降以及后续沉降五个步骤[10-11].其随时间的变化可以形成一个双曲线,其函数表示形式为:

(2)

式中:h(t)为隧道沉降趋势在时间作用下的变化函数;Ti为沉降速率;Tf为沉降持续时间;a为回归参数,与该区域的地层性质有关;b为隧道参数[12-13].

2 设计沉降预测模型

通过隧道盾构施工过程中地表的沉降总量计算方法对沉降值进行预测,沉降预测模型设计流程如图3所示.

图3 沉降预测模型设计流程图

由图3可见,在区分模型的非线性关系前,需要对数据进行预处理,并设置相应的影响系数,数据经过归一化处理后,可以直接对其进行降维分析[14].隧道盾构施工样本的矩阵形式为:

(3)

式中,Hij为第i个施工参数下的第j个地质变量.

式(3)的协方差矩阵为:

(4)

由式(4)可以建立属性样本集.将样本集分为测试集与训练集,并建立相应的沉降预测模型.将测试集输入训练好的模型中,采用损失函数评价模型是否满足标准:

(5)

式中:G(k,g(x))为函数k与函数g(x)之间的损失函数;k、g(x)分别为地表沉降的实际数据以及地表沉降的预测值[15].

根据该模型,可以得到隧道盾构施工下地表沉降量预测结果.

3 试验研究

为测试本文设计的隧道盾构施工地表沉降量预测方法的有效性与准确性,首先将某隧道的其中一个路段作为试验对象,筛选沉降数据并进行统计,得到数据的预处理结果;然后建立训练集与测试集,对样本数据进行拟合分析,并计算其相对误差与均方误差,以此判断本文预测方法的优越性.本试验所有的数据处理环节均在Matlab软件上进行.

3.1 数据选取与预处理

隧道盾构施工地表沉降量的预测指标共有5个盾构掘进参数,分别为千斤顶总推力、千斤顶刀盘扭矩、平均土压力、贯入度、注浆量,其地质参数分别为断面地下水位、隧道洞身围岩黏聚力、内摩擦角、侧压力系数、覆土厚度等,这些影响参数均来自于该段工程施工方的地质勘查报告以及监测日报表.在沉降量的监测日报表中,经常会出现错漏数据,为保证沉降预测模型的准确性,需要对其进行人工筛选.经过预处理后,得到训练组数据和预测组数据.由于不同数据之间的量纲不同,需要对其进行归一化处理,将所有初始数据统一表示为(0,1)区间的数据,映射结果为:

f(k)=(ki-kmin)/(kmax-kmin)

(6)

式中:f(k)为初始数据进行归一化处理后的映射结果;ki为初始地表沉降数据;kmin、kmax分别为该维度下地表沉降数据的最小值、最大值.

由式(6)计算得到归一化处理后的数据如图4所示.由图4可见,经过归一化处理后的地表沉降数据均在0～1,基本消除了数据之间量纲不同带来的影响.

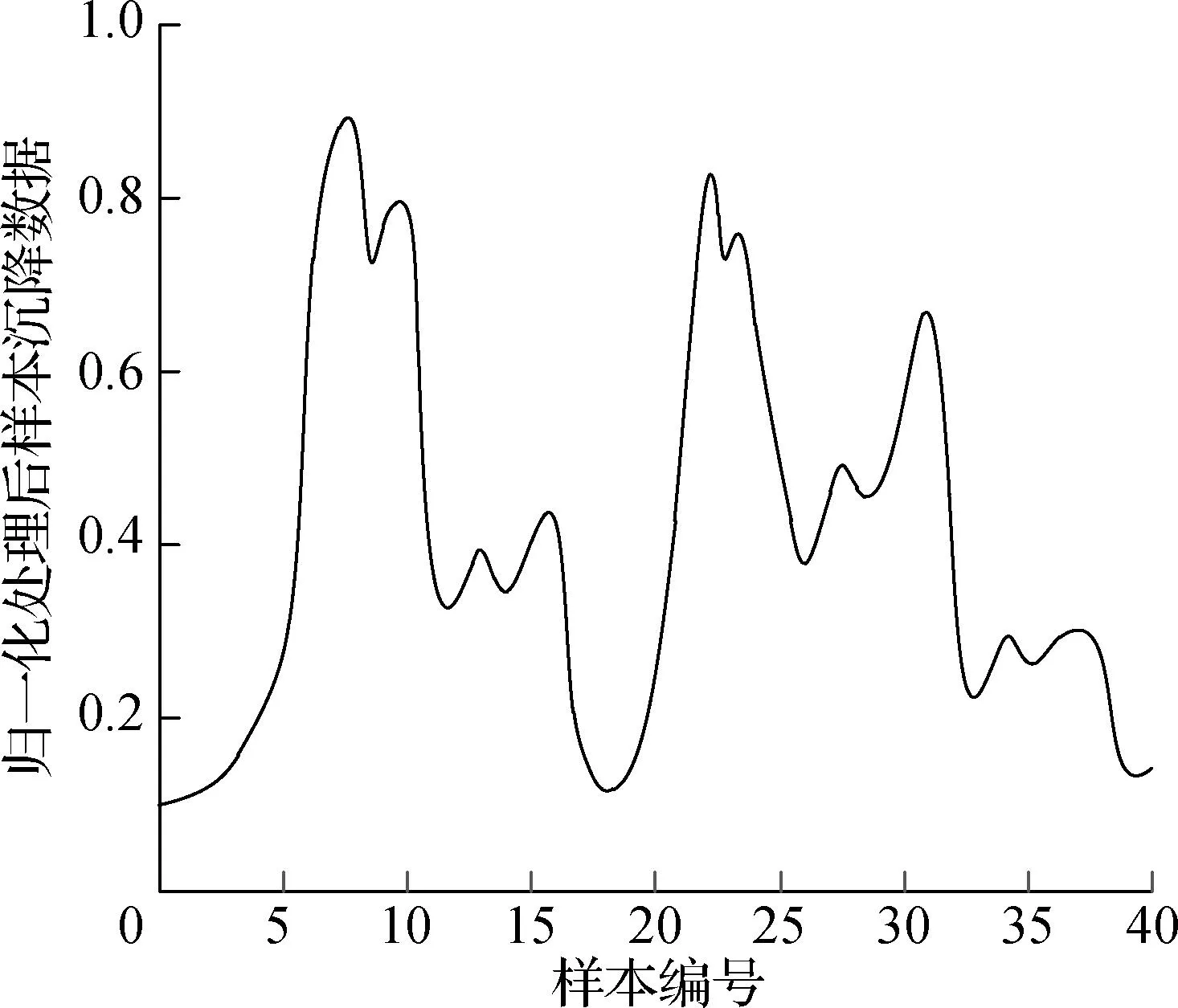
图4 归一化处理数据

3.2 模型预测值计算

在隧道的盾构施工过程中,土体大多不具备线性特征,因此,在本试验中将高斯核函数作为模型函数,将5个盾构掘进参数及5个地质参数分别建模,然后将二者组合,建立综合参数条件的预测模型.将盾构掘进参数建立的模型作为模型1,将地质参数建立的模型作为模型2,将综合参数条件下的预测模型作为模型3.在核函数内,如果一个定义域内不存在连续的点,则可以依据隐含层的神经网络完成对于序列样本的预测.设置模型的输入值、输出值,并建立隐含层作为模型复杂度的评判依据.利用隐含层的节点,对输入层与输出层的神经元进行判别,隐含层的神经元数量计算公式为:

(7)

式中:pn为3个模型中隐含层的神经元数量;xi、yi分别为预测模型中输入层、输出层的神经元数量;dm为神经元节点参数,一般取1～10的整数.

对隐含层内的节点数量进行反复训练,以训练样本为最大收敛值.当样本量不断增加时,可以以此搭建相应的网络模型.此时实际沉降值、模型1预测值、模型2预测值以及模型3预测值在40个样本编号下的地表沉降量如图5所示.

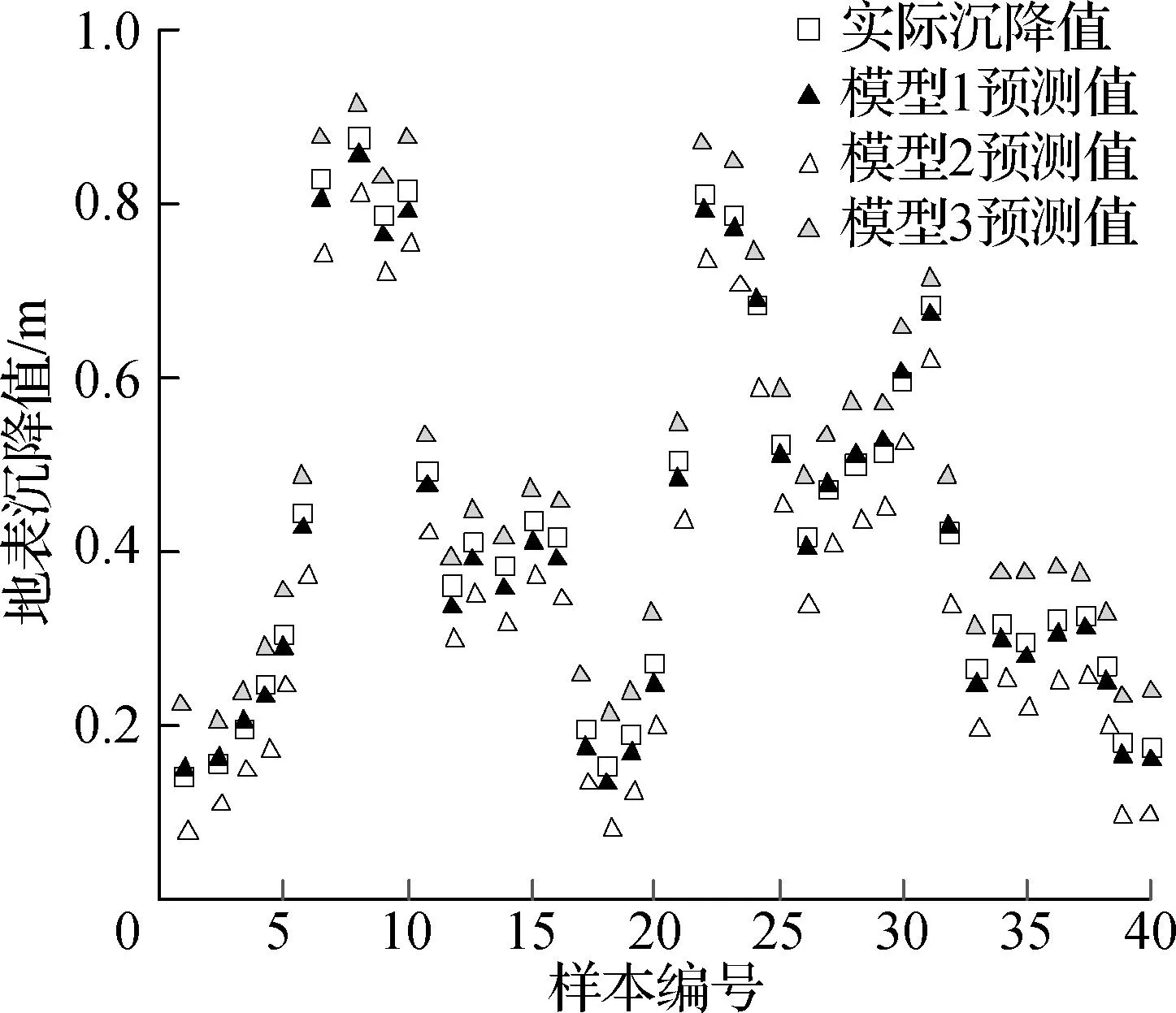
图5 不同参数条件下训练点沉降数据预测值

将图5与实际的沉降值进行对比可知,模型1的预测值低于实际沉降值,模型2的预测值高于实际沉降值,综合二者特点建立的模型3的预测值与实际沉降值最接近.由此可知,综合盾构掘进参数以及地质参数的预测值最准确.

3.3 沉降量预测值误差对比

在计算沉降量预测值与实际沉降值的误差时,为保证结果具备代表性,将决定系数、均方根误差、平均绝对误差作为本次试验中的三种评价参数,计算公式为:

(8)

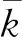
利用式(8)分别计算以上40个样本点的预测值误差,得到本文模型、GA-BP神经网络模型、EWT-Prophet模型、DE-SVR模型的预测结果.对四种地表沉降量预测方法的决定系数、均方根误差以及平均绝对误差进行计算,具体预测结果如图6所示.

(a) 决定系数

决定系数一般为0～1的小数,该参数越接近1.0,证明该方法的预测精度越高.由图6(a)可见,本文方法的决定系数在0.8～1.0,GA-BP神经网络算法的决定系数在0.7～0.8,EWT-Prophet方法的决定系数为0.7～0.9,DE-SVR模型的决定系数为0.6～0.7.同一个样本下,本文方法的决定系数均高于其他方法.

均方根误差与平均绝对误差越小,证明模型预测精度越高.由图6(b)和图6(c)可见,本文方法的均方根误差和平均绝对误差分别在0.05～0.15 mm和0.05～0.07 mm,GA-BP神经网络算法的均方根误差和平均绝对误差分别在0.05～0.20 mm和0.08～0.17 mm,EWT-Prophet方法均方根误差和平均绝对误差在0.13～0.23 mm和0.08～0.20 mm,DE-SVR模型的均方根误差和平均绝对误差分别在0.10～0.35 mm和0.15～0.25 mm,误差最大.由此可见,本文方法的平均绝对误差均小于其他三种方法,均方根误差基本上小于其他方法.通过上述数据可知,本文的隧道盾构施工地表沉降量预测精度高于三种传统方法,可以应用于相关预测领域.

4 结语

结合横向沉降及纵向沉降规律,本文设计一种新的隧道盾构施工沉降量预测方法,通过决定系数、均方根误差以及平均绝对误差的测试可知,本文方法可以更准确地对隧道周边区域地表的沉降量进行预测,更好地保证施工人员的安全,同时减少施工灾害的发生.