具有自适应多子群的海洋捕食者算法新策略
谢家烨
(南京工程学院工业中心/创新创业学院, 江苏 南京 211167)
现代电子信息技术领域中许多实际问题需要求解最优值,包括峰值检测、自适应滤波、电路参数选择、电路布局优化、PID控制器参数整定和控制策略优化等.这些问题复杂,智能优化算法在其中发挥着重要作用[1-2].智能优化算法的核心思想是模拟大自然的进化过程,通过对一定规模的种群进行分组搜索,以实现全局最优解的探索和局部最优解的更新,从而应用于解决实际问题[3-6].
在众多智能优化算法中,海洋捕食者算法(marine predators algorithm,MPA)是一种基于自然界捕食者与猎物关系的优化算法[7].该算法源于生物演化过程和进化计算理论,主要通过对种群进行分组搜索来实现全局最优解的探索,避免局部最优解的困扰,具备较强的自适应性和鲁棒性.MPA模拟了海洋生态系统中的捕食者-猎物关系,提高了寻优效果和成功率.
近年来,MPA在计算提取光伏参数的最佳值[8]、新冠病例数预测[9]、无线传感器网络定位问题[10]等方面得到应用.然而,传统的MPA存在全局最优解质量对初始种群质量敏感、难以有效监控种群状态以及迭代后期容易被竞争到其他种群导致无法获得全局最优解等不足之处.
为了克服MPA的不足,许多学者提出了多种改进方法.文献[11]通过使用量子理论搜索机制对MPA进行修正和加强,提高了算法在多级图像分割问题中的探索和开发能力;文献[12]引入多子群海洋捕食者算法(multi-subpopulation marine predators algorithm,MSMPA),将整个种群划分为3个子群,并针对不同子群采用不同的优化策略,改善了算法的寻优效果;文献[13]和文献[14]将粒子群算法和飞蛾火焰算法与MPA相结合,避免了陷入局部最优解的困扰.这些改进提高了MPA的效率和性能,同时也增强了算法在各种非线性问题中的优化表现,提高了处理复杂实际问题的实用性和能力[15-17].
本文以MPA为基础,对算法中的探索和开发阶段系数进行优化.与MSMPA类似,种群在每次迭代后根据个体适应度值分为领导者子群、追随者子群和衔尾者子群,本文优化追随者子群的更新算法,并根据不同阶段自适应调整3个子群的种群规模,使算法能够更好地平衡探索和开发过程,在解决优化问题时表现出更高的效率和性能,进一步提高了算法的求解最优值的精度和全局寻优能力.通过数值试验表明,本文算法在多个测试函数上的表现明显优于MPA及其他同类优化算法,充分证明了本文算法可以有效解决优化问题.
1 海洋捕食者算法及其多子群策略
1.1 海洋捕食者算法
2020年,文献[7]提出了一种基于种群进化的MPA.与其他进化算法相比,该算法具有结构简单、易于实现的特点.MPA不需要复杂的数学模型或繁琐的参数调整,方便使用和改进,能够有效解决各种实际问题.MPA的求解步骤为:
1) 初始化种群,计算公式为:
pij=pmin+rand·(pmax-pmin)
(1)
式中:pmax、pmin分别为求解区域的上、下边界;rand为[0,1]之间服从均匀分布的随机数.
以pij为元素构成猎物矩阵(prey matrix):
(2)
式中:n为种群规模;d为种群中个体的维度.
计算矩阵(2)的每行向量Pi=(pi1,pi2,…,pid)的适应度,其中适应度最优的个体PM复制n份构成精英矩阵(elite matrix):
(3)
猎物矩阵和精英矩阵的维度相同.
2) 考虑猎物与捕食者速度比不同的情况,模拟捕食者和猎物的整个生命过程,MPA优化过程分为三个主要阶段:
① 探索阶段,此阶段迭代次数it小于最大迭代次数Max_it的1/3,采用运动模型:
(4)
式中:si为游走步长;Ei、Pi分别为E、P的第i个元素;RB为随机向量;p为常数,p=0.5;R为[0,1]的随机向量;为逐项乘法.
② 转换阶段,此阶段迭代次数范围处于最大迭代次数的1/3~2/3,算法中前一半种群采用Lévy游走进行开发,后一半种群采用Brownian游走进行开发,计算公式为:
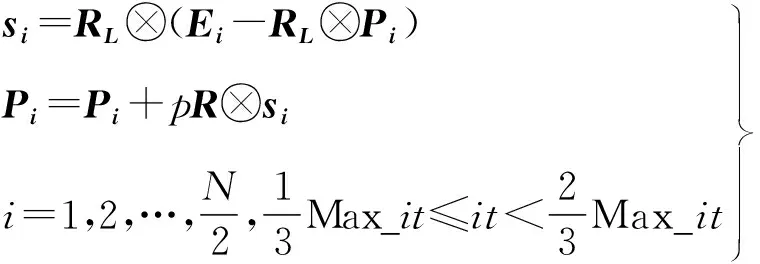
(5)
式中,RL为基于Lévy游走的随机向量.
(6)

③ 开发阶段,此阶段迭代次数大于最大迭代次数的2/3,计算公式为:
(7)
3) 涡流形成和鱼类聚集装置,为了跳出局部解,进行更新计算:
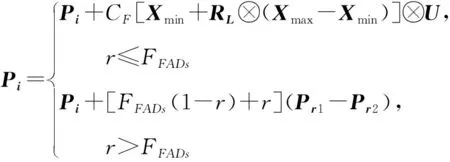
(8)
式中:FFADs取值为0.2;U为一个二进制向量;Pr1、Pr2分别为任意选取的2个猎物;r为任意随机数,r∈[0,1].
1.2 多子群海洋捕食者算法
文献[12]提出一种多子群自适应策略海洋捕食者算法,旨在解决传统MPA全局搜索能力不足和易陷入局部最优解的问题.该算法通过对捕食者个体适应度值排序,将捕食者平均分成领导者、追随者和衔尾者3个子群.适应度值排名在前1/3的个体属于领导者子群,排名在1/3~2/3的个体属于追随者子群,排名在后1/3的个体属于衔尾者子群.
在多子群海洋捕食者算法中,领导者子群位置固定,追随者子群更新公式为:
(9)
衔尾者子群更新公式为:
Pi=Pbest-Pmean-r3(lbi+r4(ubi-lbi)),
(10)
式中:Pbest表示全局最优个体;Pmean为所有个体位置矢量的平均值,且基于动态边界;lbi、ubi分别为该个体位置向量的动态下限和上限;r3、r4为服从[0,1]均匀分布的随机值.
2 多子群海洋捕食者算法的新策略
MSMPA通过增加种群多样性、减少局部最优解的影响提高了算法的收敛速度和精度.然而,MSMPA在求解某些特定模型时仍存在一定精度和速度方面的缺陷.为此,本文对MSMPA进行改进.
2.1 优化控制参数
通过模拟自然界中捕食者和猎物的实际行为,在策略中更新参数CF′和引入控制参数w来调整捕食者朝向猎物的步长,以平衡算法的探索和开发阶段,从而增强MPA探索和开发能力.通过更新和改变参数,可以提高MPA的效率和有效性.
本文采用新的自适应参数来控制捕食者的移动步长,参数计算公式为:
(11)
以非线性参数w作为控制参数,计算公式为:
(12)
引入新的线性参数CF′的目的是在算法第二阶段的开发阶段和整个优化过程中保持高探索能力,从而增加算法达到全局最优解的机会,避免被困在局部最优解中;w′值非线性减小,使得在探索和开发阶段达到平衡,则式(5)至式(8)更新为:
(13)
(14)
(15)
(16)
2.2 交替使用参数
本文引入的系数可以在大多数标准函数的求解中加速收敛和提高精度,但对于部分标准函数的求解,这一改变也可能带来不稳定性.
为了消除不稳定性,本文提出在迭代过程中不是每次都使用新引入的系数,在部分迭代中仍然保持传统算法的系数,这样可以弥补新系数带来的不稳定性,同时确保新算法的有效性.具体的做法为:引入一个参数M,若迭代次数可以整除M,采用传统MPA的参数进行计算;若迭代次数无法整除M,采用新的参数.这样做的好处是能够根据具体情况动态地调整算法参数,进一步提高算法性能.试验表明,引入参数M=5可以在很大程度上提高算法的收敛速度,同时平衡算法的精度和稳定性.
2.3 优化追随者子群
在每次迭代后,采用类似MSMPA的修正策略,即根据适应度值分为3个子群,其中,领导者子群和衔尾者子群的处理方式与MSMPA相同.但在本文中,追随者子群采用优化算法:
(17)
式中,r5为服从[0.5,1]均匀分布的随机值.
2.4 子群数目自适应策略
在MSMPA中,领导者子群、追随者子群和衔尾者子群的数目始终是各占种群中个体总数的1/3.这样划分比较适合在迭代前期,而在迭代后期,执行局部搜索的衔尾者比例过低将导致局部搜索不够充分,容易造成寻优精度不高.针对此问题,本文利用自适应策略,即算法在前期保持全局搜索能力,同时兼顾局部搜索,而在算法运行后期,局部搜索逐渐增强,同时也兼顾全局搜索,从整体上提高算法的收敛精度.根据适应度排序后,改进后的范围为:领导者子群占比根据迭代次数从[0,1/3]线性变为[0,1/9];追随者子群占比根据迭代次数从[1/3,2/3]线性变为[1/9,1/3];衔尾者子群占比根据迭代次数从[2/3,1]线性变为[1/3,1].
3 仿真试验
3.1 数值仿真环境
本文的仿真试验在操作系统Win10上进行,CPU为lntel(R)Xeon(R)CPU E3-1505M v5@2.80 GHz,仿真软件为Matlab 2019b.
3.2 算法初始参数设置
本研究选择灰狼优化算法(GWO)、海洋捕食者算法(MPA)和多子群海洋捕食者算法(MSMPA)与本文提出的多子群自适应策略海洋捕食者算法(A-MSMPA)进行对比分析.在试验过程中,为确保试验公正可信,统一设定四种算法的初始种群数量为30个,迭代次数为500次,并且其他参数一致.
3.3 测试函数


表1 测试函数
3.4 结果分析
为了保证试验的公正性,本试验对上述四种算法在8个测试函数上分别进行30次运行,不同算法的寻优结果如表2和图1所示.
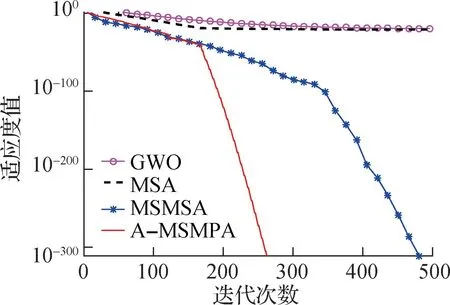
(a) f1收敛曲线

表2 不同算法对测试函数的测试结果
表2中:最优表示所有搜索到的最优解中最小的解,该数据反映算法获得最优解的可能性,其数值越小说明算法寻优效果越好;平均表示这些最优解的平均值,该数据反映算法获得最优解的集中趋势,其数值越小说明算法最优解集中于真实解;标准差表示这些最优解的标准差,该数据反映算法获得最优解的波动程度,其数值越小说明算法最优解波动性小.
由表2可见:单峰函数f1—f4,本文算法的最优、平均和标准差数据几乎全部为0,并且明显小于其他3种算法的相应数据;多峰函数f5—f8,本文算法的最优、平均和标准差数据相较单峰函数的数据差一些,但仍明显小于GWO和MPA,与MSMPA的数据相当甚至更小.
综上所述,本文算法在测试函数中展现了较好的寻优性能,具有更大的可能性获得最优解,且在集中趋势和波动程度方面表现出色.
由图1可见,相较于GWO、MPA和MSMPA,本文算法的收敛精度和速度均表现更为优秀.因此,本文提出的海洋捕食者算法具有出色的寻优能力,可用于解决各类优化问题,是一种有潜力的算法,值得进一步研究和应用.
4 结语
本文提出了一种改进MSMPA,该算法采用动态优化探索和开发阶段的系数,并对追随者子群更新算法进行优化.在此基础上,根据不同阶段自适应调整领导者子群、追随者子群和衔尾者子群的种群数量大小,从而更好地平衡全局探索与局部开发两者的需求.多种算法进行对比试验表明,本文算法在多个优化测试函数上表现出色,能够对各测试函数均达到优异的寻优效果.

