基于ResNet 的和差共阵DOA 估计∗

尤俣良 国洪灿 王 雪

（南京信息工程大学电子与信息工程学院 南京 210044）

1 引言

无线信号波达方向（Direction of Arrival，DOA）估计是一种应用于移动通信和各种雷达系统中的用户定位技术。近几十年来，用天线阵代替窄带波束天线进行DOA 估计已成为普遍现象。为了提高DOA 估计的精度，研究人员在传统算法基础上进行改进，引入更精确的数学模型和优化方法，不断在提高精度、超分辨率和适应低信噪比场景方面取得了显著的进展，也提出了许多信号处理技术，如波束形成、Capon、空间交替广义期望最大化（Space Alternating Generalized Expectation Maximization，SAGE）［1］、协方差矩阵增广（Covariance Matrix Augmentation，CMA）［2］、空间交替广义期望最大化（Space-Alternating Generalized Expectation-maximization，SAGE）［3］等。

最近，深度神经网络（Deep Neural Networks，DNN）展示了其对语音信号处理的强大功能，例如语音分离［4］、自动语音识别（Automatic speech recognition，ASR）［5］等。随后，DNN 也用于DOA 估计，Takeda 和Komatani 使用具有7 个隐藏层的DNN 通过判别训练方法来预测DOA［6］。输入特征是每个频点处相关矩阵的特征向量，实验结果表明，该方法对混响敏感。广义互相关（Generalized Cross Correlation，GCC）被用作一个隐藏层感知器神经网络的特征，结果表明，它对高电平噪声和强烈的混响具有鲁棒性［7］。引入卷积神经网络（Convolutional Neural Networks，CNN）技术，从而为解决DOA 估计问题带来新的方法，其中将短时傅立叶变换（Short-time Fourier Transform，STFT）的相位分量用作CNN 的特征［8］。基于CNN 的方法显示了对噪声的鲁棒性和麦克风位置的小扰动。随着互质阵列技术的应用，功率信号成为新的信号源。然而，它们是相干的，而通常用于估计DOA 的MUSIC 算法要求源是非相干的。尽管空间平滑技术可用于去相干源，但它通常应用于均匀数据。传统互质阵列的差分共阵列存在“空洞”［9］，即缺少一些虚拟阵列元素。

为了解决这个问题，本文提出一种基于残差网络（Residual Network，ResNet）的和差共阵（Sum and difference co-array，SD-CPA）DOA 估计算法。该算法将和差共阵输出的空间平滑矩阵经过数据预处理后生成的特征数据输入残差网络中，将DOA 估计转变为特征数据和DOA 之间的非线性映射关系，通过ResNet对信号分类来实现DOA估计。

2 阵列模型

2.1 互质阵列

传统的互质阵列［9］由两个均匀的线性子阵列组成，它们的阵列间距分别为M和N，如图1 所示。第一个子阵列中有N个传感器，第二个子阵列中有M个传感器。M和N是互质整数，即gcd(M,N)=1，d为阵元之间的距离。为避免空间混叠，d通常设置为λ/2，其中λ是入射信号的波长。传统互质阵列中的传感器放置如下所示：

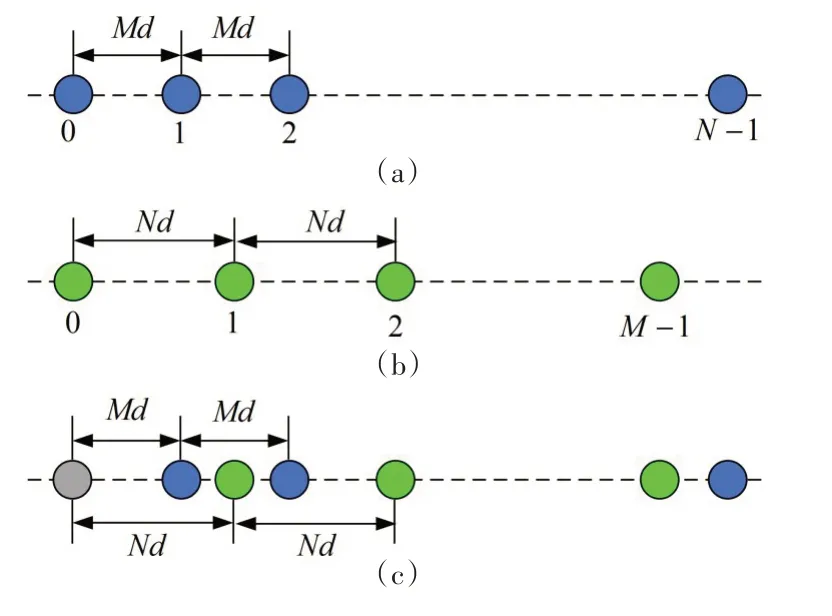
图1 互质均匀线阵

式中，0 ≤n≤N-1，0 ≤m≤M-1。由于这两个均匀线性子阵列的第一个传感器位于同一位置，因此传统的互质阵列中的传感器总数为M+N-1。

在互质阵列中，两个均匀线性子阵的方向向量可以表示为

式中，θk是每个信号的DOA。结合式（2）和式（3）可得，互质阵列的方向向量和方向矩阵为

假设图1 中互质阵列接收的信号为X(t)=AS(t)+N(t)，接收信号的协方差矩阵为Rxx=，对Rxx进行矢量化处理，得

式中，RSS为声源的协方差矩阵，I为单位矩阵转化后的列向量，p为，vec(∙)为将矩阵转化为列向量的操作，⊗表示克罗内克乘积，⊙表示Khatri-Rao积。

2.2 和差共阵

差分阵是互质阵列中两个子阵的实际阵元位置之间的位置间距的集合，它关于原点对称。差分阵是互质阵列经过虚拟化之后产生的，它是PC中的任意两个元素作差得到的虚拟阵列。

传统互质阵列的差分共阵列存在“空洞”，即缺少一些虚拟阵列元素。为了解决这个问题，采用延伸的互质阵列来让差分共阵列获得更长的连续均匀线阵。延伸的互质阵列和传统互质阵列具有相似的阵列布置，只是在第二子阵列中放置更多的传感器，如图2所示。

图2 延伸的互质阵列

通常，经过计算阵列输出的协方差矩阵可以获得差共阵，而和共阵作为主动传感中的虚拟阵列自然产生［9～10］。延伸后的互质阵列产生的和差共阵的数目为2MN+2M+2N-1。但是，此和共阵仅包含交叉和项，而未包含自和项。假设信号的功率为的K个实值源从[θ1θ2…θK]方向撞击阵列，则在阵列的方向矩阵可表示为

在阵列信号处理中，差共阵是在计算接收数据之间的自相关等二阶矩时自然形成的，通过分析式（2～6），令B=A*⊙A，可得

式中，b(θk)和B分别为阵列经过矢量化后得到差共阵的方向向量和方向矩阵。同时，也可以计算出正和共阵Rxx2和负和共阵Rxx3以及他们的矢量化。

由此，我们可以轻松地集成三个新生成的接收数据向量：

式中，z1、z2、z3分别是差共阵、正和共阵和负和共阵的矢量化。

同时，也能得到一个较大的对应阵列流形矩阵：

式中，B1、B2、B3分别是差共阵、正和共阵和负和共阵的方向矩阵。由于向量中存在冗余和无序阵元，必须删除并重新排序一些阵元来重建z，以形成新的向量z'，从而使其对应的B'具有与连续虚拟ULA 的流形相同的表达式。重建的向量z'可以表示为

将新接收到的数向量z'划分为多个向量，将其对应的虚拟ULA 阵列划分为多个重叠的子阵列，然后计算每个分割的接收的向量的自相关矩阵，同时取所有自相关矩阵的平均值，则空间平滑矩阵Rsd：

式中，DOF为所有子阵列的数量，经过空间平滑技术后，可用的DOF为MN+M+N，可以将空间平滑矩阵Rsd的上三角阵作为神经网络的输入，则其输入特征是通过式（12）得到，将式（12）中的上三角阵按照实部与虚部分别展开，得到特征组合序列：

式中，Im(∙)为虚部，Re(∙)为实部。

3 基于注意力的ResNet 的和差共阵DOA估计

在传统的DOA 估计方法中，MUSIC 算法被认为是一种经典典范。该方法在角度域内寻找谱峰，以确定信号源的方向。与其他方法如最大似然法（Maximum Likelihood Method，ML）和加权子空间拟合（Weighted Subspace Fitting，WSF）相比，MUSIC算法在计算方面具有较小的复杂性，这使得其成为一种受欢迎的选择。随着互质阵列技术的应用，功率信号成为新的信号源。然而，它们是相干的，而通常用于估计DOA 的MUSIC 算法要求源是非相干的。尽管空间平滑技术可用于去相干源，但它通常应用于均匀数据。针对这些问题，本文提出了基于ResNet的DOA估计算法［10～11］。

本文提出的算法将ResNet 应用到DOA 估计中，通过和差共阵与ResNet 相结合，能有效解决传统互质阵列中差分共阵缺少一些虚拟阵列元素的问题，该算法将DOA 估计任务转化为输入和输出之间的映射关系，从而实现对信号源方向的精确估计。该算法不受阵列形状的限制，同时还增强在各种不同麦克风阵列设置下的适应性。

3.1 ResNet网络

CNN 是一类深度神经网络，具备卷积层、池化层和全连接层等不同网络组件［12］。CNN 通过堆叠更多网络层，可以更好地从数据集中提取不同级别的特征。然而，CNN模型很难训练，随着网络深度的增加，训练精度越来越饱和，之后开始迅速下降［13～14］。为了克服退化，ResNet 网络被提出来促进CNN 模型的训练。与其他CNN 网络模型相比，ResNet 网络通过添加身份映射来解决退化问题，如图3 中的曲线所示。

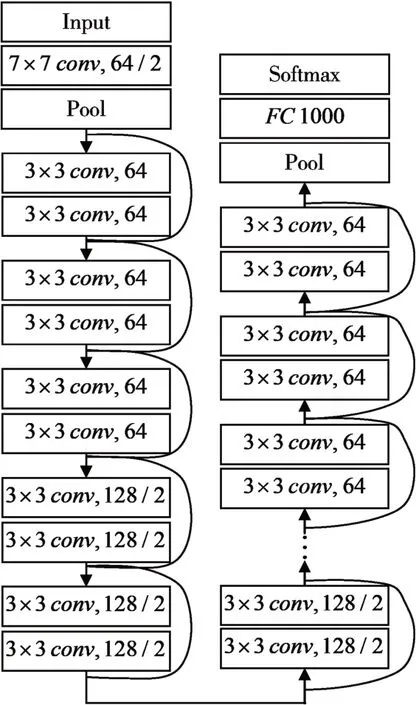
图3 ResNet的网络模型图

相比其他的CNN 网络，ResNet 网络多了残差块，残差块是ResNet 网络的主要基础元素，如图4所示。随着我们深入到具有大量层的网络中，计算变得更加复杂。这些层相互叠加，每一层都试图学习所需函数的一些底层映射。图4 中，x作为第一层的输入，G(x)表示从第一层输入到堆叠层输出的映射。在模型训练期间，学习所需映射G(x)的问题可以转化为学习残差映射函数F(x)，其中F(x)=G(x)-x。鉴于原始映射函数变为F(x)+x，对应于F(x)的堆叠层的权重可以为零，以模拟层与层之间的“快捷连接”。通过利用残差网络，即使层数增加到1202，也可以优化CNN 模型，但是使用这种更深的网络往往会因为过拟合而导致较低的测试精度。

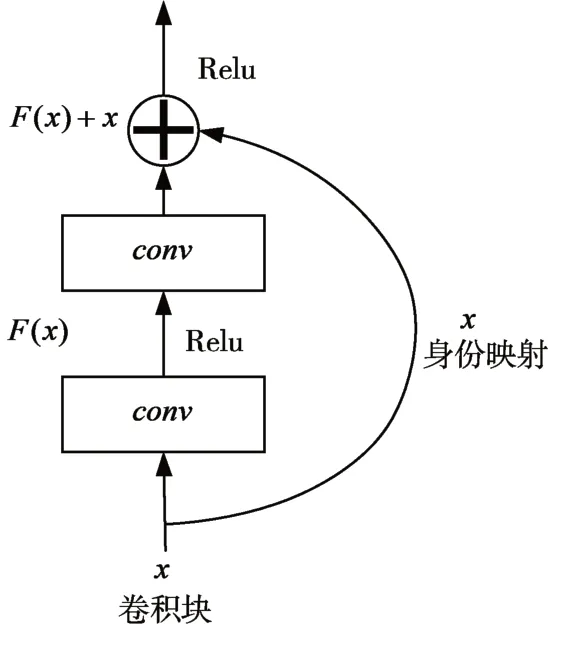
图4 残差块的结构图

3.2 基于ResNet的DOA估计

所提出的基于ResNet的DOA 估计可以看作是一个阵列输出信号和DOA 之间的映射函数，如图5所示。将DOA 估计分为两个阶段：在第一阶段中，对通过和差共阵获得的空间平滑矩阵Rsd进行数据预处理来获得特征数据y；第二阶段中，将特征数据y与生成的物理DOAθk形成训练数据集，作为训练样本输入基于注意力机制的ResNet，获特征数据y与生成的物理DOAθn之间的映射函数，即

图5 基于ResNet的DOA估计

式中，θk为训练角，y为特征数据。因此，通过训练DOA 估计网络，从而掌握阵列输出与相应DOA之间的非线性联系。

为了获得估计的DOAθk，选择ReLU函数作为激活函数，损失函数基于交叉熵概念，即

式中，M表示类别数，为符号函数（0 或1），pic为观测样本i属于类别c的预测概率。

3.3 评估指标

本实验采用均方根误差（Root Mean Square Error，RMSE）作为评估标准，将MUSIC算法和采用的算法进行对比，以评估算法的准确性和稳定性。RMSE的公式表达为

式中，N表示为数据样本总数，表示为入射方向的估计值，xn表示为入射方向的真实值。

4 实验与仿真

实验仿真设置在一个尺寸为5.5m×2.3m×3.3m 的消音室中进行，如图6 所示，采用M=4 和N=5 的均匀线性互质阵列，则物理传感器的总数为M+N-1=8，生成的和差共阵的数目为2MN+2M+2N-1=57，经过空间平滑技术后，可用的DOF为MN+M+N=29，阵元之间的间距设置为0.17m。仿真在TensorFlow 平台上实现，其中ResNet的学习率设置为0.001，训练周期为1000。

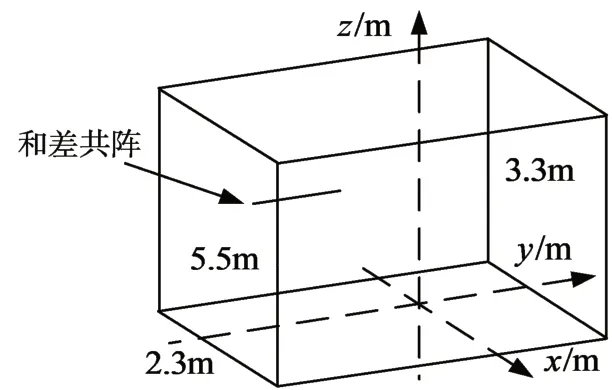
图6 仿真环境

本实验首先比较MUSIC 算法和本文采用算法在和差共阵中DOA 估计的性能。设置信噪比SNR为0 dB，快照数为100。图7 和图8 分别为MUSIC算法和本文采用算法的频谱图，可以发现和差共阵可以识别频谱中的所有源，这证明了其使用数量少得多的物理传感器识别大量源的有效性。通过对比图7 和图8 可以发现，本文采用的算法能更为精确地识别所有的源。

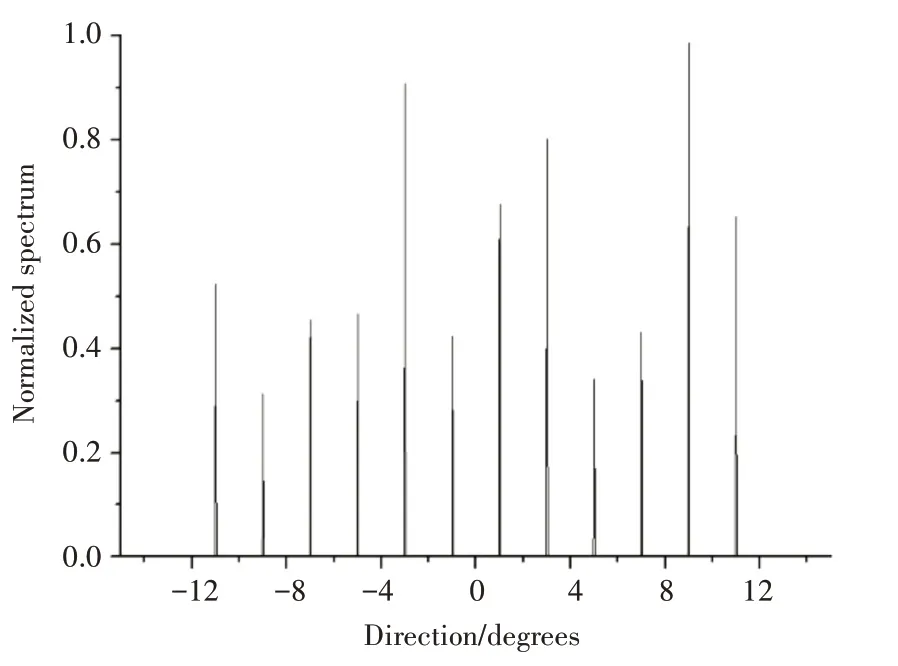
图7 MUSIC算法频谱图

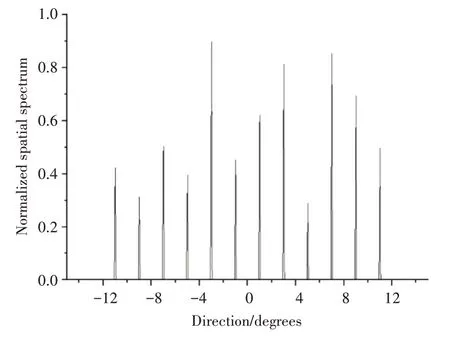
图8 本文采用算法的频谱图

接着分析SNR 和快照数的变化对本文采用算法的影响。图9 和图10 分别为SNR 的变化和快照数的变化对MUSIC 算法、SVR 算法以及本文算法的DOA 估计的影响。图9 中，SNR 以2.5 dB 为步长在-10 dB～10 dB之间变化。从图示可知，在SNR高于-1.2 dB 时，MUSIC 算法表现出稍高的估计精度；然而，在低信噪比情况下，基于SVR 算法和本文提出的方法的DOA 估计性能更佳，特别在较低信噪比下，本文算法展现出优异的抗干扰能力。

图9 SNR的影响

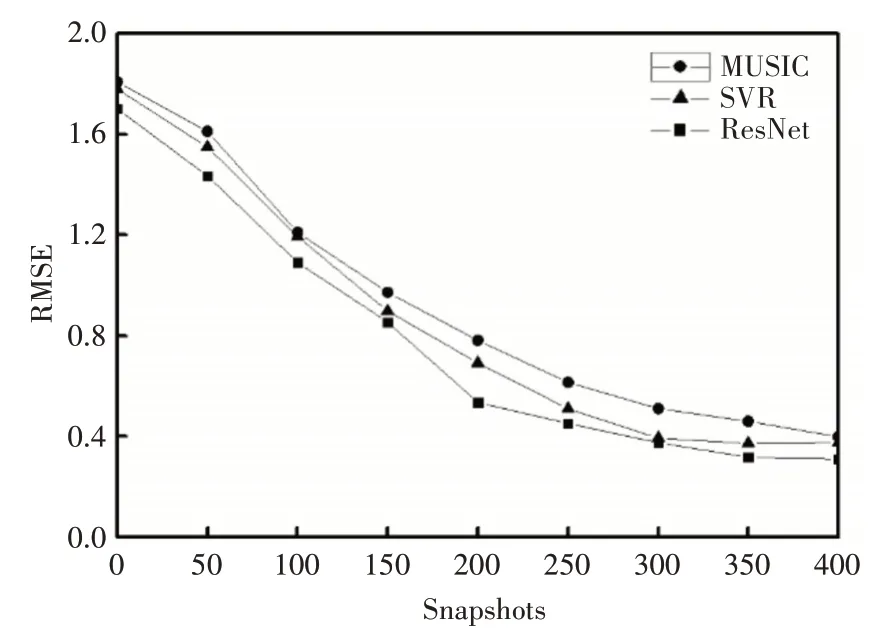
图10 快照数的影响

图10 为快照数的变化对MUSIC 算法、SVR 算法以及本文算法的DOA 估计的影响，采样点数以50 为步长在0～400 之间变化。随着采样点数的增加，三种算法的RMSE 逐渐减小，这表明随着样本数量的增加，DOA估计的性能得到了提升。

5 结语

本文采用ResNet 与和差共阵结合的方法来解决传统互质阵列的差分共阵存在“空洞”的问题。通过仿真可以得出，采用基于ResNet 的和差共阵的DOA估计技术能够有效提高了DOA估计的准确性和适应性，同时也能减少对于阵列阵元的需求。然而，本文中采用的DOA 估计算法在神经网络的训练阶段中，数据需求较大，在后期还需不断改进神经网络结构或采用更适宜的神经网络，减少数据需求。