基于经验小波变换的畸变信号电量计量研究∗

冯 昆 徐天奇 李 琰 王兴明 朱梦梦

（1.云南省高校电力信息物理融合系统重点实验室（云南民族大学） 昆明 650504）（2.南京弘毅电气自动化有限公司 南京 210039）（3.云南电网有限责任公司电力科学研究院 昆明 650217）

1 引言

如今，现代电力系统中各种非线性负载，如感应加热炉、电力机车、电力电子开关设备、电化工设备等，占有率迅速增加。这类负荷的增加造成供电电压不对称程度和波动性加剧，从而造成了大量谐波信号的产生［1～3］，导致电网的电能质量日趋恶化，电网信号畸变严重。

另一方面，电压电流信号中除了基波外还掺杂大量的准周期、时变、非平稳的畸变信号，严重影响其他用户的供电质量［4～6］。现在电网所使用的计量方案大多还是只计量基波电压与基波电流所产生的电能，但负荷基波信号和畸变信号也有电能的交换。由于目前国际上尚无统一的针对畸变信号电能计量的标准，使得对非线性负载用户的惩罚措施缺失，对电网造成了巨大经济损失。因此研究和完善对电网非平稳畸变信号的电量计量理论和方法是现在急待解决的问题［7～8］。

现在的电能计量设备使用的时-频分析工具大多是快速傅里叶变换FFT（Fast Fourier Transform）。FFT对稳态信号有较好的频域分辨能力，但是对电网畸变信号的分析却暴露出来“旁瓣”和“频谱泄露”等问题，难以适应当前复杂的电力系统畸变信号。短时傅里叶变换STFT（Short-Time Fourier Transform）虽然能够结合时域和频域信息对畸变信号进行分析，但是窗函数一经选定，时频分辨能力就固定了下来，检测精度有所限制。小波变换WT（Wavelet Transform）虽然解决了STFT 的时频分辨率固定的问题［9］，但是小波基和分解层数的选取需要根据实际场景具体选择。S 变换作为STFT 和WT 的延伸具有不错的时频分析能力和抗噪性，但是其和STFT一样受约束于海森堡测不准原理。希尔伯特-黄变换HHT（Hilbert-Huang Transform）的自适应能力强，不受海森堡测不准原理的约束，同时不存在非线性交叉项，但是依旧存在模态混叠的现象，数据序列两端会出现发散现象导致其难以应用到实际。

文献［10］提出了一种新的信号分析方法经验小波变换EWT（Empirical Wavelet Transform）该方法在经验模态分解EMD（Empirical Mode Decomposition）和小波变换的理论框架发展而来，运算效率较高，现已被广泛应用到工程信号分析，故障诊断等领域［11～12］，并取得不错的效果。文献［13～14］利用小波变换对畸变信号进行电量计量，需要进行小波基和分解层数的选择，自适应能力较差。文献［7］提出基于形态小波对非线性信号进行电量计量，但是也有可能存在各频带间的频率混叠现象，也未能实现自适应检测。文献［15～16］提出改进S变换和基于二进制采样快速S 变换算法，有较强的时频分析能力但是依旧受制于海森堡的测不准原理。

综上所述，现有的计量方法大多自适应能力不强，容易出现频率混叠现象，造成计量误差较大。

针对上述问题本文首次提出一种基于经验小波变换的畸变信号电量计量的新方法，使用经验小波变换对电网的畸变电压电流信号进行自适应性分解，重构基波和畸变的电压电流信号，从而方便进行电量计量。这种方法不仅提高了小波变换的自适应性，同时保留了小波变换时频同时局部化的优点。

2 畸变信号的电量计量

2.1 电力系统中的畸变信号的产生

理想情况下电网应该以固定的50Hz频率和标准正弦波形向负荷提供电能，但是由于日益增多的非线性负荷存在使得电网的电压电流发生畸变。当非线性负荷被施加标准正弦波形的电压或电流时，它就会在与电网的连接点形成畸变电压或电流，引起电网电压或电流的畸变，造成设备过热、设备绝缘破坏等不良后果。按照不同的负荷性质，非线性负荷大致可以分成铁磁饱和型负荷、电子开关型负荷、电弧型负荷三种［15］。此外，电网中还会产生一些随机的非线性信号，例如：系统远端发生故障、大容量电机启动会产生电压的暂降或者暂升；线路负载和电容器组投切会有暂态震荡的产生。

2.2 畸变信号下的功率理论计算方法

本文考虑非线性负荷单相畸变信号的电量计量，假设电网中的单相电压电流信号构建为［9］

式中u0（t）、i0（t）分别为直流电压电流信号；u1（t）、i1（t）分别为基波电压电流信号；Σuℎ(t)、Σiℎ(t)分别为谐波电压电流信号；Σup(t)、Σip(t)分别为间谐波电压电流信号；uc（t）、ic（t）为其他形式的信号。

去除电压电流基波分量，电压畸变分量us（t），电流畸变分量is（t）分别为

根据功率计算公式，不同的功率分量为

式中p1（t）为基波功率；p1s（t）为基波电压信号与畸变电流信号作用产生的功率；ps1（t）是畸变电压信号与基波电流信号作用产生的功率；pss（t）为畸变电压信号和畸变电流信号产生的功率。

3 基于经验小波变换的畸变信号电量计量算法

经验小波变换是一种非递归的计算，首先将待观测的畸变信号从时域转换成频域做归一化处理并自适应分割频带，在各个频域中进行经验小波变换，将原始畸变信号分解为一组AM-FM（Amplitude Modulated Frequency Modulated）分量之和，假设可以分解为N个AM-FM分量，其变换可分为3步［17］。

1）频谱划分

首先确定待观测信号N 的个数。根据幅值的大小对信号频谱的极大值幅值序列进行降序排列，并对其设置阈值为MM+α（M1-MM），α∈（0，1）代表相对幅值比。将大于该阈值的极大值记为主极大值，主极大值的个数即为N；频谱中相邻两个主极大值对应的频率Ωn和Ωn+1的重合点即为划分频谱边界ωn，其中n=1，2，…，N-1，ω0=0，ωN=π。

2）小波函数与尺度函数的构造

参照Meyer 小波的构造方法构造经验尺度函数φn（ω）以及经验小波函数ψn（ω），其可表达为

3）经验小波变换与逆变换

将原信号f（t）同构造好的经验尺度函数以及经验小波函数进行内积运算，算出近似系数(0,t)以及细节系数(n,t)。

对原信号的重构可以表示为

其中“*”为卷积运算。由信号f（t）分解所得的经验模态函数ck（t）定义为

通过计算畸变电压、电流的各频段成分的经验小波系数，并带入重构方程，即可分别得到基波电压、畸变电压，基波电流、畸变电流。可通过有功功率的计算公式：

分别可计算出功率P1，P1s，Ps1和Pss。

综上所述基于经验小波的电能计量过程如图1所示。

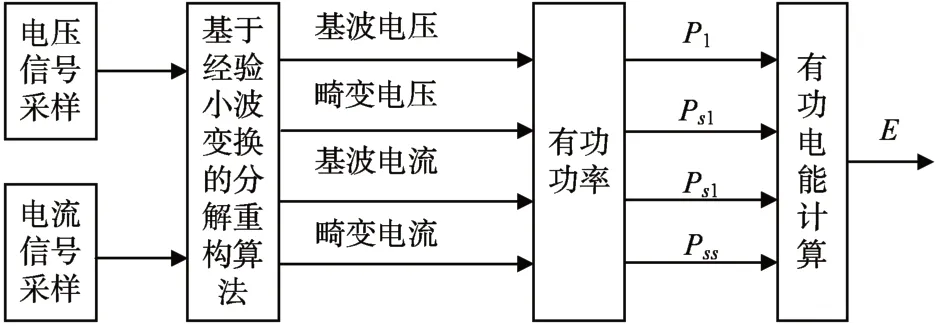
图1 畸变信号电量计量流程图

4 基于经验小波变换的畸变信号电量计量仿真分析

根据实际对地铁、高铁、电弧炉等非线性负荷的采样波形调查分析可以发现：非线性负荷的波形主要以奇次谐波为主，谐波的幅值随着谐波次数的增加而大幅度降低，地铁、高铁等动态负荷的起步、加速、减速等操作也会对电网信号产生扰动［18］。而且非线性负荷从电网吸收基波功率并向电网反送谐波电能。针对非线性负荷的这种信号特征，本文构建了单相稳态畸变信号和时变畸变信号用来模拟此类负荷对电网信号的影响，并对这两种信号分别进行EMD、WT、EWT 的分解与重构，通过重构信号计算P1，P1s，Ps1和Pss。

4.1 稳态畸变信号仿真分析

如前所述，本文首先构建电网电压电流信号，该信号包含稳态基波、2 次、2.9 次、3 次、3.1 次、3.5次、4 次、5 次、7 次和9.5 次谐波和间谐波的仿真分析。具体的信号表达式如下：

式中u（t），i（t）分别是所构造的稳态畸变电压信号和电流信号，f0是基波50Hz。以6400Hz 的采样频率对仿真信号进行采样分析，共采样0.6s的离散数据。

首先对基于式（16）和式（17）构建的畸变电压电流进行EMD 分解。仿真发现，由于电压信号的谐波和间谐波幅值相比于基波幅值较小，故无法进行EMD 分解。电流信号进行EMD 分解后无法区分基波信号，故不能进行稳态畸变信号电量计量。

WT方法仿真过程中通过使用不同小波基和分解层数对比发现使用Daubechies40（DB40）小波基对畸变电压电流信号进行10 层分解可以较准确的分离出基波50Hz 信号，DB40 小波具有很高的消失矩阶数和支撑长度。使用小波变换的逆变换分别重构基波和畸变的电流电压信号，重构信号对比结果如图2～5。可观察到重构的基波电压信号和基波电流信号存在严重的“端点”效应，在端点处存在畸变，相比于原始基波信号，幅值不能准确还原。重构的电压畸变信号和原始畸变信号有较大的差别，电流畸变信号在端点处还原也不准确。

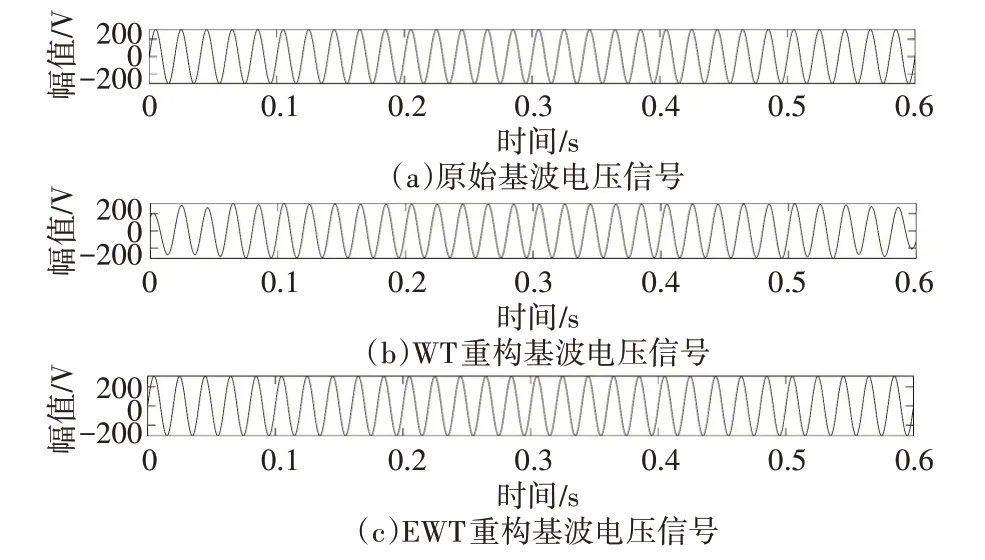
图2 WT、EWT重构稳态基波电压信号对比

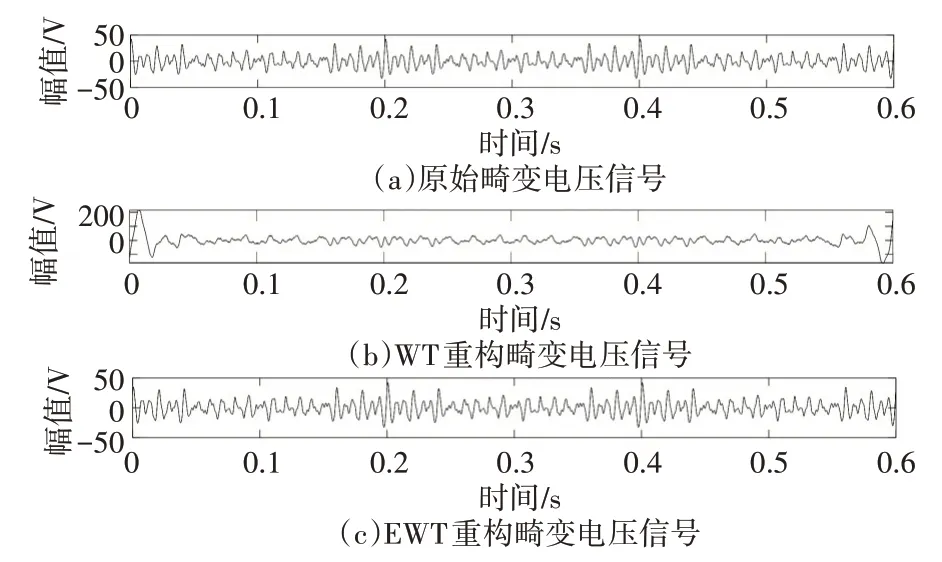
图3 WT、EWT重构稳态畸变电压信号对比

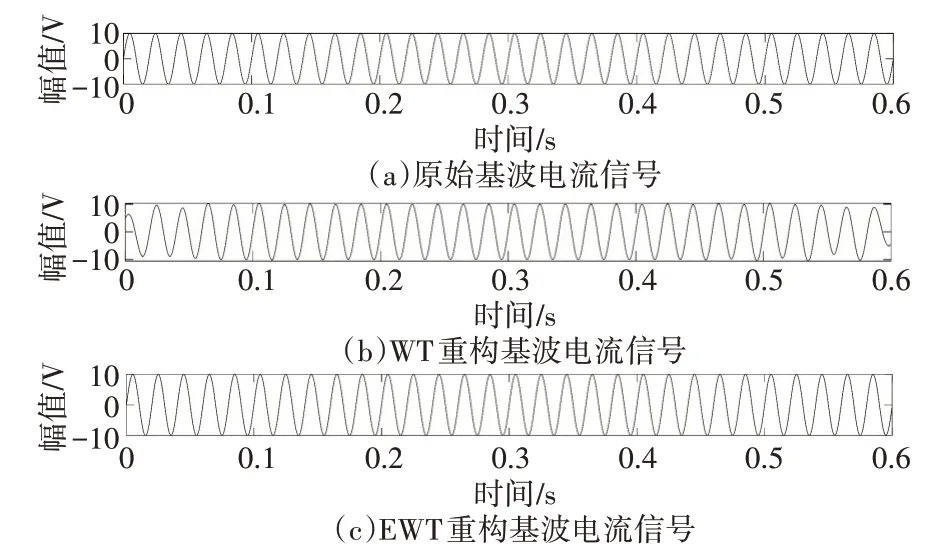
图4 WT、EWT重构稳态基波电流信号对比

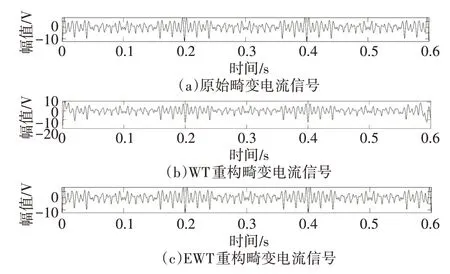
图5 WT、EWT重构稳态畸变电流信号对比

使用EWT 分解仿真信号能够首先进行自适应的频谱划分，将原始畸变信号按照频谱图自适应分解为10 个模态然后再对每个模态进行小波变换。根据信号本身的频谱特征实现了分解的自适应性，不用实验选取分解层数。重构信号对比结果如图2～5，即使在端点部位，和原始信号对比发现有着更好的还原效果。

根据功率公式（5）可以使用重构的信号计算出P1，P1s，Ps1和Pss。如表1、2。

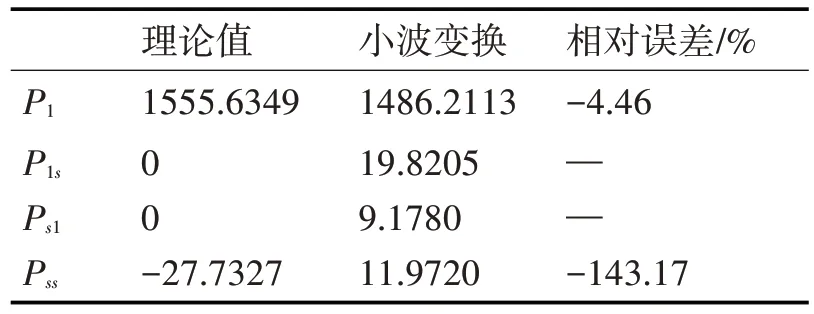
表1 稳态畸变信号小波变换功率计量结果

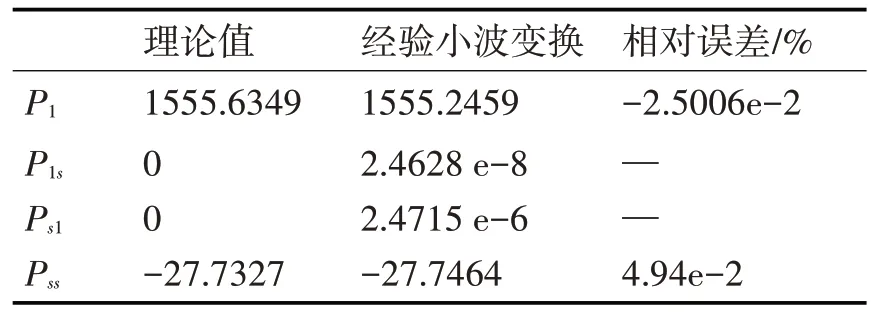
表2 稳态畸变信号经验小波变换功率计量结果

由表1、2 可知：与使用WT 分解对比可得使用EWT 在每一个功率分量上算得的功率相对误差明显更低。传统小波变换产生高于经验小波变换的误差地原因是存在频谱混叠和“端点”效应。不能较好的分离出不同的谐波信号，重构的基波和畸变信号和真实信号在起始位置和结束位置误差较大，并且重构的畸变电压信号和真实畸变信号相差过大致使P1、Pss等存在着较大的误差。

4.2 时变畸变信号仿真分析

时变谐波信号和暂态震荡信号是是电网中非线性负荷常见的两种暂态信号，参考文献［9，17］构造基波+时变谐波+暂态震荡的复合畸变信号数学模型为：

式中u（t）、i（t）分别是所构造的时变畸变电压信号和电流信号，f0是基波50Hz。构造的暂态信号2次、2.9次、3次、3.1次、3.5次、4次、4.5次、5次谐波均产生于0.2s 上升，0.4s 后下降一半。6 次衰减震荡谐波电流信号产生于0.4s，同样以6400Hz 的采样频率对所构建的信号进行采样分析，总共的采样时间为0.6s。用于模拟电网中的复合扰动。

对构造的信号使用EMD 分解电压信号同样由于畸变信号相对于基波信号幅值较小无法进行分解，故无法完成时变畸变信号的电量计量。

WT方法仿真过程中通过使用不同小波基和分解层数对比发现使用Daubechies40 小波基对畸变电压信号进行9层分解，对畸变电流信号进行10层分解，可以较准确的分离出基波50Hz 信号。小波变换分解结果依旧存在模态混叠的现象，重构时变畸变信号如图6～9。由图可知重构的基波和畸变信号在初始位置和结束位置存在明显“端点”效应，并且重构的畸变电压信号和原始畸变电压信号差别较大。

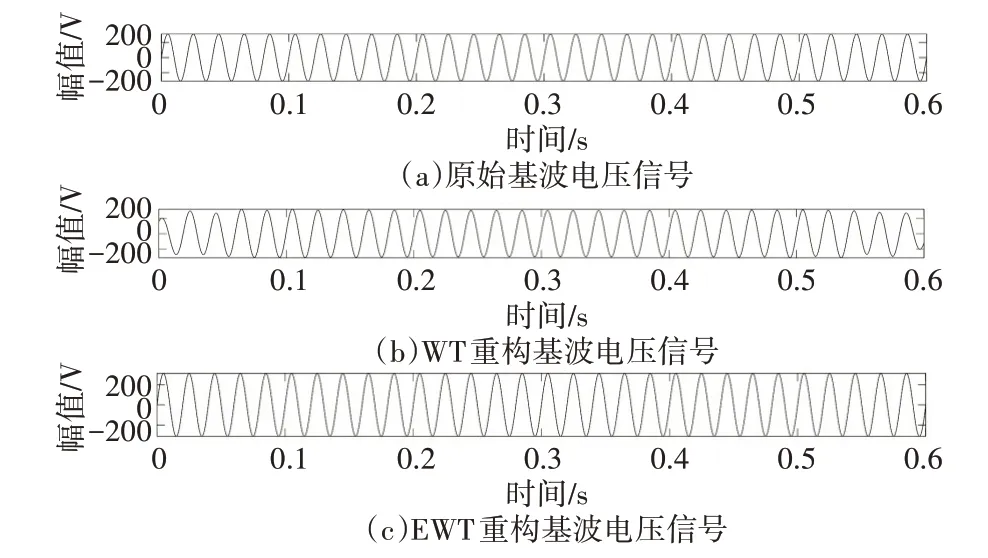
图6 WT，EWT重构时变基波电压信号

图7 WT，EWT重构时变畸变电压信号

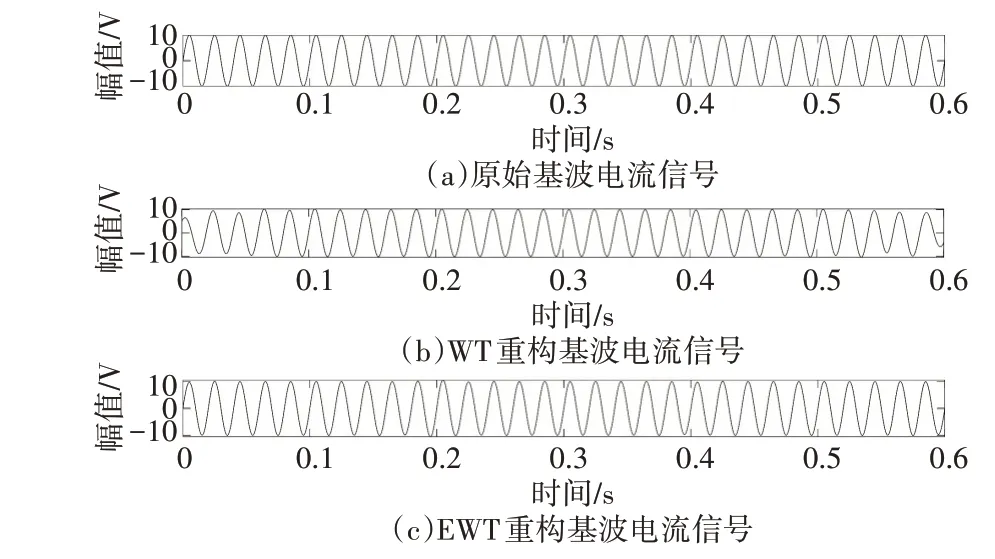
图8 WT，EWT重构时变基波电流信号

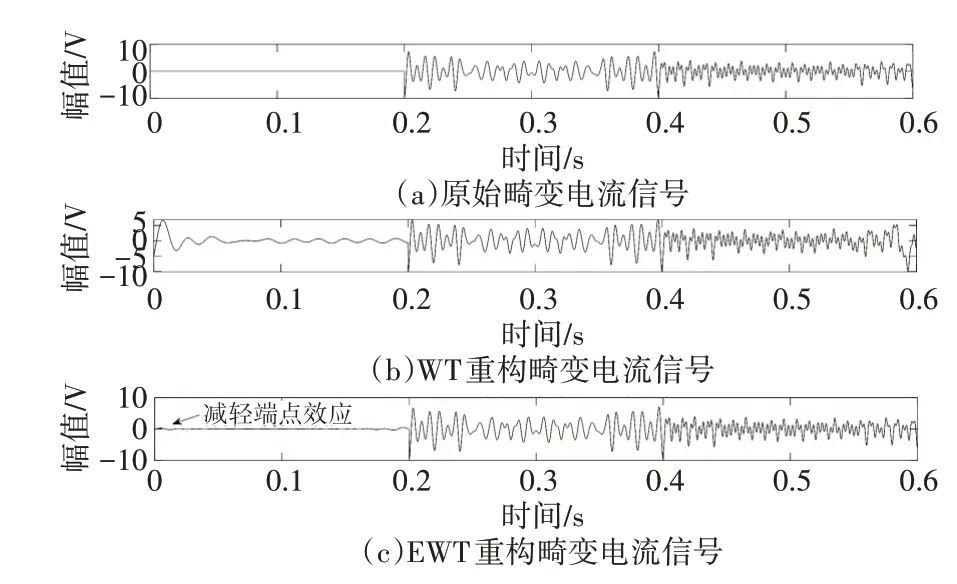
图9 WT，EWT重构时变畸变电流信号

EWT 对复合信号进行自适应分解，将电压频谱图分解为9 个模态，电流频谱图分解为10 个模态。重构基波信号和畸变信号如图6～9，和WT 重构的信号相比有着更好的还原效果，重构的波形相比于小波变换的波形更为标准，且在时域上也有很好的定位能力，在0.2s 和0.4s 时准确地反应出畸变信号的起始时间和变化时间，并减轻了小波变换的“端点”效应。

依据WT、EWT 重构的电压电流基波信号和畸变信号，根据式（5）分别计算出P1（t），P1s（t），Ps1（t），Pss（t）如表3、4所示。

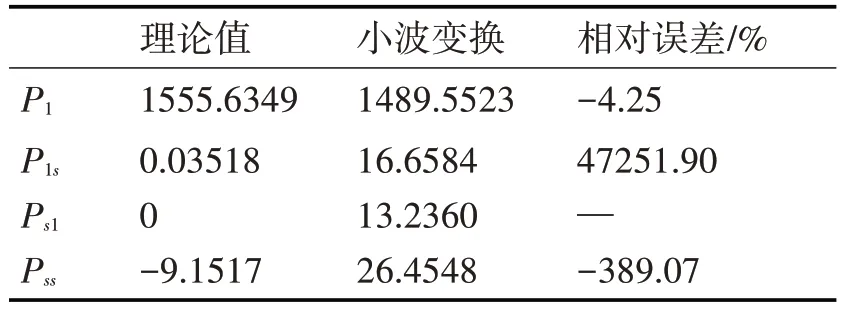
表3 时变畸变信号小波变换功率计量结果

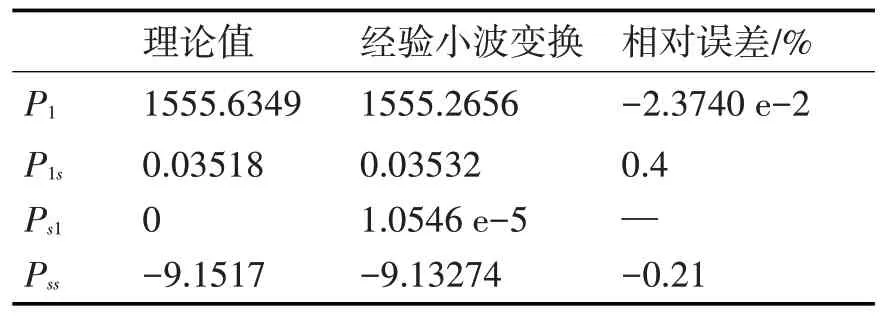
表4 时变畸变信号经验小波变换功率计量结果

将本文使用经验小波变换与文献［7］使用形态小波方法和文献［13］使用小波变换相对比。文献［7］两个实验的P1相对误差是0.29%和-0.37%，Pss两个实验的相对误差是-0.41%和0.57%，文献［13］两个实验的P1相对误差是-3.6%和-0.82%，Pss两个实验的相对误差是4.4%和5.2%，相比下本文使用的方法相对误差更低。由表3、4 知与小波变换相比在每个功率分量上的相对误差都更低，而且从重构信号可以看出经验小波变换在一定程度上减轻了“端点”效应，有着更好的还原效果。更能自适应的分析电网的复杂信号，同时也能准确地计量出畸变信号的功率值。

5 结语

随着非线性负荷的大量使用，电网中出现了大量的畸变信号，严重影响了电量计量的准确性。本文针对这一问题，提出了一种基于经验小波变换的非线性负荷畸变信号电量计量方法，分别在稳态畸变信号和时变畸变信号环境下，将经验小波变换和使用DB40作为小波基的小波变换进行对比仿真实验，得出以下结论：经验小波变换能够实现对电网常见畸变信号的自适应的分解分析，不用设置分解层数能够根据频谱图自适应进行分解，准确分解出基波信号和各次谐波信号，明显减轻了小波变换的模态混叠现象，同时有着较好的时域定位精度，能精准定位畸变信号起始和结束时间，并且能够准确重构出基波信号和畸变信号，从而可以进行准确的电量计量，降低了传统小波变换的计量误差，减轻了小波变换的“端点”效应。