无人机遂行编队飞行中的纯方位无源定位
周宏兵, 刘力歌, 赵迦勒, 赵松曼
(1.南阳师范学院 数学与统计学院,河南 南阳 473061; 2.南阳师范学院 物理与电子工程学院,河南 南阳 473061)
0 引言
无人机的无源定位在民用和军事领域(如救援、探测等)有着广泛的应用。由于单架无人机探测能力不够,许多研究者转向无人机集群控制和编队飞行的相关研究[1-4]。无人机集群在遂行编队飞行时,为避免外界干扰,应尽可能保持电磁静默,减少向外发射电磁波信号。为保持编队队形,拟采用纯方位无源定位的方法调整无人机的位置,即由编队中某几架无人机发射信号,其余无人机被动接收信号,从中提取出方向信息进行定位,从而调整无人机的位置。 编队中每架无人机均有固定编号,且在编队中与其他无人机的相对位置关系保持不变[5]。由于无源定位技术使工作平台不辐射电磁信号,只通过测量其他辐射源发射的电磁信号参数来确定其位置的一项技术,因此相对于有源定位,没有电磁辐射,具有隐蔽性更好、生存能力更强的优点[6-8]。
1 模型假设
为尽量排除各种无关因素对建立的数学模型产生的误差,我们做如下假设:
(1)无人机在空中运动时忽略天气的影响;
(2)无人机电力充足;
(3)无人机可以正常接收信号;
(4)圆形编队始终在同一平面上。
2 模型建立与分析
编队由 10 架无人机组成,形成圆形编队,其中 9 架无人机(编号 FY01~FY09)均匀分布在某一圆周上,另外1架无人机(编号 FY00)位于圆心(见图1)。无人机基于自身感知的高度信息,均保持在同一个高度上飞行。
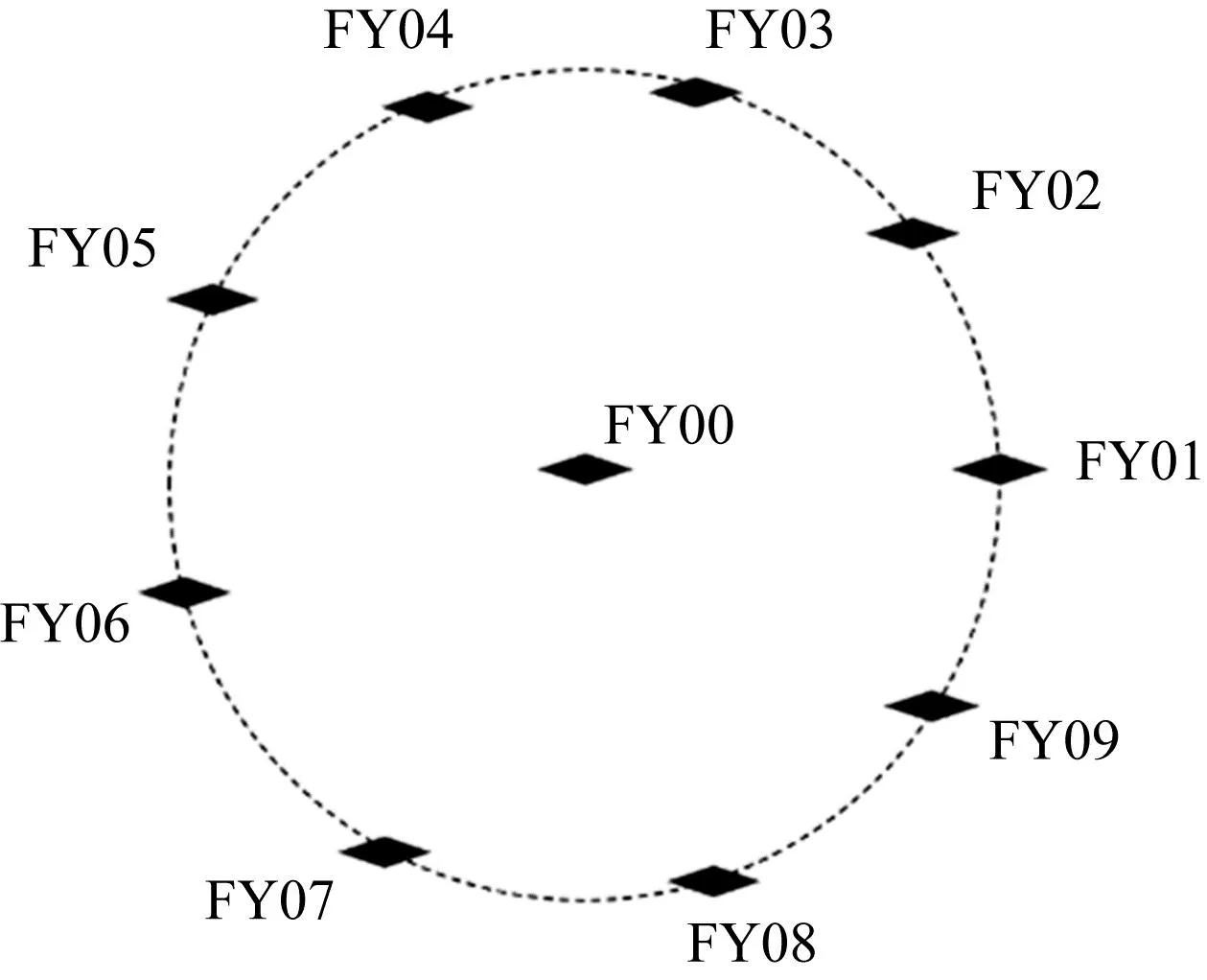
图1 圆形无人机编队示意图

图2 有偏差的无人机平面示意图
2.1 建立被动接收信号无人机的定位模型
以编号FY00无人机为极点,FY00和FY01连线为极轴,建立极坐标系。设位置略有偏差的无人机为点P,其极坐标为(a,θ),求出点P的极坐标即可得到被动接收信号无人机的定位。由特殊到一般,先研究其中一种情况:位于圆心的无人机FY00和编队中的FY01,FY03无人机发射信号,其中β=80°。为方便观察,以下均以β=80°作图,其余角度同理,但并不代入β=80°,得出被动接收信号无人机的极坐标通式。因为无论哪2架无人机发射信号,它们的算法都是相同的。
由题干已知无人机均保持在同一个高度上飞行,则可以把它们视为一个平面,画出此模型的平面示意图,如图 2所示。
通过观察此平面示意图得出。
由(a,θ)可知,OP=a,∠AOP=θ。
在△OAP中,由正弦定理可得
(1)
即
(2)
易知,∠BOP=β-θ。
在△OBP中,由正弦定理得
(3)
即
(4)
联立(2)(4)得
(5)
解得
(6)
2.2 实现无人机的有效定位的模型
2.2.1 通过圆周角确定所需无人机的架数
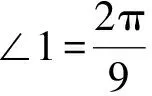

图3 无人机编队示意图划分
图4 圆周角与圆心角关系

接着判断找到的圆周角是锐角还是钝角,并求出发射信号的无人机的编号通项公式。具体流程如图5所示。

图5 获得无人机编号流程
综上,发射信号的无人机位置无偏差,除FY00和FY01外,还需要1架无人机发射信号即可实现无人机的有效定位。
2.2.2 运用正弦定理调整无人机的位置
要确定其他9架无人机位于某个以FY00为圆心的圆周上,可以先由任意2架无人机发射信号,运用正弦定理得到1架在某个以FY00为圆心的圆上(即无偏差)的无人机的方向信息,即角α1和α2的大小。
在一个三角形中,知道两边及其夹角即可算出三角形的另外一个角的角度。
由余弦定理得:a2=b2+c2-2bccosθ。
联立得出α的度数。
令其为该无人机的标准角,则该无人机可以将原本接收到的角α1和α2各自逐渐调整到对应的标准角的大小,最终可以调整到理想位置。同理,先找出2架调整到理想位置的无人机并固定位置,再以这2架无人机和FY00为发射信号的无人机,找出其余7架无人机应在的位置所对应的标准角,使其余7架无人机调整到理想位置。
针对其他队形编队,与上述思路类似,先根据2架无人机确定1架无人机在理想位置时接收到的α1,α2值,再进行调整,使其调整到理想位置。同理,也可以调整另1架无人机到理想位置。由此,令这2架无人机和FY03为发射信号的无人机,找出其余几架无人机理想位置对应的α1,α2值,使其余几架无人机调整到理想位置。
3 算例分析
以下以 2022 年数学建模试题B题的实验数据进行算例分析。
3.1 编号为FY00和FY01的无人机以及若干编号未知的无人机向某位置略有偏差的无人机发射信号,另需几架无人机才能实现无人机的有效定位?

图6 圆周角为钝角的情况
3.2 1架无人机位于圆心,另9架无人机均匀分布在圆周上,当初始位置略有偏差时,给出调整方案,将有偏差的无人机调整到理想位置。
若要确定其他9架无人机位于某个以FY00为圆心的圆周上,可以先根据2架无人机确定1架无人机在以FY00为圆心的圆周上,由此可以得到在以FY00为圆心的圆弧上的2架无人机,再以这2架无人机和FY00为发射信号的无人机,找出其余7架无人机应在的位置所对应的α1,α2值,使其余7架无人机调整到理想位置。
以下过程均由此法代入具体数值计算。
(1)以FY00,FY01和FY03为发射信号的无人机。


图7 无人机初始位置与理想位置示意图
∠COB1=∠AOC-∠AOB1=40.21°。

综上可得α1,α2的度数,即可确定FY02在以FY00为圆心、长度98为半径的圆周上,FY02在此位置时无偏差。当FY02接收到的方向信息调整为与无偏差时的方向信息相等时,FY02即可回到理想位置。
(2)同理,以FY00,FY01和FY03为发射信号的无人机使FY04回到理想位置。
接着,因上文已经确定了FY02和FY04的位置,以FY00,FY02和FY04为发射信号的无人机,找出其余7架无人机应在的位置对应的α1,α2值,使其余7架无人机调整到理想位置。
接下来以将编号为FY03的无人机调整到理想位置为例求出α1,α2(如图8)。在△OB1C1中,由余弦定理得
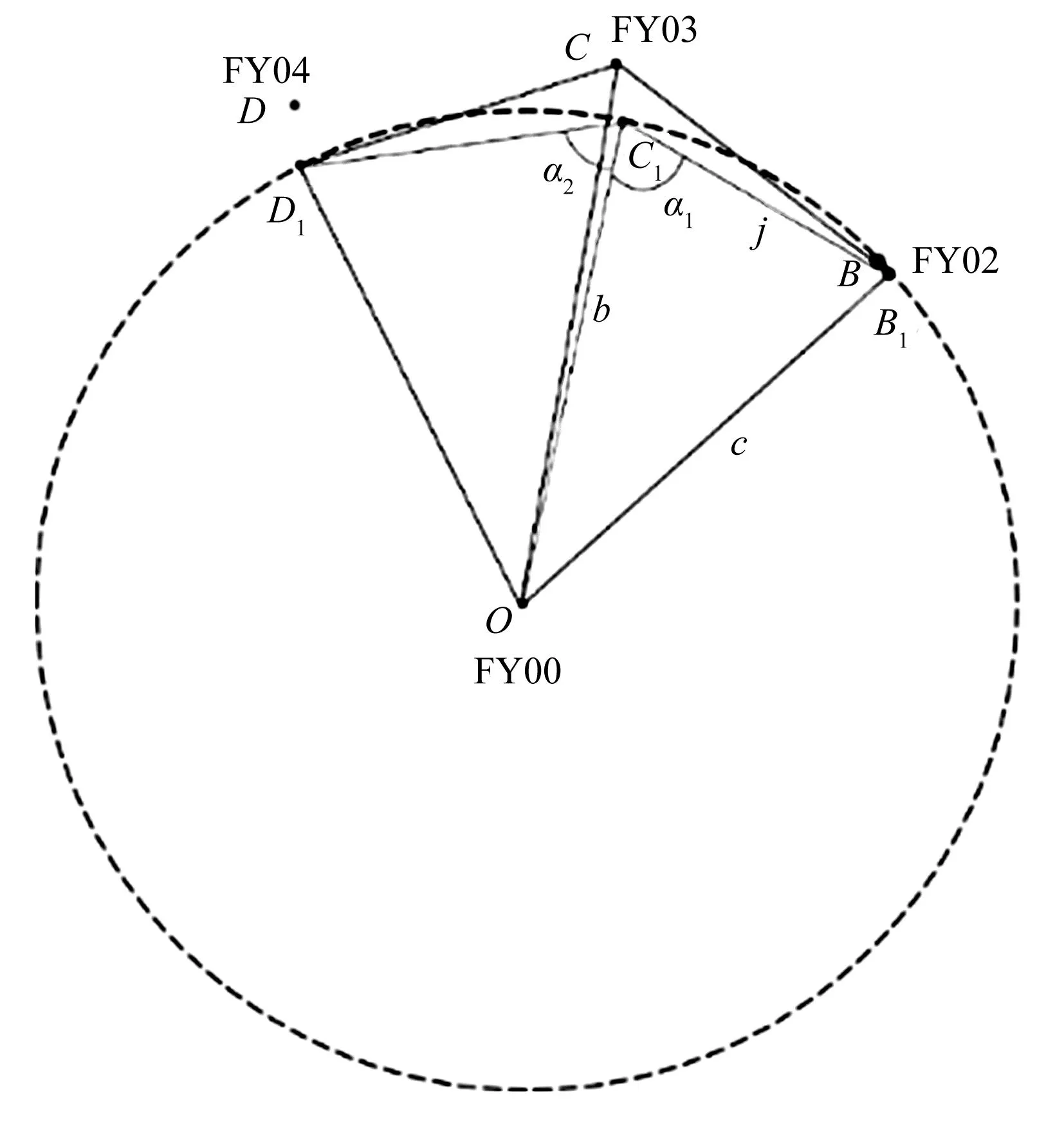
图8 编号为FY03的无人机调整到理想位置示意图
再由正弦定理得
则
同理,在△OC1D1中,由余弦定理和正弦定理可得α2。
其他几架无人机的理想位置对应的α1,α2也是同样的求法,它们对应的α1,α2的值如表1所示。由此即可把其他几架无人机根据α1,α2的值调整到理想位置。

表1 无人机理想位置对应值
4 结论
纯方位无源定位不仅在民用领域具有广泛的应用,例如光纤通信、信号处理和车辆定位导航等,而且在空域预警、海域监测、地面非法入侵和隐蔽通信等国防领域也做出了巨大的贡献。本文在研究纯方位无源定位过程中,通过对无人机之间的角度进行分析,我们可以在不同情况下解决相应的问题。

