动态周期事件触发机制下DC-DC变换器切换鲁棒控制

黄 娟,刘独玉

(西南民族大学电气工程学院,四川 成都 610225)

随着智能控制、通信技术以及控制理论等各方面的飞速发展,人们面临着日益复杂的控制问题,因此需要对系统进行更高的精度控制.通过将控制原理与计算机技术相结合,使其达到自动化控制的目的,是控制系统的发展方向.在实际系统中既存在连续变化的过程,也存在突变的现象,这样的系统更适合采用混杂系统来描述,并通过对混杂系统施加合适的控制方法从而取得预期的控制效果.切换系统是一种很重要的混合系统,几十年以来,切换系统因其固有的特性及其在电力电子[1]、网络化控制系统[2]、生物生态系统[3]等领域的应用受到了广泛关注.

由于现代计算机与微芯片科技的快速发展,现代控制工程中进行大规模计算成为可能,这促进了对采样数据控制系统的研究[4].在已有切换系统稳定性分析和控制器综合的研究成果中,所采用的控制器一般基于连续通信方案[5].这种方案会造成不必要的信息传输和计算资源的大量使用.因此,为了尽量减少损失,事件触发控制策略被广泛应用于各种系统.从已有资料可看出,使用事件触发的系统通常都是混杂系统[6]、扰动系统[7]和时滞系统[8].事件触发切换系统是一种将切换、事件触发和网络传送等技术结合起来的一种新系统.文献[9]介绍了一种用于开关线性系统的事件触发取样和基于取样的稳态控制器.对于带有外扰的开关控制系统,文献[10]研究了基于观测器的事件触发抑制问题.在文献[11]中,针对时延时变的切换系统,研究了基于有限通信资源的动态输出反馈控制与周期事件触发机制.

事件触发判据的设计是控制系统性能的关键.良好的事件触发准则可以有效地减少通信,并能保持良好的闭环系统性能.迄今为止,研究者们已经提出了许多有效的触发条件,例如与状态有关的触发条件,输出相关的触发条件[12],以及周期性的触发机制[13]等.文献[14]提出一种动态触发机制,该机制能够根据目前的取样数据传送数目来自动调节,以达到节约网络资源的目的.文献[15]提出一种周期动态事件触发方案,并应用模态相关的平均驻留时间和多李雅普诺夫函数方法,得出切换系统指数稳定性条件和H∞性能.文献[16]通过混合动力学方法,将切换仿射系统周期时间触发控制拓展到事件触发控制.

但是,这些研究都没有考虑到模态信号在传输过程中会出现的时延,并且由于采用了通信网,会产生能量限制、量化误差和带宽限制.在网络开关系统中,由于外界的干扰会降低系统的运行效率,因此,在设计切换律时要考虑到能耗、Zeno行为和通信延迟等问题.所以,在存在外部影响的情形下,对具有通信时延的动态事件触发切换系统的研究有着很大的理论意义与价值.然而,关于受外源干扰的不确定切换系统事件触发控制问题的相关文献还较少.因此,本文将研究开关系统在动态周期事件触发机制下的切换律设计,指数稳定性及H∞性能分析问题.本文的主要工作总结如下:

1) 将DC-DC变换器建模为切换系统,针对该系统设计了良好的动态周期事件触发机制(DPETM),在更大程度上减少了通信资源浪费,避免触发Zeno行为,保证了良好的系统性能.

2) 将文献[17]的结果推广到了含有外源扰动及不确定因素的情况下.在动态周期事件触发条件下,利用线性矩阵不等式方法得到了保证扰动在期望水平上指数衰减的充分条件,给出了具有通信时延的切换控制系统的事件触发通信方案和H∞控制设计方法.

1 问题陈述

1.1 DC-DC升压变换器切换模型描述

图1为DC-DC升压变换器,Vin为输入电压,R为负载电阻,R0为电感等效内阻,iL为电感电流,uC为电容电压.根据开关S及二极管VD导通、关断情况,DC-DC升压变换器的输出控制是通过功率开关管的开与关在两个模态之间转换完成的.

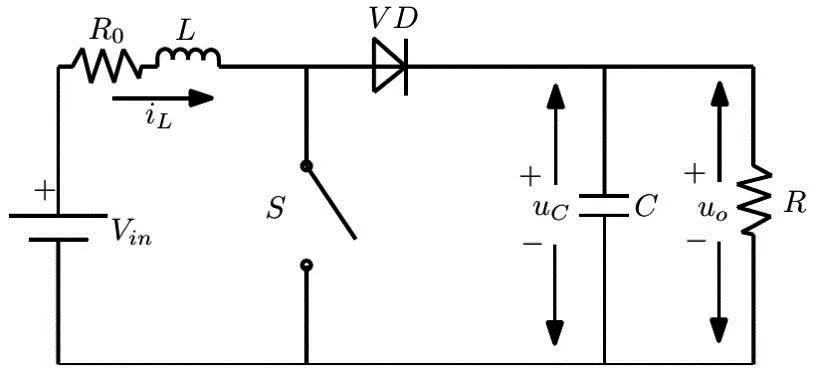
图1 DC-DC升压变换器系统框图

当开关S处于导通状态时,DC-DC升压变换器的模型为

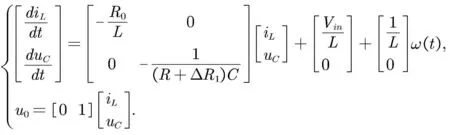
当开关S处于关断状态时,DC-DC升压变换器的模型为

其中ω(t)为输入电压的干扰,ΔR1,ΔR2分别为S导通和断开情况下负载电阻的扰动量.

对于上述模型中的不确定项R-ΔR展开为泰勒级数,忽略高次项,得到下式

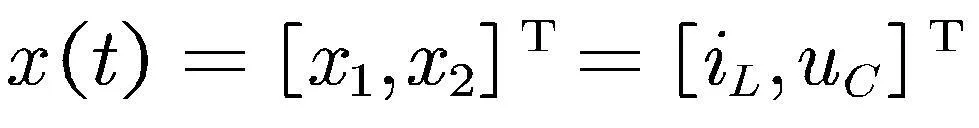
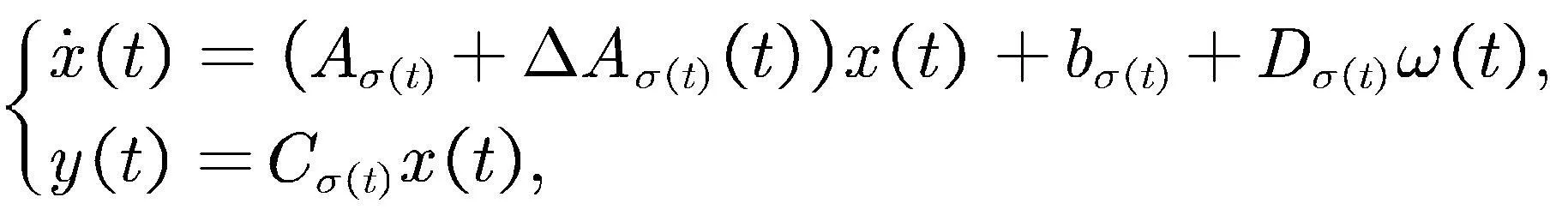
(1)

其中

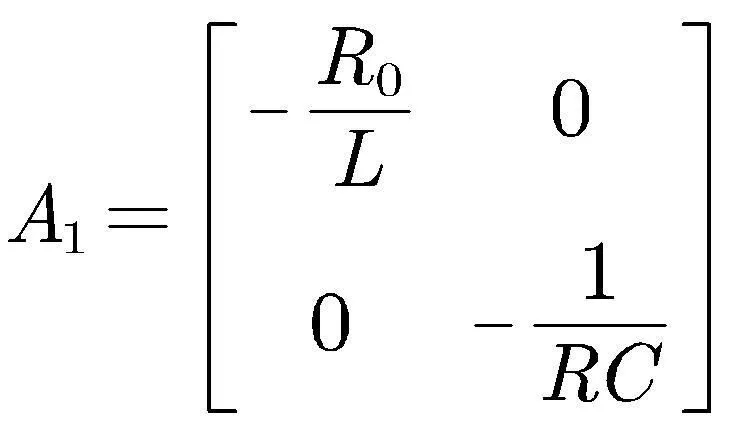
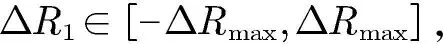
其中

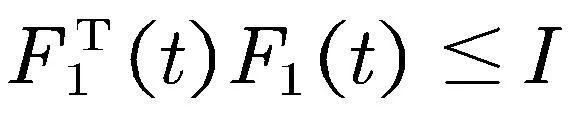
系统(1)是含有两个子系统的切换系统,状态维数为2.把该系统引入于更一般的情形下,令x(t)∈Rn,y(t)∈Rq分别是系统状态和系统输出.Aσ(t),Bσ(t)和Cσ(t),Dσ(t)为具有合适维数的实常数矩阵.σ(t):[0,∞)→SN={1,…,N}是表示系统切换信号的分段常函数,N则表示子系统的数量.接下来将针对一般形式的切换系统进行讨论.

1.2 动态周期事件触发机制设计

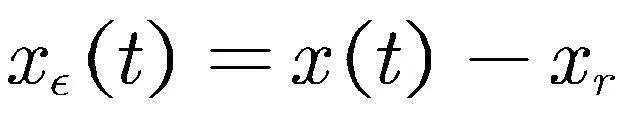
(2)

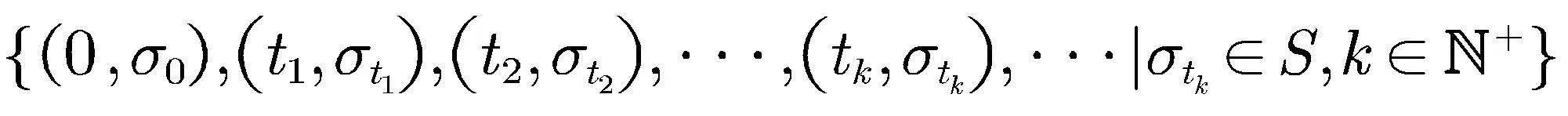
引入动态周期事件触发机制如下

(3)

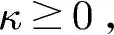
(4)

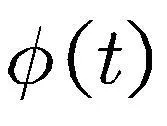
(5)

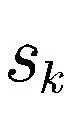
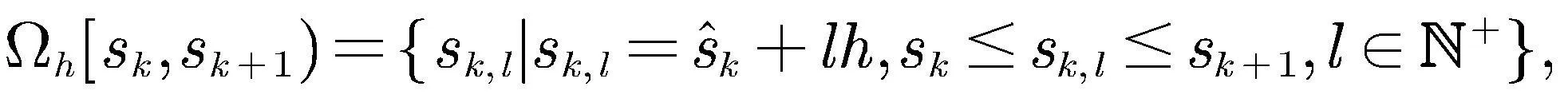
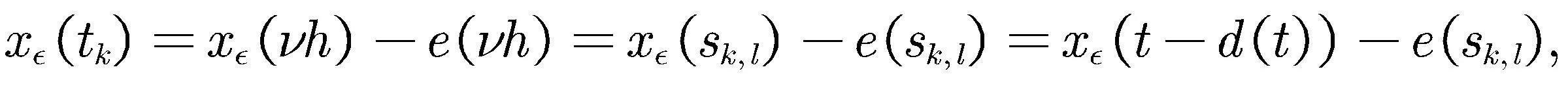
(6)

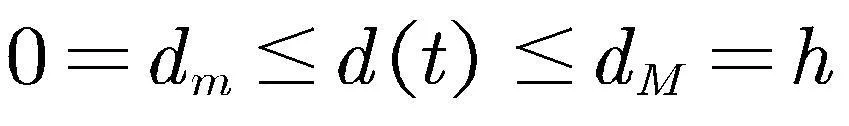
1.3 定义及引理

为了便于推导,在进行下一步的主要结果分析前,给出了以下有关的定义和引理.

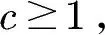
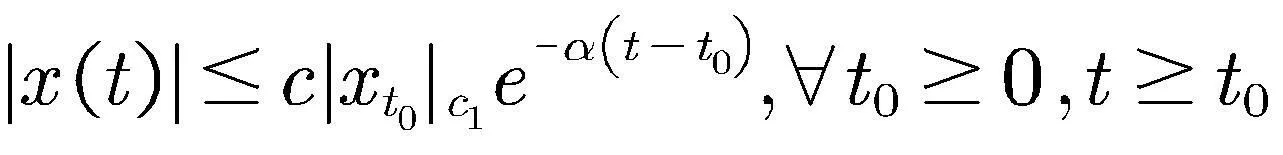
其中

,

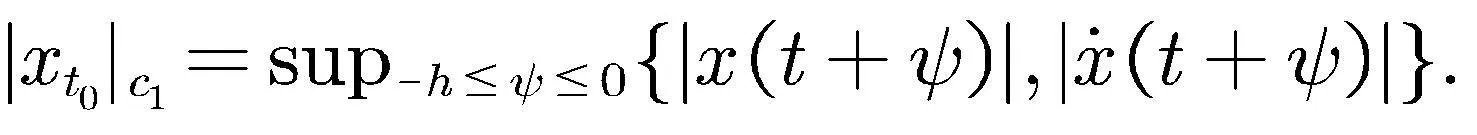
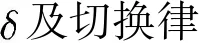
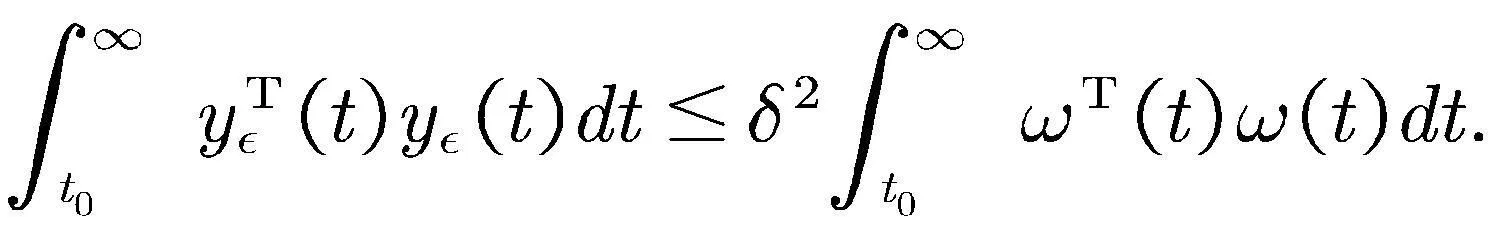
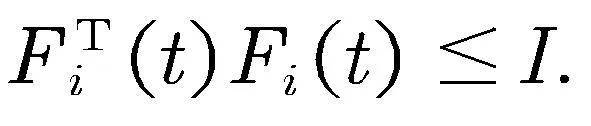
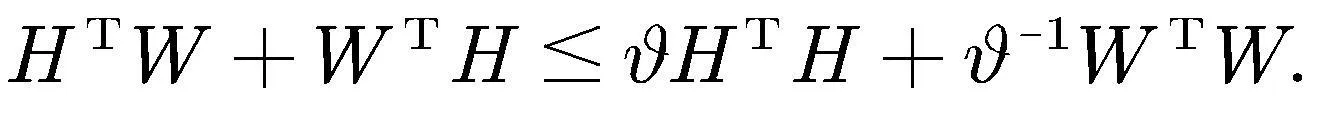
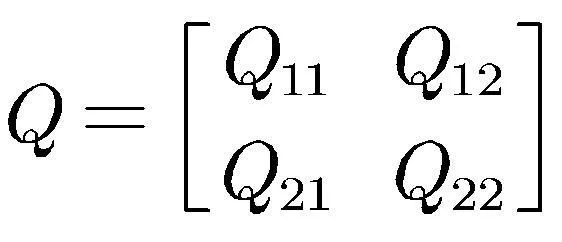
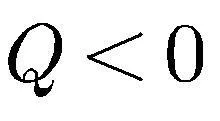
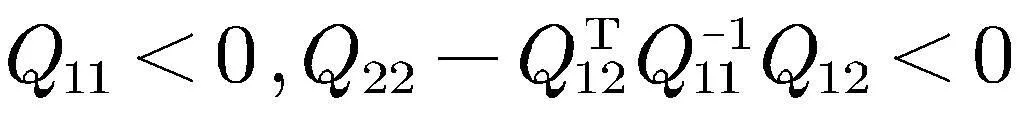
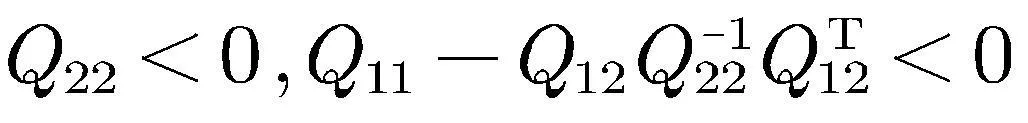
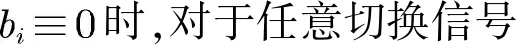
2 主要结果

这一部分主要研究了DPETM下系统的状态相关的控制律,并对系统H∞性能进行了分析.

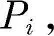
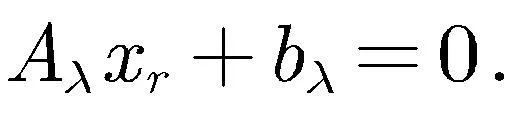
(8)

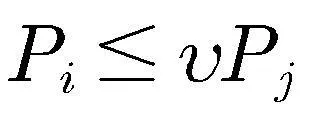
(9)

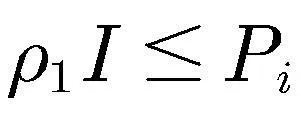
(10)

选取状态依赖的切换控制律如下

(11)

其中

,

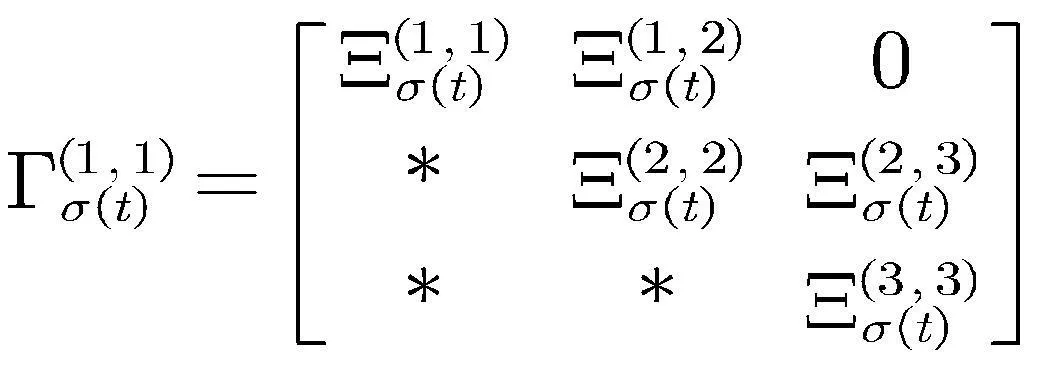
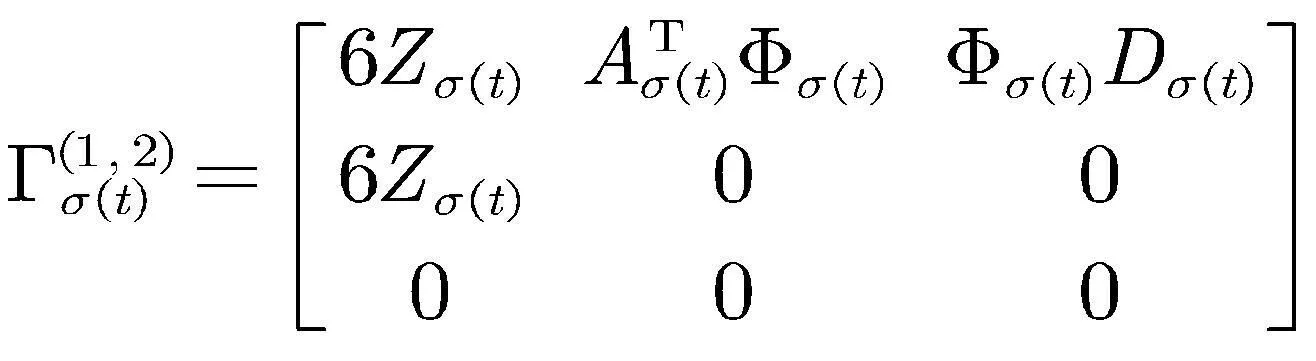
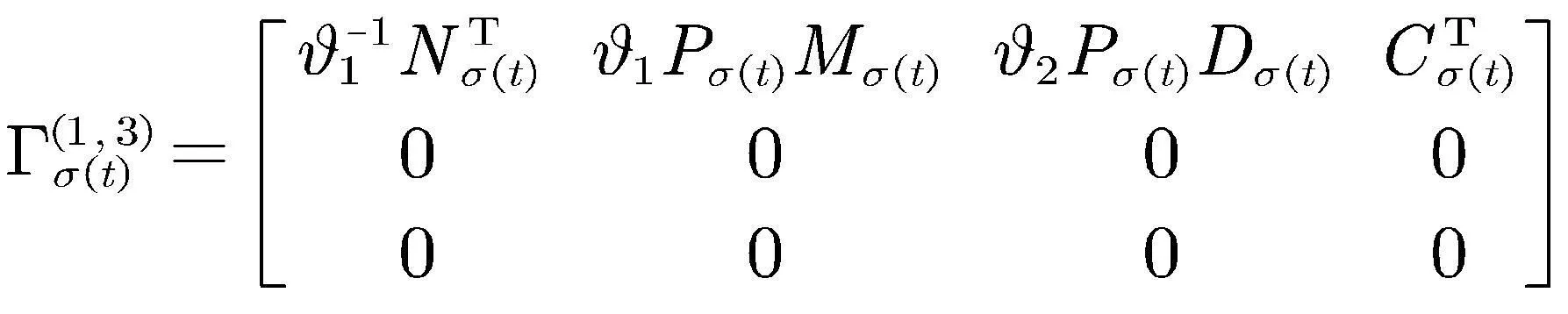
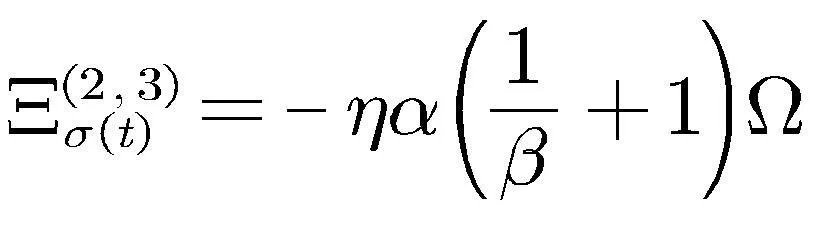
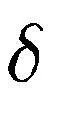
证明首先,构造一个如下形式的Lyapunov-Krasovskii 泛函

(12)

其中

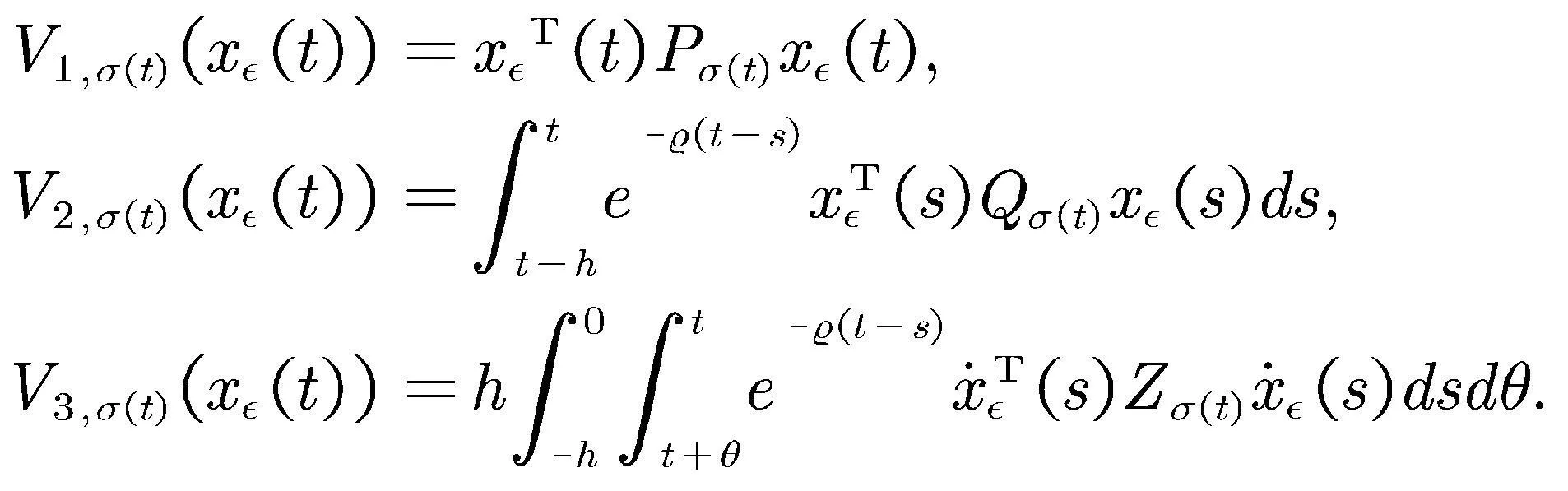
(13)

(14)

根据引理2和式(14)得

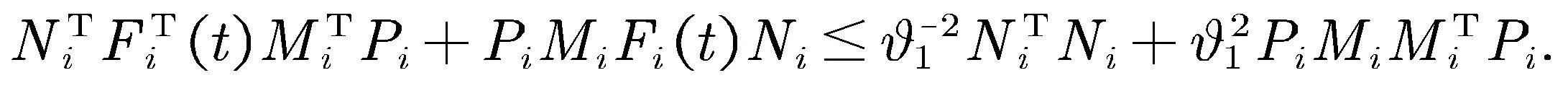
(15)

(16)

从式(12)～(16)的推导可得,在式(8)的条件下,Lyapunov-Krasovskii泛函的导数为

(17)

结合事件触发条件可将(3)重新描述为

(18)

(19)

(20)

根据引理5可得

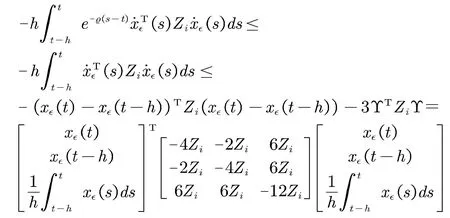
构造如下矩阵

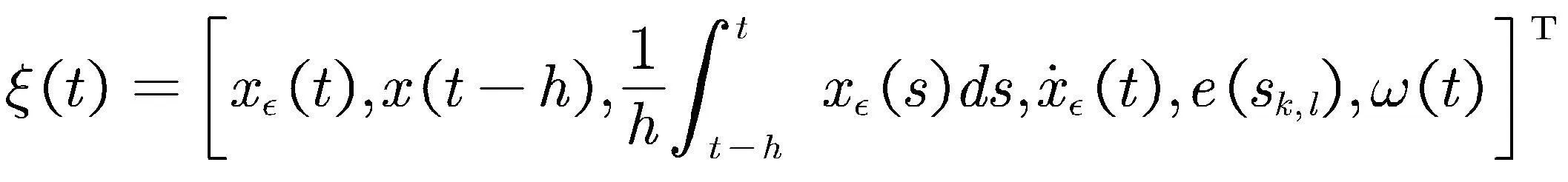
(23)

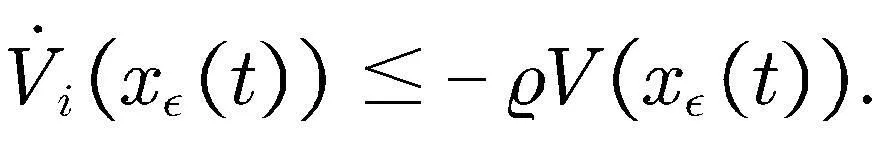
(24)

对式(24)积分,可推导出

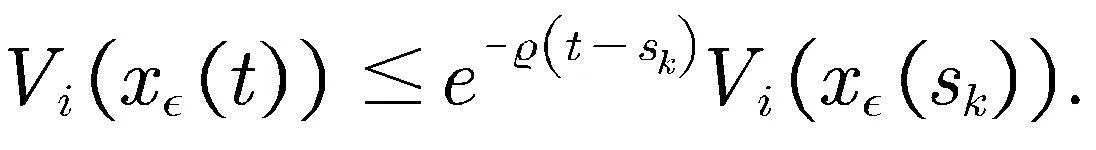
(25)

根据式(9),得

(26)

从式(24)～(26)及定义3有

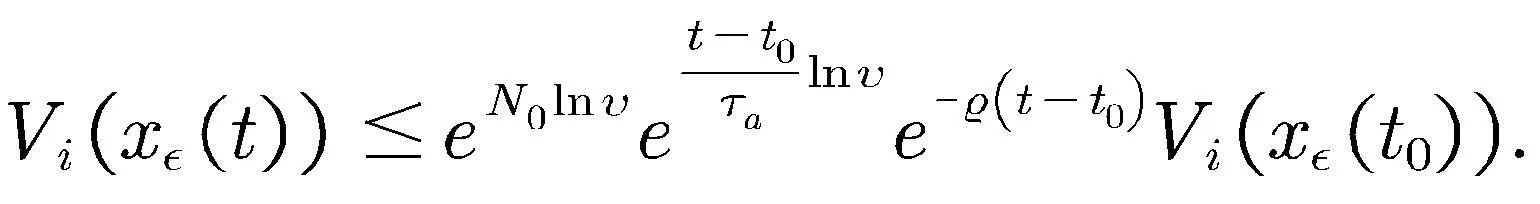
(27)

根据式(17)及(27)可得

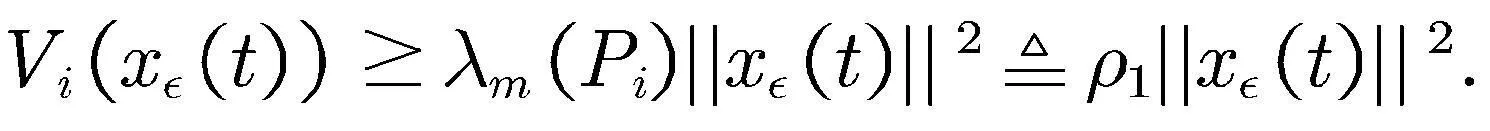
(28)

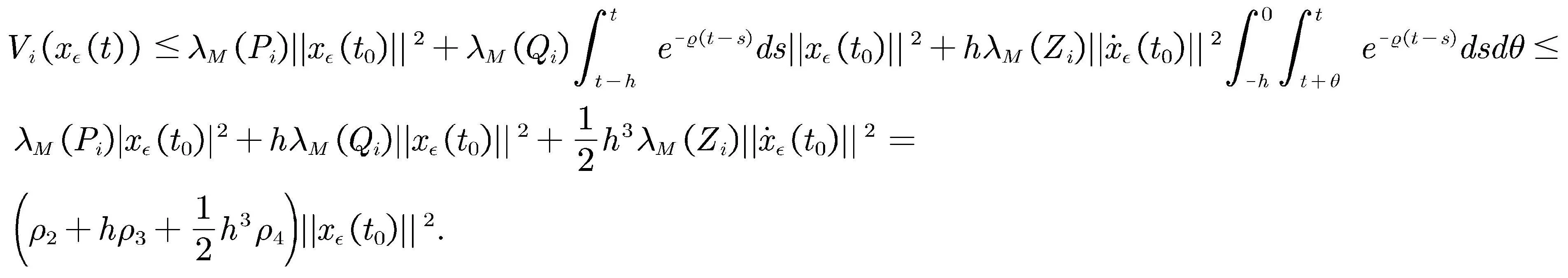
(29)

(30)

由定义1可得

(31)

其中

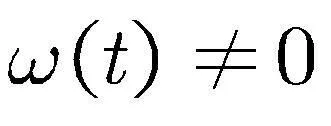
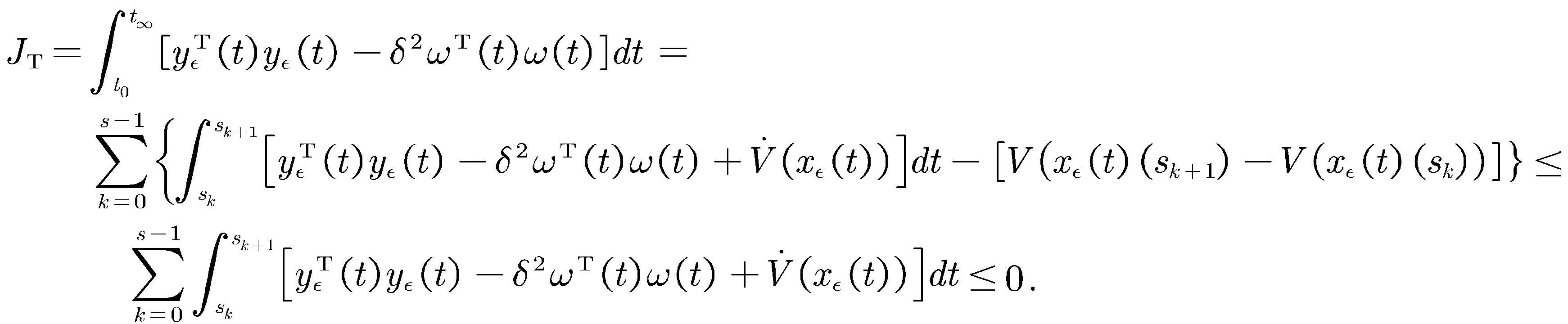
(32)

因此可得

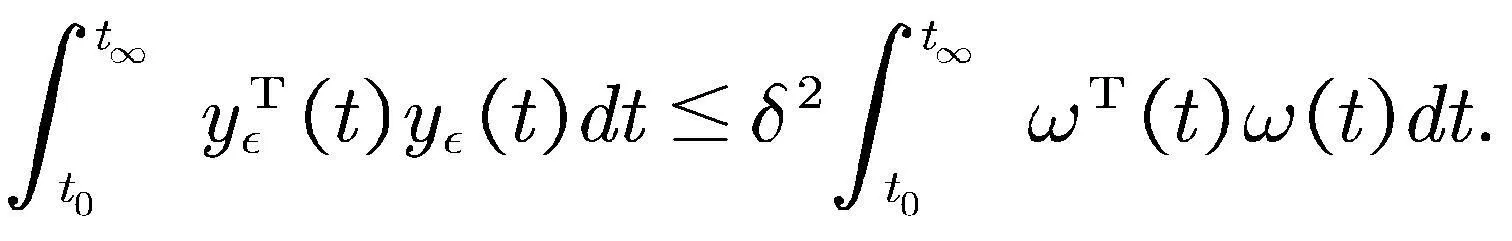
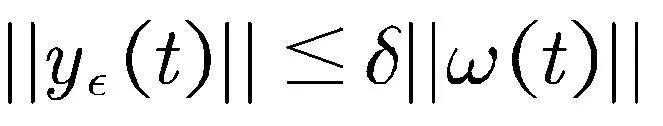
系统(2)的切换律可描述为

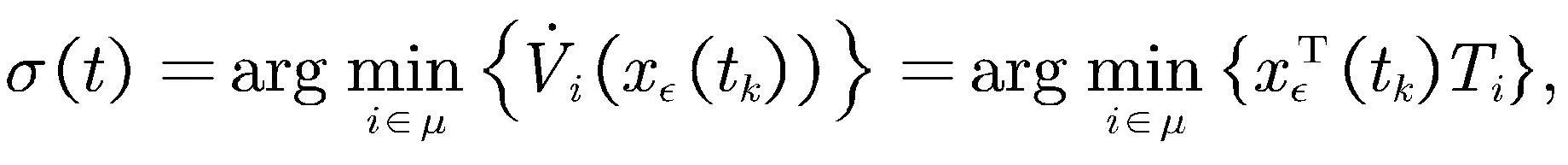
(33)

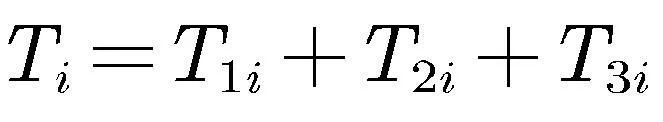
可得

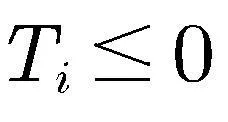
(34)

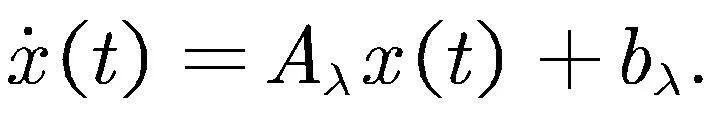
(35)

由式(8)可以推出切换平衡点的计算公式为

(36)

得到切换律表达式为

(37)

因此,系统在开关S处于导通状态和关断状态之间的切换关系为

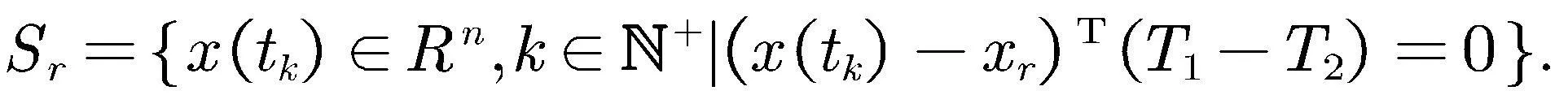
(38)

综上可知,系统(2)状态依赖的切换控制律为

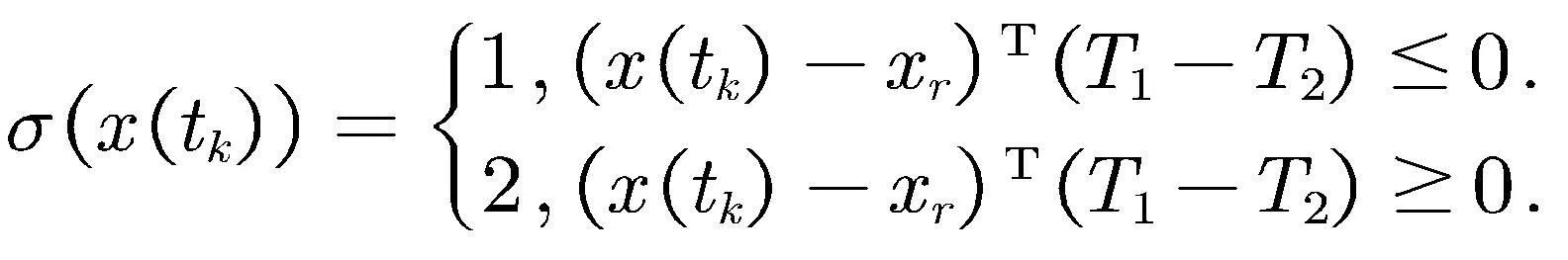
3 仿真实例

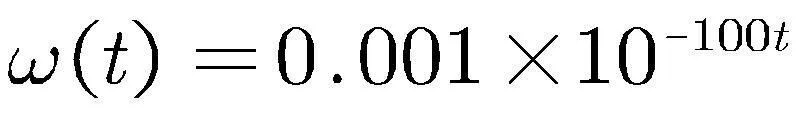
表1 DC-DC升压变换器仿真参数值

DC-DC升压变换器的两个工作模态分别如图2和图3所示.

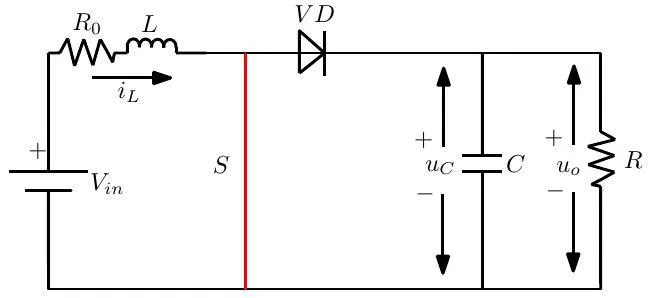
图2 工作模态1

图3 工作模态2

模态1:开关S导通,二极管VD关断

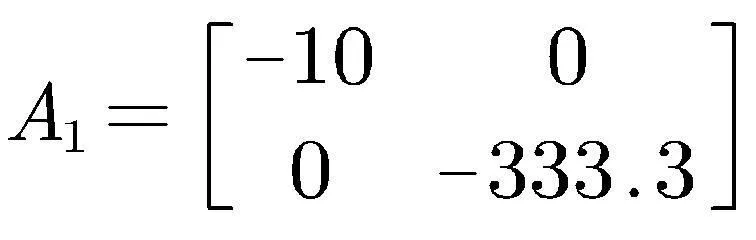
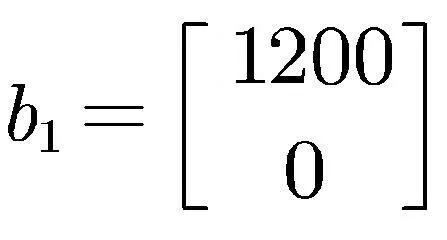
模态2:开关S关断,二极管VD导通

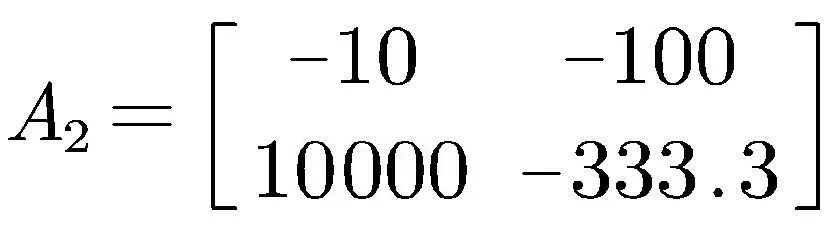
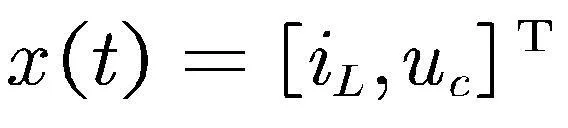
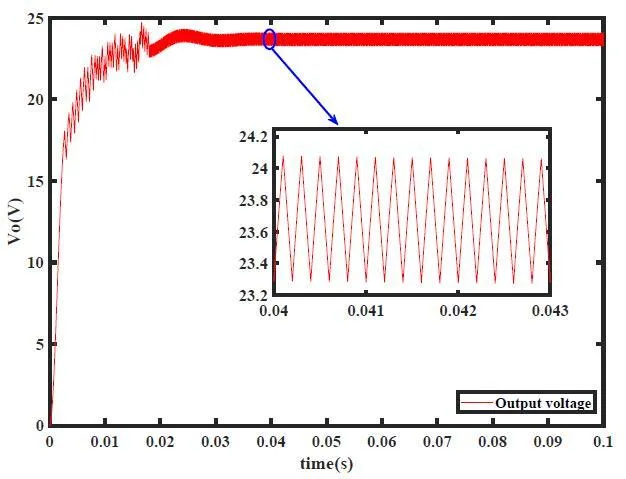
(a) 输出电压波形

控制参数η与β对DC-DC升压变换器系统性能的影响如图5所示.

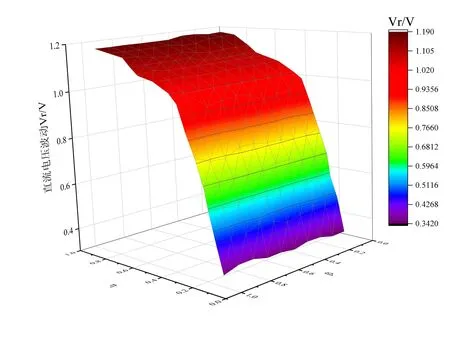
(a)直流电压波动

1)图5(a)为直流电压波动Vr.在DPETM下,Vr在[0.342,1.189 1]V范围内波动,触发参数η的改变能明显地影响输出电压值,但β对Vr的值不敏感,对系统性能影响较小.

2)图5(b)为电感电流波动Ir.在DPETM下,Ir在[0.023 1,0.104 4]A范围内波动,触发参数η在[0,1]内变化时,Ir的值逐渐增大,稳态运行时β对系统性能影响较小.

不同触发机制的系统性能对比见表2.当触发参数η=0.01时,2,3,4三种触发机制的系统性能相差较小,但相比于TTM策略,SETM,PETM和DPETM策略的触发次数明显更少.此外,与PETM略相比,DPETM策略能更有效地调节触发条件阈值,使得触发次数更少,从而减少通信负担并保证较好的系统性能.

表2 不同触发机制系统性能对比

4 结论

本文研究了在动态周期事件触发机制下,变换器控制律的设计.首先,利用不确定的参数和外界的扰动,建立了变换器开关系统的数学模型,并将其转化为误差跟踪系统.设计了引入动态变量的周期事件触发机制,对误差跟踪系统模型进行状态依赖的切换控制律设计,得到系统具有H∞性能指标的设计条件.最后,建立DC-DC升压变换器系统仿真模型,结果表明本文所设计的状态依赖切换控制律能够使得系统的输出电压,电感电流值跟踪到期望平衡点,且所设计的DPETM可以更有效的节约通信资源,证明了所设计的动态周期事件触发切换控制律的有效性.