基于属性分组的子空间聚类算法研究

庞 宁,靳黎忠

(太原科技大学应用科学学院,山西 太原 030024)

聚类分析是将数据集自动划为若干类簇的数据分析过程.高维属性空间的稀疏性使得全属性空间下距离度量失去意义,不同的类簇存在于不同的属性子空间上.因此,在聚类分析过程中,应考虑不同属性组(即属性子空间)对类簇形成作用的差异性.子空间聚类算法成为自动探索属性子集,以及提高高维数据聚类结果理解性的有效途径之一.

1 相关工作

1.1 高维数据聚类

子空间聚类是解决高维数据聚类分析的有效手段之一.作为最早被提出的子空间聚类算法,CLIQUE算法[1]是一种基于网格的子空间聚类,采用类Apriori方法,以自底向上的方式递归地寻找高密度子空间.ENCLUS算法[2]是在CLIQUE算法基础上提出的,ENCLUS算法采用熵值小于预定阈值方法,作为提取类簇子空间的准则.MAFIA算法[3]采用基于直方图的专门技术合并网格,可有效减少分区数量.但上述方法均采用基于网格的方法,导致严重依赖网格的位置.

由于使用降维技术,谱聚类也用于解决高维数据聚类问题.稀疏子空间聚类使用系数矩阵构造数据的相似度矩阵,再采用谱聚类形成最终结果[4].文献[5]通过在样本自表示框架中进行特征选择和子空间学习,以低维空间学习的亲和矩阵作为最终的聚类结果.上述基于谱聚类的聚类方法适合聚类类别较小且均衡分类的情况,对聚类参数的选择较敏感.

1.2 分类数据聚类算法

K-modes算法[6]及其各种改进算法是分类数据聚类分析的典型研究代表.fuzzy k-modes算法[7]利用模糊中心的概念解决分类数据类簇的不稳定性.COOLCAT算法[8]是一种基于熵的模糊聚类算法,该算法使用信息熵去度量类内属性值分布的差异性.在k-modes算法基础上,文献[9]为类簇的每维属性计算双权重值,并以此识别不同类簇的重要属性子空间.上述基于mode聚类方法的不足在于只能获取类簇中数据的部分信息.

针对高维分类数据聚类问题,硬子空间聚类使用0或1,表示属性子空间的权值,例如,SUBCAD算法[10]需要反复迭代更新属性权值,存在时间复杂度高等问题.软子空间聚类需给各类的属性赋予不同的权值,以度量不同属性对各类簇的聚类贡献程度,例如,PROCAD算法[11]利用属性值的出现频率度量其属性权值;文献 [9,12-13]提出的算法均是在K-modes的基础上扩展改进而来,各算法在优化权重计算上有所区别,但权重计算容易产生对属性重要性的偏差判断.

本文提出一种基于属性分组的软子空间聚类算法SSC,该算法采用属性分组技术将相关属性划分到同一组别中,根据组内属性间的相关性为各属性赋权值,构造不同属性子空间,以最大化簇集质量为聚类目标,在不同子空间上提取各自类簇.

2 问题描述

设DB是一个包含n个数据对象的分类数据集,可表示为DB={Oi| 1≤i≤n},其中,每个数据对象Oi有d维属性,Oi={aij| aij∈Aj,1≤j≤d},aij代表第i个数据对象在第j维属性上的取值,是一个分类数据值,Aj表示第j维属性.SSC算法需要解决的问题是:将数据集DB划分为若干类簇Ci,不同的类簇Ci对应不同的属性子集SAi,SAi⊂A,A是DB的属性集,本文所使用的主要符号详见表1.

表1 符号表示

3 基于属性分组的软子空间聚类算法

本文提出的基于属性分组软子空间聚类算法SSC由以下四个重要步骤组成,分别为属性分组、去除冗余属性、计算权重、软子空间聚类.

3.1 属性分组

挖掘具有强相关性的属性组,有利于区分不同属性在聚类过程中重要程度,从而搭建属性子空间.本文采用基于属性相关性的属性分组技术,将所有属性划分成若干组,组内的属性具有强相关性,属性分组的目的是找到彼此相关的属性,进而挖掘属性相关性对属性权值的影响.分析可知,组内属性的相关度越高,其对聚类的作用越大.借鉴文献[14]的方法,本文采用互信息和熵的比值计算属性Ai和属性Aj的相关度FR(Ai:Aj),可表示为公式(1).

(1)

其中,MI(Ai:Aj)和 H(Ai:Aj)分别指属性Ai和属性Aj之间的互信息和熵.FR(Ai:Aj)取值范围是[0,1],该值越大,则表示属性Ai和属性Aj之间的相关性越强.

由于属性子空间数量无法预先设定,同时,不同的属性子空间之间可能会有重叠,即,某些属性会出现在不同的子空间上,所以,不能采用传统的聚类方法进行属性分组.本文采用一种类似聚类的方法将相关性高的属性分到同一组内,所有属性都要参与每组的分配过程.只要符合分组条件,无论该属性是否已经归到某个属性组内,均可被再次分配到其他组内.具体属性分组算法如下:

算法1 属性分组算法 输入 分类属性集A={A1,A2…Ad},Ai是数据集DB上的第i维属性.输出 属性组AC={AC1,AC2…ACk},ACi是第i个属性组.Step1.随机选择一个属性,作为初始组AC1的初始属性,即AC={AC1}={{A1}}; Step2. for i=1 to |A| for m=1 to |AC|for j=1 to |ACm|if FR(Ai:Aj)<0.5 then {flag=false;continue;}endforif flag then ACm=ACm∪{Ai};endforif Ai没有被划分到任何属性组内then AC=AC∪{ACNEW}= AC∪{{Ai}};endfor Step3.重复step2 直到各属性组AC内的属性基本不变;

通过算法1,可形成若干属性组,组内属性高度相关.在高维数据聚类过程中,属性子空间上的属性彼此相关程度很高,往往更能预示出不同类簇的隐含信息.因此,基于属性相关技术划分出的属性组是构建属性子空间的关键环节.

3.2 去除冗余属性

在算法1所形成的属性组中,有一些属性组内只包含了一个属性,可认为这些属性与其他属性不相关或是冗余属性,需要被删除.识别并删除冗余属性的过程,见算法2:

算法2 去除冗余属性算法 输入 属性组AC={AC1,AC2…ACk}.输出 非冗余属性组集CAN.Step1.for i=1 to |AC| if |ACi|==1 then R=R∪{ACi};endfor Step2.CAN←AC-R;

3.3 计算权重

在高维数据聚类过程中,各属性的重要程度显然不同.属性之间相关度越高,说明彼此相互影响程度越深,聚类作用越大,其赋权比例应该越大.基于属性相关度的分组技术可以有效地将相似属性分为一组,属性权重值受到组内其他属性影响,同时,某些属性可能属于不同的属性组,因此,属性权重值的度量要综合考虑所有相关属性组,即,属性权重值应为其在各属性组内与其他属性相关度平均值的总和,可表示为:

(2)

其中,CRk是属性所属的第k个属性组,其值为属性Ai的组内所有相关属性Aj相关度FR(Ai:Aj)的平均值,m表示属性组CRk内属性数量.

计算各属性权重值是构建属性子空间的关键环节,软子空间聚类的价值在于所有属性均参与聚类过程,但参与度却决于其权重值.算法SSC计算属性权值的具体过程,见算法3:

3.4 子空间聚类

子空间聚类算法是将高维空间的数据映射到多个低维子空间上,并在低维空间上的聚类过程.在聚类过程中,聚类目标的设定与聚类准确性息息相关.本文的聚类目标为最大化类内数据之间相似度,最小化类间数据的相似度.采用多目标聚类质量函数在不同属性子空间上进行聚类,SSC算法的具体聚类目标可表示为多目标聚类函数Q(C),见公式(3).

(3)

其中, P(Cs)表示簇Cs在整个簇集C中的数量占比,代表了该簇在簇集中的重要程度,相当于整个表达式的权重值;C(Cs) 表示簇Cs的簇内紧凑程度;S(Cs)则表示簇Cs与其他簇的离散程度.

簇内紧凑度C(Cs)通过度量簇Cs内数据Oi的每个属性Aj上属性值aij概率值P(aij)与条件概率值P(aij|Cs),刻画了簇内紧凑度C(Cs),具体计算如公式(4)所示.

(4)

其中,P(aij)表示属性值aij在属性Aj上的出现频率,P(aij|Cs)表示在簇Cs内,属性值aij在属性Aj上的出现频率,W(Aj)表示属性Aj的权值.

簇间离散度S(Cs)取决于属性取值aij相对于簇Cs的专属程度,即属性Aj上的属性取值aij出现在簇Cs中的比例越大,说明该属性取值对于簇Cs与其他簇的离散作用越大,其数学形式表示如公式(5)所示.

(5)

其中,P(Cs|aij)表示在属性Aj上属性取值为aij的数据,在簇Cs中出现频率.

SSC算法在所构建的属性子空间的基础上,以最大化簇集质量为聚类目标,迭代调整各类簇内的数据分布.具体算法过程如下:

4 实验与分析

4.1 测试数据集与评价标准

4.1.1 测试数据集

本文使用UCI数据集和人工合成数据集对算法进行测试.UCI数据集与人工合成数据集内的属性值均为分类型数据.测试数据集具体情况详见表2,其中Voting、Mushroom和Splice均来自加州大学欧文分校用于机器学习的数据库(简称UCI);人工合成数据集包括:DB1、DB2和DB3.数据集DB1的属性总数为200维,主要用于测试属性数量的改变对于各算法运行时间的影响;数据集DB3的数据总数为40 000,可以用于评测各算法运行时间与数据点之间的关系.

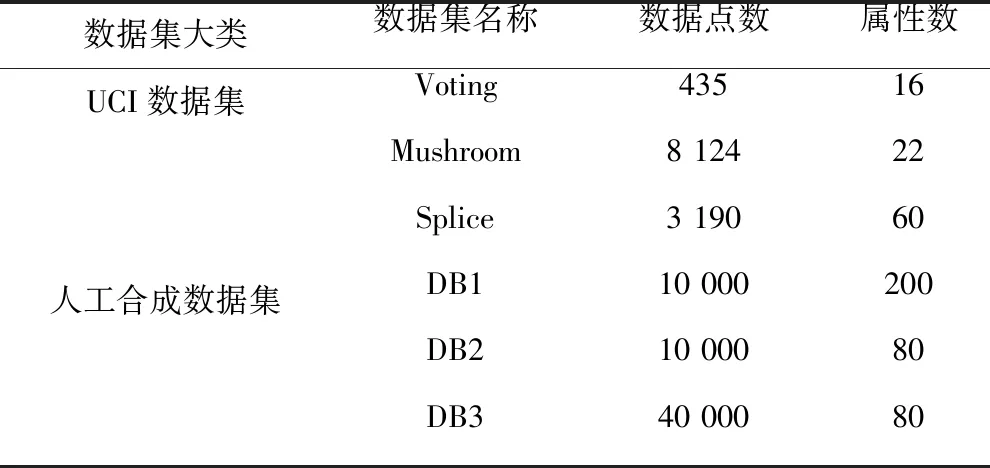
表2 测试数据集

4.1.2 评价标准

本文采用外部评价指标,调整兰德系数ARI、纯度Purity、雅克比系数Jaccard以及兰德系数RI,作为算法SSC与其他对比算法的评测依据.ARI主要测试聚类结果和真实类簇之间数据分布的吻合程度;Purity评测每个类簇中的主导数据占总数据的比例;Jaccard系数度量同类数据对在同一类簇中的占比;RI评测同类数据对被聚合以及异类数据对被分离的比例[15].

4.2 对比算法

本文选择子空间聚类算法PROCAD[11]、AT-DC[16]、DHCC[17]作为对比算法.这三种算法无须预先输入阈值并且都以分类数据作为分析对象.

PROCAD算法通过属性值在维度上的出现频率度量属性权重,聚类过程兼顾紧凑性和分离性的聚类目标.该算法将属性值作为度量属性权值的基本单元,有利于提高聚类精度,但也增加算法运行成本.AT-DC算法和DHCC算法均采用层次聚类,区别在于:前者以属性值在簇中的条件概率作为属性权重度量标准,使用两阶段聚类思想,实现划分最优解;后者采用多元对应分析思想描述各属性的聚类重要程度,使用分裂层次聚类思想构造类簇树状图.AT-DC算法和DHCC算法对于数据分布结构不敏感,有利于处理不同数据集,但却无法给出类簇相应的属性子空间.

5 实验结论

5.1 聚类性能对比实验

本实验主要测试算法SSC与其他对比算法在UCI数据集和人工合成数据集上的聚类效果,分别从聚类指标ARI、Purity、Jaccard以及RI四方面对比各算法在聚类性能上的差异并分析其原因.

5.1.1 UCI数据集上的对比实验

图1显示了算法SSC与其他对比算法在三个UCI数据集上的聚类性能差异,图1(a)、图1(b)、图1(c)和图1(d)分别从四个聚类评价指标上进行了聚类性能对比.从图1可见,算法SSC在数据集Voting和Splice上的聚类性能优于其他三种算法,尤其是,在数据集Splice上,算法SSC四个聚类指标的优势均非常明显,而算法PROCAD在数据集Mushroom上的聚类效果领先于其他算法.造成上述聚类性能差异的主要原因是:①算法PROCAD的属性权重赋值粒度小于算法SSC,给属性取值赋权重更有利于精确刻画属性子空间,尤其是类似数据集Mushroom,属性值域范围较大;②算法SSC使用属性分组技术,利用属性之间的强相关性度量属性权重值,强化了属性之间相互影响对聚类的作用,对于数据集Voting和Splice而言,属性取值在各属性上基本呈现均匀分布的特点,仅用属性出现频率无法有效区分聚类重要性,算法SSC可有效地解决该问题;③算法SSC通过迭代调整数据划分,直至类簇结构最优,追求簇内紧凑和簇间分离多目标的聚类效果,保证了类簇的整体聚类精度.

(a)ARI值对比

5.1.2 人工合成数据集上的对比实验

本文针对人工合成数据集分别测试了算法SSC与其他对比算法,图2显示了在人工合成数据集DB1、DB2和DB3上四种算法的ARI指标性能对比.观察实验结果可知:①算法SSC在三类人工合成数据集上的ARI指标值之间的差别不大,说明算法SSC对各种数据分布上的聚类性能很稳定;②算法SSC在三个合成数据集上的ARI指标值均优于其他三种算法,这一优势在数据集DB3上表现得尤为明显,在数据集DB1上四种算法之间的差异较小,主要原因是数据集DB3的属性空间重叠程度会造成属性赋权上的偏差,而数据集DB1相互独立的属性子空间和数据子集对各类子空间算法都很友好;③其他三种算法在各人工合成数据集上的聚类性能差异不明显,主要是由于该三种算法对数据分布不敏感造成的.

图2 各算法在人工合成数据集上的性能对比

5.2 算法效率对比实验

5.2.1 数据量上的可扩展性实验

图3显示了随着数据集DB3数据量的增加,算法SSC与三种对比算法运行时间的变化趋势,从图可知,四种算法均基本呈现线性增长.其中,算法PROCAD增速最为明显,DHCC在所有算法中的时间消耗最小,算法SSC的表现位于算法DHCC和算法AT-DC之间.主要原因是算法PROCAD的主要时间成本集中在属性取值赋权的计算过程上,显然,相比以整个属性为权重计算单位的方法,这种计算方式更为耗费时间,这一结论在维度的可扩展性实验上同样得到验证(见图4).

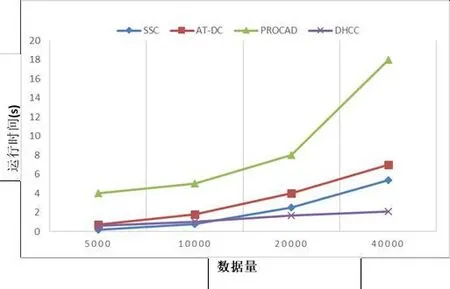
图3 数据量上的可扩展性实验

5.2.2 维度上的可扩展性实验

图4表明了随着数据集DB1属性的增加,四种算法在运行时间上的差异.算法DHCC的维度可扩展性最优,而算法PROCAD是四种算法中受维度增长影响最大的.在数据量扩展性能对比实验中,算法SSC仅比算法DHCC的表现略差,而在维度可扩展性上,算法SSC仅优于算法PROCAD,分析原因可知,算法SSC利用属性分组技术对所有属性的相关性进行分析计算,同时,利用多属性组之间的相互作用评价属性权重,这样的度量方式会受到属性数量的影响,当属性量递增时,算法在权重计算上所花费的时间也随之增加,特别是,当属性量大,属性之间的相互关系逐渐复杂时,这种时间成本增加的趋势也越加明显.

6 结论与展望

为了解决高维分类数据的聚类问题,本文提出一种基于属性分组的子空间聚类算法SSC,该算法利用属性之间的相关性,度量不同属性聚类重要度的差异,以多目标聚类质量最大化为目标,通过多次迭代,实现最佳的类簇划分.在人工合成数据集以及UCI数据集上,实验证明该算法具有正确性、有效性和良好的可扩展性.

本文下一步的研究方向将细化权重计算度量粒度,以属性取值为度量单位,而非整个属性;升级冗余属性的判断依据,在属性成组之前去除冗余属性的干扰;设计并实现算法并行化以适应海量数据的聚类需求.