落实新课标对尺规作图的新要求

李卓 代紫涵

【摘  要】  2022年教育部公布了新课标，与旧课标相比，新课标对尺规作图的要求发生了变化，因此相应地在修订初中数学教材时，也要对相关内容做适当的调整与修订.目前初中数学教材正在修订，笔者以人教版初中数学教材中与新课标尺规作图相关内容为例，对照新课标，结合自身研读课标、研读教材的体会，提出了初中数学教材中新课标尺规作图相关内容修订的若干思考.

【关键词】  新课标；尺规作图；初中数学教材修订；思考

2011年，教育部颁布了《义务教育数学课程标准（2011年版）》.2019年，教育部启动了对《义務教育数学课程标准（2011年版）》（以下简称旧课标）的修订.2022年，教育部公布了《义务教育数学课程标准（2022年版）》（以下简称新课标）.目前初中数学教材正在修订，笔者以人教版初中数学教材中与新课标尺规作图相关内容为例，对照新课标，结合自身研读新课标、教材的体会，谈谈初中数学教材修订的若干思考.

1  新旧课标对尺规作图要求的变化及意义

在图形与几何领域，与旧课标相比，新课标突出的变化是强化了几何直观的要求，扩充了尺规作图的内容［1］.旧课标将尺规作图置于点线面角、相交线与平行线、三角形、四边形、圆等基本几何概念之后，受到旧课标中尺规作图后置的影响，初中数学教材中有关尺规作图的内容也出现较晚.因此，尺规作图成为了一种学习任务，其在帮助学生理解几何概念与实际操作等方面的功能被大大削弱，影响了早期的直观运用［2］.新课标则采取“化整为零”的方法，将尺规作图植入到线点面角、相交线与平行线、三角形、四边形、圆等具体的内容中，而且新课标将尺规作图前置，小学阶段就加入了尺规作图的内容.初中阶段也加强了对尺规作图的要求，目的是帮助学生通过具体的操作活动，经历几何对象的图形构造过程，理解图形的组成元素关系与结构，培养几何直观［3］.

总的来说，新课标将尺规作图前置，增加了尺规作图的内容，对几何直观的要求明显提高，有利于帮助学生感悟图形的抽象存在，通过感知操作获得对事物的直观理解和判断［1］32.

2  对新课标规定尺规作图内容修订的思考

课程标准是教材编写的依据，新旧课标对尺规作图的要求发生了变化，因此相应地在修订初中数学教材时，也要对新旧课标对尺规作图要求有变化的内容做适当的调整与修订.

2.1  对初中数学教材中三角形两边之和大于第三边修订的思考

关于三角形两边之和大于第三边，旧课标在第三学段（7—9年级）规定：“证明三角形的任意两边之和大于第三边.”［4］新课标在第三学段（5—6年级）规定：“图形的认识教学要引导学生经历基于给定线段用直尺和圆规画三角形的过程，探索三角形任意两边之和大于第三边（例32），并说出其中的道理，经历根据两点间线段最短的基本事实说明三角形三边关系的过程，形成推理意识.”［5］

目前，人教版初中数学教材是先给出了一个探究活动：

“任意画一个△ABC，从点B出发，沿三角形的边到点C，有几条线路可以选择？各条线路的长有什么关系？能证明你的结论吗？”在构造出不同路线后，利用“两点之间，线段最短”这一基本事实构造不等式，从而得到“三角形两边之和大于第三边”这一结论，然后通过将不等式移项得到“三角形两边之差小于第三边”这一结论.

对照新课标，下一步修订初中数学教材中的三角形两边之和大于第三边时首先应将这部分内容前移到小学5—6年级，其次参考新课标中的例32，设置尺规作图探究活动，在活动中引导学生猜想出当两线段之和小于第三线段长时，这三条线段不能构三角形，进而可以得到猜想：三角形的两边之和大于第三边（鲍建生、章建跃在《数学核心素养在初中阶段的主要表现之三：几何直观》一文中也指出可以设计类似的探究活动），然后利用“两点之间，线段最短”这一基本事实证明三角形两边之和大于第三边.

2.2  对初中数学教材中平行线修订的思考

关于平行线，旧课标规定：“能用三角尺和直尺过已知直线外一点画这条直线的平行线.”［4］32新课标则规定：“能用三角板和直尺过直线外一点画这条直线的平行线；能用尺规作图：过直线外一点作这条直线的平行线.”［5］65

目前人教版初中数学教材在七年级下册平行线这一节中，在小节末尾的练习中提到：“读下列语句，并画出图形：（1）点P是直线AB外一点，直线CD经过点P，且与直线AB平行；（2）直线AB，CD是相交直线，点P是直线AB，CD外一点，直线EF经过点P且与直线AB平行，与直线CD相交于点E.”可以看到教材对于“过直线外一点作这条直线的平行线”这一作图活动并未提到尺规作图.

对照新课标，下一步初中数学教材修订时可以在“同位角相等，两直线平行”这一平行线的判定方法之后增加利用这一判定方法作“过直线外一点作这条直线的平行线”的尺规作图活动.

2.3  对初中数学教材中三角形全等判定修订的思考

关于三角形全等判定，旧课标规定：“掌握基本事实：两边及其夹角分别相等的两个三角形全等，两角及其夹边分别相等的两个三角形全等，三边分别相等的两个三角形全等.”［4］33新课标规定：“能用尺规作图：已知三边、两边及其夹角、两角及其夹边作三角形.”［5］66义务教育数学课程标准修订组组长东北师范大学校长史宁中教授也指出，还可以通过尺规作图，在充分感悟的基础上，猜想三角形全等的条件［6］26.

目前人教版初中数学教材中三角形全等的“SSS”“SAS”“ASA”这三种判定方法都是通过探究活动：先任意画出一个三角形，再画出一个，使画出的三角形与已知三角形三边分别相等或者两边和它们的夹角分别相等或者两角和它们的夹边分别相等，然后判断两个三角形是否全等，最后再以基本事实的形式给出“SSS”“SAS”“ASA”这三种判定方法.

对照新课标，下一步初中数学教材中三角形全等的“SSS”“SAS”“ASA”这三种判定方法的探究活动修订时首先明确是用尺规作图作出三角形，然后判断两个三角形是否全等.先任意画出一个三角形，再利用尺规作图作出一个与已知三角形三边分别相等或者两边和它们的夹角分别相等或者两角和它们的夹边分别相等的三角形，然后判断两个三角形是否全等，最后再以基本事实的形式给出“SSS”“SAS”“ASA”这三种判定方法.

对于“SSA”不能作为两个三角形全等的判定方法，教材则是通过“拼摆木棍”的实验：把一长一短的两根木棍的一端固定在一起，摆出△ABC.固定住长木棍，转动短木棍，得到△ABD.这个实验说明了什么？说明有两边和其中一边的对角分别相等的两个三角形不一定全等.

对照新课标，下一步初中数学教材修订时可以将教材中利用“拼摆木棍”探究三角形全等的“SSA”判定方法替换为利用尺规作图探究三角形全等的“SSA”判定方法，先任意画出一个三角形△ABC，再利用尺规作图作出与△ABC的两边和其中一边的对角分别相等的三角形，然后判断两个三角形是否全等.调整了之后既落实了新课标中尺规作图的理念，同时还可以通过探究“满足SSA的两个三角形是否有全等的情况”，“如果条件中的角换成直角，即如果一个直角三角形的斜边和直角边与另一个直角三角形的斜边和直角边分别相等，那么两个三角形一定全等吗？”很自然地引出直角三角形全等判定的HL定理.

2.4  对初中数学教材中圆的切线修订的思考

旧课标没有规定“过圆外一点作圆的切线”.与旧课标相比，新课标新增“过圆外一点作圆的切线（例76）”.目前人教版初中数学教材圆的切线章节中没有用尺规作图过圆外一点作圆的切线的相关内容，因此在下一步的教材修订中可以在圆的切线章节增加用尺规作图过圆外一点作圆的切线的相关内容.3  对新课标未规定尺规作图内容修订的思考

考虑到新课标非常强调尺规作图，笔者认为尽管有些内容新课标没有规定用尺规作图，但是在修订初中数学教材时仍然可以通过改编教材中的习题、新增尺规作图习题等方式融入尺规作图的理念.

3.1  改编初中数学教材中的习题

在修订初中数学教材时，可以通过改编初中数学教材中习题的方式融入尺规作图的理念.例如目前人教版初中数学教材在九年级上册圆周角这一节练习中有一个用三角尺找圆心的习题：“你能用三角尺确定一张圆形纸片的圆心吗？有几种方法？”在修订初中数学教材时可以将利用三角尺找圆心改为利用直尺和圆规找圆心.

再如目前人教版初中数学教材在八年级上册角的平分线的性质这一节复习题中也有一个用三角尺找圆心的习题：“为了促进当地旅游发展，某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等，应在何处修建？”在修订初中数学教材时可以在原问题后面增加一个问题：“请你用直尺和圆规找到修建度假村的点.”

3.2  新增尺规作图习题

除了改编教材中的习题，还可以通过新增一些尺规作图的习题.例如前文指出下一步的教材修訂中可以在圆的切线章节增加用尺规作图“过圆外一点作圆的切线”的相关内容，类似地也可以在圆的切线章节增加已知圆的切线，让学生用尺规作图作圆的习题［7］.

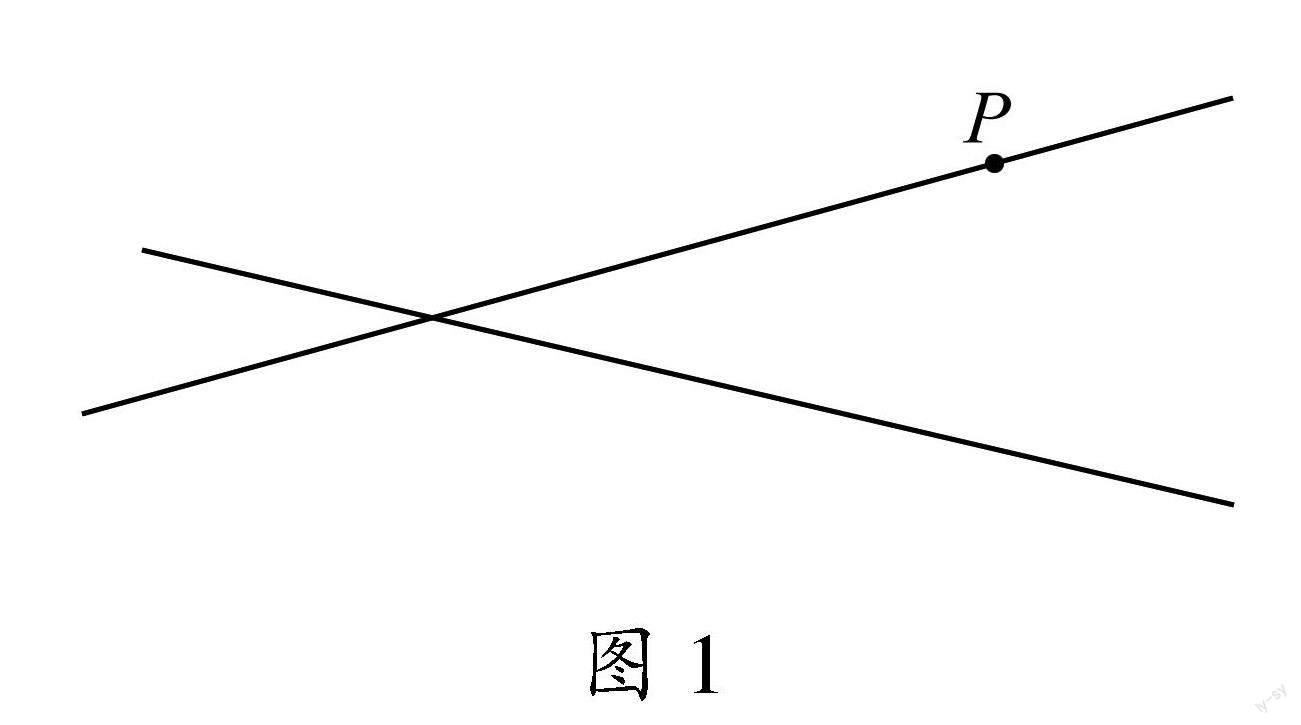
如图1所示，给定两条直线和一个点P，如何利用直尺和圆规作出与两直线相切的圆，并使P为切点之一.

再如可以增加让学生综合运用所学过的知识进行尺规作图的问题.以下是改编自中国台湾地区2012年初中生基本学力测验试卷的一个问题，要解决这个问题，既要用到圆的切线的相关知识，又要用到角平分线的相关知识，还要用到“过直线上一点作垂线”的知识［8］.如图2所示，AB为圆O的直径，在圆O上取异于A，B的一点C，并连接BC，AC.若想在AB上取一点P，使得P与直线BC的距离等于AP长，请你用直尺和圆规找到点P.

此外，新课标规定：“在尺规作图中，学生应了解作图的原理，保留作图的痕迹，不要求写出作法.”［5］根据新课标，或许还可以考虑增加给出尺规作图的方法和痕迹，让学生说出作图原理的习题.图3是来自中国台湾地区翰林版教材初二下册给出了尺规作图的痕迹和作法，让学生说出作图原理的一个习题.图34  结束语

建设一套“完美”的数学教材，不仅是编者的追求，更是一线教师的愿望［9］.考虑到与旧课标相比，新课标对尺规作图的要求发生了变化，笔者对初中数学教材中尺规作图相关内容提出了修订的建议.当然以上的一些想法只是自己的一孔之见，提出的修订建议也不完整，我们权当是抛砖引玉，不当之处，敬请同行批评指正.

参考文献［1］吴立宝，刘颖超，郭衎．2022年版和2011年版义务教育数学课程标准比较研究［J］.教育研究与评论，2022（05）：32.

［2］何煜晶，周超．日本初中教科书尺规作图编排及启示［J］.中学数学月刊，2022（02）：56.

［3］鲍建生，章建跃．数学核心素养在初中阶段的主要表现之三：几何直观［J］.中国数学教育，2022（Z3）：7.

［4］中华人民共和国教育部．义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012：33.

［5］中华人民共和国教育部．义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022：35.

［6］史宁中．数学课程标准修订与核心素养［J］.教育研究与评论，2022（05）：26.

［7］Schoenfeld，A.H.Explorations of Students’ Mathematical Beliefs and Behavior.Journal for Research in Mathematics Education，1989，20（04）：339.

［8］李建霖．尺规作图的任务分析与阅读理解层次［D］.台北：台湾师范大学，2014：2.

［9］印冬建．人教版“相似三角形的判定”（第一课时）修订建议［J］.中学数学杂志，2018（12）：18.

作者简介  李卓（1988—），男，山东曲阜人，博士，讲师，硕士生导师；主要从事数学教育研究.

代紫涵（1999—），女，湖北宜昌人，硕士研究生；主要从事数学教育研究.21世纪以来我国中小学数学变式教学研究的回顾与展望基金项目  2019年度国家社会科学基金项目“德育内容视阈下我国中小学理科课程的百年嬗变研究”（19BKS175）.