含缺陷变刚度层合板屈曲性能的数值分析方法

黄艳，王喆，陈普会，*

1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016

2.北京航空航天大学 航空科学与工程学院，北京 100083

3.中国飞机强度研究所 强度与结构完整性全国重点实验室，西安 710065

传统复合材料层合板采用直线铺层，限制了结构的设计空间，为进一步增强层合板的可设计性并提高结构效率，研究者提出了变刚度设计的概念，即改变层合板的刚度以满足不同结构的承载需求。目前通常采用改变纤维铺放角度的方式设计变刚度层合板［1］，能有效提高层合板的屈曲承载能力。

随着自动铺丝技术（AFP）的发展，通过纤维转向功能可改变丝束铺放角度，从而实现变刚度层合板的制造，同时该技术能单独控制每根丝束的切断与重送，调整丝束带在不同位置的宽度。作为一种低成本、高效率的自动化制造技术，可满足大曲率复杂构件的制造要求［2］。相比于常规层合板，变刚度层合板在制造过程中更易产生缺陷［3］。其中，由于曲率半径过小引起的纤维褶皱等缺陷可通过增大曲率半径或调整工艺参数［4］等方式达到减少或规避的效果，但由于丝束带宽度、切割方向及满铺覆性要求导致的丝束间隙与重叠等缺陷则无法避免［5-6］，仅能通过改变制造参数（如丝束宽度）、调整铺放角度等方式减少缺陷的产生［7-8］，因此有必要研究间隙与重叠缺陷对变刚度层合板屈曲性能的影响。

含缺陷层合板的研究首先需对缺陷进行位置确定与类型判断，目前已有研究人员对采用几种常用轨迹铺放的层合板进行了缺陷定位研究。Jegley 等［9］开发了计算网格中心处纤维方向的算法，该算法在相邻丝束带重叠处得到两个角度，以此获得含重叠缺陷层合板的厚度分布。但该方法需根据方程解的个数判断丝束带重叠情况并选取合适的解作为含缺陷单元的纤维角度，计算效率较低。此后Blom 等［10］利用丝束带特性导出了含间隙缺陷的等曲率铺放层合板中任意位置的间隙判断方程，杨竣博［11］结合Steffensen 迭代法提出了含重叠缺陷层合板的缺陷判断方法，钱金源等［12］则提出了不同铺放策略下采用Bezier 曲线铺放层合板的缺陷定位方法。以上3 种方法仅能通过反复求解位置方程实现单元中心点处缺陷类型的判断，构建的有限元模型的缺陷分布取决于网格尺寸，当网格尺寸偏大时可能导致无法识别分布于单元四周的缺陷或识别的缺陷单元实际缺陷占比很小，从而偏离实际的缺陷分布情况。

在缺陷定位与类型判断的基础上，研究人员采用不同的缺陷等效方式对含缺陷的变刚度层合板进行了有限元分析。Wu 等［13］通过增加壳单元厚度定义重叠区域网格的单元性能，Blom等［10］直接赋予间隙单元树脂性能，居相文等［14］也采用相同的方法分析了不同铺设策略下的层合板性能。然而当网格尺寸偏大时，实际网格范围内可能存在部分无缺陷区域，上述方法均不做区分地对其赋予完全间隙或完全重叠的材料属性，这将导致计算结果与实际结构的屈曲性能出现较大偏差。在此基础上，Fayazbakhsh 等［15］在缺陷修正模型中引入了间隙百分比，提出了用于分析含缺陷层合板性能的缺陷层法，Arranz［16］与Carvalho［17］等则对含间隙缺陷的材料性能进行了预测，是现有常规壳模型下较为精细的缺陷等效方法，降低了屈曲性能预测精度对网格尺寸的依赖性。不同于采用壳单元建模的方法，Falcó等［18-19］采用精细的网格直接建立了丝束带间的间隙区域，完全区分了缺陷材料与无缺陷材料，是目前最接近实际缺陷分布的方法。虽然这种方法建立的模型不再需要进行缺陷的性能等效，对于屈曲性能的预测更为精确，但需单独构建每一铺层中丝束带与间隙的精准模型，极大地增加了计算成本，很难用于后续层合板屈曲性能的优化分析。同时该方法无法建立含重叠缺陷的变刚度层合板模型。此外卫宇璇等［20］采用实体单元建立了含重叠缺陷的变刚度层合板模型，重叠区域采用两倍的单元厚度，导致铺层表面存在凸起，当相邻铺层角度不同时严重破坏铺层连续性，因此该方法通常仅限于采用重复铺层设计的层合板。类似地，Cao 等［21］采用两倍单元厚度表征重叠缺陷，并删去了位于间隙缺陷的单元，该方法存在不连续问题的同时低估了间隙区域对层合板性能的影响。

综合学者们的研究可发现目前采用的方法主要通过考虑纤维轨迹特性、铺放方式与丝束宽度等因素进行公式推导并利用脚本文件判断缺陷位置及类型。在后续的有限元分析中，该方法可以判断模型单元中心点是否有缺陷，并将单元分为缺陷单元和无缺陷单元。然而实际层合板结构在不同位置的间隙缺陷程度与重叠缺陷程度往往不同，将缺陷程度较低的单元直接划分为缺陷单元会导致预测结果过于保守（间隙缺陷）或高估层合板性能（重叠缺陷）。此外，该定位方式建立的等效模型预测精度很大程度上取决于模型的单元尺寸。因此含缺陷层合板等效模型的建立与分析还需进一步研究。

间隙与重叠缺陷在变刚度层合板中的分布主要由丝束带宽度、纤维曲线路径定义方式、铺层覆盖策略、丝束覆盖比例等因素决定，充分研究缺陷的形成机理是预测含缺陷层合板屈曲性能的前提。本文详细分析了制造过程中间隙与重叠缺陷的形成机理，并在此基础上提出了预测变刚度层合板缺陷分布的方法。采用缺陷占比表征局部区域中材料含缺陷的程度，基于代表性体积单元（RVE）提出了含缺陷材料的简化模型，建立了含缺陷材料性能的计算方法。同时利用二值图像法识别并构建有限元模型中含不同缺陷占比的单元集合，结合提出的性能计算方法赋予不同集合的单元不同的材料性能。最终通过该有限元模型计算含缺陷层合板的屈曲性能，并与试验进行对比，以期验证方法的有效性。

1 变刚度层合板缺陷形成机理及分布

1.1 纤维曲线路径定义方式与铺层覆盖策略

目前较为常用的线性函数法［22］在定义简单的同时，也能满足丝束的连续性要求［3］。尺寸为a×b的变刚度层合板纤维路径如图1 所示，首先定义一条通过平板中心的参考曲线，标记为〈T0|T1〉，表示该曲线在x=0 与x=±a/2 处的切线与x轴的夹角分别为T0与T1。

图1 变刚度复合材料层合板纤维路径定义示意图Fig.1 Schematic diagram of fiber path definition of variable stiffness composite laminates

根据定义，参考曲线〈T0|T1〉经过原点并关于原点中心对称，且曲线与x轴的夹角θ随x线性变化，于是

另一方面，参考曲线的斜率可表示为

将式（1）代入式（2）并积分即可得到曲线的表达式：

为实现铺层覆盖，常用的方法包括平移法与平行法两种方案，其中平移法通过将参考曲线沿y轴等距平移的方式实现（图2（a）），平行法的移动方向则为参考路径中心处的切线方向（图2（b）），保证相邻丝束间距离处处相等［3］。由于采用平移法铺设的层合板相比于平行法具有更优越的屈曲性能［23］，且平行法易造成纤维丝褶皱［24］、相邻丝束间的扭结现象［25］，因此变刚度层合板主要采用平移法制造。

图2 纤维铺放方法Fig.2 Methods of fiber placement

1.2 间隙与重叠缺陷的形成机理

由于丝束带存在一定宽度，且铺放过程中铺丝头总是垂直于参考路径方向，故丝束带在y方向上的宽度随参考路径的斜率而变化。铺放时相邻丝束带的交接处存在截面突变，同时丝束带边缘存在角度偏差［26］，因此采用平移法铺设并满足满铺覆性要求时相邻丝束带间必然会存在夹角，从而产生间隙与重叠缺陷（图3）。在含缺陷的变刚度层合板中，间隙区域由性能较差的树脂填充，易发生基体开裂；重叠区域则会导致层合板厚度不均，从而影响表面平整度，可通过最外层采用±45°铺层的方式提高表面的平整度［27］。

图3 丝束带间隙与重叠区域Fig.3 Gaps and overlap areas between tows

目前主要采用丝束剪切/重送技术减少间隙与重叠区域，通过丝束覆盖比例（图4）控制切断与重送位置，可得到任意比例覆盖的铺层，其中0覆盖为完全间隙，100%覆盖为完全重叠，主要研究完全间隙（图4（a））与完全重叠（图4（c））两种覆盖比例。同时为避免缺陷在同一位置积聚，可采用铺层偏移法对相同角度的铺层进行偏移［28］。图5［29］为实际制得的含缺陷铺层，分别对应完全间隙与完全重叠两种覆盖比例策略。

图4 缺陷覆盖比例示意图Fig.4 Diagram of defect coverage ratios

图5 含缺陷的变刚度层合板［29］Fig.5 Variable stiffness laminates with defects［29］

1.3 基于剪切/重送技术的丝束带缺陷分布计算方法

基于丝束剪切/重送技术得到的含间隙或重叠缺陷的丝束带如图6 所示，均由6 根丝束组成。为避免出现严重影响层合板性能的大区域间隙（图3（a）），平移距离S为

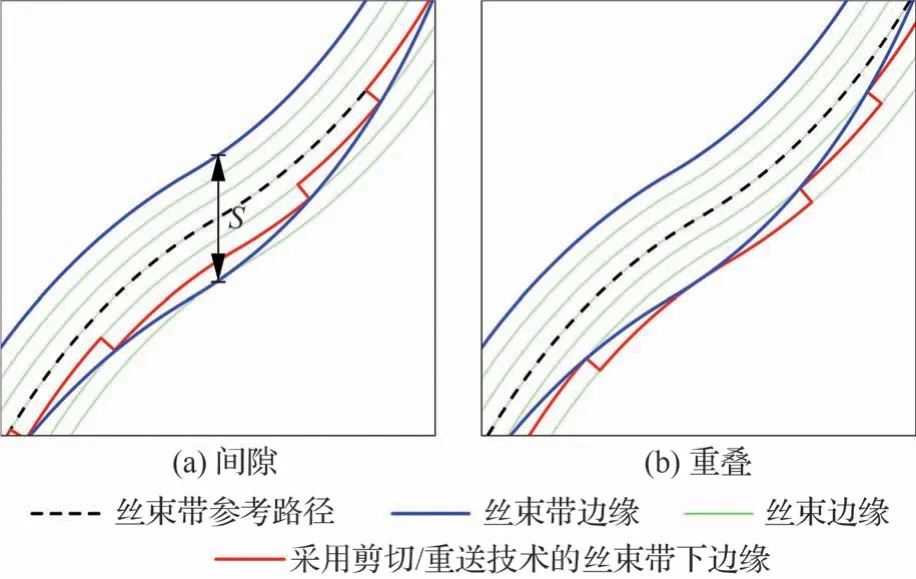
图6 采用丝束剪切/重送技术得到的丝束带Fig.6 Tows obtained by tow cut/restart technology

式中：w为丝束带宽度。

将该丝束带下边缘轨迹记为y1=f1（x），下一丝束带上边缘轨迹记为y2=f2（x）。采用完全间隙铺设策略时，将下边缘轨迹与下一丝束带的上边缘轨迹进行比较，若某一部分y1＜y2，则将该部分下边缘向上偏移一个丝束宽度（即采用剪切技术），直至轨迹上的每一点均满足y1＞y2（图7）；采用完全重叠铺设策略时，将下边缘所在丝束的上边缘记为y3=f3（x）并与下一丝束带的上边缘进行比较，若某一部分中y3＜y2，则该部分下边缘向上偏移一个丝束宽度，直至轨迹上的每一点均满足y3＞y2。

图7 间隙铺设策略流程图Fig.7 Flow chart of gap laying strategy

2 考虑缺陷占比的含缺陷材料性能的计算方法

2.1 RVE 模型的周期性边界条件

均匀化理论通过引入具有代表性的微元建立RVE 模型对整体模型进行分析。为保证在RVE 模型边界上应力与应变的连续性，需采用周期性边界条件。Xia 等［30］提出了一种统一的周期性边界条件，该条件下单胞的一对平行表面在变形前后保持平行，即保证了连续性要求，其数学表达式为

典型的六面体RVE 模型如图8 所示，该单胞的体积为V。

图8 典型六面体RVE 模型Fig.8 A typical hexahedral model of RVE

通过式（5）进行有限元二次开发，对单胞模型施加周期性边界条件，设置顶点的边界条件为

式中：Ui为i方向上的位移；Ri为绕i轴的转角。将位移载荷δi施加于单胞的顶点（B点、D点与E点分别施加x、y与z方向的载荷），此时单胞的平均应力与平均应变为

式中：σi与εi分别为单胞的应力与应变。由于采用式（7）中的平均应力与平均应变计算得到的应变能与均匀化前非均质单胞的应变能相等［31］，因此单胞的应变能U可表示为

同时施加的位移载荷产生顶点上的支反力为Fi，于是外力所做的功W为

由于应变能与外力所做功相等，联立式（8）与式（9）得

最终根据弹性模量与泊松比的定义得等效弹性模量Ei与泊松比νij为

类似地，通过在单胞顶点D点上分别施加x与z方向的位移载荷得到等效剪切弹性模量G12与G23、在B点上施加z方向的位移载荷得到G13［32］：

2.2 含间隙或重叠缺陷的简化模型

为简化含缺陷层合板的有限元分析，假设缺陷均位于材料简化模型的中心处，忽略缺陷位置对含缺陷材料性能的影响，即假设含相同缺陷占比的材料具有相同的弹性性能。按缺陷占模型面积的百分比建立含缺陷的材料简化模型如图9所示。对于间隙缺陷（图9（a）），将简化模型中心处的区域按百分比填充树脂材料，其余区域赋予无缺陷材料性能；对于重叠缺陷（图9（b）），模型厚度为间隙模型的两倍，将其沿厚度方向切割为两层，而后对第1 层及第2 层对角的两个区域按百分比赋予树脂材料，其余部分赋予无缺陷材料属性。

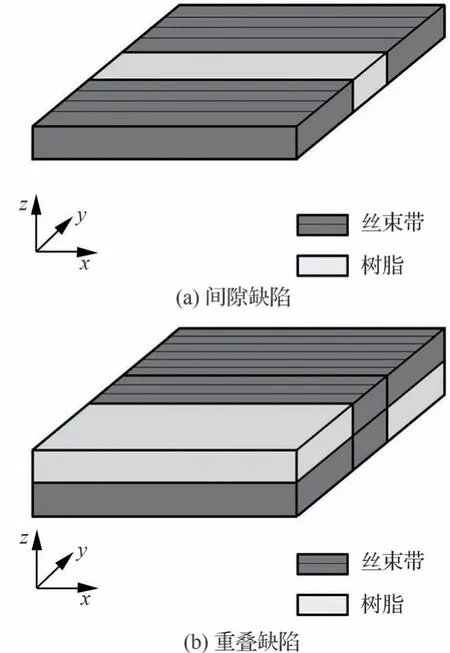
图9 含缺陷材料简化模型Fig.9 Simplified model of material with defects

含相同缺陷占比的材料可视为由图9 的含缺陷材料简化模型按周期性排列得到。以图10（a）所示间隙材料为例，该模型包含4×3 个含间隙缺陷的材料简化模型，具有周期性，可通过任一胞元（图10（b））平移得到，因此含相同缺陷百分比材料的力学性能可通过RVE 模型计算。

图10 含相同间隙缺陷占比的材料模型Fig.10 Model of material with the same defect proportion of gaps

2.3 厚度改变的重叠缺陷等效方法

由于在含重叠缺陷层合板的实体模型中，采用增加铺层的方式模拟含重叠缺陷的区域会导致缺陷单元厚度增加，造成同一铺层中单元的不连续，因此需对重叠缺陷材料的简化模型进行进一步等效，使含重叠缺陷的单元厚度与无缺陷单元一致。等效前后重叠缺陷材料模型的特征长度li与的关系为

为保证含重叠缺陷材料的受力状态在等效前后保持不变，等效后单元所受轴向力及平均应变可表示为

根据弹性模量的定义，结合式（13）与式（14）得到等效后的弹性模量为

同理可得等效后的泊松比与剪切弹性模量为

2.4 缺陷占比与材料弹性性能的关系

以碳纤维环氧树脂复合材料AS4/977-3 为例，以10%为1 级计算含不同缺陷百分比材料的弹性性能，得到缺陷占比与材料弹性性能之间的关系。建立1.0 mm×1.0 mm×0.1 mm 的有限元模型，采用C3D8R 实体单元计算，通过二次开发建立模型的周期性边界条件。AS4/9773 的材料性能如表1 所示，CYCOM 977-3 环氧树脂的材料性能如表2 所示，定义无量纲化后材料的弹性性能XN为

表1 AS4/977-3 材料性能Table 1 Material properties of AS4/977-3

表2 CYCOM 977-3 材料性能Table 2 Material properties of CYCOM 977-3

式中：Xdefect为含缺陷材料的弹性性能；Xperfect为无缺陷材料的弹性性能。

含不同间隙与重叠缺陷百分比的材料性能如图11 与图12 所示，对于含间隙缺陷的材料，材料性能随缺陷占比的增大而劣化，而含重叠缺陷的材料性能则随着缺陷的增加而增强。图11 中间隙缺陷占比为100%处代表完全间隙材料，此时材料性能即为树脂材料性能；间隙缺陷占比为0 处代表无缺陷材料，此时无量纲化后材料的性能为1。图12 中重叠缺陷占比为100%处代表完全重叠材料，此时无量纲化后材料的性能为2；重叠缺陷占比为0 处代表无缺陷材料，此时的等效性能与无缺陷材料性能存在偏差，故对缺陷占比为0 的单元赋予无缺陷材料的性能。对于缺陷占比趋于0 的单元，由于变刚度层合板有限元模型中的单元角度通常采用离散法定义，网格尺寸过大会导致单元内的角度与实际纤维角度存在较大偏差，而在满足角度精度要求的网格尺寸下重叠缺陷占比趋于0 的单元极少，因此对有限元模型的总体性能几乎没有影响。

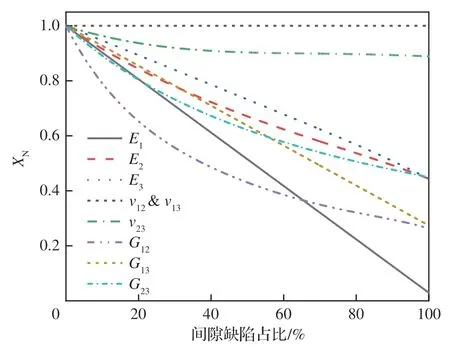
图11 不同间隙占比材料的无量纲弹性性能Fig.11 Dimensionless elastic properties of material with different proportions of gap

图12 不同重叠占比材料的无量纲弹性性能Fig.12 Dimensionless elastic properties of material with different proportions of overlap

3 含缺陷变刚度层合板模型的验证

3.1 含缺陷层合板模型

通过参考文献［13］的试验验证本文方法的有效性，根据试验在ABAQUS 软件中创建含缺陷层合板有限元模型，试件尺寸为622.3 mm ×660.4 mm，铺层角度为［±45/（±〈30|60〉）4］s，共20 层，厚度为3.88 mm，单丝束宽度为3.175 mm，丝束带中的丝束数为24。试件类型包括间隙层合板（采用剪切/重送技术且覆盖比例为0）及重叠层合板（不采用剪切/重送技术且覆盖比例为100%）。为研究网格尺寸对预测精度的影响，设定网格尺寸分别为5.0、12.7、20.0 mm，单元类型为C3D8R 实体单元。Wu 等［13］采用了常规壳单元，网格尺寸为12.7 mm，通过单元中心点坐标判断缺陷类型，对于含重叠缺陷的层合板赋予缺陷单元两倍铺层厚度，对于不含重叠缺陷的层合板则忽略缺陷影响。

残余热应力会影响层合板的力学性能［33］，对于T0＜T1的变刚度层合板，残余热应力在中心区域的轴向截面合力为正，受均匀轴向压缩载荷时中心区域的轴向压应力降低，有利于提高层合板的屈曲载荷［28］，因此在变刚度层合板屈曲性能的分析过程中需考虑残余热应力的影响。采用线性冷却的方式模拟了固化时热应力的作用，设定固化由176.67 ℃降至室温21.11 ℃。

根据试验采用的夹具（图13（a）［13］）设置有限元模型的边界条件，如图13（b）所示，上下两端为固支，约束层合板在x方向与z方向的位移，并在顶端施加位移载荷y=y0；侧边为简支，距两侧6.35 mm 处（图13（b）中点划线处，共4 条，仅标注单面，下同）约束面外位移z=0。同时距上下顶端分别为12.7、25.4 mm 处（图13（b）中虚线处，共8 条）约束面外位移z=0，并约束左右端点（图13（b）中圆点处，共16 个）x方向的位移。

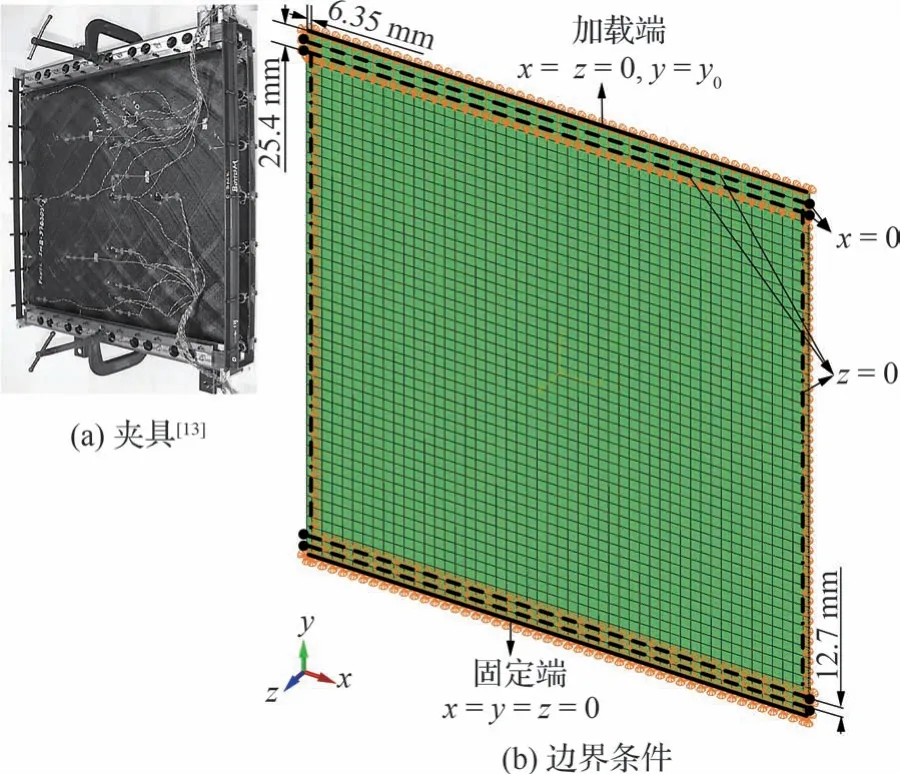
图13 夹具及模型边界条件Fig.13 Support fixtures and boundary conditions of model

3.2 基于二值图像法的缺陷定位与占比识别

通过1.3 节中丝束带缺陷的计算方法预测的缺陷分布如图14 所示，不同铺层角度对应不同的分布情况。而后采用ABAQUS 软件联合Python脚本文件获取各个网格的顶点坐标以及铺层位置，基于二值图像法计算单元内阴影面积的占比（即为缺陷占比），同时构建含不同缺陷占比的单元集合（以1%为1 级），最终结合含缺陷材料性能的计算方法赋予不同单元不同的材料性能。

图14 预测的缺陷分布Fig.14 Predicted defect distributions

将采用二值图像法识别的有限元模型中缺陷的分布情况（图15）与预测的缺陷分布（图14）进行比较，模型中的红色网格表示含缺陷单元，含间隙缺陷的模型选取了缺陷占比大于40%的单元，含重叠缺陷的模型则选取了缺陷占比为100%的单元。对比结果表明二值图像法能对有限元模型中的缺陷进行准确定位与占比识别。

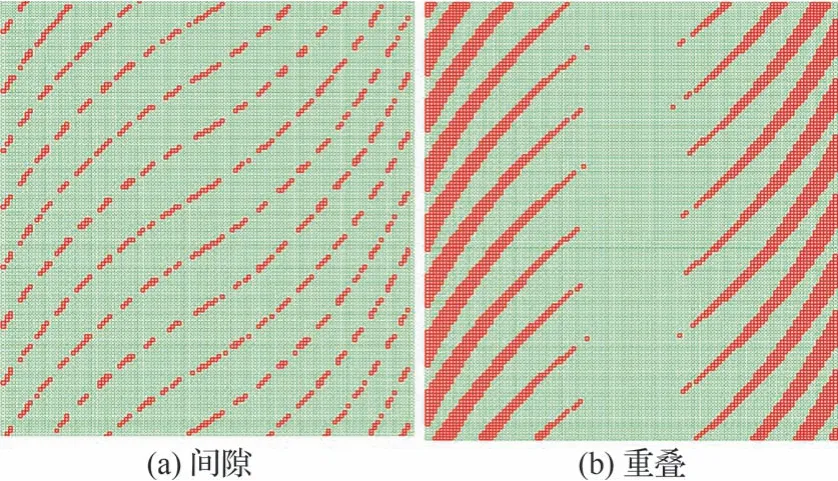
图15 有限元模型缺陷分布Fig.15 Defect distributions in FEM

3.3 缺陷层合板有限元模型屈曲性能计算与对比

对结构进行屈曲分析的方法包括线性特征值屈曲分析与非线性屈曲分析，其中非线性屈曲分析更符合实际情况，预测结果更加准确［34］，故采用了非线性屈曲分析方法。对于算例中的变刚度层合板，需在分析中同时引入残余热应力与几何缺陷，几何缺陷的模态比例因子取为层合板厚度的1%［35］。针对载荷-位移曲线的显著非线性特征，Wu 等［13］结合试验将屈曲载荷记为斜率为刚度0.995 倍的正比例函数与载荷-位移曲线的交点对应的载荷，即基于载荷-位移曲线的“刚度过渡点”法［29］。采用该方法得到考虑残余热应力的含缺陷层合板屈曲载荷、试验载荷及Wu等［13］预测的载荷如表3 所示，其中方案1、方案2 与方案3 分别对应网格尺寸为5.0、12.7、20.0 mm时本文方法的预测结果。3 种网格尺寸下的载荷位移曲线相近，故仅以方案1 为例与试验进行对比，两种类型层合板的载荷-位移曲线如图16 所示，可见本文方法预测得到的载荷-位移曲线与试验［13］结果吻合良好，且预测精度受网格尺寸影响较小，能有效降低计算成本。

表3 含缺陷层合板屈曲载荷对比Table 3 Comparison of buckling loads of laminates with defects

图16 变刚度层合板载荷-位移曲线Fig.16 Load-displacement curves of variable stiffness laminates

为进一步验证本文方法的有效性，对文献［27，36-37］中的变刚度层合板及开孔板的屈曲性能进行预测（网格尺寸均为5 mm），与试验的对比情况如表4 所示，结果表明本文方法预测结果与试验值的误差在7%以内。

表4 含缺陷层合板与开孔板屈曲载荷对比Table 4 Comparison of buckling loads of laminates with defects and open-hole laminates with defects

本文方法主要通过二值图像法计算结构中不同区域的缺陷占比，而后赋予有限元模型中对应的单元不同的缺陷材料属性，可用于平板、开孔板、加筋板等结构拉、压、剪等性能的分析。

4 结论

1）分析了制造过程中不可避免的间隙与重叠缺陷的形成机理，采用缺陷占比表征局部区域内材料的含缺陷程度，基于RVE 提出了含缺陷材料的简化模型，从而建立了含缺陷材料性能的计算方法。

2）采用二值图像法对层合板中间隙与重叠缺陷进行了定位与占比识别，该方法能有效判断模型中缺陷的位置并计算每一单元的缺陷占比。而后结合所提性能计算方法赋予不同缺陷占比的单元不同的材料性能。

3）计算了含缺陷层合板的屈曲性能并与试验进行对比，结果表明本文方法计算得到的屈曲性能与试验吻合良好，预测结果的误差在7%以内，验证了本文方法的有效性。同时本文方法的预测精度受网格尺寸影响较小，能有效降低计算成本。