临近空间高超声速飞行器武器投放影响因素
崔玉红,徐艺哲,吕凡熹,赵飞,张宇佳,孙佳濛,左光
1.天津大学 机械工程学院,天津 300072
2.中国空间技术研究院 钱学森空间技术实验室,北京 100094
3.蓝箭航天空间科技股份有限公司,北京 100176
临近空间是指距海平面20~100 km 高度的空域,该高度空域拥有着大气平流层、中间层、增温层,绝大部分介质成分可以看为均质大气。由于特殊的环境介质和空间位置,临近空间飞行器近年来一直受到许多国家的重视,成为了各国踊跃竞争的军事热点[1-2]。高超声速一词最早于1946 年钱学森先生在《论高超声速相似律》中提出,通常将马赫数Ma>5 的流动称为高超声速流动。目前世界各国通过采用先进的气动外型,积极开展临近空间高超声速飞行器的相关研究[3-4]。但是在研究过程中均遇到了诸如激波/边界层干扰、真实气体效应和多物理场耦合等关键问题[5-6]。进一步,高超声速分离期间还会产生级间干扰和激波干扰等复杂的流动现象,不但影响飞行器的气动特征以及分离物的飞行姿态,还会严重影响载机及投放物的安全[7-9]。因而,临近空间高超声速飞行器武器投放面临着飞行环境复杂、高超声速飞行、多体分离干扰等棘手的问题,开展相关研究具有十分重要的实际意义和应用前景。
临近空间高超声速分离问题主要分为级间分离、子母弹抛撒、机载导弹分离等。同时,多体分离问题的研究方法主要分为理论分析、数值模拟、地面试验、飞行试验。Malmuth 等[10-11]运用细长旋成体理论研究了跨声速条件下导弹分离的舱内阶段、穿越剪切层阶段、舱外阶段。发现导弹投放后的姿态和导弹直径密切相关,仅当导弹直径等于9.53 mm 时能在Ma=1 条件下正常投放。然而,理论分析方法仅能描述低速投放的情况,对高速内埋式弹舱武器投放不再适用。飞行试验是研究武器投放最为直接和有效的方法,各国为了抢占制空权,正在紧锣密鼓地筹备超高声速飞行器和超高声速导弹的飞行试验。目前,飞行试验代价昂贵,危险极大,试验数据一般不对外公开,通常作为研究的最终验证手段[12-13]。
地面试验、数值模拟是目前超声速/高超声速飞行器分离问题研究中最为常见的2 种方法,并且都具备可以模拟非定常效应和有效可靠的优点。地面试验包括风洞投放试验(Wind Tunnel Drop Testing,WTDT)、风洞捕获轨迹试验(Captive Trajectory System Testing,CTS)、风洞自由飞试验(Wind Tunnel Free Flight Testing,WTFFT)等[14]。宋威等[15-16]通过WTDT方法,研究了F22 开式弹舱在不同初始分离角速度、马赫数、攻角等因素下的武器投放过程;同时,结果分析中修正了垂直位移,认为风洞结果较为保守,30 rad/s 的初始分离角速度更有利于导弹分离等。董金刚等[17]通过CTS 方法和纹影显示技术研究了初始分离速度、分离高度、载弹尾舵状态对内埋式武器超声速分离的影响。结果表明,在Ma=1.5 和载机迎角为2.2°条件下,无初始分离速度会出现不安全分离的趋势;分离高度降低会导致载弹不安全分离趋势提前;尾舵折叠不利于载弹姿态控制的结论。林敬周等[18-19]在Φ=1 m 高超声速风洞多体分离试验系统的基础上建立了双轨迹捕获试验系统,是国内首次形成高超声速风洞双分离轨迹捕获试验,该项试验技术已经达到了国际先进水平。WTFFT 方法原理是预先将分离体紧锁为一体,并在风洞流场中发射,经过观察窗时触发分离装置,由高速相机记录多体分离过程。该方法能够充分反映多体分离过程的运动和气动力耦合规律,非常接近实际飞行环境。WTFFT 方法常用于子母弹抛撒和级间分离等分离体和母体质量差别不大的分离研究,一般不用于飞行器武器分离的研究[20]。总之,地面试验虽然直观可靠,但是目前高超声速试验装备仍然存在着性能局限、试验时间限制、试验模型尺寸限制等问题。
数值模拟方法是近些年研究临近空间高超声速飞行器的主要手段,既避免了试验条件的限制,也减少了高昂的试验费用。杨俊和张新慧[21]通过重叠网格技术,模拟了飞行高度25 km,飞行速度Ma=3.3,3.5,3.7 的内埋式武器重力投放。结果表明,3 种飞行速度下,导弹均能正常在弹舱内分离。低头安装角有利于弹体和载机分离,安装角为-4°时,俯仰角较为稳定,更有利于分离。李骞等[22]利用嵌套网格方法,模拟了Ma=3.7、高度为25 km 的条件下,重力舱内投放、舱内弹射投放、舱外重力投放3 种内埋式武器分离方式的分离过程,认为舱内弹射是最安全和快速的分离方式。同时发现舱外重力投放方式,在投放之初就受到高速来流的作用,导弹受到抬头力矩后呈现明显的倾斜姿态,严重威胁载机安全。赵飞等[23]研究了类X-43A 飞行器的分离问题,讨论了初始攻角和弹射力大小对级间分离的影响,得出小攻角或负攻角对级间分离存在有利的影响、弹射力对分离速度有显著影响等结论。孙佳濛等[24]提出了临近空间高超声速飞行器4 种武器投放方式,载机飞行高度25 km,飞行速度Ma=4.0~10.0。结果表明,导弹直接外挂投放方案成功率最高,气动干扰最小,是一种较为可行的临近空间高超声速武器投放方案。除此之外,鲜有利用数值模拟方法进行高超声速武器分离或投放的研究,这是因为与其他分离问题相比,数值模拟方法求解机载导弹分离问题还存在诸多困难。
截至目前,采用数值模拟研究临近空间高超声速飞行器的武器投放仍然存在很多问题,例如真实飞行环境模拟的复杂性、机弹分离影响因素的多样性、流体-动力学耦合求解方法的复杂性和高超声速数值模拟的收敛性等,这些问题都是临近空间高超声速飞行器的武器投放的关键问题。因此,为了深入研究临近空间高超声速飞行器武器投放的可行性,本文在孙佳濛等[24]的研究基础上,进一步对临近空间高超声速飞行器的飞行高度Hb、载机攻角α、导弹初始安装角θ、弹射力大小F、弹射力作用时间t共5 个影响因素进行研究。建立了包括 3 种飞行高度Hb=25,30,35 km、5 种载机攻角α=-4°,-2°,0°,2°,4°、4 种导弹初始安装角θ=-3°,0°,3°,5°、4 种弹射力大小F=5,10,15,20 kN、4 种弹射力作用时间t=0.01,0.02,0.05,0.10 s 在内的计算模型和气动模型,通过数值模拟的方法详细研究武器投放的非定常特征。
1 计算模型与计算参数
1.1 计算模型
载机及导弹几何模型见图1,机身整体为纺锤形,无平尾。机翼采用NACA6140 翼型,前缘后掠50°,后缘前掠15°。导弹由挂架伸出,位于机翼正下方。导弹长2 m、直径0.2 m、重200 kg、弹头前端为半锥角18°的圆锥。弹翼采用NACA0008翼型,4 片尾翼呈X 形分布。定义机身轴线方向为Y轴,正方向指向机头,纵向对称面为YOZ平面,X轴方向由右手螺旋法则获得,导弹基准轴线与Y轴平行,导弹头部指向Y轴正方向。同时定义导弹尾翼所在平面为基准面Ω,位置示意图如图1。
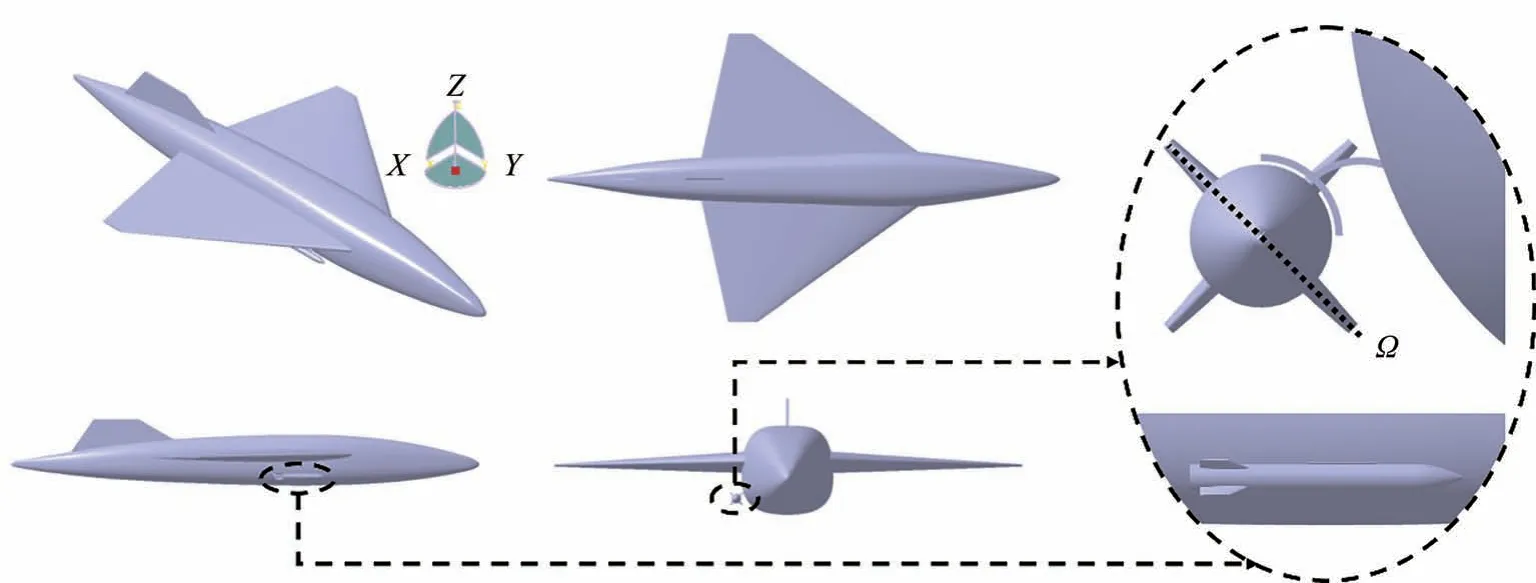
图1 载机及导弹几何模型Fig.1 Geometry model of aircraft and missile
载机攻角α是指来流速度矢量在机体坐标系中YOZ平面上的投影对Y轴的夹角。导弹初始安装角θ为导弹轴线与基准面Ω之间的夹角,定义导弹轴线方向指向机身时安装角为正,反之为负。导弹初始安装角直接影响导弹挂载期间所受气动力,进而可能影响导弹外伸和弹射过程的稳定性能。载机攻角和导弹初始安装角的角度变化示意图见图2。
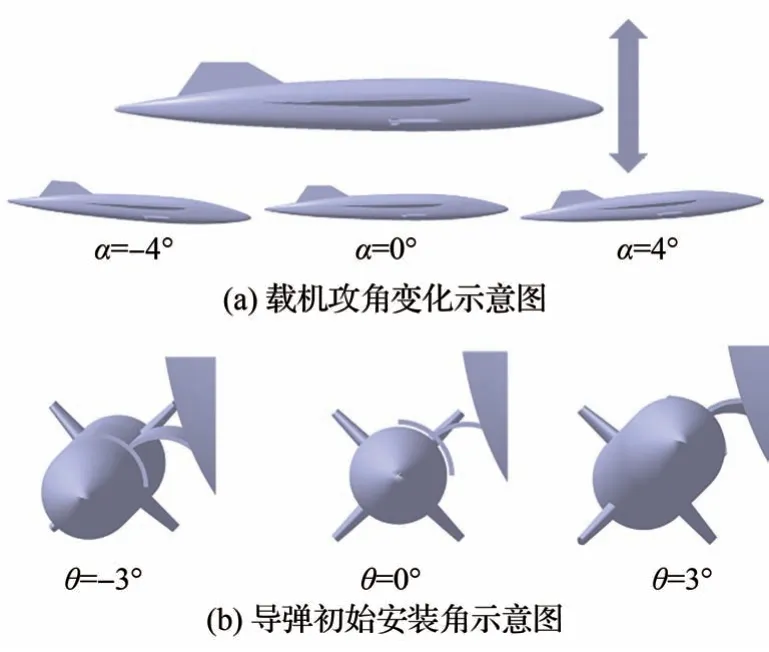
图2 载机攻角和导弹初始安装角示意图Fig.2 Schematic diagram of aircraft angle of attack and initial installation angle of missile
高超声速飞行器在飞行期间,会产生复杂的黏性干扰、强压缩高温流动、激波干扰等流动现象。武器投放过程中,复杂的流场对弹体运动产生强烈的气动干扰,同时弹体的运动和流场相互作用,产生复杂的非定常效应。因此,开展高超声速飞行器武器投放需要采用流体-动力学双向耦合的求解方法,才能较为准确地对武器投放过程进行数值模拟。利用有限体积法对非定常Navier-Stokes 方程进行求解,同时采用密度基求解器、二阶迎风通量格式、双时间步隐式时间推进方法。流场计算中采用了广泛应用于高超声速流动仿真的SST(Shear Stress Transport)k-ω湍流模型。该湍流模型在湍流黏度的定义中考虑了湍流剪切应力的传递,使其拥有更广泛的适用范围,比标准k-ω模型和BSL(BaseLine)k-ω模型更准确和可靠。SSTk-ω湍流模型的湍动能输运方程和湍流耗散方程[25-29]为
式中:ρ为大气密度;k、ω为湍动能、湍流耗散率;ui为速度矢量;Γk、Γω为由k、ω引起的有效扩散率;Gk、Gω为湍流动能和湍流耗散率的生成项;Yk、Yω为由k、ω引起的湍流耗散;Sk、Sω为人为定义的源项;Gb、Gωb为浮力对湍流的影响。
六自由度控制方程[30]为
式中:νG质心平动速度;fG为重力矢量。
质心转动速度计算公式为
式中:L为惯性张量;MB为物体力矩矢量;ωB为刚体角速度矢量。
流体-动力学双向耦合求解的计算过程为
1)根据物体动力学运动状态更新相应的物面边界条件和网格。
2)根据更新后的流体域进行虚拟时间步推进获得新的流场。
3)根据更新后的流场求解动力学方程。
4)重复过程1)~3)虚拟时间步推进过程,直到流场和物体运动均收敛。
5)获得该时间步的流场及动力学求解结果。
6)开始下一时间步的计算。
图3 为数值模拟的计算域及边界条件,入口采用压力远场边界条件,环境压力、马赫数、环境温度等参数由1.2 节给出;出口采用压力出口边界条件;机身为绝热无滑移的壁面边界条件。图4为机身周围网格及机头边界层网格,计算域整体网格数量1 600 万,物面y+数值均为0~3,网格最大偏斜度均在0.9 以下。

图3 计算域及边界条件Fig.3 Computational domain and boundary conditions
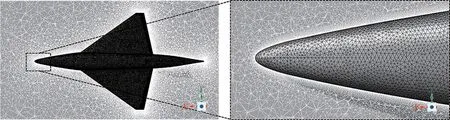
图4 机身周围网格及机头边界层网格Fig.4 Mesh around aircraft and nose boundary layer
1.2 计算参数及验证
随着飞行高度的提升,载机所处临近空间的大气温度、重力加速度、大气密度、大气压力等参数设置都发生显著变化[31]。其中,与海拔相关的独立参数大气温度T和重力加速度g参数选择如下。
大气温度T由图5[31]1976 年美国标准大气温度与位势高度之间的关系计算得出,根据文献[31]中提供的公式可以计算25、30、35 km 高度的温度分别为221.65、226.65、237.05 K。重力加速度其中g0=9.806 65 m/s2,r0=6 356 766 m,Z为几何高度。同时,由大气温度T、重力加速度g可以得到大气压力:
式中:g′0、M0、R*为确定的单值常数;LM,b、Hb、TM,b分别为温度梯度、位势高度、分子标度温度,均为多值常数。
进一步,由大气温度T和大气压力P可以计算得到大气密度其中M0=28.964 4 kg/kmol,R*=8.314 32×103J/(mol·K)。25、30、35 km高度下的大气密度、重力加速度、大气温度、大气压力见表1。其他计算参数如载机参数和载机攻角等见表2。

表1 高度25、30、35 km 下环境参数Table 1 Environmental parameters at altitude of 25,30 and 35 km

表2 载机、导弹信息和计算参数Table 2 Information and calculation parameters of aircraft and missile
根据课题组前期经验[24],采用美国空间实验室的机翼-挂架-带翼导弹模型(Wing/Pylon/Finned-Store,WPSF)[32]进行计算方法验证。前期工作[24]对载机、导弹划分不同数量的网格来进行网格收敛性验证,采用不同时间步长完成了瞬态计算时间步长的精确性验证。结果表明,上述的计算方法完全可以对机载导弹分离问题进行有效模拟,并且1 600 万的网格数量、0.001 s 的时间步长既满足精确性要求又保证计算效率。
2 结果分析与讨论
2.1 攻角对导弹投放的影响
载机在临近空间高超声速飞行时,攻角一方面影响载机本身的飞行轨迹,另一方面影响机身附近流场和压力分布,2 个因素共同影响着导弹和载机的相对位置变化。假设载机在机弹分离过程中飞行姿态保持稳定,不会在分离过程中发生明显变化。图6 为Ma=8 时不同攻角下涡结构、图7 为Ma=8 时不同攻角机身腹部压力云图,图8 为不同工况下机身周围流线变化。载机以正攻角飞行时,分离涡位于机翼上方,涡内压力等于外部气流的压力。随着攻角的增加,机身前缘驻点位置逐渐下移,机身尾部的分离区逐渐扩大,机翼下方压力明显增加。正攻角时机身和导弹的升力指向Z轴正向,负攻角时方向相反。因而正攻角下导弹投放后可能产生偏向载机的位移和角位移,严重影响导弹分离的安全性,需要进一步进行分析。

图6 Ma=8 时不同攻角下涡结构Fig.6 Vortex structures at different angles of attack for Ma=8
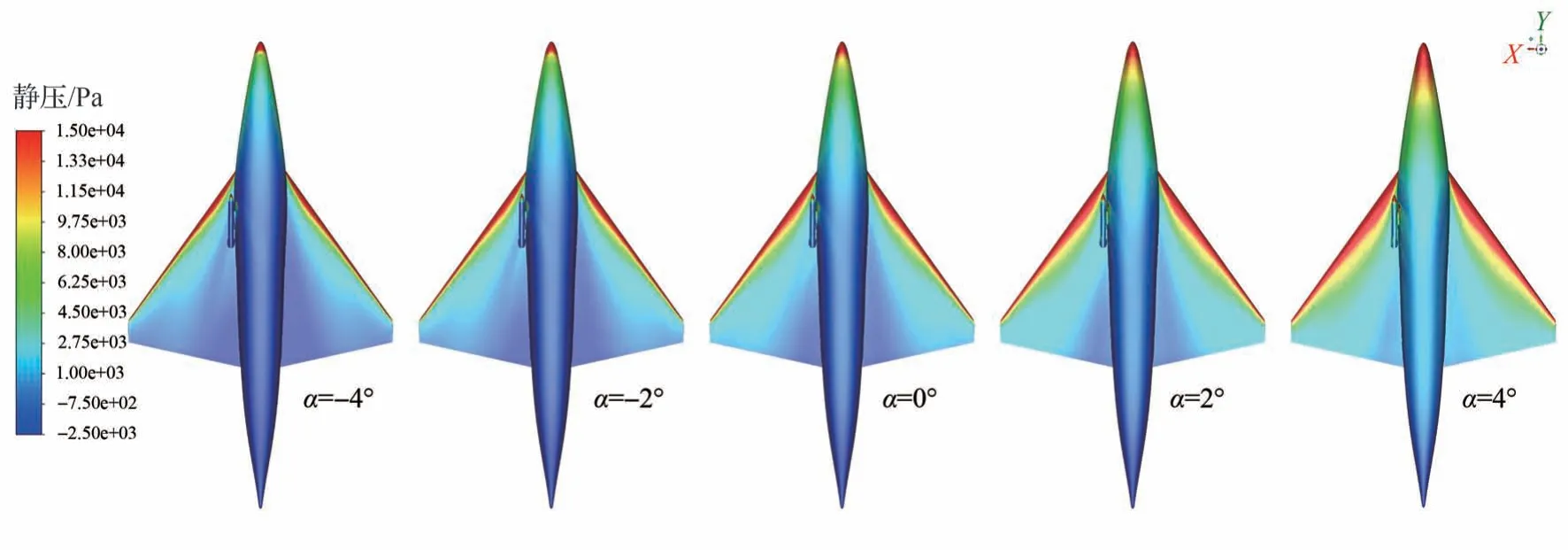
图7 Ma=8 时不同攻角机身腹部压力云图Fig.7 Pressure contour on aircraft belly at different angles of attack for Ma=8
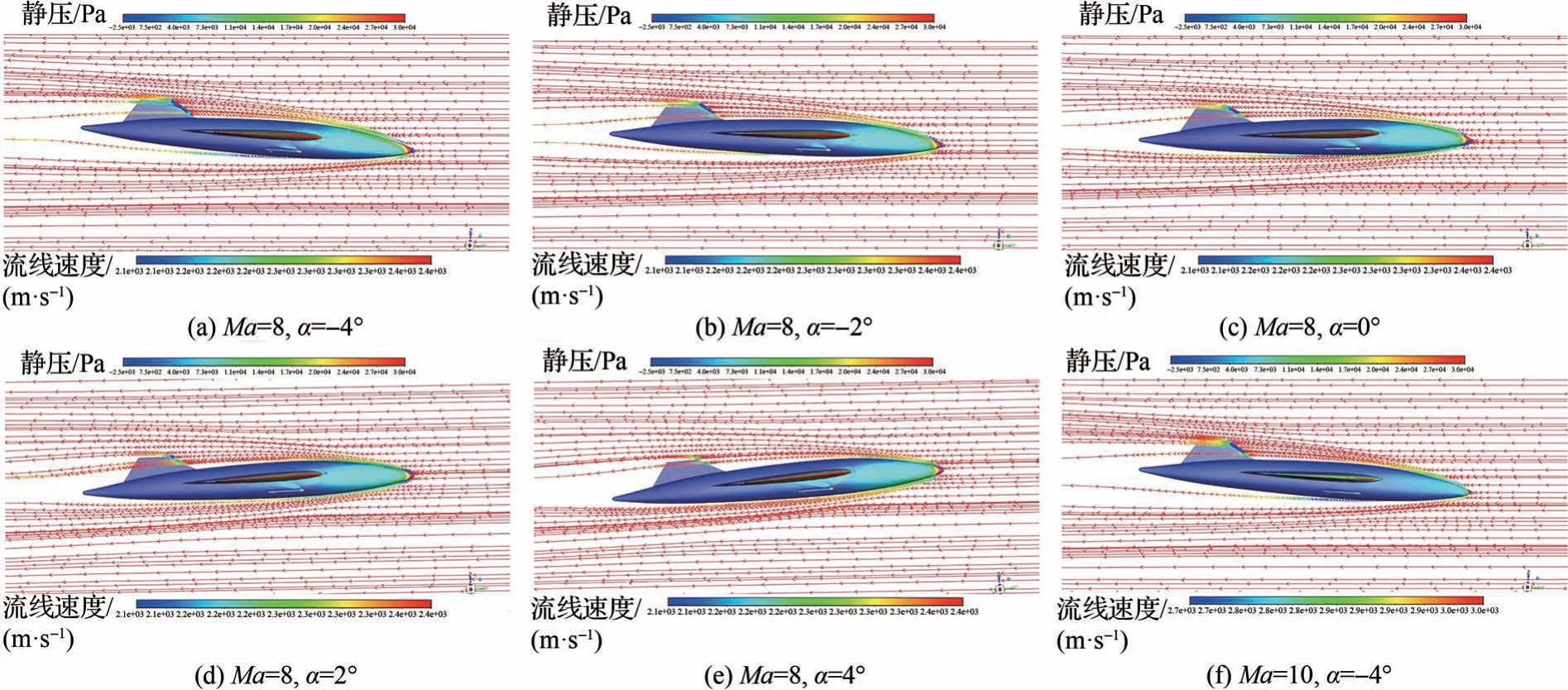
图8 不同工况下机身周围流线变化Fig.8 Streamline variation around aircraft under different conditions
图9 为5 种攻角下导弹的位移、角位移、气动力、气动力矩变化。根据图1 建模坐标及说明可以看出X轴正向位移远离机身,Z轴负向位移远离机翼,2 种位移都有利于导弹快速安全分离。Y轴为导弹轴向方向,该方向上位移对导弹投放的安全性影响相对较小。导弹X轴正方向角位移指向机翼,Z轴正方向角位移指向机身,2 种角位移都不利于机弹分离的安全。导弹Y轴方向角位移为导弹轴向转角,对载机和导弹安全没有直接影响。通过图9 可以看出,Ma=8,10 时所有工况均正常弹射。不同攻角下导弹位移变化趋势基本一致,仅在数值变化上存在差别,并且导弹在X、Z轴方向上的位移均为有利于机弹分离。不同攻角下导弹角位移变化差距较大,甚至出现方向上的差别。
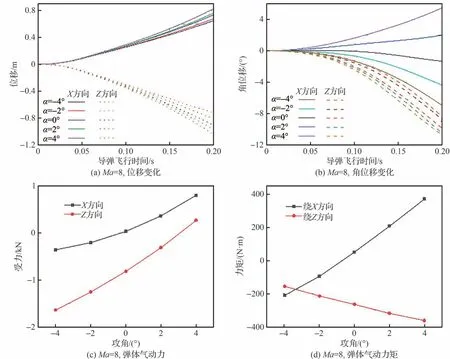
图9 5 种攻角下导弹的位移、角位移、气动力、气动力矩变化Fig.9 Variation of missile displacement,angular displacement,aerodynamic force,and aerodynamic moment at five angles of attack
以Ma=8 武器投放为例,表3 为导弹飞行时间П=0.2 s 时不同攻角下导弹位移和角位移对比。可以看出当载机由正攻角调整为负攻角时,X轴正向位移降低9.33%,Z轴负向位移增加27.35%。这是由于当载机以正攻角α=4°进行高速飞行时,机身和导弹均受到明显的Z轴正向力,受力变化如图9(c)、图9(g)。载机攻角越大,受到的Z轴正方向作用力越大。这使得正攻角下导弹在无外力状态时存在明显的向机翼运动的趋势。与此同时,载机由正攻角调整为负攻角时,X轴负向角位移增加227.14%,Z轴负向角位移减少22.08%。其中,当载机以攻角α=4°飞行,在П=0.2 s 时导弹X轴方向角位移为5.49°,是武器分离严重的安全隐患。不仅如此,载机攻角α=2°,0°、П=0.2 s 时,导弹X轴方向角位移分别为-4.39°、-1.35°,导弹同样出现抬头趋势。当载机由正攻角调整为负攻角时,安全隐患消失。这是由于载机在以正攻角高速飞行时,导弹直接暴露在来流空气中,正攻角直接使导弹受到了Z轴正向力和X轴正向力矩。X轴正向力矩是导弹的抬头力矩,正攻角下导弹产生的抬头趋势一直贯穿始终,是机弹分离严重的安全隐患。载机以负攻角飞行时,导弹在机翼下表面产生的膨胀波低压区内,受到来流的直接作用效果减弱,因而负攻角时导弹X、Z轴方向的转角都有利于机弹分离。
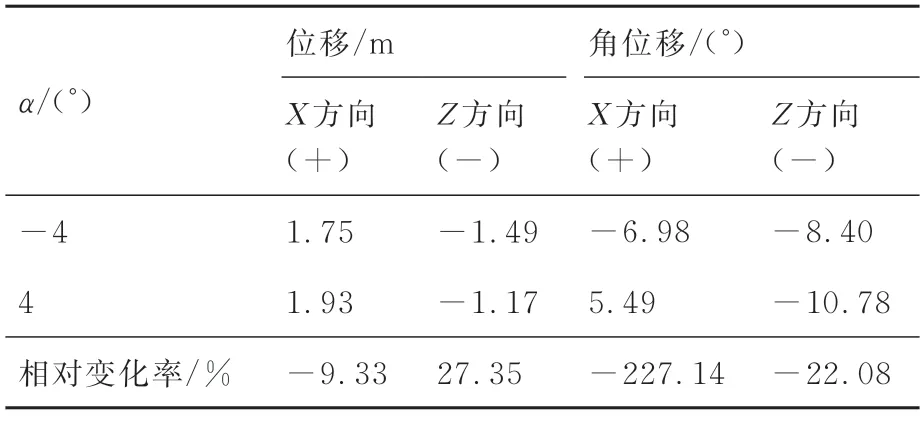
表3 П=0.2 s 时不同攻角下导弹位移和角位移对比(Ma=8)Table 3 Comparison of missile displacement and angular displacement at different angles of attack at П=0.2 s(Ma=8)
图10 为5 种攻角下导弹位置变化,表3、图9的数据在图10 的位置变化中体现得更为明显。总而言之,随着攻角的增加,导弹X、Z轴受力和绕X轴方向力矩越大,绕Z轴方向力矩越小。虽然有些工况导弹气动力和气动力矩方向不利于机弹分离,但是在导弹气动力、重力、弹射力的共同作用下,5 种攻角下导弹均能正常投放。正攻角下导弹具有更大的X轴正向位移和Z轴负向角位移,负攻角下导弹具有更大的Z轴负向位移,同时正攻角下导弹X轴方向角位移指向机翼,是机弹分离严重的安全隐患,因而在实际临近空间高超声速飞行器武器投放过程中应避免在正攻角下进行。
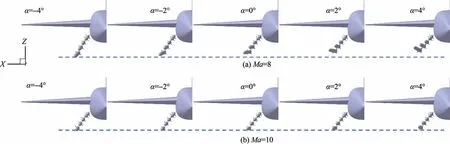
图10 5 种攻角下导弹位置变化Fig.10 Missile position variation at five angles of attack
2.2 飞行高度对导弹投放的影响
飞行高度对导弹投放的影响主要是不同飞行高度的大气密度不同,直接影响机身及导弹的气动力,进而影响导弹投放的姿态变化。随着飞行高度的提升,大气密度降低,相同马赫数下载机和导弹受到的气动力也就越小。对比了Hb=25,30,35 km 的导弹投放,固定飞行马赫数(Ma=8)、载机攻角(α=2°)和导弹初始安装角(θ=0°)。图11 为飞行高度对导弹投放位移和角位移的影响,图12 为不同飞行高度下导弹位置变化对比,表4 为П=0.2 s 时不同飞行高度下导弹位移、角位移对比,可以看出3 种飞行高度下导弹均可以正常投放。当载机在Hb=25 km 高速飞行并进行导弹投放时,导弹具有更大的X轴正向位移和Z轴负向角位移,但是导弹出现了明显的抬头趋势,并且X轴角位移仍直接指向机翼,是载机武器投放严重的安全隐患。П=0.2 s 时Hb=25,30,35 km 在Z轴方向的位移分别为-0.81、-0.81、-0.82 m,不同高度下导弹在Z轴方向的角位移并无明显差别。载机飞行高度由25 km 提升到35 km 并进行武器投放时,X轴正向位移降低了15.79%,绕Z轴负向角位移降低了76.69%。同时,随着高度的提升,导弹抬头趋势逐渐消失,П=0.2 s 时Hb=25,30,35 km 在X轴方向的角位移分别为1.98°、0.98°、-0.09°,不安全的趋势在35 km 时消失,并且此时所有方向位移和角位移都有利于机弹分离。

表4 П=0.2 s时不同飞行高度下导弹位移和角位移对比Table 4 Comparison of missile displacement and angular displacement at different flight altitudes at П=0.2 s
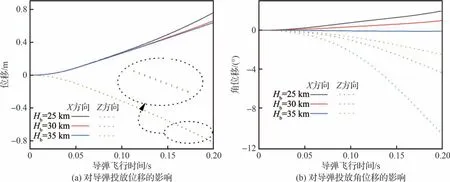
图11 飞行高度对导弹投放位移和角位移的影响Fig.11 Effect of flight altitude on missile separation displacement and angular displacement
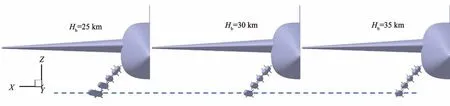
图12 不同飞行高度下导弹位置变化Fig.12 Position variation of missile at different flight altitudes
进一步,分析飞行高度对X轴正向角位移和Z轴负向角位移的影响。由于导弹外挂于机身外,并且位于机头机身过渡段,这使得有些投放规律不同于机身腹部内埋式弹舱武器投放。图13 为机身腹部内埋式武器投放和机身侧面外挂式武器投放示意图,机身腹部内埋式弹舱位于平坦的机身腹部,并且X方向没有其他机构的影响。机身侧面外挂式武器位于机头和机身的过渡段,外部直接是来流大气,内部是机身壁面。因而机身侧面外挂式武器投放在投放初期就受到了X轴正向的气动力作用,有利于导弹和载机分离。
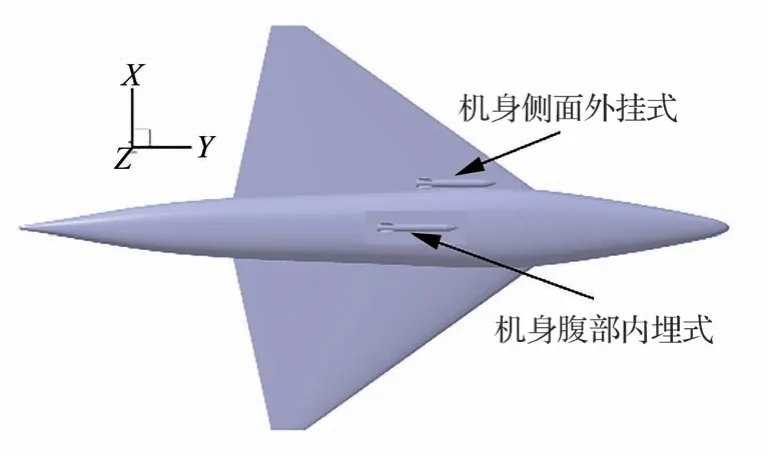
图13 机身腹部内埋式和机身侧面外挂式导弹投放示意图Fig.13 Separation schematic diagram of missile internally embedded in aircraft belly and externally mounted on aircraft side
图14 为不同飞行高度下机身和导弹周围静压云图,可以看出,随着高度的增加,机身和导弹所受静压逐渐降低。这是由于Hb=35 km 的大气压力仅为Hb=25 km 的1/5,并且飞行高度越高,大气密度越低。相同马赫数下动压越小,载机和导弹反而受到更小的气动力作用。也就是说随着飞行高度的增加,机弹分离的气动力和气动力矩减小,导弹投放后的X轴方向位移和绕Z轴方向角位移也相应减小。
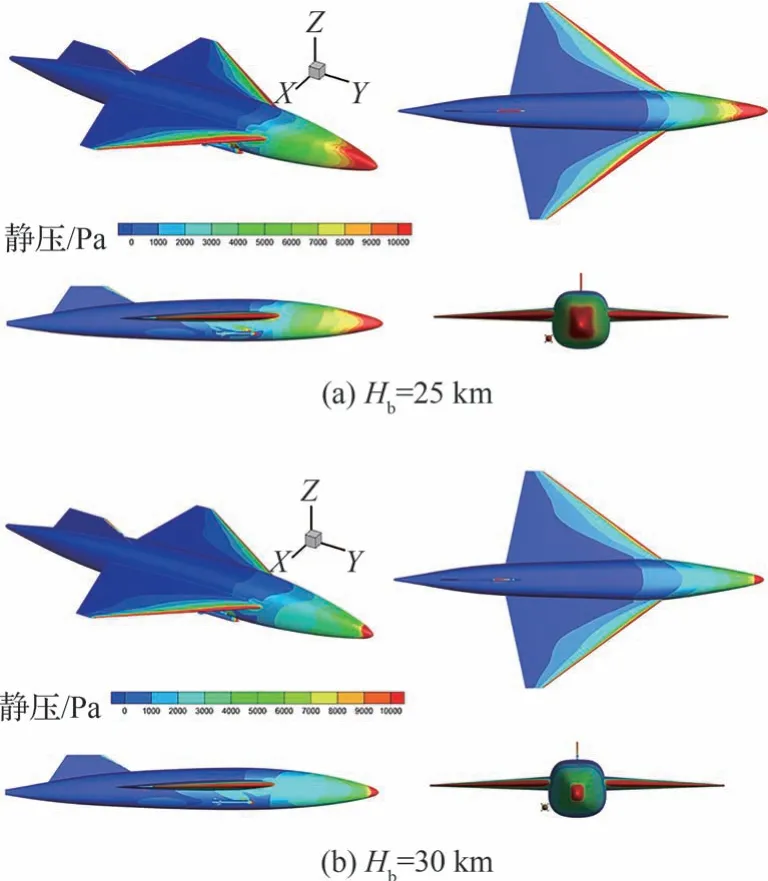
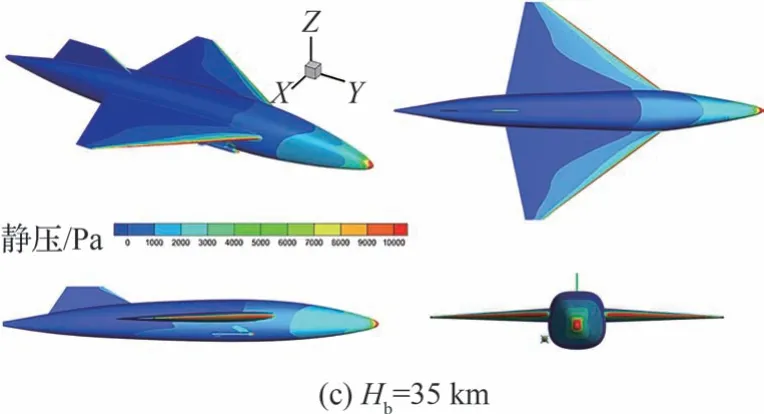
图14 不同飞行高度下机身和导弹周围静压云图Fig.14 Static pressure contour around aircraft and missile at different altitudes
综合导弹投放后位移变化和导弹及机身受力,结论为:随着飞行高度的增加,导弹投放X轴正向角位移和Z轴负向角位移减小。同时,随着飞行高度的增加,导弹的抬头趋势逐渐消失。高度越高,载机和导弹所受气动力越小,更有利于完成机弹分离任务,实际临近空间高超声速飞行器投放过程中建议在Hb=35 km 下进行。
2.3 初始安装角对导弹投放的影响
初始安装角直接影响导弹的气动力和气动力矩,进而影响武器投放的姿态。对比了4 种初始安装角θ=-3°,0°,3°,5°的导弹投放,固定飞行马赫数(Ma=8)、载机攻角(α=2°)和飞行高度(Hb=25 km)。θ=-5°初始安装角的导弹在外伸过程中直接和载机碰撞,故不对θ=-5°及更小的安装角进行讨论。图15 为安装角对导弹投放位移和角位移的影响,表5 为П=0.2 s 时不同安装角下导弹位移和角位移对比,可以看出安装角对导弹位移和角位移都有明显的影响。4 种初始安装角对比,初始安装角θ=-3°时,导弹具有更大的X轴正向位移、Z轴负向位移、X轴负向角位移、Z轴负向角位移,所有姿态参数都占据优势。初始安装角从5°调整为-3°时,X轴正向位移提升了48.39%,Z轴负向位移提升了36.23%,X轴负向角位移提升了1 092.73%,Z轴负向角位移提升了184.24%,各角位移提升显著。并且,θ=5°时X轴方向角位移为6.28°,导弹具有明显的抬头趋势,当初始安装角调整为θ=-3°时,X轴方向角位移为-5.29°,抬头趋势消失。
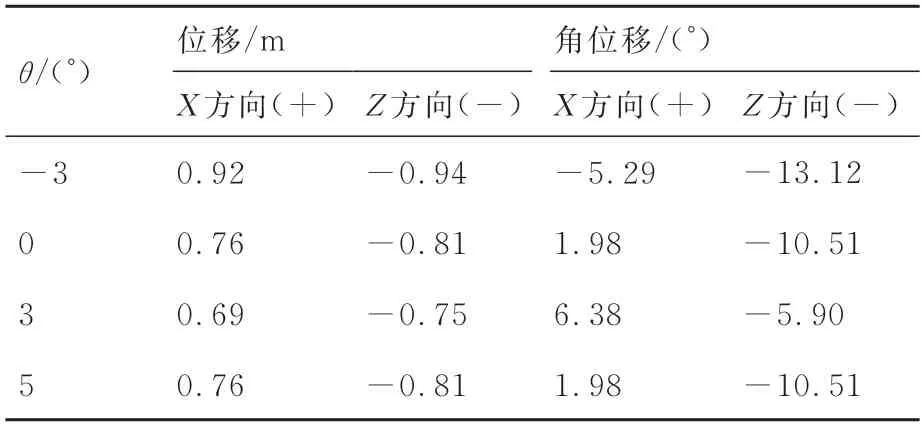
表5 П=0.2 s 时不同安装角下导弹位移和角位移对比Table 5 Comparison of missile displacement and angular displacement at different initial installation angles at П=0.2 s

图15 初始安装角对导弹投放位移和角位移的影响Fig.15 Effect of initial installation angle on missile displacement and angular displacement
图16 为投放初期不同安装角下导弹气动力和气动力矩,可以看出初始安装角θ=-3°时,弹体气动力和气动力矩都有利于机弹分离。正安装角X方向的弹体气动力矩使导弹产生抬头趋势,虽然在弹射力的作用下,导弹依然可以安全分离,但X方向角位移始终是机弹分离的安全隐患。图17 为不同安装角下导弹位置变化,图15、表5 的位移和角位移的变化在图17 中体现得更为明显。由于θ=-3°导弹本身具备X、Z轴负向转角,在导弹投放过程中,受到高速来流的直接作用,θ=-3°具有明显的位移和角位移的优势。因而,临近空间高超声速飞行器武器投放过程,建议在一定负角度的初始安装角下进行。
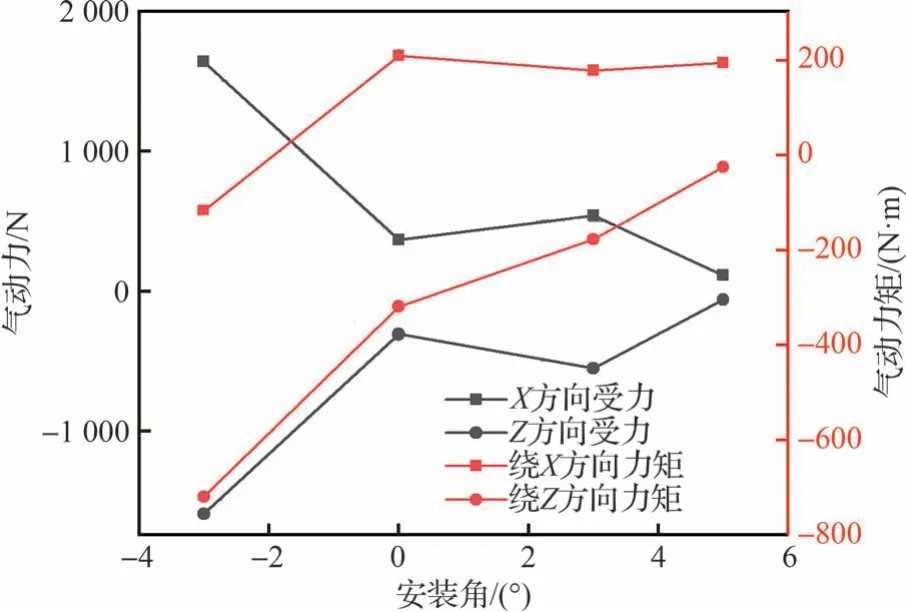
图16 不同安装角下导弹气动力和气动力矩Fig.16 Aerodynamic force and aerodynamic moment of missile at different initial installation angles

图17 不同安装角下导弹位置变化Fig.17 Position variation of missile at different installation angles
2.4 弹射力大小对导弹投放的影响
弹射力是最直接影响导弹投放姿态的因素,固定弹射力作用时间(t=0.05 s)、飞行马赫数(Ma=8)、载机攻角(α=2°)、导弹初始安装角(θ=0°)对比了4 种弹射力F=5,10,15,20 kN 对投放的影响。图18 为不同弹射力大小下导弹位移和角位移变化,表6 为П=0.2 s 导弹位移和角位移的具体数值。可以看出,不同弹射力大小下导弹的位移和角位移变化趋势基本一致。弹射力越大,导弹的X轴正向位移和Z轴负向位移越大。并且,正攻角下导弹具有的抬头趋势随着弹射力的增加而减弱。这是由于弹射力大小远大于气动力,弹射力作用结束后,F=20 kN 弹射力作用下的导弹具有更大的惯性和速度。高速来流对导弹产生的气动力矩对攻角的改变较小,因而导弹绕X轴方向角位移表现为弹射力越大,导弹抬头趋势越小。图19 为4 种弹射力大小下导弹位置变化,可以看出F=5,50 kN 时,导弹最终移动的距离仅为机身直径的2~3 倍,不足以满足临近空间高超声速飞行器武器安全投放的要求。当F=20 kN 时,导弹投放后位移和角位移具有明显的优势。
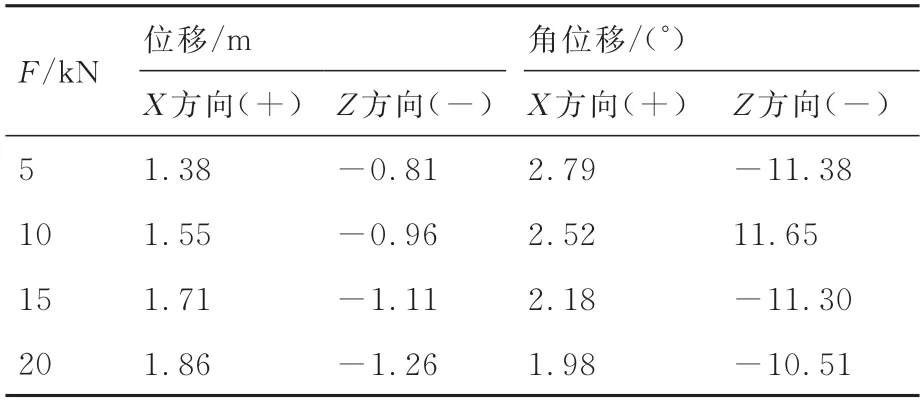
表6 П=0.2 s 时不同弹射力大小下导弹位移和角位移对比Table 6 Comparison of missile displacement and angular displacement at different ejection force magnitude at П=0.2 s

图19 4 种弹射力大小下导弹位置变化Fig.19 Position variation of missile at four force magnitude
另外,考虑到弹射机构的作用距离,当4 种弹射力作用结束时(t=0.05 s),4 种弹射力F=5,10,15,20 kN 下的位移分别为0.04、0.07、0.10、0.13 m。目前导弹弹射大概行程在0.10~0.17 m之间,显然F=15,20 kN 的弹射大小作用下的弹射力作用距离更为合理。并且,弹射力越大,越有利于导弹投放后的姿态越有利于载机和导弹安全。
2.5 弹射力作用时间对导弹投放的影响
除弹射力大小外,弹射力作用时间同样对导弹投放影响显著,固定弹射力大小(F=20 kN)、飞行马赫数(Ma=8)、载机攻角(α=2°)、导弹初始安装角(θ=0°),对比4 种弹射力作用时间t=0.01,0.02,0.05,0.10 s 下对投放的影响。图20 为不同弹射力作用时间下导弹位移和角位移变化,导弹飞行时间П=0.2 s 时t=0.01,0.02,0.05,0.10 s 在Z轴方向的位移分别为-0.33、-0.46、-0.81、-1.25 m,绕X轴方向转角分别为2.72°、2.29°、1.98°、2.54°。弹射力作用时间越长,导弹具有越大的X轴正向和Z轴负向位移,但是作用时间对角位移影响规律不明显。这是由于弹射力大小远大于气动力和重力,导弹主要在弹射力作用下移动,作用时间越长,对导弹姿态控制的效果越大,不同作用时间下导弹角位移变化越小。弹射力作用时间t=0.05 s时,导弹X轴正向角位移最小,对应的导弹抬头趋势最小。
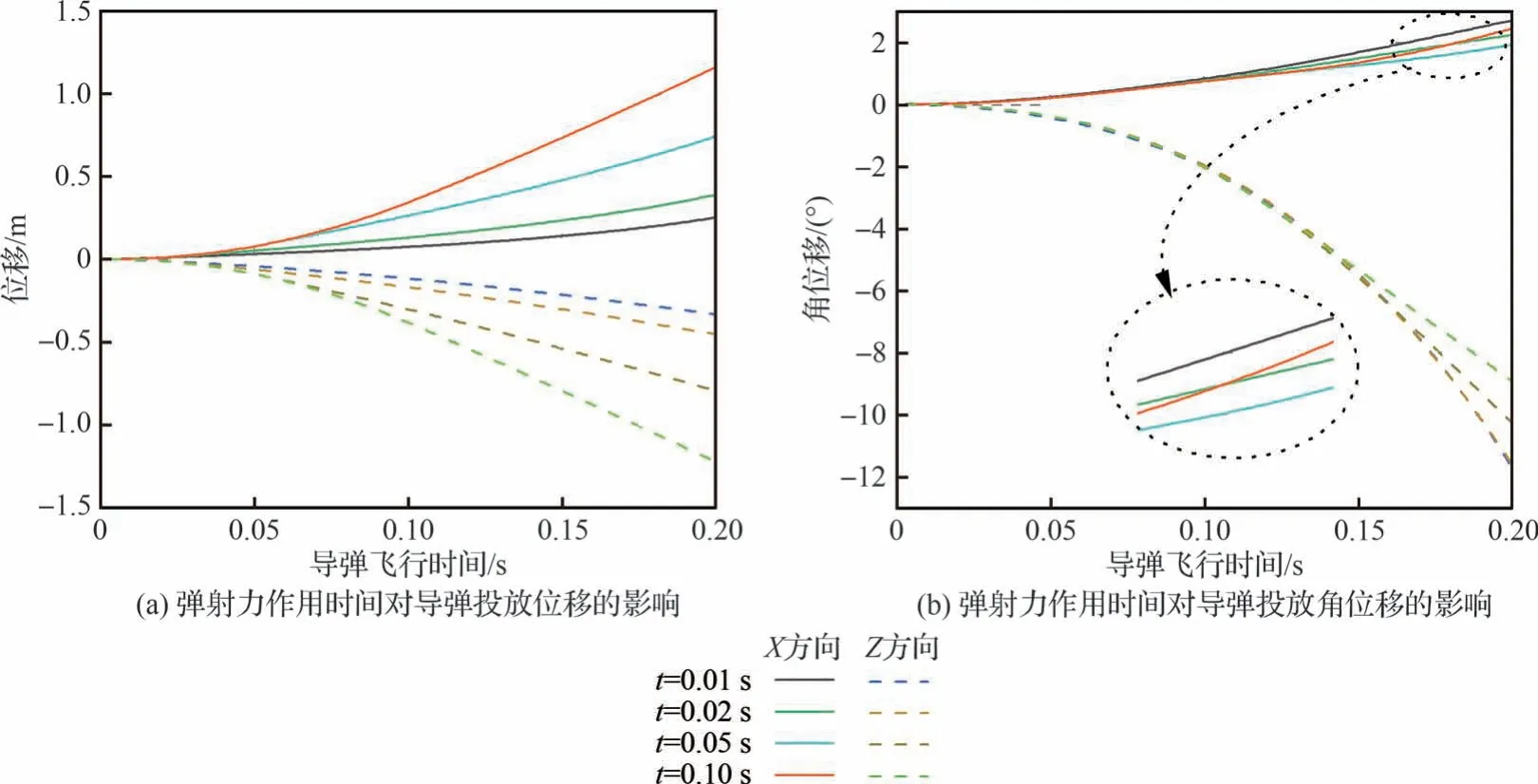
图20 弹射力作用时间对导弹投放位移和角位移的影响Fig.20 Effect of ejection force action time on missile displacement and angular displacement
图21 为4 种弹射力作用时间下导弹位置变化,可以看出,弹射力作用时间越长,导弹Z轴方向具有明显的优势,并且弹射力作用时间t=0.01,0.02 s 的导弹都具有明显的抬头趋势。弹射力作用时间较短时,导弹位移不足以达到武器投放的安全距离。另外,弹射力作用时间为t=0.10 s,弹射力作用结束时(t=0.10 s)导弹位移为0.55 m,超出了弹射机构的最大行程。综合弹射力作用时间对导弹投放位移的影响和弹射机构行程的局限,弹射力作用时间t=0.05 s 是最安全和可行的弹射力方案。

图21 4 种弹射力作用时间下导弹位置变化Fig.21 Position variation of missile at four force action time
3 结论
深入分析了临近空间高超声速飞行器武器投放的可行性,研究了临近空间高超声速飞行器的飞行高度、载机攻角、导弹初始安装角、弹射力大小、弹射力作用时间5 个因素对导弹投放的影响。利用流体-动力学耦合求解方法完成了导弹投放的非定常数值模拟,其中流体计算基于RANS 和SSTk-ω湍流模型。通过对5 种影响因素的研究,包括3 种飞行高度Hb=25,30,35 km、5 种载机攻角α=-4°,-2°,0°,2°,4°、4 种导弹初始安装角θ=-3°,0°,3°,5°、4 种弹射力大小F=5,10,15,20 kN、4 种弹射力作用时间t=0.01,0.02,0.05,0.10 s,得到如下主要结论:
1)攻角对临近空间高超声速飞行器武器投放影响明显,正攻角下导弹具有更大的X正向位移和Z轴负向角位移,但是正攻角下导弹X轴方向角位移指向机翼,是机弹分离严重的安全隐患。当载机由α=4°调整为α=-4°时,X轴方向角位移由5.49°减小到-6.98°,导弹抬头趋势完全消失。因此,负攻角有利于快速和安全地完成机弹分离任务。
2)高度直接影响大气环境,进而影响临近空间高超声速飞行器武器投放。随着高度的增加,相同马赫数下导弹气动力和气动力矩减小。当飞行高度Hb由25 km 提升到35 km 并进行武器投放时,X轴正向位移降低了15.79%,绕Z轴负向角位移降低了76.69%。同时,随着高度的提升,导弹抬头趋势逐渐消失。为了避免导弹投放后的安全隐患,飞行高度Hb=35 km 时导弹位移和角位移都有利于机弹分离。
3)初始安装角对导弹位移和角位移的影响显著。初始安装角θ从5°调整为-3°时,X轴正向位移提升了48.39%,Z轴负向位移提升了36.23%,X轴负向角位移提升了1 092.73%,Z轴负向角位移提升了184.24%,各个角度位移提升显著。同时,θ=5°时导弹具有明显的抬头趋势,当初始安装角调整为θ=-3°时,抬头趋势消失。因而实际进行临近空间高超声速飞行器武器投放时,建议导弹预先调整至一定负角度的初始安装角。
4)弹射力大小和作用时间直接影响导弹投放姿态。弹射力越大、作用时间越长,导弹投放后位移、角位移越大,同时,导弹的抬头趋势也有所减弱。弹射力大小F由5 kN 提升到20 kN 时,导弹X轴正向位移提升34.78%,Z轴负向位移提升55.55%。弹射力作用时间由0.01 s 提升到0.10 s 时,导弹X轴正向位移提升69.22%,Z轴负向位移提升117.35%。但是,较大的弹射力大小和弹射力作用时间会超出弹射机构的行程,实际武器投放过程中难以实现。综合考虑导弹投放后姿态变化和弹射机构能力,建议的弹射力大小F=20 kN,弹射力作用时间t=0.05 s。
临近空间高超声速飞行器武器投放相关研究是航空航天飞行器发展中亟待解决的关键问题之一,对武器分离过程和影响因素的分析不足会导致预测数据出现偏差。在实际机弹分离过程中会导致导弹与载机发生碰撞或产生相互干扰,严重威胁载机及飞行员的安全。因而,临近空间高超声速飞行器研制阶段提出的分离方案和分离影响因素等都十分必要和重要,该项研究可为临近空间高超声速飞行器武器投放可行方案及科学预测提供参考。

