单级跨音压气机第1 级可调静子在退喘过程中的气动力矩分析
刘德龙,郭海宁,尹海宝,孟德君
中国航空发动机集团有限公司 沈阳发动机研究所,沈阳 110015
多级压气机的第1 级具有重要的作用。首先第1 级决定了多级压气机在设计转速附近的流量水平;其次第1 级往往具有最高的压比和进口相对马赫数,在很大程度上还影响了多级压气机的效率水平。另外,为了验证设计思路以及设计参数的合理性,第1 级通常从多级压气机中分离出来单独进行试验。多级压气机为了兼顾非设计转速性能,前面级静子叶片设计成可调的[1-2]。例如在高效节能发动机压气机的方案中[3-4],9 级压气机的前4 排静子可调,10 级压气机的前5 排静子可调。
为了保证第1 级特性与其所在的多级环境下一致,某单级跨音压气机进口导向器(Inlet Guide Vane,IGV)和第1 级静子(the First Stage Stator,S1)也保持为可调静子,如图1 所示。该单级压气机还包括第1 级转子(the First Stage Rotor,R1)、出口导向器(Outlet Guide Vane,OGV)、支板、节气门以及可调静子调节机构。调节机构包括摇臂、联动环、作动筒以及作动筒支架[5-6],如图2所示。在压气机运行时,可调静子叶片(Variable Stator Vane,VSV)始终受到气动力矩的作用,作动筒则产生方向相反的抵抗力矩加以平衡或进行角度调节。本文中的可调静子叶片简称为可调静子。
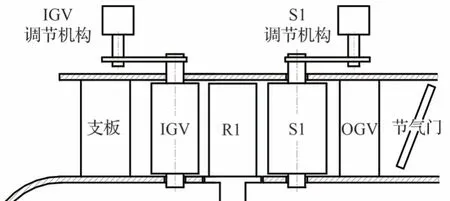
图1 单级压气机布局Fig.1 Single-stage compressor configuration
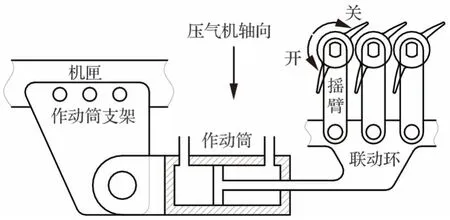
图2 第1 级静子调节机构示意图Fig.2 Schematic diagram of S1 actuation system
该压气机与某高负荷单级压气机[7]具有相同的设计指标,并在相同的试验器上完成了试验,叶片几何及测试布局相似。退喘前后压气机特性轨迹如图3 所示,换算流量和压比分别以堵塞流量和最高压比进行了无量纲化。试验在录取设计转速特性的过程中,在A 点检测到喘振信号后,节气门快速打开,几乎在同一时刻第1 级可调静子瞬间关闭,从摄像头目测指针从设计角度0°向关方向偏转到约23°,如图4 所示。紧接着压气机的换算流量在退喘后1.3 s 下降到最低点,如图3 和图5 中A-B 过程所示。然后压比大幅下降,整个压比下降过程A-D 持续约11 s。发现可调静子关闭后,控制台操纵作动筒希望将其调整到设计角度,在C-D 过程可调静子角度稍有打开,换算流量有所增加,但仍无法回到设计角度,在D-E 过程可调静子角度约为15°。在A-E 过程第1 级转子叶片振幅始终超过安全限制值,为退出该危险状态,压气机转速在E 点开始降低,如图5 所示。在降转过程中可调静子角度恢复到10°。停车后检查发现作动筒支架在推力作用下变形。
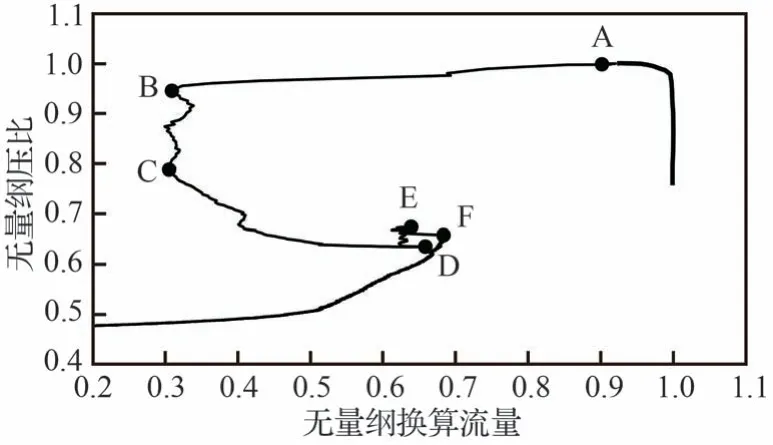
图3 退喘后压气机状态轨迹Fig.3 Path of state of compressor after surge exit

图4 退喘过程中S1 指针变化Fig.4 Variation of S1 needle during surge exit
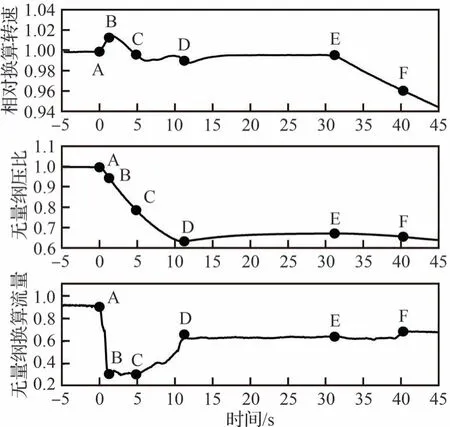
图5 退喘后特征参数随时间的变化Fig.5 Variation of characteristic parameters vs time after surge exit
试验后对整个试验过程进行了回顾:在非设计转速退喘时节气门打开后,第1 级可调静子角度指针也出现了向关角度方向摆动的现象,但摆动较小,还可以通过作动筒再次调整到设计角度,角度开关方向如图2 和图4 所示。
该试验现象在以往的单级压气机文献中没有相关报道。大多数关于单级压气机的文献关注设计方法的验证[8-10]或流动机理的研究[11-14]。由于没有在多级环境下工作的背景,第1 级静子不需要设计成可调的。而在工程实践中为研究多级压气机的进口级特性,带有第1 级可调静子的单级压气机普遍存在。在单级压气机试验过程中第1 级可调静子异常关闭会造成重大损失,因此对其进行受力分析并采取有效措施避免该危险情况再次发生具有重要意义。
从中低转速第1 级可调静子角度指针的变化情况来看,在退喘节气门打开后其受力变化较大。受力主要来自2 方面:首先是受到作用于叶片表面的气动力矩,其次是来源于可调静子调节机构用以平衡气动力矩的抵抗力矩。由于抵抗力矩是根据气动力矩跟随给定的,第1 级可调静子在设计转速退喘瞬间异常关闭的原因定位在气动力矩上。因此本文对气动力矩进行了深入分析。
Mailach[15]和李绍斌[16]等给出了气动力矩的具体算法,本文在可调静子条件下对该算法进行了适应性修改。Aotsuka 等[17]指出,气动力矩的波动主要源于激波在叶片槽道内的运动。本文也分析了激波位置的变化对气动力矩的影响。Rabe 等[18]介绍了转子表面静压的测定方法,进而计算得到转子的气动力矩,这为气动力矩的获得提供了更加直接的测量方法。Sahai 和Cheng[19]从气动力矩的角度介绍了叶型的设计方法,该方法可以推迟叶型吸力面尾缘的分离。毛明明等[20]介绍了掠型转子的设计方法,该方法可以减小下游静子气动力矩的波动。虽然这些文献的研究对象不是可调静子,但为本文气动力矩的分析提供了基础和思路。
可调静子绕其转轴旋转的气动力矩的计算方法与文献[15-16]有所不同。首先把可调静子的转轴而不是叶型重心作为气动力矩的旋转中心,如图6 所示,然后将叶片坐标系的原点也放在气动力矩的旋转中心。那么气动力矩的公式可以写成
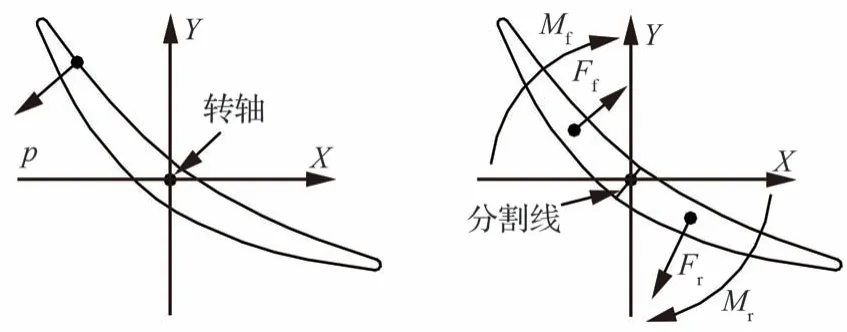
图6 可调静子坐标系下的气动力和相应的力矩Fig.6 Aerodynamic forces and corresponding moments under VSV coordinate system
式中:h为叶片高度;L为叶型型面;p为叶片表面静压。该计算过程由计算机程序完成。为了便于叙述,本文采用如下方法估算气动力矩,整个叶型被通过转轴的虚拟分割线分为前后两个部分,如图6 所示。Ff和Fr分别代表前后两部分叶型所受到的气动力,Mf和Mr分别表示由Ff和Fr所产生的气动力矩,这样整个叶型气动力矩的大小和方向便可以通过Mf和Mr相加估算出来。
本文第1 节采用定常计算给出了气动力矩在压气机特性图上的分布。第2 节采用非定常计算模拟了退喘节气门打开后压气机内部流场及气动力矩的变化情况。第3 节介绍了避免单级压气机第1 级可调静子在退喘过程中异常关闭的措施。第4 节介绍了可调静子可能存在气动力矩过大风险的压气机布局。第5 节给出了结论。
1 定常气动力矩分析
三维计算网格相关信息如表1 所示。计算域采用了O4H 网格拓扑结构,如图7 所示。边界条件进口给定总温和总压,出口给定静压,并通过提高出口静压来调节流量,从而实现从堵塞点到近喘点的模拟。压气机的压比由计算域进口和S1 出口截面的总压计算得到。
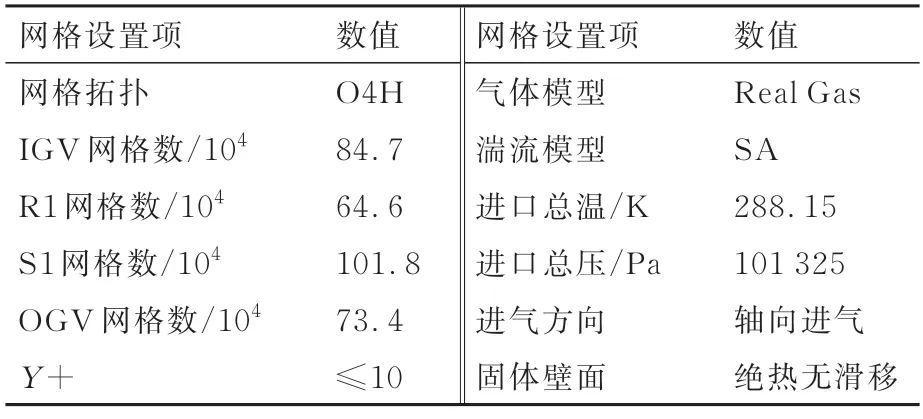
表1 网格及计算设置参数Table 1 Mesh and computation setting parameters

图7 单级压气机计算域及网格Fig.7 Computation domain and mesh of single-stage compressor
设计转速试验和计算特性对比如图8 所示。换算流量、压比和效率分别以试验的堵塞流量,最高压比以及峰值效率进行了无量纲化。特征点的数据对比如表2 所示,可以看出三维计算特性具有足够的精度预测压气机性能。并能很好地反映从堵塞点到峰值效率点,再到近喘点的换算流量变化情况。本节将通过对三维计算典型状态可调静子叶中截面的表面压力分布以及流场的分析,说明试验过程中可调静子沿压气机特性线气动力矩变化的原因。
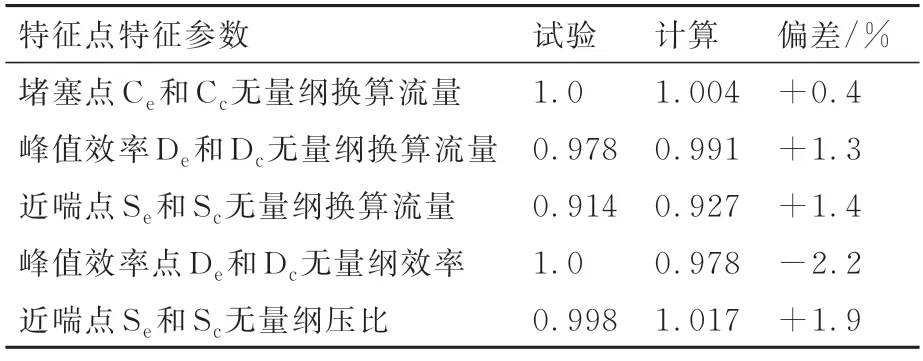
表2 试验和计算数据对比Table 2 Comparison of test and computational data

图8 设计转速试验和计算特性对比Fig.8 Comparison of test and computational performances at design rotational speed
1.1 叶型表面压力分布
在试验过程中,通过调节节气门开度调整压气机工作状态,获取压气机等转速特性线。逐渐关闭节气门,压气机出口压力提高,沿等转速线先后经历堵塞点Ce、峰值效率点De和近喘点Se,如图8 所示。在三维计算中通过提高出口静压模拟这一过程。结果表明,第1 级可调静子在堵塞点Cc、峰值效率点Dc和近喘点Sc这3 个状态受到的气动力矩发生了明显的变化,下文将以叶中截面为例说明整个叶片的工作状态及受力情况。
在堵塞点Cc,叶中截面叶型工作在负攻角状态。此时可调静子吸力面和压力面的静压分布如图9 所示,本节叶型表面压力分布图均以近喘点Sc叶中截面最高静压进行无量纲化。图9 中静压分布线在无量弧长0.4 处相交,以此为分界点前段吸力面压力大于压力面,合力方向由吸力面指向压力面。可调静子转轴位于0.5 无量纲弧长处,所以叶型前段受到关力矩作用;后段则相反合力方向由压力面指向吸力面,但同样产生关力矩。所以整个叶型的合力矩为关力矩,如图10 所示。

图9 堵塞点叶中截面叶型表面压力分布Fig.9 Static pressure distribution on airfoil in middle section of vane at choke point
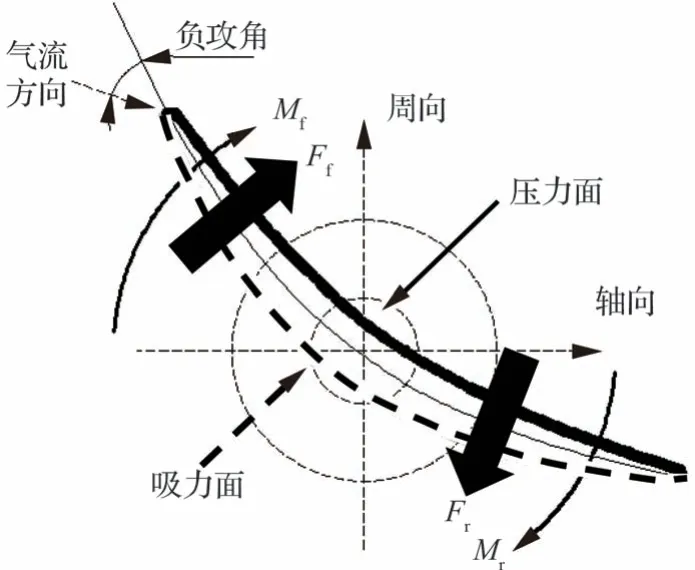
图10 堵塞点叶中截面叶型受力及力矩Fig.10 Forces and moments on airfoil in middle section of vane at choke point
峰值效率点Dc,第1 级可调静子叶中截面工作在零攻角状态,叶型表面静压分布如图11 所示。整个叶型压力面静压大于吸力面,压差力方向由压力面指向吸力面。叶型前段受到开力矩作用,后段为关力矩。由于叶型前段的压差较大,产生的开力矩较大,所以整个叶型受到的合力矩方向为开,如图12 所示。

图11 峰值效率点叶中截面叶型表面压力分布Fig.11 Static pressure distribution on airfoil in middle section of vane at peak efficiency point

图12 峰值效率点叶中截面叶型受力及力矩Fig.12 Forces and moments on airfoil in middle section of vane at peak efficiency point
近喘点Sc,第1 级可调静子叶中截面工作在正攻角状态,叶型表面静压分布如图13 所示。整个叶型压差力方向仍由压力面指向吸力面,叶型前段的压差进一步增加,开力矩进一步增加。叶型后段的关力矩虽然也随着压差的增加而增加,但增加的幅度较小,所以整个叶型受到的合力矩方向仍然为开,且开力矩的幅值增加,如图14 所示。
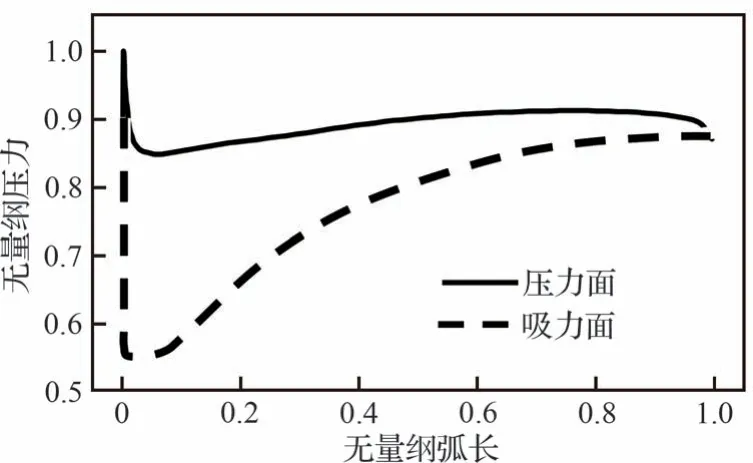
图13 近喘点叶中截面叶型表面压力分布Fig.13 Static pressure distribution on airfoil in middle section of vane at near surge point
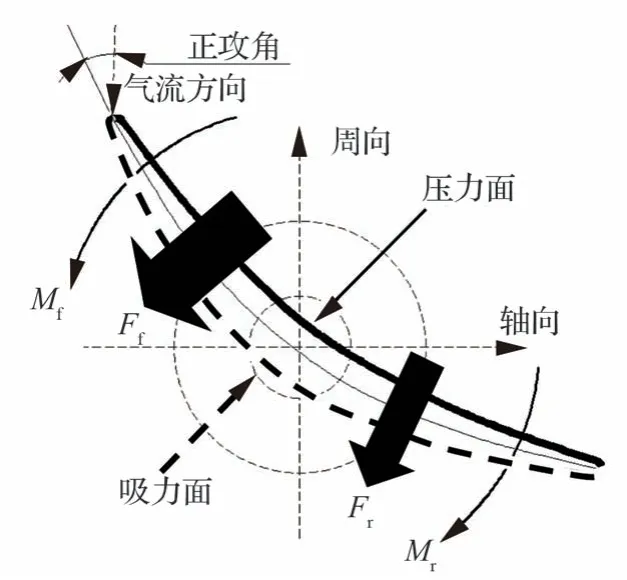
图14 近喘点叶中截面叶型受力及力矩Fig.14 Forces and moments on airfoil in middle section of vane at near surge point
综上,沿等转速线压比升高,压气机工作状态依次经历堵塞点Cc、峰值效率点Dc和近喘点Sc,第1 级可调静子叶中截面依次经历负攻角、零攻角和正攻角,第1 级可调静子受到的气动力矩方向由关到开且变化幅值大。图15 给出了气动力矩沿相对换算转速0.8、0.9、1.0 特性线的分布,压比和换算流量的无量纲方法与图8 相同,可以看出各转速都经历了由关力矩到开力矩的换向过程。

图15 气动力矩在压气机特性图上的分布Fig.15 Aerodynamic moment distribution on performance map of compressor
值得注意的是,由于受到喘振边界的限制,第1 级静子叶片受到的极限开力矩的幅值较小。在1.0 相对换算转速近喘点,整环静子的气动力矩为84 N·m。而堵塞边界尤其在高转速却可以向低压比方向延伸较长,压比越低其所受到的气动关力矩的幅值越大。在1.0 相对换算转速严重堵塞状态,整环静子的气动力矩为-185 N·m。若以该值计算,作动筒支架将受到约2 500 N 的推力。所以高转速低压比的严重堵塞状态构成了试验中的高风险区域,如图15 所示。
1.2 流场分析
在设计转速单级压气机处于严重堵塞的状态点Cc时,不仅第1 级转子,第1 级静子也处于堵塞状态,如图16(a)所示。在转子槽道内有激波Q1,静子槽道内有激波Q2和Q3。随着压气机出口压力的提高,第1 级静子槽道中的激波Q2和Q3向上游移动,并融合为一道激波,如图16(b)所示。直到移出叶栅唇口消失,如图16(c)所示。然后第1 级转子的槽道内激波向唇口移动,直到退出转子唇口,如图16(d)所示。这是该单级压气机沿等转速线流场变化的主要特征。
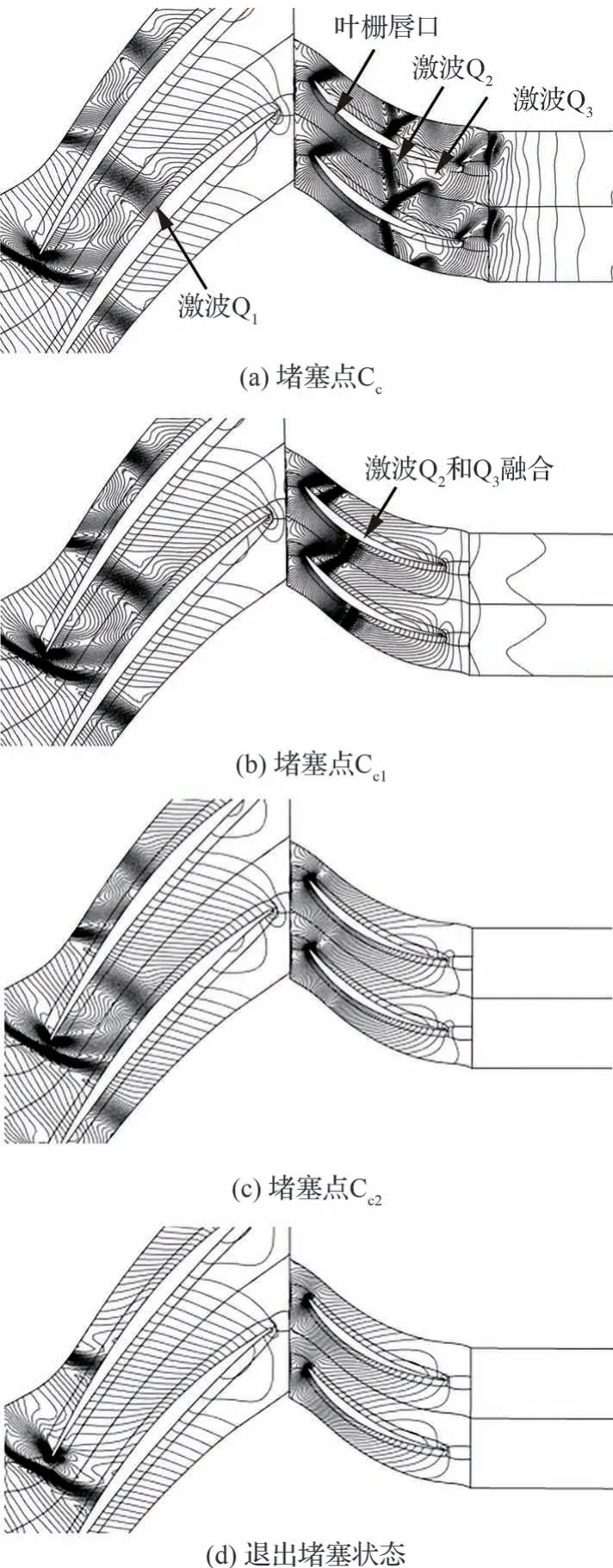
图16 不同出口压力条件下的静压等值线分布图Fig.16 Static pressure contours under different outlet pressure conditions
激波的移动影响着叶片表面压力分布,进而影响第1 级静子的气动力矩。当第1 级静子叶片处于堵塞状态点Cc,激波Q2和Q3位于槽道内时,唇口上游是亚音区域,下游是超音区域,如图16(a)所示。叶型吸力面气流在唇口附近从亚音加速到超音,直到激波Q2。而压力面在激波Q3前气流速度稳定,相应的压力也保持稳定。这就造成了叶型两侧的压力分布呈现交叉的特征,如图17虚线所示。交叉导致叶型前后段的气动力方向相反,而气动力矩的方向相同。这就是静子在堵塞状态相比于峰值效率点Dc和近喘点Sc气动力矩大的原因。

图17 堵塞状态叶中截面静压分布Fig.17 Static pressure distributions along airfoil in middle section under choke conditions
在堵塞状态点Cc,激波Q2和Q3对叶型吸力面和压力面气流起到了减速增压的作用,如图17虚线所示。当出口静压近一步提高,这2 道激波沿叶栅槽道向上游移动并融合为一道激波,在Cc1状态其叶型表面压力分布如图17 实线所示。叶型表面增压过程提前到叶型前半段,在0.17~0.5 无量纲弧长范围产生了较大的开力矩,这使得整个叶型的关力矩减小。所以在静子堵塞状态,压气机压比越高,关气动力矩的幅值越小。
2 非定常气动力矩分析
试验过程中第1 级可调静子在退喘过程中的瞬间关闭表明其必然受到一股强大的作用力。从定常计算中的气动力矩分布来看,只有在堵塞状态的气动力矩无论在方向还是幅值方面都符合条件。而在退喘过程中节气门打开也会将压气机的状态退到低出口静压的堵塞状态。所以采用非定常三维计算捕捉节气门打开后的压气机内部流场的变化情况,并找到可调静子异常关闭的驱动力。需要说明的是,该驱动力必然出现在可调静子关闭之前,所以计算中没有考虑可调静子关闭的动作,而仍保持原有的角度状态。
在计算设置方面,非定常计算与定常计算的主要区别如下:
1)网格周期性:首先对叶片数进行了调整,使转静子交界面有相同的周期,如表3 所示。这样仅对第1 级静子S1 的2 个通道进行网格划分,其余叶排均进行单通道网格划分。叶片数调整前后的定常计算特性对比如图18 所示,图中方形包围的状态点具有相同的出口静压。可以看出叶片数调整后仅近喘点的换算流量稍有增加,但总体还是沿着叶片数调整前的特性线分布。

表3 叶片数对比Table 3 Comparison of blade numbers
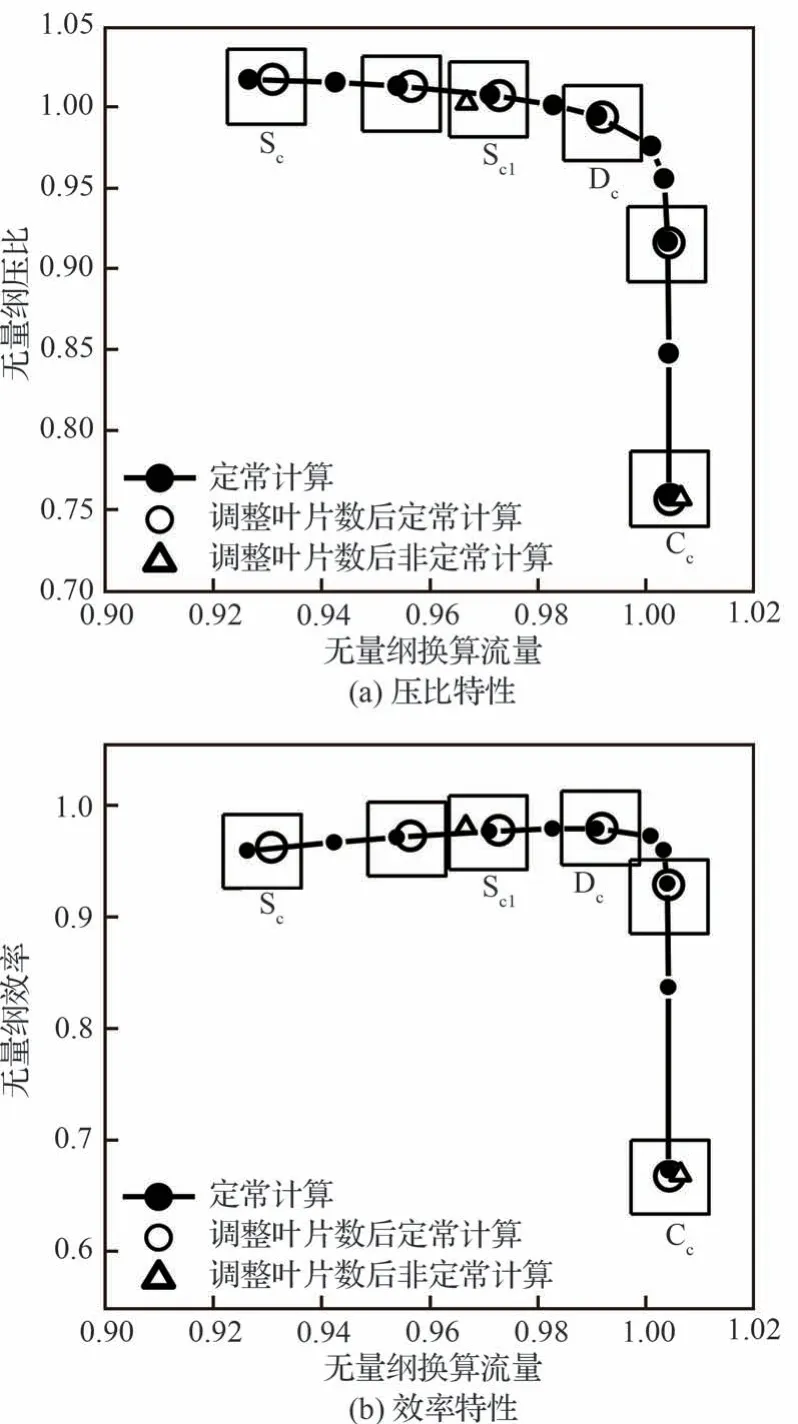
图18 定常与非定常计算特性对比Fig.18 Comparison of steady and unsteady computational performance
2)时间步长:设置一个栅距周期的时间步数ns,根据压气机转速n(r/min)以及叶片数nb确定非定常计算的时间步长ts(s):
3)出口边界条件:通过给定出口静压随时间的间断下降来模拟退喘时节气门快速打开所带来的压气机状态的变化。首先采用恒定的出口静压得到非定常计算的收敛解,如图18 所示。需要说明的是,在非定常计算中近喘点Sc计算不收敛,Sc1是收敛的最高出口静压状态。在给定出口静压随时间的变化时分别以Sc1和Cc状态的出口静压模拟节气门打开前后的出口边界条件。
2.1 流场及叶表压力分布
在非定常计算结果中,由于第1 级转静子存在周向的相对位置变化,压气机进口换算流量、压比以及第1 级可调静子气动力矩随时间也呈现周期性变化,如图19 所示。其中压比和换算流量的无量纲方法与图8 相同。下面以第1 级可调静子叶中截面的流场及叶表压力分布为例说明出口静压突降后气动力矩随时间的变化。在t≤0 ms,为近喘点Sc1状态的一个栅距周期,此时仅在转子唇口上游存在弓形激波,转子和静子槽道内均没有激波,如图20(a)所示。

图19 非定常计算特征参数随时间的变化Fig.19 Variation of characteristic parameters vs time in unsteady computation

图20 非定常计算叶中截面静压等值线及叶表压力分布Fig.20 Static pressure contours in middle section and pressure distributions along airfoil in unsteady computation
在P1状态t=0.014 ms,出口静压下降到堵塞点Cc状态出口静压。如图20(b)所示,计算域出口附近静压等值线密集。此时第1 级静子攻角处于较大的正攻角,叶表静压分布呈现开口状态,整环第1级静子气动力矩约为77 N·m,开方向。
在P2状态t=0.361 ms,如图20(c)所示,密集的静压等值线传到OGV 槽道内,但出口静压的下降已影响到第1 级静子尾缘。尾缘附近的静压下降,前缘附近叶型两侧的静压差减小,压气机的压比也开始下降,如图19 所示。
在P3状态t=0.940 ms,如图20(d)所示,密集的静压等值线传到第1 级静子尾缘附近,尾缘附近静压大幅下降,静子叶片的气动力矩开始下降,此时整环第1 级静子的气动力矩约为56 N·m。
在P4状态t=1.374 ms,如图20(e)所示,密集的静压等值线传到第1 级静子槽道内,槽道内激波已见雏形。叶中截面静压分布已发生重要变化,呈现交叉型的静压分布特征,这说明叶中截面已工作在负攻角状态,此时整环第1 级静子气动力矩约为-58 N·m,气动力矩方向已由开转变为关。
在P5状态t=1.952 ms,如图20(f)所示,静子槽道形成了V 型的2 道激波Q2和Q3。叶中截面交叉型静压分布充分发展,交叉点后移至0.4无量纲弧长位置。此时整环第1 级静子叶片气动力矩进一步下降到-179 N·m。从P3~P5状态共经历约1 ms,气动力矩完成了换向,并达到了非常大的幅值。
在P6状态t=2.386 ms,如图20(g)所示,静子槽道内V 型双激波进一步展开,转子槽道内激波已见雏形。由于静子槽道内激波位置没有发生明显变化,气动力矩也没有发生明显变化,第1 级静子仍受到巨大的关力矩作用。此时压气机进口流量开始显著增加,值得注意的是,压气机进口流量的主要变化发生于静子气动力矩的主要变化之后。
在Cc状态t=4.627 ms,如图20(h)所示,转子槽道内激波Q1和静子槽道内激波Q2和Q3均已成形,形成了稳定的流场结构。压气机进口流量、压比以及第1 级静子气动力矩均呈现稳定的周期性变化。
通过以上非定常计算分析得到以下结论:①压气机出口静压下降后,第1 级可调静子气动力矩会在毫秒级的时间内完成换向,之后始终处在巨大的关力矩作用下;②在压气机进口流量增加之前,第1 级可调静子就已经受到了巨大的关力矩的作用。这说明在试验退喘时节气门打开后,第1 级可调静子在压气机进口流量变化之前,便在巨大的关气动力矩作用下关闭,取代节气门成为新的节流位置,导致压气机进口流量下降。所以在退喘后的压气机的流量是向小流量方向变化,如图3 中A-B 过程所示,而不是向大流量方向的堵塞点变化。
2.2 退喘过程回顾
在退喘前可调静子受到开方向的气动力矩作用,此时作动筒提供了幅值相当方向相反的关力矩以保持可调静子角度稳定。检测到喘振信号时,如图3 中A 点所示,节气门迅速打开,可调静子瞬间进入严重堵塞状态,气动力矩在极短的时间内由开力矩转变为幅值巨大的关力矩。巨大的关力矩使可调静子从0°迅速关闭约23°,并推动作动筒导致作动筒支架变形。此时第1 级可调静子取代节气门成为新的节流位置,压气机流量进一步减小,如图3 中A-B 过程所示。为恢复可调静子角度控制台通过作动筒进行调整,但仅能够调整到15°,换算流量有所增加,如图3 中C-D过程所示。在A-E 过程转子振幅始终超过安全限制值,为退出该危险状态紧急降转。在降转过程中由于气动力矩的卸载,可调静子角度恢复到10°。但由于作动筒支架变形,调节机构的行程受限,可调静子无法恢复到设计角度0°。
3 预防措施
为保证具有第1 级可调静子的单级跨音压气机的试验安全,采取了以下预防措施:
1)对可调静子调节机构进行强度校核。整个机构应具有足够的强度和刚度能够承受全工况范围的最大气动力矩,最大气动力矩位于高转速的堵塞状态。
2)试验过程中监控可调静子受到的气动力矩幅值。可调静子的气动力矩通过作动筒力进行监控,作动筒力根据作动筒两侧腔压计算得到。
3)通过节气门开度控制可调静子气动力矩。在磨合试车阶段定位气动力矩大的高风险区域并记录相应的节气门开度。在退喘时应控制节气门开度,避免压气机进入严重堵塞状态,使第1级可调静子承受巨大的气动关力矩。
以上预防措施在后续单级压气机[7]的试验中进行了验证,结果表明是有效的。由作动筒产生的作用在可调静子上的抵抗力矩可以通过计算得到:
式中:F是作动筒产生的力;La是该作用力的力臂,当摇臂与联动环垂直时,其等于摇臂的长度;Na是作动筒的数量。
试验前采用三维计算获得第一级可调静子的气动力矩分布,气动力矩大的状态位于高转速的堵塞状态。在特性线的最低压比点气动力矩达到-189 N·m,如图21 所示。其中的压比和换算流量分别以试验特性的最高压比和最大换算流量进行了无量纲化。磨合试车阶段根据计算结果以及作动筒力的监控定位气动力矩大的三角区域,如虚线以下区域所示,该区域作动筒力矩超过200 N·m。然后通过控制节气门在虚线上方区域完成特性录取以及退喘操作,退喘后作动筒力矩为-107 N·m,没有发生第1 级可调静子异常关闭的现象,压气机状态由喘振状态成功退到较大流量的堵塞状态。验证了预防措施的有效性,同时也排除了喘振导致可调静子异常关闭的可能。

图21 作动筒力矩及计算气动力矩Fig.21 Moments produced by actuators and aerodynamic moments from computations
图21 给出了由计算得到的可调静子气动力矩和由试验得到的作动筒力矩的对比。可以看出,在特性线大流量范围计算的气动力矩和作动筒力矩结果符合较好。在近喘点附近,计算的流量较小且存在气动力矩换向的现象,而作动筒力矩均为关方向,但变化趋势与计算相符。作动筒力矩验证了定常三维计算中第1 级可调静子气动力矩沿等转速线的分布规律以及气动力矩大的高风险区域。
4 气动布局
可调静子是否会受到巨大的气动力矩还与压气机布局有关。下游的节气门对多级压气机各级工作点的影响从后向前是逐级递减的,各级可调静子气动力矩的变化幅度也相应逐级递减。所以可调静子不出现在后面级尤其是末级,其气动力矩在堵塞状态以及沿等转速线的变化很小。
在多涵道压缩系统中,如果压缩部件的可调静子布置在外涵前[21],如图22 所示,其状态直接受到外涵道出口压力的影响。在调节外涵流量的过程中,该位置可调静子的气动力矩也可能有较大的变化或工作在较大的气动力矩状态下。应进行可调静子的气动力矩评估以及相应调节机构的强度校核。
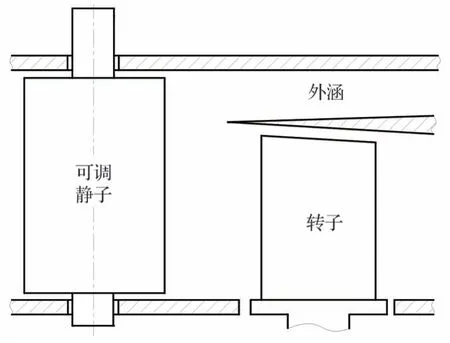
图22 可调静子在外涵道前的布局Fig.22 Configuration of VSV just in front of bypass
5 结论
为找出单级跨音压气机第1 级可调静子在设计转速退喘过程中异常关闭的原因,采用三维计算对第1 级可调静子的气动力矩进行了分析。结果表明,可调静子的气动力矩直接受到节气门开度的影响:
1)在高转速如果节气门完全打开,单级压气机将工作在严重的堵塞状态,第1 级可调静子承受巨大的关力矩。
2)随着节气门的关闭,压气机压比沿等转速线上升,攻角由负转正,叶型表面压力由交叉型转变为开口型,气动力矩由关力矩转变为开力矩。
3)在设计转速退喘过程中第1 级可调静子异常关闭的原因是:节气门打开过大使压气机进入到严重堵塞状态,第1 级可调静子在巨大的关气动力矩作用下关闭。
4)为防止该异常情况再次发生,本文介绍的预防措施包括:试验前对可调静子调节机构进行强度校核,试验中通过作动筒腔压监控可调静子气动力矩,磨合试车阶段对气动力矩大的高风险区域进行定位,以及退喘过程中控制节气门的开度等。后续的单级跨音压气机的试验情况表明,这些措施可以避免第1 级可调静子在退喘过程中异常关闭,保障试验安全。

