考虑供应中断时间的两级汽车供应链优化与恢复策略

卢志平，玉晓晶

（1.广西科技大学 经济与管理学院，广西 柳州 545006；2.广西高校智慧物流与供应链管理重点实验室，广西 柳州 545006）

党的二十大报告指出，着力提升产业链供应链韧性和安全水平。这对于维护我国经济安全和推动高质量发展，具有重大战略意义。[1]汽车供应链是一个由原材料及零部件供应商、整车制造商和产品分销商构成的网络体系，其中任何环节出现问题都可能导致供应链断链危机。近年来，全球汽车制造供应链受缺芯、原材料涨价、自然灾害频发和国际局势变化等多重因素的影响，供应链风险不断上升，许多汽车企业因为供应链问题而不得不减产或停产。汽车供应链的复杂性和脆弱性使其更容易受到各种因素的干扰，如物流效率降低、运输时间不可控等。面对外部不确定因素的冲击和影响，企业和管理者认识到了供应链弹性的重要性，并将提高供应链弹性作为主动管理和降低供应中断风险的一种方式。

供应链弹性策略研究是供应链中断风险管理研究领域的重要内容之一。供应链弹性概念最早由Rice 提出，其认为供应链弹性是指供应链对各种意外中断作出反应并恢复到正常供应网络运营的能力[2]。Sheffi 等[3]从供应链企业的角度出发，将供应链弹性解释为企业吸收中断的能力，使供应链网络更快地恢复到原状态条件，对企业业绩产生了积极的影响。目前，学界涉及供应链弹性策略研究的文献众多，既有研究从不同的角度提出了供应链弹性策略，对突发事件引起的供应中断问题展开了深入研究。Thomas 等[4]认为，与供应商建立牢固的供应商关系，可以使供应链更具有弹性。Demirel 等[5]建议采取灵活采购、备用供应商的策略，以减少供应中断。Ivanov[6-7]提出了应急采购、备用供应商、双重和多重采购等策略，以提高供应链弹性。Razavian 等[8]提出了与后备或替代供应商以及与多个采购方签订合同策略。Salama[9]等提出了后备分包商和备用采购策略。关志民[10]等提出采用多元采购策略，并综合考虑弹性供应链成本与服务水平。此外，部分学者提出了现货采购策略、构建云制造供应链网络[11-12]。综上所述，备用供应商策略是提高供应链弹性的一种重要策略。鉴于突发事件具有不确定性和不可预测性的特点，本文采取临时采购策略，认为在突发事件发生时，除了要启动备用供应商策略，同时还要通过市场进行临时采购以确保恢复正常供应。

供应链弹性研究方法种类众多，其中数学建模是供应链弹性研究中使用最广泛的一种方法。Sawik[13]针对大流行中断引起的多区域供应链随机优化问题，采用了随机混合整数规划模型，解决了区域中断风险带来的连锁反应下供应链运营优化问题。闫妍等[14]针对6 层供应链网络节点失效问题，建立了总成本最小化的混合整数线性规划模型，解决了有限资源能力约束的应急调度问题。马为民等[15]为设计一个可靠的供应链网络，同时考虑了三级供应链节点中断和需求不确定的情况，结合p-鲁棒模型建立了一个新的混合整数线性规划模型。肖建华等[16]研究了供应网络多层级节点失效、需求波动问题，构建了弹性供应链网络的优化模型。高聪等[17]针对分销中心因发生失效事件而不能接受制造商供货的问题，提出了考虑供应恢复失效的混合整数规划模型，解决了分销中心转运时间恢复时效不确定的问题。任慧[18]在设计可靠的弹性供应链网络时，考虑供应链网络中的运输中断风险，建立了以总运营成本最小化和运输可靠性最大化为目标的混合整数规划模型。李珍萍等[19]针对供应网络中主供应商或运输路径中断的问题，采用两阶段随机规划模型，并将其转化为混合整数线性规划模型进行求解，有效地解决了在节点和运输路径同时中断时弹性供应链网络设计的问题。杨毅[20]针对三级供应链中断问题，采用混合整数规划模型，解决了中断情况下同时考虑制造商利润和顾客满意度的供应链恢复决策问题。Chen 等[21]针对新冠疫情造成的供应商在供应中断后无法在短期内恢复的问题[21]，采用混合整数线性规划模型，解决了制造商在短期内恢复困难的问题，有效地减少了制造商由于供应链的特殊中断而造成的经济损失。当前，供应链弹性领域研究成果丰硕，混合整数规划模型已在供应链弹性研究中得到广泛的应用。然而，已有研究大多数聚焦于供应链网络节点中断和需求不确定，鲜有研究对供应中断的时间进行深入研究，特别是考虑供应商短期、长期中断的研究相对较少。考虑到突发事件频繁发生的可能性，本文从中断时间的维度对供应链弹性进行研究具有重要的现实意义。

本文以供应商、整车制造商组成的二级供应链为研究对象，考虑供应商不中断、短期中断、长期中断3 种情况，对突发事件造成的供应中断问题进行研究。在中断时考虑备用供应商和临时购买两种策略，以提高供应链弹性。以制造商的总成本最小化为目标，建立供应中断问题的混合整数线性规划模型，并采用Gurobi 求解器得到最优采购方案和最优组合策略，最后通过算例分析和敏感性分析验证模型的可行性和有效性，以期为决策者应对供应中断问题提供相关管理启示。

一、问题描述与假设

（一）问题描述

本文考虑由供应商、整车制造商组成的二级汽车供应链。突发事件发生时，供应商i可能面临不中断、短期中断、长期中断3 种情况。其中，未中断的供应商能够正常供应；发生短期中断的供应商，待其恢复后可以继续供应，但其供应能力有所损失；长期中断的供应商，无法供应。当突发事件发生时，若制造商不及时采取任何恢复供应的措施，可能导致制造商要付出相应的缺货成本。为了减少制造商的损失，本文采取如下措施：向未中断的供应商继续采购；对于发生短期中断的供应商或长期中断的供应商，制造商可选择启用备用供应商或临时购买的策略。

（二）问题假设

为了更好地研究弹性供应链优化模型，本文提出如下假设：

H1：每个供应商只能选择一种中断状态，且各供应商之间的中断相互独立，只与该地区存在的突发事件有关。

H2：各生产基地的需求量已知，不会因突发事件而发生变化，且各生产基地的临时购买成本和缺货成本为常数。

H3：原始供应商的固定订单成本已知，采购成本和运输成本是常数。

H4：备用供应商相互独立且不会发生中断，其采购成本和运输成本为常数。

二、模型构建与求解

（一）参数设置

研究模型涉及的集合、索引和参数以及决策变量分别如表1、表2 所示。

表1 模型参数

表2 决策变量

（二）模型建立

衡量供应链弹性能力的标准之一是制造商在面临突发事件时的成本损失值，为设计弹性供应链，制造商通常以实现成本最小化或利润最大化为目标[22-23]。为此，以制造商总成本最小化为目标函数，分别建立正常情况下和中断情况下的数学模型。

正常情况下的数学模型：

其中，式（1）为正常情况下的目标函数，表示原始供应商的固定订单成本、原材料采购成本和运输成本的最小化；式（2）表示每个供应商提供的原材料量不能超过其最大的供应量；式（3）表示每个生产基地原材料的需求量都得到满足；式（4）表示所有的决策变量都是非负的。

当发生供应中断时，如果考虑采取备用供应商策略，制造商需支付额外的成本，包括备用供应商的固定订单成本、采购成本和运输成本。同样，如果考虑采取临时购买策略，制造商的总成本还包括从市场临时购买原材料的采购成本和运输成本。此时，目标函数主要涉及的成本有固定订单成本、采购成本、运输成本和缺货成本。

1.固定订单成本。固定订单成本，是指制造商向供应商下订单时产生的成本，无论订单的大小和如何变化，固定订单成本通常都是恒定的。当制造商从多个供应商订购原材料时，总固定订单成本等于所有供应商的固定订单成本之和。当突发事件发生时，若制造商采取备用供应商策略，需要向被选中的备用供应商支付相应的固定订单成本。此时，总固定订单成本为F1。

2.采购成本。采购成本等于原材料的单位采购成本乘以采购的原材料量。正常情况下，制造商的采购成本等于供应商i购买的原材料单位采购成本乘以采购量之和。当突发事件发生时，制造商的采购成本主要包括4 部分：向未中断的原始供应商采购原材料的成本、向短期中断的原始供应商采购原材料的成本、向备用供应商采购原材料的成本以及从市场临时购买原材料的成本。此时，总采购成本为F2。

3.运输成本。运输成本等于原材料的单位运输成本乘以采购的原材料量。当突发事件发生时，制造商的运输成本主要包括未中断的原始供应商的运输成本、短期中断的原始供应商的运输成本、备用供应商的运输成本以及从市场临时购买的运输成本。此时，总运输成本为F3。

4.缺货成本。缺货成本等于单位缺货成本乘以缺货量。缺货量等于每个生产基地的原材料需求量减去原材料采购量的总和。因此，总缺货成本F4等于所有生产基地的缺货成本的总和。

综上，建立供应中断情景下的数学模型：

可见，供应中断情景下的数学模型是一个混合整数线性规划模型。其中，式（9）表示当发生供应中断时，以制造商采取弹性策略后产生的总成本最小化为目标函数。式（10）表示未中断的原始供应商提供的原材料量不能超过其最大供应量。式（11）表示面临短期中断的供应商提供的原材料量不能超过其最大供应量。值得注意的是，由于受到突发事件的影响，面临短期中断的供应商的最大供应能力变为（1-αi）Ui。式（12）表示生产基地j向备用供应商n采购的原材料量不能超过备用供应商的最大供应能力。式（13）表示未中断的供应商、短期中断的供应商、备用供应商提供的原材料以及临时购买的原材料量与缺货量之和恰好等于生产基地j的需求量。式（14）、式（15）表示在突发事件发生时，每个供应商只能选择一种状态。式（16）规定了决策变量的取值范围。式（17）、式（18）表示变量为二元变量。

（三）求解步骤和算法说明

为求解供应中断下的弹性供应链优化模型[24-26]，利用python 3.9 编程设计求解该模型的算法，整体思路如下：

Step1 定义数学模型的目标函数和约束，并将其添加到Gurobi 求解器中。

Step2 输入已知的模型参数值，模型初始化。

Step3 使用Gurobi 求解器求解正常情况下的MILP 模型。

Step4 随机确定并模拟突发事件发生时原始供应商的状态。

Step5 求解中断情形下不采取策略、采取单一策略、组合策略时的MILP 模型。

Step6 对模型的关键参数进行敏感性分析。

三、算例分析

（一）参数设置

本文构建由供应商和整车制造商组成的二级供应链。假设该二级供应链中有6 个供应商，整车制造商具有12 个生产基地，每个供应商都可以向生产基地提供原材料。当出现供应中断时，有3个备用供应商可供整车制造商选择。

为体现参数设置的科学性，参考相关文献[27-29]，在合理区间内随机生成算例的各项参数。原始供应商的相关参数如表3 所示，备用供应商的相关参数如表4 所示，各生产基地的原材料需求量如表5 所示。此外，从市场临时购买原材料的成本e=16，运输成本l=6。

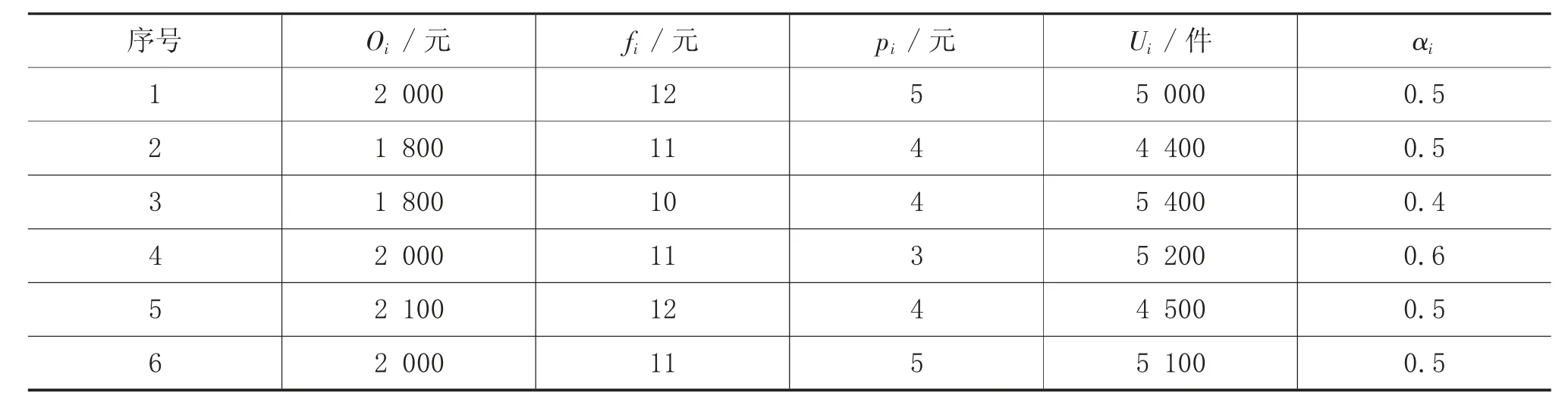
表3 原始供应商参数

表4 备用供应商参数

表5 生产基地的原材料需求量

（二）计算结果分析

根据表3 和表5 的数据，基于pycharm 平台运行代码，计算正常情况下的最优采购方案，结果如表6 所示。

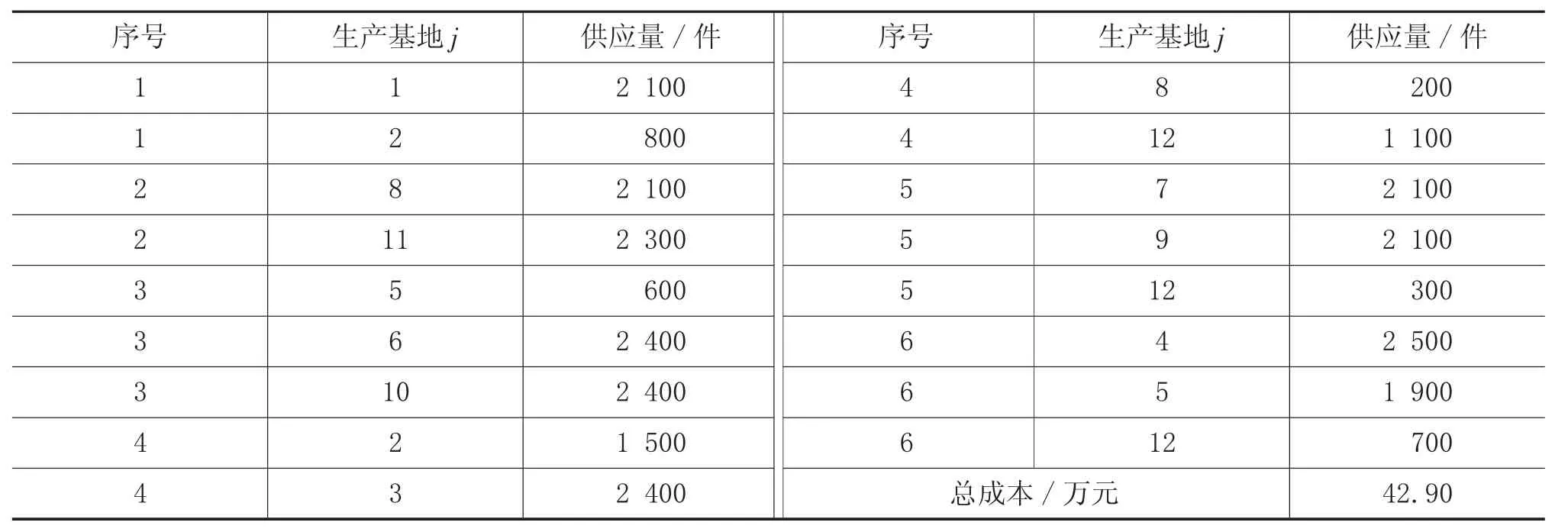
表6 正常情况下制造商的最优采购方案和总成本

当突发事件发生时，供应商面临不同类型的中断，若制造商不打算采取任何策略，只从未中断的供应商和经历了短期中断的供应商购买原材料。同时考虑存在不中断、短期中断和长期中断的供应商，在考虑供应中断时间情形下分析制造商不采取任何措施时花费的最小总成本。当突发事件发生时，假设不中断的供应商数量、面临短期中断的供应商以及面临长期中断的供应商数量均为2。为确保供应商在突发事件发生时，不中断、面临短期中断和面临长期中断的概率是相同的，使用random.sample 函数随机设置每个供应商的状态（表7）。制造商不采取任何策略时，最优采购方案如表8 所示。

表7 突发事件发生时供应商的状态

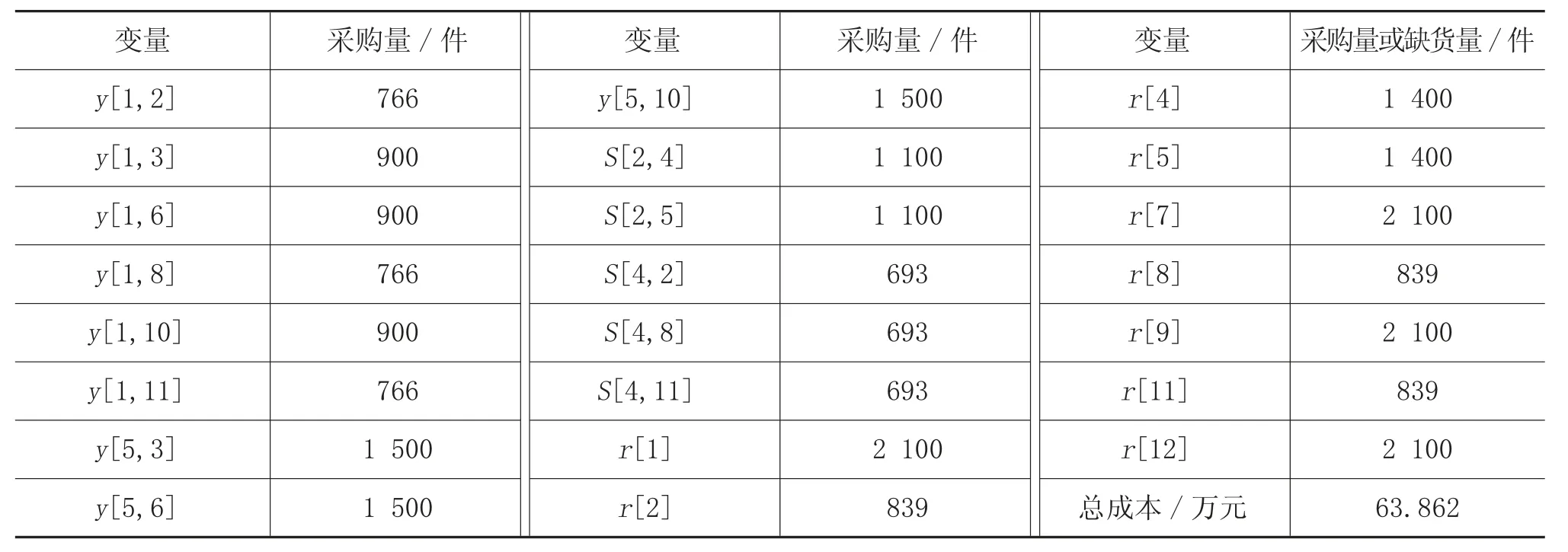
表8 制造商未采取任何策略时的最优采购方案和总成本

由表8 可以看出，虽然制造商继续向未中断的供应商和短期中断的供应商采购原材料，但未能满足每个生产基地的需求，使每个基地都出现较大的缺货情况。由于原材料面临短缺，导致制造商的总成本大幅增加。因此，制造商有必要采取相应的策略，以降低总成本，构建弹性的供应链。

在相同的供应中断情况下，若制造商选择采取补救措施，可有备用供应商、临时购买策略供其选择。制造商需要根据原始供应商的中断情况以及每个生产基地的需求量，以成本最小化为决策目标选择最优的策略并确定采购的数量。沿用制造商不采取任何策略时每个供应商的状态，制造商采取备用供应商或临时购买策略后的采购方案和总成本如表9 所示。

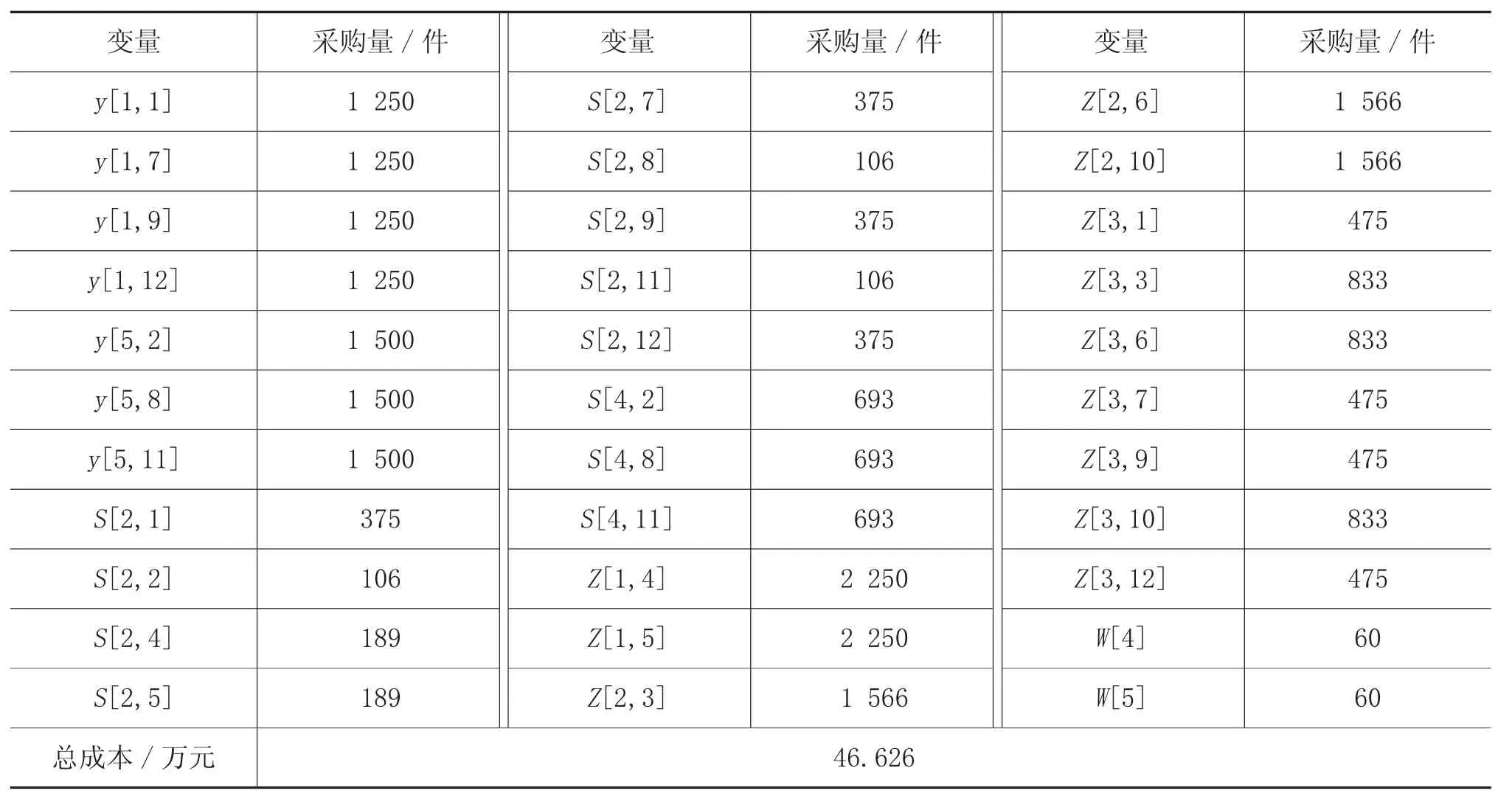
表9 制造商采取弹性策略后的最优采购方案和总成本

综上可知，当供应商1 和供应商5 不中断、供应商2 和供应商4 为短期中断、供应商3 和供应商6 为长期中断时，制造商选择采取备用供应商的策略。通过向3 个备用供应商购买原材料使自己的需求得到满足，无需承担缺货的费用。图1直观展示了供应中断后不采取策略、采取单一策略和组合策略对制造商总成本的影响。

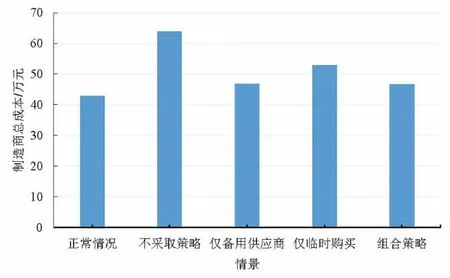
图1 不同情景下的目标函数值

由图1 可知，中断后若不采取策略，制造商将要承担巨大的成本。不论是采取单一策略还是组合策略，制造商需承担的总成本都低于不采取策略时的成本。因此，当突发事件造成供应中断时，制造商应及时采取策略，避免造成成本负担过重。分别将采取组合策略后的总成本、未采取策略的总成本与正常情况下的总成本相比，采取组合策略后制造商总成本的增额明显减少，表明中断后采取组合策略能缓解总成本的增加。

（三）关键参数灵敏度分析

由于中断后供应商的生产能力损失系数、备用供应商的单位采购成本和单位运输成本、临时采购成本等关键参数均会影响制造商的总成本，同时这些关键参数的变化对制造商的采购计划和策略的选择也会产生影响。通过对这些参数进行敏感性分析，可以分析制造商总成本的变化情况。本文在对某一关键参数进行分析时，并不改变其他参数值。关键参数灵敏度分析结果如表10 所示。

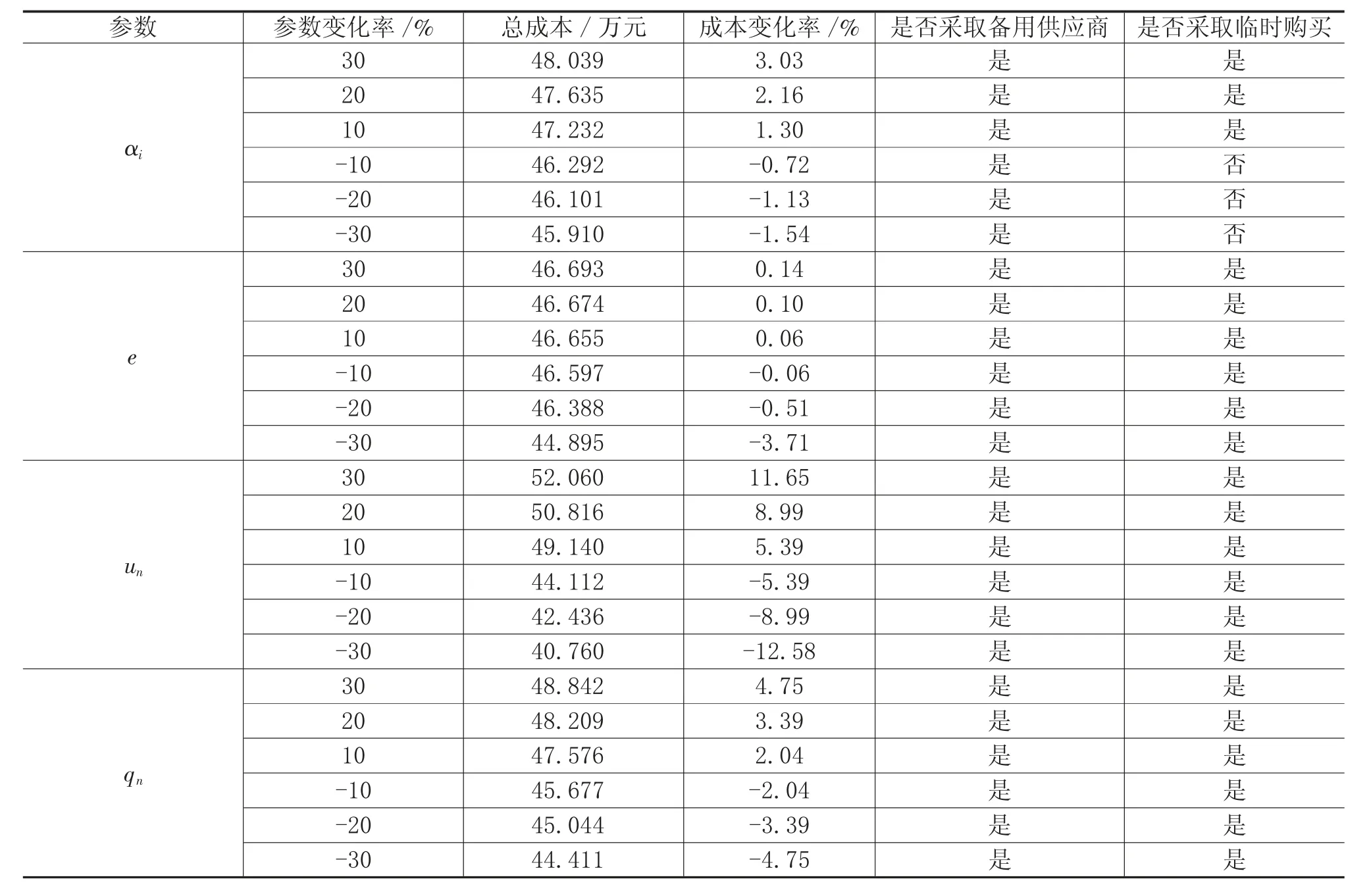
表10 关键参数的灵敏度分析结果

由表10 可知，将参数按照初始值变化±10%、±20%、±30%时，制造商的总成本都发生了相应的变化。参数与制造商的总成本两者的变化趋势相同。当生产能力损失系数、临时购买成本、备用供应商的单位采购成本和运输成本的变化率增加时，制造商的总成本也随之增加。无论参数如何变化，制造商都会选择采取备用供应商，且制造商的总成本变化与参数的变化一致。由此可见，与临时采购相比，备用供应商对制造商总成本的变化发挥着主导的作用。对比数据发现，当生产能力损失系数负向变化时，制造商仅选择备用供应商策略，其余情况下制造商都选择备用供应商和临时购买的组合策略。这表明制造商考虑备用供应商和临时购买组合策略对于减轻突发事件引起的供应中断和构建弹性供应链是可行的。

同时，从表10 可知，当备用供应商的单位采购成本增加30%时，制造商总成本的变化率达到最高，为11.65%。虽然制造商的总成本随着4 个参数变化率的增加而增加，但是增加的幅度有所差别。当备用供应商单位采购成本和运输成本、生产能力损失系数变化率单调递增时，总成本增加的幅度明显较大。对比发现，制造商总成本对备用供应商单位采购成本和临时购买成本参数负变化的敏感度相对更高。当临时购买成本减少20%和30%时，制造商的总成本明显减少；当临时购买成本减少10%和增加10%以上时，虽然会导致制造商的总成本增加，但是增加的幅度不明显，表明此时临时购买对缓解制造商总成本增加作用不明显。

（四）不同供应商中断数量下制造商的总成本与弹性策略的敏感性分析

为进一步了解由突发事件引起的不同供应商中断对制造商总成本的影响[30-32]，通过改变不中断供应商集合，短期中断供应商集合、长期中断供应商集合的数量，分析制造商总成本的变化情况。考虑到直接确定供应商状态会引入主观因素从而导致结果产生偏差，仍使用random.sample 函数随机分配供应商，计算结果如表11 所示。

表11 不同供应商中断数量下制造商的总成本与弹性策略选择

表11 显示了供应商中断数量对制造商总成本和策略选择的影响，这也进一步说明了在突发事件引起的供应中断中，采取备用供应商和临时采购策略对减少供应链中断具有重要的作用。随着未中断供应商数量的减少和短期中断供应商或长期中断供应商数量的增加，制造商需要承担的总成本呈上升趋势。在未中断供应商数量相同的情况下，长期中断供应商的数量越多，制造商需要承担的总成本就越高；当供应商全部中断时，随着长期中断供应商数量的增多，制造商需要承担的总成本也会越多。同时，当未中断供应商的数量不超过全部供应商的一半时，制造商更倾向于选择备用供应商而不是临时购买策略。这是因为临时购买的成本高于备用供应商的采购成本，这从侧面反映出备用供应商通常比临时购买更具成本效益。当未中断的供应商数量超过全部供应商的一半时，在未中断的供应商数量相同的情况下，若存在两个以上的长期中断供应商，制造商更倾向于选择备用供应商和临时采购的组合策略。为验证求解方法的优越性，本文还计算了每个算例的求解时间（表11）。Gurobi 求解器的平均求解时间为0.006s，初步说明使用Gurobi 求解器求解本文提出的混合整数线性规划模型具有可行性。

为进一步验证直接使用Gurobi 求解本文提出的数学模型的优越性，对Gurobi 求解结果与使用python PULP 库求解的结果进行对比，分别记录两种方法求解5 组算例的目标函数值和求解时间，具体结果如表12 所示。

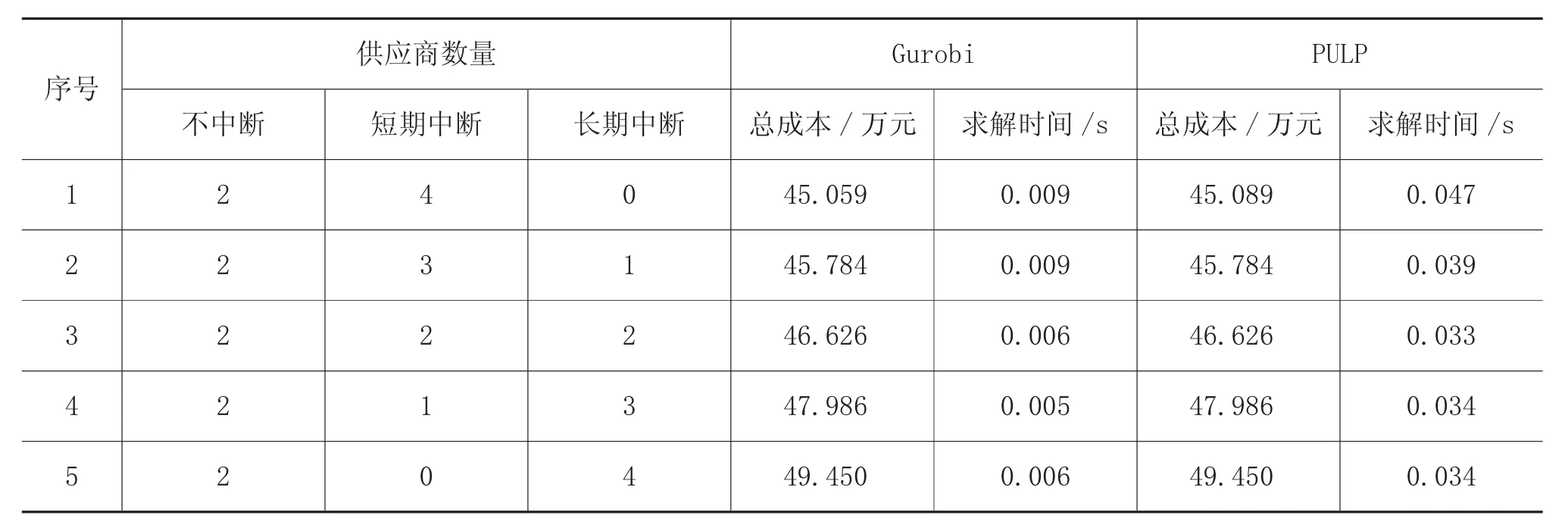
表12 两种求解方法的结果对比

从表12 可以看出，后4 组算例的最优值是相同的。在第1 组算例中，与PULP 库的求解结果相比，Gurobi 求解器得到的最优值更小。此外，Gurobi 求解器的求解时间均小于PULP 库的求解时间。这些结果表明，Gurobi 求解器具有较好的求解精度和求解速度。因此，Gurobi 求解器在求解本文提出的混合整数线性规划模型方面更具有优越性。

四、结 论

本文针对供应商、整车制造商组成的二级汽车供应链，研究了在突发事件影响下的供应中断问题。在中断发生时考虑了备用供应商和临时购买两种策略，并考虑供应商在突发事件影响下不发生中断、发生短期中断和长期中断3 种情况，建立了两阶段混合整数线性规划模型，目标是制造商的总成本最小化。通过算例分析模拟现实中断情况，验证了模型和策略的可行性和有用性。分析结果表明：（1）采用备用供应商和临时购买策略能够有效降低制造商的总成本。不论是采取单一策略还是组合策略，制造商需承担的总成本都明显低于不采取策略时产生的成本。（2）制造商的总成本随关键参数的变化而变化，且两者的变化趋势是一致的。其中，制造商总成本对备用供应商的单位采购成本的敏感度最高。（3）随着未中断供应商数量的减少以及短期中断供应商或长期中断供应商数量的增加，制造商需要承担的总成本逐渐上升。同时，供应商的中断情况影响弹性策略的选择。此外，计算结果表明使用Gurobi 求解器求解模型具有可行性。相较于现有关于供应链中断的文献仅考虑节点中断和需求不确定等问题，本文的创新之处在于在建立混合整数线性规划模型时，将供应商不中断、短期中断、长期中断3种状态融入数学模型中，兼顾了突发事件影响下供应商的状态对制造商策略选择和总成本的影响。同时，本研究通过使用启发式算法和分支界定法求解混合整数线性规划模型，提供了更高效和精确的求解方法，并揭示了供应商在不同状态下的最优采购方案和最优组合策略。因此，可以将提出的策略和模型应用到实际问题中，为决策者应对突发事件引起的供应中断问题提供一些启示。

本研究仅考虑了以供应商和制造商组成的两级汽车供应链，在后续的研究中可以考虑供应商、运输中转站以及制造商组成的三级供应链模型。突发事件引起的供应中断问题通常会伴随着运输中断的发生，今后研究可以将运输中断纳入模型中，设计更能体现实际问题的弹性供应链模型，为决策者在实际环境中应对突发事件造成的供应中断管理问题提供有价值的见解。