基于支持向量机的建筑工程混凝土质量可靠性分析

侍莘莘 （合肥热电集团有限公司，安徽 合肥 230031）

0 引言

混凝土质量检测是建筑工程检测过程中的重要一环，应当予以充分的技术支持。但是，在实际的混凝土质量检测过程中会受到很多因素的影响，例如环境因素、人为因素等，这些因素都有可能会对混凝土质量检测造成一定程度的影响[1-3]。因此，混凝土质量检测十分重要，所以针对如何提升质量检测的准确性有以下三点重要意义。一是混凝土质量检测可以对混凝土的质量进行精准的、全面的检查，同时又可以通过全面地分析得到准确的数据，从而为工作人员更精准地进行混凝土配比提供依据；二是通过混凝土质量检测可以进一步控制工程成本，由于将配比进行优化之后，减少了材料的浪费，进而降低了成本投入；三是混凝土质量检测可以提高建筑工程的安全性能，减少事故的发生，对于保障工程的安全也具有重大意义。

现阶段已经形成了有关混凝土的相关标准和使用规范，首先是因为混凝土是否达标直接关系到整个工程的持久性和安全性[4-6]；其次是因为建筑工程是较为普遍的，形成一套完整、系统的标准也有利于未来混凝土的配比；最后是一套标准可以有效地降低成本，减少不必要的浪费。在具体应用中，混凝土的质量也是衡量工程质量是否达标的重要指标。越来越多的学者意识到了混凝土的重要性，因此展开了更加深入的研究。同时，为提升国内的建造水平并和国际接轨，更要加强研究。随着时代的发展以及技术的不断更新，人工智能的使用范围逐渐变大，在混凝土配比的领域中也有所涉及。因此，人工智能技术在混凝土配比作业中建立的混凝土性能模型要比优化算法建立的模型更加精准、成本低且性价比更高，可以更精细化地完成配比工作。

1 项目概况

项目总建筑面积约为200516.10 m2，其中地上部分为157891.18m2，地下部分为46544.86m2。工程地面上主要由5栋高层住宅，2栋商业组成。8#楼西单元、9#楼东单元为34 层高层住宅楼，建筑高度为109.45m；8#楼东单元、9#楼西单元为27层高层住宅楼，建筑高度为96.70m；10#楼、11#楼为17 层住宅楼，建筑高度为56.70m；12#楼东单元为23 层住宅楼，建筑高度为79.30m，西单元为24 层住宅楼，建筑高度为82.20m；13#楼、14#楼为4层商业楼，建筑高度为23.00～25.20m。地下为两层，层高为3.60m，防水等级一级，耐火等级一级，抗震设防烈度为6 度，结构安全等级二级，地基基础设计等级甲级。此项目工程所需要的混凝土都是商品混凝土，并利用泵送设备进行施工。

2 混凝土的力学性能试验

2.1 混凝土制备

根据《普通混凝土力学性能试验方法标准》（GB/T 2558-2020）进行操作，依据抗压强度、抗折强度、劈裂强度测得的数据来评定混凝土的力学性能，再生混凝土性能的影响因素较多，根据混凝土配合比设计要求，混凝土力学性能影响因素主要包括水泥、粉煤灰、碎石、细骨料、减水剂、水量，这几种常用的组成材料的样本数据见表1。

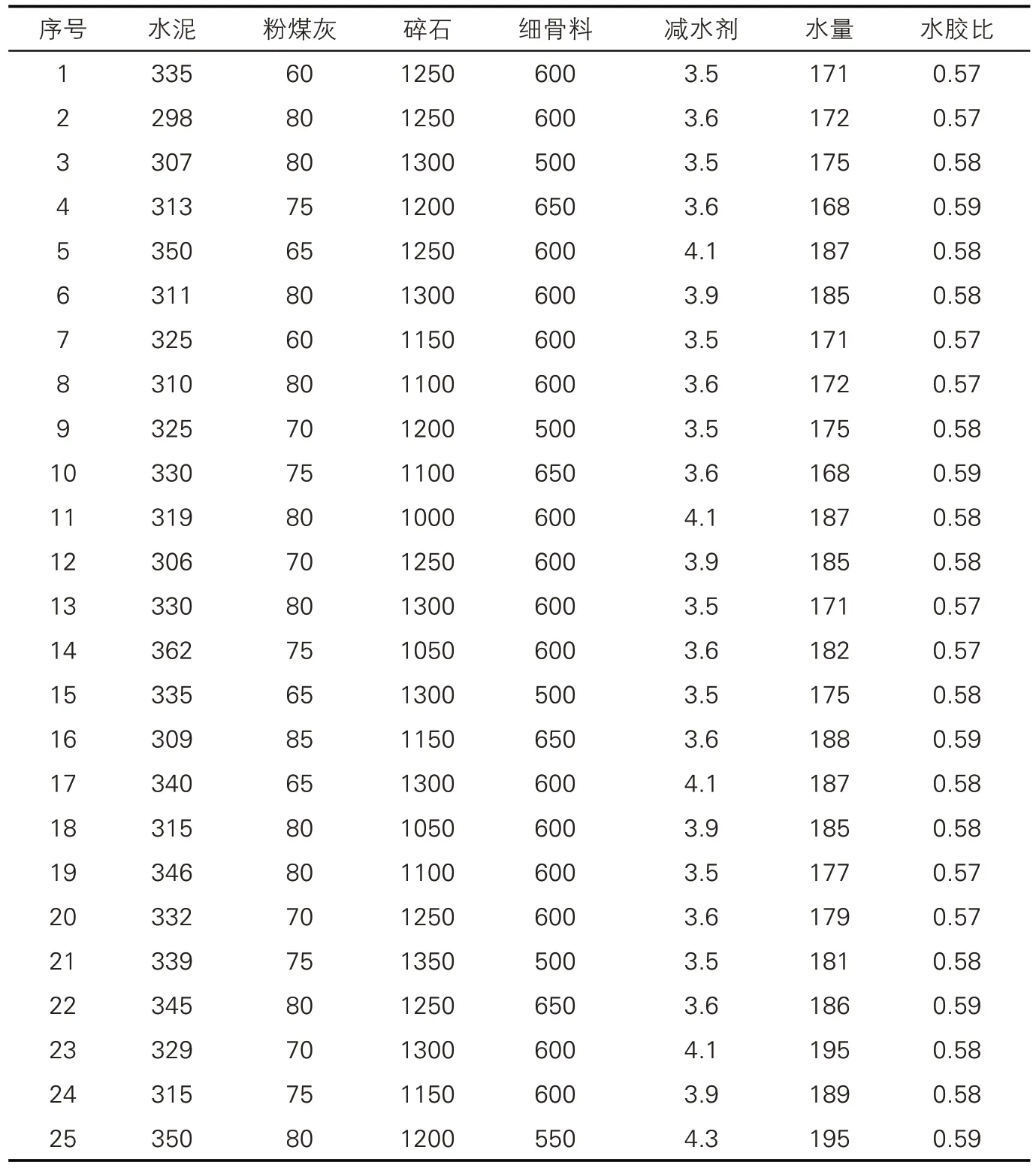
表1 组成材料的样本数据(单位：kg/m3)

将150mm×150mm×150mm 的立方体作为标准试块，把已经配比好的混凝土装到里面，并计算25L 的混凝土需要的材料量。在完成所有的材料称重之后，按照标准依次投放进搅拌机，在完成搅拌作业之后将其倒出，最后形成模具。试验主要设备见图1，试验主要过程见图2。先进行坍塌度的测试，然后再次将其倒进试模当中进行下一步工作，并在适宜的环境中进行保存。传统的混凝土配比需要进行多次，才能试验出适合施工的配比，这也就意味着需要耗费大量的人力、物力，造成浪费[7-8]。

图1 试验主要设备

图2 试验主要过程

2.2 实验结果

抗压强度试验结果如图3 所示，最大值为46.7MPa、最小值为38.9MPa；坍落度试验结果如图4 所示，最大值为19.6mm、最小值为18.1mm。根据水泥、粉煤灰、碎石、细骨料、减水剂、水量几个参数的配比，发现水泥与碎石的数值对抗压强度的影响最为明显，其次是粉煤灰与细骨料。

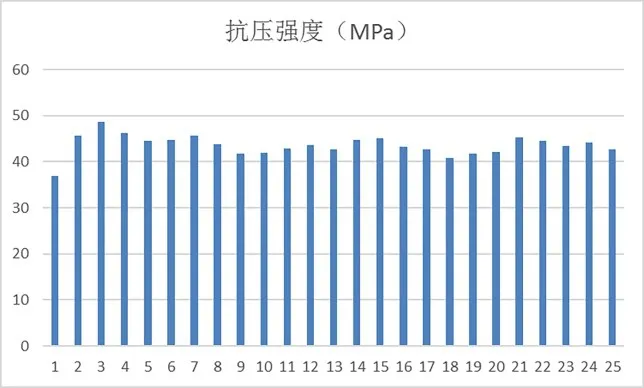
图3 抗压强度试验结果

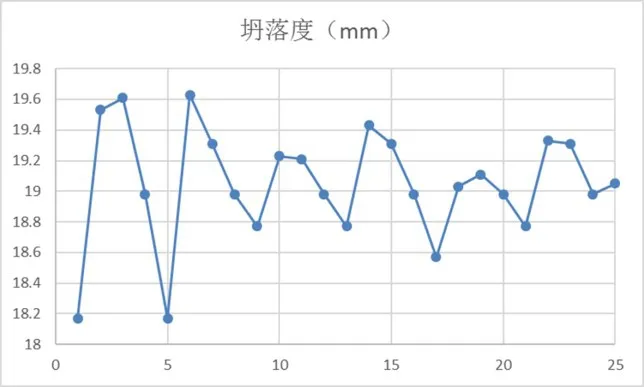
图4 坍落度试验结果

3 支持向量机的理论基础

3.1 支持向量机的原理

支持向量机（SVM）是基于应用统计学习理论的学习算法，处理小样本数据分类和相关的回归问题[9-10]。它主要是通过建立一个最优分类超平面，将输入空间中的不可分样本（无论是线性或者是非线性的样本）分开，如图5所示。

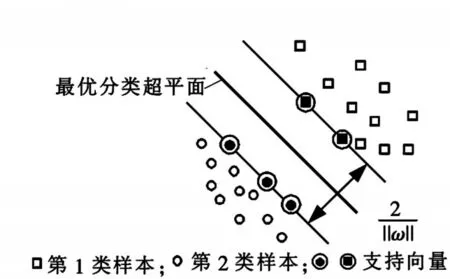
图5 最优分类超平面

最优分类超平面公式：

式中：w为权重；b为偏差。

原样本空间就可以分为两类样本，其公式表示为：

式中：yi∈[-1,1]，为输入参数。

但样本可能存在误差，为了校正存在的偏差，可以引入松弛变量εi和惩罚因子C，进而超平面的约束表示为：

Lagrangian 乘子为参数αi，转换为对偶问题，即：

根据Kuhn-Tucker 条件，αi必须满足αi[yi(wφ(xi)+b) - 1 +εi= 0]，当αi≠0 时，样本为支持向量。最后得到最优分类函数：

式中：m为支持向量的个数；K(x,xi)=φT(x)为核函数。

3.2 支持向量机核函数的选择

在支持向量机分类中，核函数的选择非常重要。核函数的主要功能是对样本数据通过相关的处理进行分类。本文选择的核函数为径向基函数（RBF），此核函数计算速度快、训练简单。

式中：u、v分别为数据集的两个样本；γ是核函数的系数。

3.3 支持向量机的基本流程

支持向量机的基本流程如图6 所示。

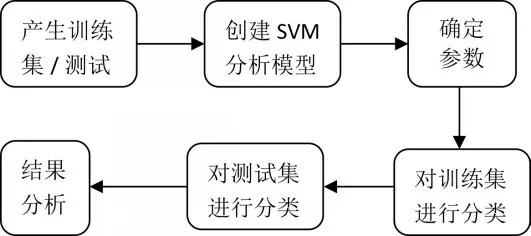
图6 基本流程

支持向量机的步骤如下：确定混凝土分析模型的输入和输出向量，并针对样本数据的特性及实际需求，将样本分为训练集和测试集；创建支持向量混凝土质量分析模型，得到相应的分类模型，在同一工况条件下确定模型参数；利用训练好的分类模型，对待测试的样本进行测试；结果分析。

4 基于支持向量机的建筑工程混凝土质量可靠性预测

混凝土的制作过程中，影响其运行安全性的因素众多，经过综合考虑选取对混凝土质量比较重要的性能参数（即水泥、粉煤灰、碎石、细骨料、减水剂、水量）作为输入量，输出量选择抗压强度与坍落度。在MATLAB 工具箱，利用改进的网格搜索法对SVM 惩罚参数C、核函数参数γ 寻优，这样可以减小寻优所花费的时间。参数的寻优范围为（2-15，215），经过优化选择后最终得到SVM 最优惩罚参数C=24.5634、γ=0.22067，寻优准确率为96.0387%。利用支持向量机的建筑工程混凝土预测模型，通过对10组样本进行训练，对另外的15组数据进行测试，为了保证训练样本的收敛，对其进行归一化处理。本次对样本数据中16～25 号样本进行训练，对1～15 号样本进行预测和验证。预测模型结果与试验值对比结果如图7、图8所示。通过对比支持向量机与试验结果绝对误差数据，最大误差没有超过5%，误差相对较小，准确率较高，模型相对稳定，算法更简洁、方便、实用。

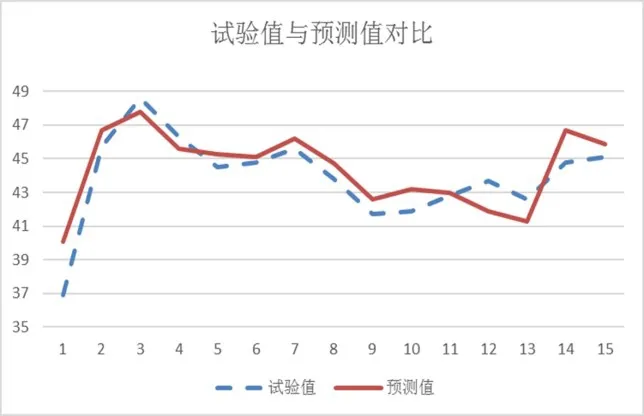
图7 抗压强度预测模型结果与试验值对比

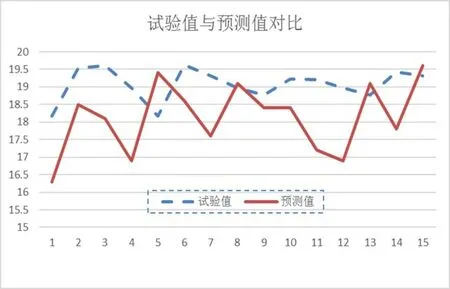
图8 坍落度预测模型结果与试验值对比

5 结论

具有良好的力学性能以及耐久性是优质混凝土的重要性能，也是未来混凝土改良的方向。在实际的工程施工中，混凝土质量能否符合施工标准是极其重要的。现阶段测量已经投入生产的高性能混凝土的强度成本较高，所以成本低且精准地测量出其强度是非常有必要的。本文通过支持向量机对试验测得样本数据进行混凝土的质量可靠性训练、验证和测试，预测正确率能达到95%。