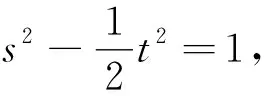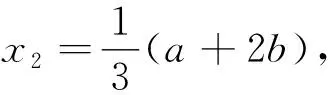巧借特殊值,妙解高考题
庄凤兰
福建省惠安第三中学 (362100)
在高考中,针对选择题可以利用特殊化进行合理寻觅或巧妙排除,确定满足条件的选项或结论,再回归一般性规律,得以正确判断或求解.特殊值法比较适用于高考中的一些函数、方程、不等式、数列等选择题,本文结合近年高考数学试题中一些客观题加以剖析.
例1 已知参数方程t∈[-1,1],以下哪个图象符合该方程( ).
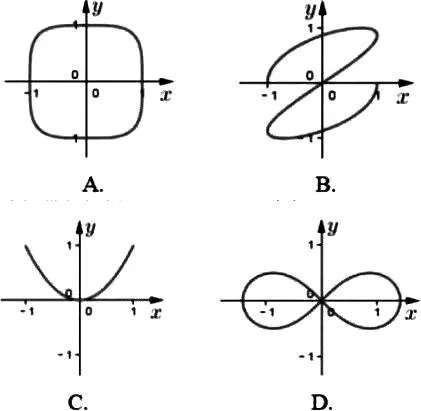
分析:结合题目条件中的参数方程,利用参数t在取值范围内的特殊值t=0与t=1的选取,进而确定对应变量的值,通过图象的特征加以合理排除,从而得以间接判断出满足条件的图象.
解析:巧取特殊值t=0,可得x=0,y=0,此时图象过坐标原点,由此可以排除选项A;又巧取特殊值t=1,可得x=-1,y=0,此时图象过x轴负半轴上的点(-1,0),由此可以排除选项C、D.故选B.
点评:合理利用特殊值巧判函数、方程等所对应的图象,利用满足条件的特殊值的有效选取,结合特殊点的确定与位置特征,与相应的图象加以对比分析,合理排除,巧妙判断.在利用特殊值巧判图象问题中,经常要多次利用特殊值的巧妙选取来合理排除,只剩下最后一个正确答案为止.
例2 (2021年上海卷第16题)已知x1、y1、x2、y2、x3、y3为6个不同的实数,满足①x1 A.2x2 C.x22 分析:结合题目条件中的6个不同的实数所满足的关系,巧取特殊值满足条件②,并确定x1、x2、x3三个值,进而确定另外三个实数的值,满足三个条件即可,在此基础上代入对应的选项来确定不等式是否成立即可. 解析:根据题目条件,巧取特殊值x1+y1=x2+y2=x3+y3=9,且x1=1,x2=2,x3=4,可得y1=8,y2=7,y3=5,同时满足三个条件,根据x1=1,x2=2,x3=4,只有选项A中2x2 点评:合理利用特殊值巧比大小是破解参数值、函数值、代数式等的大小比较的选择题中经常用到的一类特殊化思想方法,在解答一些大小比较的客观题中有一定的用武之地,简单易操作,只是特殊值的选取有一定的技巧性和局限性. 例3 已知a,b∈R,ab>0,函数f(x)=ax2+b(x∈R).若f(s-t),f(s),f(s+t)成等比数列,则平面上点(s,t)的轨迹是( ). A.直线和圆 B.直线和椭圆 C.直线和双曲线 D.直线和抛物线 分析:根据题设条件巧取满足ab>0的特殊值a=b=1,简化二次函数解析式,方便利用等比数列的定义建立与转化相应的关系式,有效地进行逻辑推理,更加利于平面上点的轨迹的确定与判断. 点评:合理利用特殊值巧化函数、数列、平面向量等的关系,进一步简化相关要素之间的关系的建立与转化,便于寻找联系、代数运算、逻辑推理等,对于优化解题过程,提高解题效益等都是很有益处的. 例4 设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则( ). A.a 分析:利用三次函数进行求导处理,确定导函数及其导函数的零点,分别利用参数a取正负情况下特殊值的巧取来分类讨论,结合极大值点的条件确定两零点之间的大小关系,进而确定参数之间的大小关系,从而得以判断对应的不等关系式. 点评:合理利用特殊值巧解涉及众多知识的综合问题,往往是逻辑推理与巧取特殊值的合理渗透与综合应用.确定此类综合问题时,在推理或求解过程中,要正确理解并明确复杂式子的内涵,合理选取特殊值加以正确运算、推理与应用.细致的验证与特殊值的运算是解决问题的关键. 巧借特殊值法,适当简化繁杂的逻辑推理与代数运算过程,合理回避题目对应数学知识的直接应用,从特殊值角度,简单处理,降低知识层次,弱化知识难度,强化思想方法,简化解题过程,提升解题效益,节省宝贵时间.