基于生长观念的拓展学习的实践与思考*
——以“完全平方公式的拓展学习”为例
徐秀峰 许梅杰
江苏省苏州市吴江区苏州湾实验初级中学 (215200)
拓展学习是指在教育教学过程中,对学习内容、形式、方法等扩容增加和优化发展.近期,在区初中数学教学研讨活动中,笔者基于生长观念,展示了一节完全平方式的拓展学习课,受到听课老师的肯定.
一、生长观念下的价值判断
1.拓展新公式,对已有公式再认识.完全平方公式是初中代数运算的基础公式,在整式乘法、因式分解、分式运算、二次根式化简等代数变形中有着重要作用.但是七年级学生运用完全平方公式时,常发生如(a+b)2=a2+b2,(a-b)2=a2-b2,(a-b)2=a2-2ab-b2,(a-2b)2=a2-2ab+2b2等错误,其原因是重视公式记忆、忽视公式理解,重视公式应用、忽视探究经验等.本课拓展学习目的是在新情境中重温公式探究过程,进一步理解公式结构,积累代数学习经验.
2.运用新方法,对数学思想再渗透.完全平方式的验证方法,可以多项式乘多项式化简,也可以表示图形面积得到等式,像这样数形结合的验证方法,对后续代数学习有着深远影响.在验证新公式时,进一步生长验证方法,如将多项转化成二项,将高次转化为低次,将差的运算转化为和的运算等,再如通过复杂的分割方式理解若干项和的平方公式,从二维面积、三维体积到高维度计算,由此看来,对公式的拓展学习不光是知识的拓展,更是思想方法的拓展与巩固,如特殊到一般、数形结合、转化、整体、模型等思想贯穿整节课.
3.经历新过程,对数学素养再发展.对七年级学生而言,二项式平方的拓展学习是有一定难度的,随着项数和次数的增加,公式展开结果会更加复杂,二项式展开还是高中数学的学习内容,是不是超纲、超标了?其实不然,本课拓展学习的目的不是知识的拓展,而是以知识生长为载体,渗透数学思想方法,积累数学活动经验,能够探究自然现象或现实情境所蕴含的数学规律,经历数学“再发现”的过程[1].素养的发展应指向人的主动发展,通过构建新的问题情境,设计有趣的数学活动,引领学生主动参与,尝试解决,自主思考,培养积极的学习心理和情感.
二、价值判断下的学习活动
(一)乐思寻疑
1.回忆公式:(a+b)2=,
(a-b)2=.
2.验证公式;
3.思考:(1)如何将完全平方式进一步“生长”?
(2)怎么探究“生长”出的问题?
设计意图:进一步认识公式结构(首平方,尾平方,乘积两倍在中央),理解两种验证方法,如多项式乘多项式法则,面积法(图1,图2)等,对于两数差的平方还可以转化成两数和.通过回忆完全平方式的学习过程,为本课的拓展学习奠定知识和方法的基础.提出两个问题,引导学生自然联想,初步形成公式“生长”的路径(长高、长胖)和验证方法(数与形).
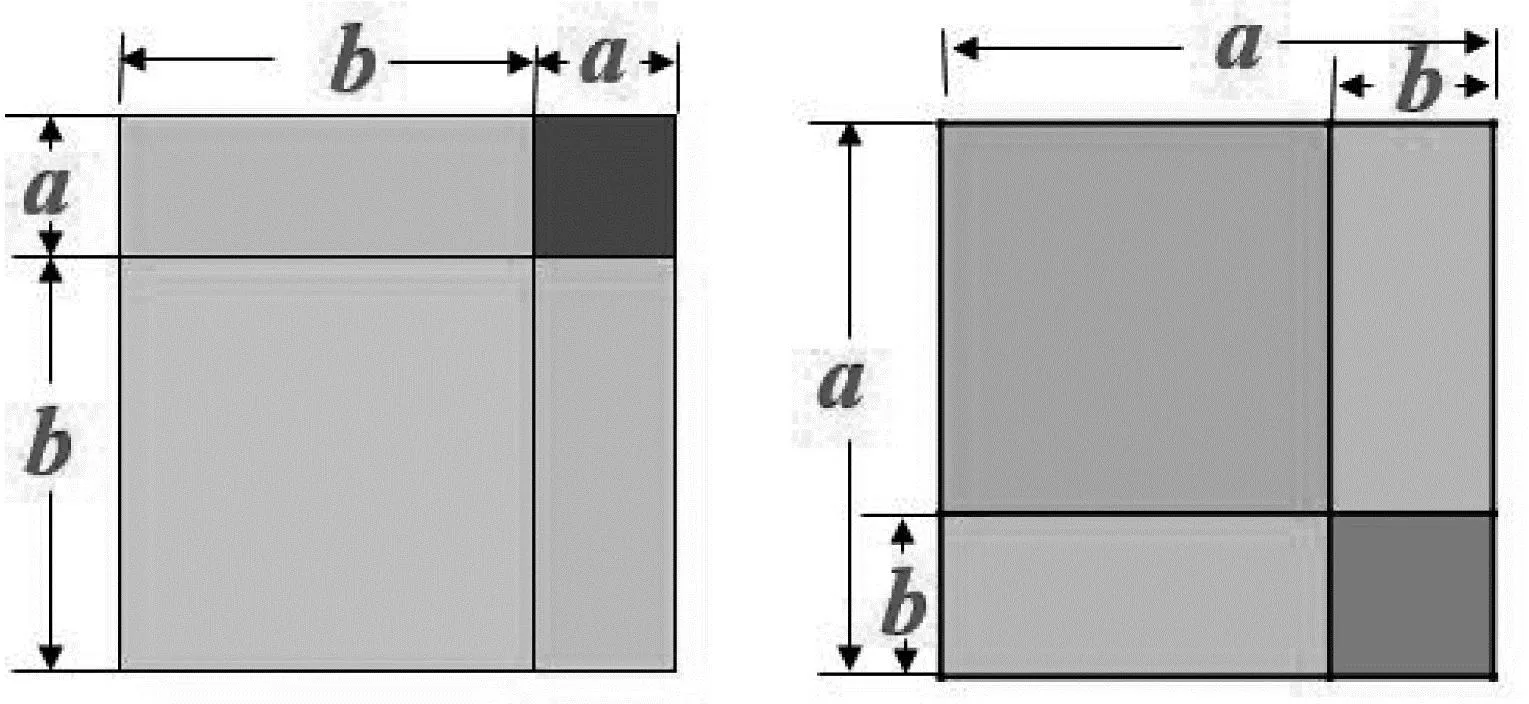
图1
(二)乐探解疑
1.生长方式1:增加项数
(1)探究:(1) (a+b+c)2;
(2) (a+b+c+d)2.
设计意图:遵循由简单到复杂,由特殊到一般的原则,从三项、四项和的平方开始,引导学生自主探究,可用多项式乘多项式,也可将三项或四项看成两部分,转化成两项和的平方(a+b+c)2=[(a+b) +c]2,(a+b+c+d)2=[(a+b)+ (c+d)]2,还可以可将正方形边长分成三部分或四部分,将大正方分割若干个小正方形(图3,图4),不同方式计算面积得到结果.观察计算结果,初步了解结构特征,猜想公式规律.
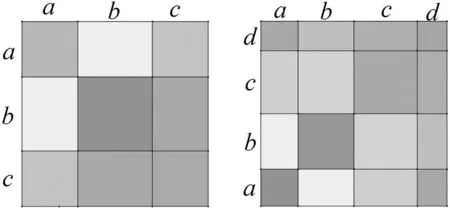
图3
(2)尝试:(a+b+c+d+e)2;
(3)推广:(x1+x2+x3+┈ +xn)2.
设计意图:从三项、四项发展到五项,先根据猜想说出结果,再用数与形两种方法进行验证,感受到面积验证的简便和直观.总结公式并推广到n项和的平方,尝试用数学符号表示,并类比两项和的平方表述,写出两项和的平方表述——若干个数的和的平方等于这些数的平方和与它们两两乘积2倍的和,结合图形感受公式的正确性.
(4)拓展:观察式子(图5),能提出什么问题?
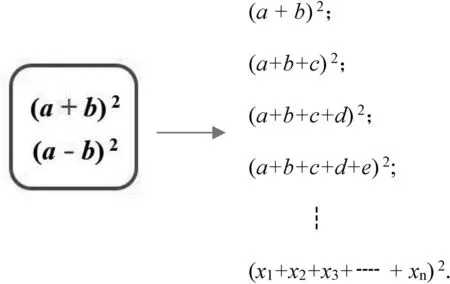
图5
探究:
设计意图:根据已有经验和探究结论(图5),生长出n项差平方的问题,并且类比两项差的平方研究方法,将差转化成和的形式,进一步完备公式形式(x1±x2±x3+┈ ±xn)2,渗透转化思想和整体思想.
2.生长方式2:增加指数
(1)探究:(1) (a+b)3;(2) (a+b)4.
设计意图:与探究增长项数的思路一致,从3次、4次开始探究,从数的角度,(a+b)3= (a+b)1· (a+b)2,(a+b)4= (a+b)2·(a+b)2,或者 (a+b)4=(a+b)1· (a+b)3等,从形的角度,(a+b)3可以看成棱长为(a+b) 的正方体体积,用不同方法表示体积得到等式(图6),对于(a+b)4有困难,由平方想面积是二维平面问题,由立方想体积是三维空间问题,那么四次方想什么,或者应该是四维空间问题,五次方、六次方┈也是如此,虽然不能借用图形理解,但留下丰富的遐想空间,促进学生的科学素养发展.

图6
(2)归纳:
① (a+b)2=a2+2ab+b2
② (a+b)3=a3+3a2b+3ab2+b3
③ (a+b)4=a4+4a3b+6a2b2+4ab3+b4
思考:运算结果有什么规律?
(3)尝试:(a+b)5=
设计意图:将已有结论整理,并逆生长出(a+b)1和(a+b)0,引导学生发现字母次数和系数的规律(图7),即一个字母升幂,另一个字母降幂,各项的次数不变,系数自上而下呈现三角形状,上下系数的联系等.根据规律尝试写出(a+b)5的结果,并用(a+b)5=(a+b)1· (a+b)4或(a+b)2· (a+b)3予以验证,进一步感受结论的正确性.

图7
(4)视频:(搜索“杨辉三角”进入百度百科,观看“秒懂百科”中“杨辉三角”的介绍视频.)
(5)推广:(a+b)n=
(6)观察式子,又能提出什么问题?怎样解决?
设计意图:引用网络资源,避免空洞说教,通过观看视频,了解杨辉三角的历史和意义,感受数学的神奇魅力,增强民族文化的自豪感.尝试用符号语言和文字语言叙述两项和n次方的规律,发展符号意识.在式子的对比过程中(图8),引导学生再次生长出两项差n次方的规律,并类比之前和差转化的方法,顺利解决问题,完备二项式展开规律(a±b)n,准确认识到代数变形的方法.
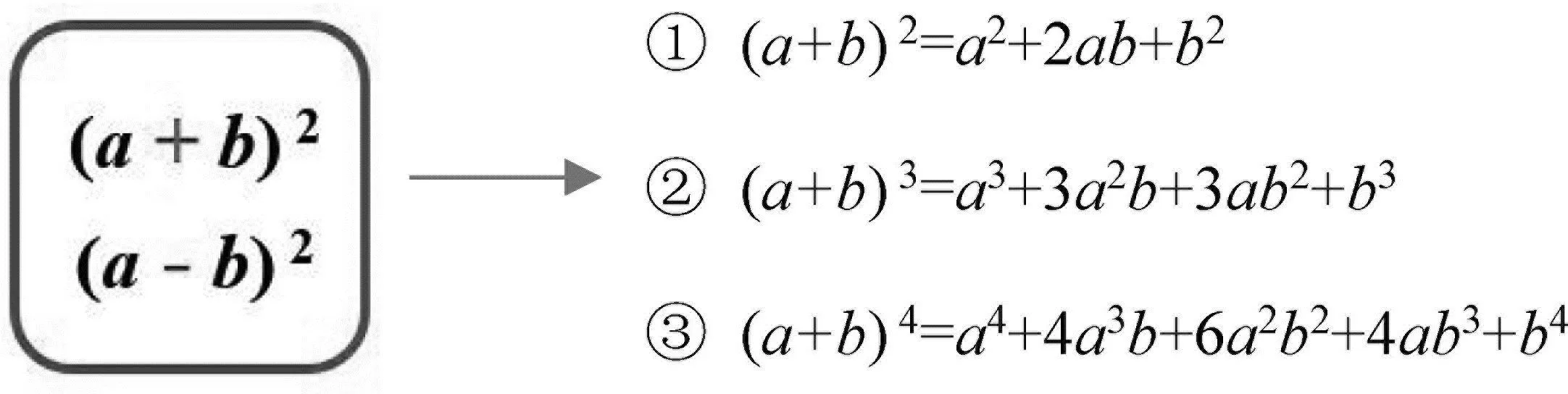
图8
(三)乐辨质疑
1.求值:(1)(x-y+1)2; (2) 114.
2.(a+b)10的展开式中所有项的系数和为.
设计意图:用拓展所得公式解决问题,体会公式的简单应用,增强学习新知识的兴趣.在二项式展开中进一步发现杨辉三角的神奇结论,激发继续探究的欲望,对中国古代数学文化的向往.
(四)乐构活疑
1.在拓展完全平方公式的过程中,了解到哪些新知识?
2.还能举出类似的知识“生长”例子吗?
设计意图:总结本课拓展学习的知识和方法,凸显知识生长过程、问题解决方法.回忆其他有关“生长”的例子,如从两个有理数的加法生长到多个数的加法、从两个同底数幂的乘法除法生长到多个同底数幂的乘法除法,从三角形的内角和生长到多边形内角和等,前后联系,一以贯之,为以后生长学习埋下种子.
三、学习活动后的深度思考
1.拓展学习是为促进学生个性化发展
“拓展”即开拓发展,是教材资源不够吗? 数学教材的意义不仅是教学内容的呈现,而是教学设计的蓝本、教学活动的资源、渗透思想的载体.每个学生都是鲜活生动的个体,不同学生的数学水平有差异,不同时期产生数学问题也不尽相同,如何满足学生的个性化需求,如何适应快速发展的社会,是新时代教师思考的重要问题.显然,统一的教材、单一的学习方式是不够的,比如对学有余力的学生而言,完全平方式不难掌握,但是仅通过二项式展开,学生很难体会公式结构中的“对称美”,探究方法中数与形的“统一美”,数学知识体系的“秩序美”,数学语言的“简洁美”等等,由此可见,对公式的拓展学习是有必要的.
2.拓展学习是为促进学生数学素养发展
一般地,拓展学习的目的不是拓展知识,更不提倡拓展超标、超纲的知识,应是以拓展知识为载体,促进能力和素养的发展(图9).如本课的学习目的不是掌握多项式平方展开式与二项高次方展开式,更不能以记忆公式、运用公式去解题为目的,而是让学生经历拓展学习的过程,即基于已有经验生长新问题、类比已有方法探究新公式、简单运用感悟新成果等.可能经过若干天之后,学生会忘记了拓展出的公式结构,也不会用新公式解决问题,但生长过程的体验,探究方法的巧妙,积极参与的情感会悄然影响学生品格.带给学生终身受用的哲学方法论上的认识,即让学生“带得走”的能力和素养[2],当把所有的教育都忘记了,剩下的就是素质!
图9
3.拓展学习需遵循生长观念
数学学习如树木生长一般,在已有知识上生长新知识,兼容并济,建构日益完备的知识体系;在已有能力上生长新能力,迭代升级,形成稳定全面的方法技能.拓展学习是常规生长之外的拔节生长,使枝更繁、叶更茂,是彰显个性的生长、是面向全面的生长.
(1)扩展学习建立在学生相对成熟的经验上,比如已经理解完全平方公式,并能运用公式解决问题了,引导学生发现新的生长点是基础,也就是如何突破已有经验和惯性思维.在新旧知识对比中发现已有知识的局限性,在解决新问题时发现已有知识不够或方法不行,依据数学发展规律学习时产生新的想法等,形成进一步生长的需要,激活拓展学习的种子.要给学生以自主探究的地位、独立思考的时空,形成过程的感受、体验成败的乐趣[3].
(2)拓展学习的难度有所提高,过程更有挑战性,产生持续生长力是关键.问题是生长的动力,用问题驱动扩展学习(本课问题设计如图10),激发探究欲望;情感是生长的润滑剂,用积极的人际关系营造心理氛围,体验成功收获快乐.无惧拓展学习难度,激发生长的主动性,从自觉生长到必然生长.
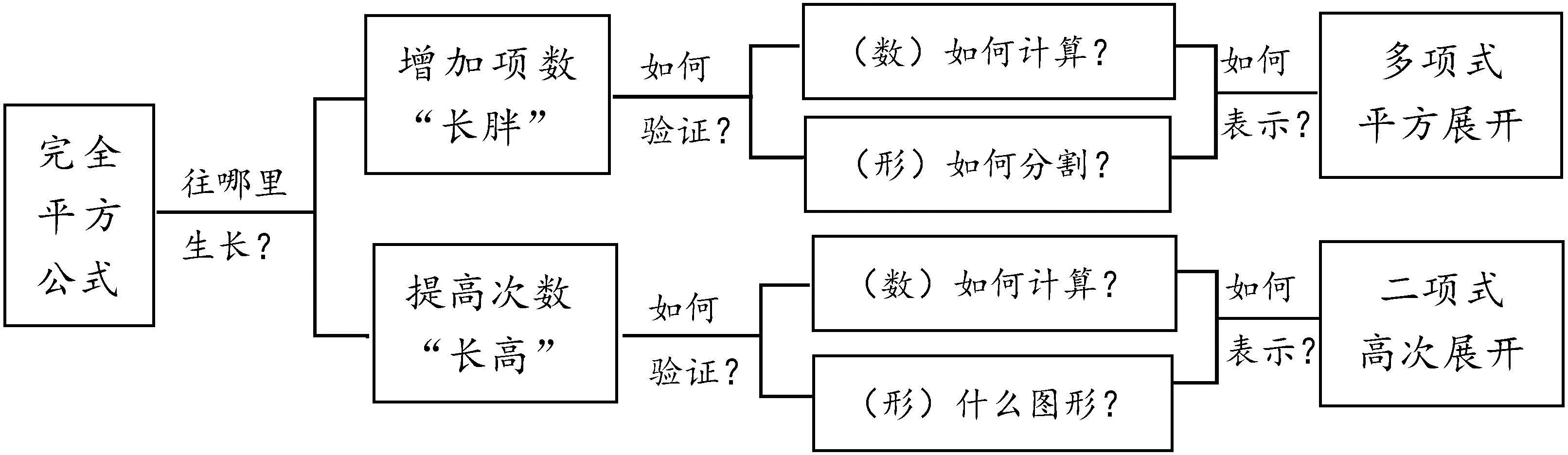
图10
(3)拓展学习的成果应指向素养的发展,渗透转化、数形结合、模型等数学思想方法,逐步充拓展学习的生长经验,激发生长的原生动力,形成“生长——再生长——生长”的拓展流程.拓展学习的成果应指向人的发展,促进学生可持续发展,培养良好的思维品质,坚定正确人生观和价值观,从数学生长走向人的生长.
四、结束语
拓展学习是常规学习的延伸,进一步优化学习方式,转变思维方式,有关数学拓展学习的资源建设、活动组织、评价机制等有待研究.拓展学习也是现代人必备的品质,敢于突破原有认知和能力,实现自我生长、自我突破!

